Вы думаете рисовать линии это просто?
- четверг, 2 мая 2024 г. в 00:00:15
Возьмите линейку, карандаш или ручку и начертите на бумаге линию. У вас выйдет как‑то так:

Вы скажете, что сложного в том, чтобы нарисовать линию? А теперь попробуйте нарисовать с помощью того же инструмента линию шириной в 5–10 раз больше ширины кегля. Уже сложнее не так ли?:

Ладно, скажете вы, у меня есть корректор, который гораздо толще ручки! Да, вы упростите себе задачу, но если нужно будет нарисовать линию толще? Будет снова не просто:

Вы придёте к выводу, что тонкая линия лишь кажется тонкой, если её приблизить, можно увидеть ширину и погрешность, что и при рисовании линии большей ширины. А всё дело в том, что линии это не геометрические объекты (т. е. не 1d объекты).
Все линии, которые мы можем создавать имеют толщину, а линии с толщиной это уже определённые плоскости (опустим тот факт, что в нашем мире всё имеет не нулевые размеры во всех трёх плоскостях). Но поскольку, чаще всего нам надо иметь однородную и симметричную линию, то линию можно спокойно представить как прямоугольник. А это значит, что задача нарисовать линию, сводится к задаче нарисовать прямоугольник.
В качестве визуализации процесса будем использовать OpenGL, а именно геометрические шейдеры на языке GLSL. Всё что они делают — это берут на вход точки фигуры, а далее строят из них фигуры. Весь их код будет прокомментирован, поэтому знания GLSL не обязательны для понимания процесса.
Для построения этого прямоугольника нам известны координаты центров его сторон, расположенных друг напротив друга. А так же ширина этих сторон. Найти же нам надо, координаты четырёх углов прямоугольника.

Так как прямоугольник симметричен, это значит что из координаты одного из углов можно будет достаточно просто выразить координаты остальных углов.
Точки P0 и P2 очень похожи на Ц0 и Ц1, однако имеют смещения по осям. Поэтому их можно выразить напрямую через эти смещения и координаты точек Ц0 и Ц1:

Координаты же точек P1 и P2 получить ещё проще — через симметрию относительно Ц0 и Ц1:

В результате нам надо найти лишь смещения x и y и через него можно будет получить координаты остальных точек. А сделать это можно как минимум двумя разными способами. Первый — требует минимальных знаний геометрии, второй — знаний работы с векторами. Какой из них проще для понимания решать вам, поэтому опишу их оба.
Начнём с метода, для которого нужны только знания теоремы Пифагора. В чём суть данного метода. Мы можем получить расстояние до точки P0 двумя разными способами, а из этого получить два уравнения, решив которые, мы получим её координаты. Вычтя из них координаты точки Ц0, мы и получим данное смещение.
Для начала нарисуем рисунок:

Нас интересуют две прямые L и M. Их длину через исходные данные можно получить вот так:
Или через интересующею нас точку вот так:
Два уравнения, две переменных значит, решение точно есть. Осталось лишь его найти. Для строгости, приведу полной этап их решения, тем более он тривиален. Раскроем скобки:
И ещё одни:
Заметим, что можно выразить квадрат длины расстояния между исходными точками:
В итоге получим:
А благодаря этому можно немного упростить выражение:
Теперь мы можем приравнять обе части:
Уберём повторы, и объединим одинаковые переменные, заодно и знаки поменяем:
Выразим x и y через друг-друга:
Подставим в исходное уравнение:
Приведём к нулю:
Решим его, для x:
Аналогично, для y:
Их тоже можно упростить, для этого раскроем скобки:
Заметим, что корень из квадрата это модуль, а делитель это расстояние между исходными точками:
В целом, так как у каждого выражения есть два решения, отличных только по знаку,а S и L всегда положительные, модуль можно и убрать:
В итоге, мы получили два уравнения, остаётся лишь вопрос, какое из двух решений каждого уравнения соответствует нашему сдвигу относительно изначальных точек.
Для этого рассмотрим четыре положения прямоугольника‑линии в пространстве, относительно центра. Так как точки симметричны, что было показано ранее, покажем влияние лишь на точку P0 :

Так как на знак, влияет лишь разница между координатами исходных точек, то проанализируем их знаки во всех возможных положениях точки P0:

Как можно заметить из таблицы, смещение для y в точности советует знаку разницы координат, значит уравнение для смещение y будет иметь положительный знак для точки P0 (а для точки P1 в силу симметрии отрицательный знак).
Для x ситуация ровно обратная, знак смещения всегда иной, чем знак разницы, значит уравнение смещения x будет с отрицательным знаком для точки P0 (а для точки P1 в силу симметрии положительный знак).
В итоге окончательно получим смещение:
Следующий метод приведёт нас к такому же результату, но совсем другим путём...
Точки на плоскости можно представить как вектора, характеризующийся величиной (длина вектора) и направлением от начала координат. Тогда, пусть точки P0 ,Ц0 и Ц1 это вектора P0‑,Ц0‑ и Ц1‑ направленные от начала координат.
Этот метод основан на том, что P0‑ и Ц0‑ ортогональны (т. е. между ними угол 90 градусов). Значит, мы можем повернуть вектор полученный из разницы векторов Ц0‑ и Ц1‑ на 90 градусов, и получить вектор Ц2‑ , такой же длины как расстояние от Ц0‑ до Ц1‑. А так же мы знаем расстоянии от P0‑ до Ц0‑ . Поэтому для определения вектора P0‑ достаточно найти соотношения длин векторов, и умножить на него координаты Ц2‑ . А уже через координаты P0‑ найти смещение.
Для начала найдём вектор разницы Ц0‑ и Ц1‑:

Для полученного вектора Ц2‑ используем формулы поворота вектора на угол на плоскости :
Подставим в формулу 90 градусов для того чтобы из ортогональному вектору P0‑ , получить сонаправленный вектор:
В итоге получим следующие определение координат точек:

Далее найдём соотношение длин вектора Ц2‑ и заданной ширины S:
Осталось только изменить длину вектора Ц2‑ , не меняя его направления, для этого умножим его координаты на соотношение длин:
Поставим на место К его уравнение:
Мы снова пришли к тем же формулам что и в прошлый раз!
И вот у нас есть всё необходимое для того чтобы нарисовать линию. Теперь визуализируем это, заодно собрав всё вместе. Для этого нам нужен конвейер рендера, который состоит из 6 этапов. Каждый из которых обрабатывает свои данные (подробнее в этом цикле статей) Из них мы можем влиять только на три этапа (выделены синим):

Для нашего случая вершинный шейдер просто перекладывает вершины, перемещая их в вершинный шейдер. Матрица модели нужна для позиционирования всей линии в пространстве(подробнее):
#version 330 core
//координаты точек линии
layout (location = 0) in float position_x;
layout (location = 1) in float position_y;
//матрица модели, задающая положения объекта в пространстве
uniform mat4 model;
void main(){
//передача позиции точек в геометрический шейдер
gl_Position = model *vec4(position_x,position_y,0.0f,1.0f);
}Фрагментный шейдер ещё проще, он задаёт один цвет всей линии:
#version 330 core
out vec4 color;
uniform vec4 mat_color;
void main(){
color=mat_color;//передаём цвет в растеризатор
};Любые 2d объекты могут быть представлены как группа треугольников (с некоторой погрешностью, конечно). Поэтому мы будем рисовать линию с помощью них. Геометрический шейдер получает две точки (сегмент линии) и на основе них строит прямоугольник из двух треугольников. Так как вывод из геометрического шейдера возможен только в виде triangle_strip (каждая вершина после второй создаёт новый треугольник), вершины будут представлены в таком порядке:

Сам код геометрического шейдера:
#version 400 core
layout (lines) in;//входные данные, две точки (x0;y0) и (x1;y1)
//входные данные, точки прямоугольника
//(прямоугольник рисуется с помощью двух треугольников,
//strip значит, что для построения второго треугольника
//будут использованны две вершины предыдущего)
layout (triangle_strip, max_vertices = 4) out;
in float S[];//передаём ширину линии
//Функция определения смещения
vec2 get_general_point_corner(vec2 P0,vec2 P1){
float L =(distance(P0,P1));
float K=S[0]/L;
float x_=-K*(P1.y-P0.y);
float y_=K*(P1.x-P0.x);
return vec2(x_,y_);
}
void bild_quard(vec2 A_0, vec2 P0, vec2 P1){
// 1:bottom-left
gl_Position =vec4((A_0.x+P0.x), (A_0.y+P0.y), 0.0, 1.0);
EmitVertex();
// 2:bottom-right
gl_Position =vec4((-A_0.x+P0.x), (-A_0.y+P0.y), 0.0, 1.0);
EmitVertex();
// 3:top-left
gl_Position =vec4((A_0.x+P1.x), (A_0.y+P1.y), 0.0, 1.0);
EmitVertex();
// 4:top-right
gl_Position =vec4((-A_0.x+P1.x), (-A_0.y+P1.y), 0.0, 1.0);
EmitVertex();
}
void main() {
//получаем смещения
vec2 p_= get_general_point_corner(gl_in[0].gl_Position.xy,gl_in[1].gl_Position.xy);
//строим прямоугольник-линию
bild_quard(p_,gl_in[0].gl_Position.xy,gl_in[1].gl_Position.xy);
EndPrimitive();
}
Если вы плохо знаете OpenGl, но хотите сами запустить этот пример, используйте информацию из этой статьи. (пример из неё очень просто адаптировать для данного случая). Если это вызовет проблемы, я дополню статью подробным методом (для строительства линии будем использовать каждую новую вершину для нового сегмента).
В итоге получим следующие:


С одной линией всё нормально, попробуем нарисовать кривую из разных линий:


Как мы видим, на стыке сегментов есть проблема — они не соединены, нужно отдельно реализовать соединение линий.В принципе можно выделить три типа соединений:
Косое
Прямое
Закруглённое
Для реализации каждого из них нам будет нужна информация о вершинах других сегментов. Для этого вместо layout (lines) in в шейдере используем layout (lines_adjacency) in, что даёт информацию об вершинах других сегментах.
В целом, мы можем просто соединить точки P2 и P4 следующим образом:

Для этого мы получаем в геометрическом шейдере смещение для другого прямоугольника, и находим через него точку P4. Можно было бы найти точно, с какой стороны нам рисовать треугольник для плавного стыка, на основе наклона двух линий, но лучше нарисовать лишний треугольник, чем добавлять условие. Для этого найдём точку P5 , и нарисуем прямоугольник P2P4P3P5.
Разбиение на треугольники его вершин будет таким же:
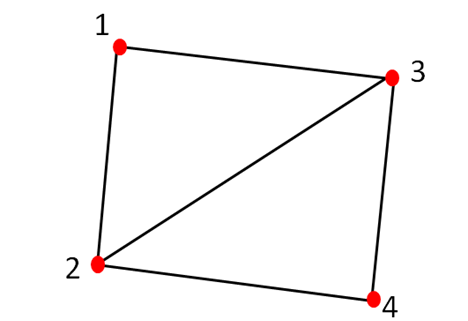
Код шейдера, на основе вышесказанного будет выглядеть вот так:
#version 400 core
//входные данные, четыре точки (x0;y0),(x1;y1),(x2;y2) и (x3;y4)
layout (lines_adjacency) in;
//входные данные, точки прямоугольника
//(прямоугольник рисуется с помощью двух треугольников,
//strip значит, что для построения второго треугольника
//будут использованны две вершины предыдущего)
layout (triangle_strip, max_vertices = 6) out;
in float S[];//передаём ширину линии
//Функция определения смешения
vec2 get_general_point_corner(vec2 P0,vec2 P1){
float L =(distance(P0,P1));
float K=S[0]/L;
float x_=-K*(P1.y-P0.y);
float y_=K*(P1.x-P0.x);
return vec2(x_,y_);
}
void bild_quard(vec2 A_0, vec2 P0, vec2 P1){
// 1:bottom-left
gl_Position =vec4((A_0.x+P0.x), (A_0.y+P0.y), 0.0, 1.0);
EmitVertex();
// 2:bottom-right
gl_Position =vec4((-A_0.x+P0.x), (-A_0.y+P0.y), 0.0, 1.0);
EmitVertex();
// 3:top-left
gl_Position =vec4((A_0.x+P1.x), (A_0.y+P1.y), 0.0, 1.0);
EmitVertex();
// 4:top-right
gl_Position =vec4((-A_0.x+P1.x), (-A_0.y+P1.y), 0.0, 1.0);
EmitVertex();
}
void oblique_connection(vec2 A_1, vec2 P1){
// верхний треугольник в стыке
gl_Position =vec4((A_1.x+P1.x), (A_1.y+P1.y), 0.0, 1.0);
EmitVertex();
// нижний треугольник в стыке
gl_Position =vec4((-A_1.x+P1.x), (-A_1.y+P1.y), 0.0, 1.0);
EmitVertex();
}
void main() {
//получаем смещения
vec2 p_= get_general_point_corner(gl_in[0].gl_Position.xy,gl_in[1].gl_Position.xy);
vec2 p_1=get_general_point_corner(gl_in[1].gl_Position.xy,gl_in[2].gl_Position.xy);
//строим прямоугольник-линию
bild_quard(p_,gl_in[0].gl_Position.xy,gl_in[1].gl_Position.xy);
//строим соединение стыка линий
oblique_connection(p_1,gl_in[1].gl_Position.xy);
EndPrimitive();
}
В итоге выйдет вот так:


Это самый эффективный способ по числу треугольников и описанию способ. Однако, возможны и иные решения этой проблемы.
Для этого типа разрешения стыка, нам необходимо определить точку P6 :

К счастью, сделать это очень просто, так как наши сегменты линии находятся на одной плоскости, то всегда можно найти точку пресечения двух прямых линий или сказать что они параллельны. А значит, для того чтобы найти эту точку, мы должны найти по точкам P0 и P2 первое уравнение прямой линии, и по точкам P4 и P5 второе уравнение, а потом их приравнять.
Для начала запишем уравнение прямой линии через две точки для P0 и P2 :
Перепишем его через смещения и координаты изначальных точек линии (т.е. центров), для этого просто раскроем переменные:
В итоге получается страшное уравнение:
Сократим лишние:
Раскроем скобки:
И ещё раз упростим:
Разделим его на три части:
Умножим первую и вторую часть на S/L :
Поменяем знаки в скобках:
И окончательно упростим:
Перепишем части уравнения ка отдельные константы:
Тогда уравнение примет вид:
Зачем мы это сделали?
Во‑первых, мы получили два константных компонента. Первый, c показывает смещение относительно центра координат до центра центральной линии(посмотрев на уравнение линии через две точки, мы увидим точно такую же константу, которая будет является единственной, и показывать смещение).
Во‑вторых, b показывает смещение от центральной линии прямоугольника до границ. Знак говорит о том, с какой стороны находится прямая линия заданная уравнением, слева(‑) или справа(+).
Далее, приравниваем уравнение:
И находим координату x (y можно будет найти через любое другое уравнение):
Как уже упоминалось в методе про косой скос, использовать условные выражения в шейдере может быть менее эффективно, чем добавление дополнительных треугольников. Поэтому мы найдём дополнительно точку пересечения через прямые линии проложенные через две других стороны прямоугольника. Благо, это просто изменение знака у переменной b на обратный, согласно второму факту.
Рисовать треугольники для этого стыка мы будем в таком порядке, из‑за требования каждая точка после второй — новый треугольник. И тут, в любом случае придётся строить дополнительные точки, даже если учитывать направление скоса, поэтому мы и будем строить его зеркально, располагая вершины вот так:

Я думаю код шейдера уже пояснять не нужно, тут тоже всё довольно просто. Из нового лишь функция, определяющая положение точки P6 (P9 ) :
#version 400 core
//входные данные, четыре точки (x0;y0),(x1;y1),(x2;y2) и (x3;y4)
layout (lines_adjacency) in;
//входные данные, точки прямоугольника
//(прямоугольник рисуется с помощью двух треугольников,
//strip значит, что для построения второго треугольника
//будут использованны две вершины предыдущего)
layout (triangle_strip, max_vertices = 6) out;
in float S[];//передаём ширину линии
//Функция определения смешения
vec2 get_general_point_corner(vec2 P0,vec2 P1){
float L =(distance(P0,P1));
float K=S[0]/L;
float x_=-K*(P1.y-P0.y);
float y_=K*(P1.x-P0.x);
return vec2(x_,y_);
}
void bild_quard(vec2 A_0, vec2 P0, vec2 P1){
// 1:bottom-left
gl_Position =vec4((A_0.x+P0.x), (A_0.y+P0.y), 0.0, 1.0);
EmitVertex();
// 2:bottom-right
gl_Position =vec4((-A_0.x+P0.x), (-A_0.y+P0.y), 0.0, 1.0);
EmitVertex();
// 3:top-left
gl_Position =vec4((A_0.x+P1.x), (A_0.y+P1.y), 0.0, 1.0);
EmitVertex();
// 4:top-right
gl_Position =vec4((-A_0.x+P1.x), (-A_0.y+P1.y), 0.0, 1.0);
EmitVertex();
}
vec2 get_point_corner(int side,
vec2 A_0,vec2 P0,vec2 P1,
vec2 A_1,vec2 P2,vec2 P3){
float a_0= -A_0.x/A_0.y;
float a_1= -A_1.x/A_1.y;
float b_0 = side*(A_0.x*A_0.x+A_0.y*A_0.y)/A_0.y + (P1.x*P0.y-P0.x*P1.y)/(P1.x-P0.x);
float b_1 = side*(A_1.x*A_1.x+A_1.y*A_1.y)/A_1.y + (P3.x*P2.y-P2.x*P3.y)/(P3.x-P2.x);
float x=-(b_0-b_1)/(a_0-a_1);
float y=a_0*x+b_0;
return vec2(x,y);
}
void direct_connection(vec2 T_0, vec2 T_1,vec2 A_1, vec2 P1){
gl_Position =vec4(T_0.xy, 0.0, 1.0);
EmitVertex();
gl_Position =vec4(T_1.xy, 0.0, 1.0);
EmitVertex();
gl_Position =vec4((A_1.x+P1.x), (A_1.y+P1.y), 0.0, 1.0);
EmitVertex();
gl_Position =vec4((-A_1.x+P1.x), (-A_1.y+P1.y), 0.0, 1.0);
EmitVertex();
}
void main() {
//получаем смещения
vec2 p_= get_general_point_corner(gl_in[0].gl_Position.xy,gl_in[1].gl_Position.xy);
vec2 p_1=get_general_point_corner(gl_in[1].gl_Position.xy,gl_in[2].gl_Position.xy);
//ищём точку угла
vec2 t_= get_point_corner( 1,p_,gl_in[0].gl_Position.xy,gl_in[1].gl_Position.xy,
p_1,gl_in[1].gl_Position.xy,gl_in[2].gl_Position.xy);
vec2 t_1=get_point_corner(-1,p_,gl_in[0].gl_Position.xy,gl_in[1].gl_Position.xy,
p_1,gl_in[1].gl_Position.xy,gl_in[2].gl_Position.xy);
//строим прямоугольник-линию
bild_quard(p_,gl_in[0].gl_Position.xy,gl_in[1].gl_Position.xy);
//строим соединение стыка линий
direct_connection(t_,t_1,p_1,gl_in[1].gl_Position.xy);
EndPrimitive();
}
В итоге на экране мы увидим:


Уже лучше, чем прошлый метод, и вполне хороший результат. Но можно поступить ещё интереснее, и сделать закругление линии.
В предыдущем методе мы определили точки для прямого стыка. А в методе косого стыка, мы использовали точки на разных линиях для создания косой линии. В этом методе нам понадобится все три точки для использования квадратной кривой Безье (подробнее в прекрасной статье). Этот метод является промежуточной между обоими стыками способом.

Чтобы нарисовать данную кривую нам понадобится её уравнение:
где t в диапазоне 0 до 1.
Достаточно менять t с определённым шагом, который и определит точность изгиба (чем больше шаг, тем меньше точность). Тут так же надо будет отзеркалить точки, для удобного рисования точек:

Как можно заметить, чтобы нарисовать такой парный изгиб, достаточно по‑очереди добавлять точки из обоих линий. На этом и основан шейдер для рендера этого случая:.
#version 400 core
//входные данные, четыре точки (x0;y0),(x1;y1),(x2;y2) и (x3;y4)
layout (lines_adjacency) in;
//входные данные, точки прямоугольника
//(прямоугольник рисуется с помощью двух треугольников,
//strip значит, что для построения второго треугольника
//будут использованны две вершины предыдущего)
layout (triangle_strip, max_vertices = 48) out;
in float S[];//передаём ширину линии
//Функция определения смешения
vec2 get_general_point_corner(vec2 P0,vec2 P1){
float L =(distance(P0,P1));
float K=S[0]/L;
float x_=-K*(P1.y-P0.y);
float y_=K*(P1.x-P0.x);
return vec2(x_,y_);
}
void bild_quard(vec2 A_0, vec2 P0, vec2 P1){
// 1:bottom-left
gl_Position =vec4((A_0.x+P0.x), (A_0.y+P0.y), 0.0, 1.0);
EmitVertex();
// 2:bottom-right
gl_Position =vec4((-A_0.x+P0.x), (-A_0.y+P0.y), 0.0, 1.0);
EmitVertex();
// 3:top-left
gl_Position =vec4((A_0.x+P1.x), (A_0.y+P1.y), 0.0, 1.0);
EmitVertex();
// 4:top-right
gl_Position =vec4((-A_0.x+P1.x), (-A_0.y+P1.y), 0.0, 1.0);
EmitVertex();
}
vec2 get_point_corner(int side,
vec2 A_0,vec2 P0,vec2 P1,
vec2 A_1,vec2 P2,vec2 P3){
float a_0= -A_0.x/A_0.y;
float a_1= -A_1.x/A_1.y;
float b_0 = side*(A_0.x*A_0.x+A_0.y*A_0.y)/A_0.y + (P1.x*P0.y-P0.x*P1.y)/(P1.x-P0.x);
float b_1 = side*(A_1.x*A_1.x+A_1.y*A_1.y)/A_1.y + (P3.x*P2.y-P2.x*P3.y)/(P3.x-P2.x);
float x=-(b_0-b_1)/(a_0-a_1);
float y=a_0*x+b_0;
return vec2(x,y);
}
void bezier_connection(vec2 T_0, vec2 T_1,vec2 A_0,vec2 A_1, vec2 P1){
vec2 H0=vec2( A_0.x+P1.x, A_0.y+P1.y);
vec2 H1=vec2(-A_0.x+P1.x,-A_0.y+P1.y);
vec2 H2=vec2( A_1.x+P1.x, A_1.y+P1.y);
vec2 H3=vec2(-A_1.x+P1.x,-A_1.y+P1.y);
float t=0.0;
int count=16;
for(int z = 0; z < count+1; z++){
vec2 B_0=(1-t)*(1-t)*H0+2*t*(1-t)*T_0+t*t*H2;
vec2 B_1=(1-t)*(1-t)*H1+2*t*(1-t)*T_1+t*t*H3;
gl_Position =vec4(B_0.xy, 0.0, 1.0);
EmitVertex();
gl_Position =vec4(B_1.xy, 0.0, 1.0);
EmitVertex();
t+=1.0/count;
}
}
void main() {
//получаем смещения
vec2 p_= get_general_point_corner(gl_in[0].gl_Position.xy,gl_in[1].gl_Position.xy);
vec2 p_1=get_general_point_corner(gl_in[1].gl_Position.xy,gl_in[2].gl_Position.xy);
//ищём точку угла
vec2 t_= get_point_corner( 1,p_,gl_in[0].gl_Position.xy,gl_in[1].gl_Position.xy,
p_1,gl_in[1].gl_Position.xy,gl_in[2].gl_Position.xy);
vec2 t_1=get_point_corner(-1,p_,gl_in[0].gl_Position.xy,gl_in[1].gl_Position.xy,
p_1,gl_in[1].gl_Position.xy,gl_in[2].gl_Position.xy);
//строим прямоугольник-линию
bild_quard(p_,gl_in[0].gl_Position.xy,gl_in[1].gl_Position.xy);
//строим соединение cтыка линий
bezier_connection(t_,t_1,p_,p_1,gl_in[1].gl_Position.xy);
EndPrimitive();
}И в итоге получим:
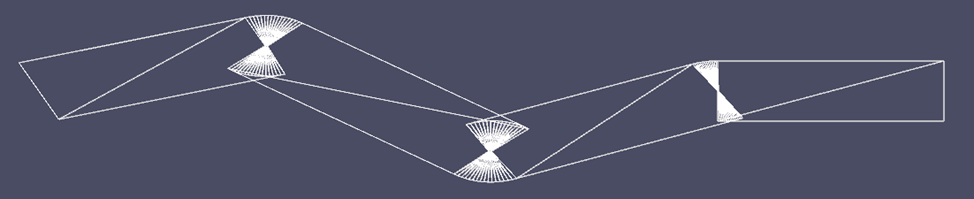

Как можно заметить, каждый следующий метод стыка, использует также промежуточные расчёты предыдущего, что наглядно показывает почему был выбран именно этот порядок описания методов.
В нашей жизни есть много вещей, которые на первый взгляд кажутся простыми, например, линия. Но если присмотреться, то всё становится гораздо интереснее. Даже чтобы провести простую линию, чуть толще, чем инструмент, нам нужно вспомнить основы геометрии.
Отвечая на вопрос, поставленный в заголовке статьи, можно сказать, что рисовать линии просто, если они тонкие, и сложно, если глаз видит различия.