Введение в нейросети: что, зачем и как?
- воскресенье, 7 апреля 2024 г. в 00:00:12
В сети полно примеров программного кода нейронных сетей, однако подавляющее большинство составлено с использованием дополнительных библиотек и «математических приёмчиков» — не вдаваясь при этом в какие‑либо подробности — мол, работает шайтан — и уже хорошо, главное — что «уместилось» в N строчек кода и «объяснено» всего за M минут.
Не берусь утверждать, что нейросети — это «элементарная база», но всё же попытаюсь максимально упростить эту тему; по возможности, не утрачивая информативность.
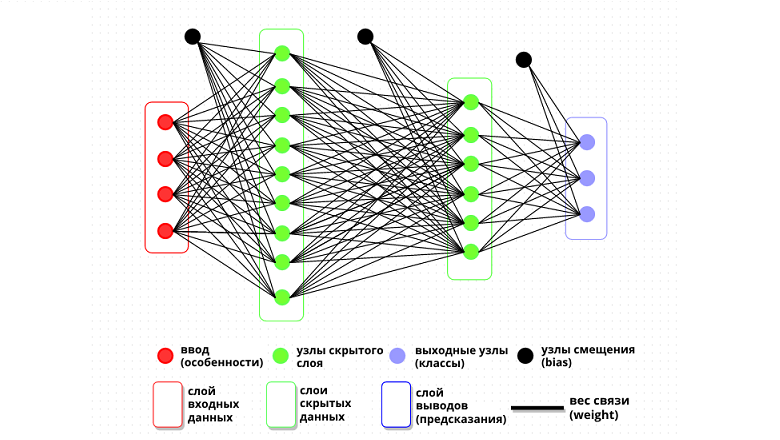
«Нейрон» — биологическое название нервной клетки; биологическая «нейронная сеть» — нервная система. Искусственная нейронная сеть — это реляционная база данных, в которой коэффициенты реляций — они же «веса связей», между данными в ячейках — они же «узлы» — заведомо неизвестны и генерируются псевдо‑случайным образом — этот процесс называется инициализацией нейросети. Такая нейросеть (инициализированная) со случайными коэффициентами «весов связей» на практике бесполезна и является «необученной». Чтобы «обучить» нейросеть выдавать более‑менее точные и, следовательно, полезные расчёты — необходимо дать ей заведомо точные результаты расчётов и программу «машинного обучения», которую в данном контексте можно считать искусственным интеллектом — хотя на деле, если докопаться до деталей — эта программа не намного «интеллектуальнее» пресловутого программного сортировщика или генератора псевдослучайных чисел.
Программа машинного обучения генерирует случайное число (инициализация) из указанного диапазона (обычно от -0.5 до +0.5) в качестве коэффициента - он же "вес"; затем входные данные умножаются на этот коэффициент, а все такие произведения для каждого отдельно взятого узла - суммируются (прямое распространение). Эта сумма произведений далее "причёсывается" так называемой "функцией активации", чтобы умещаться в конечный диапазон (обычно от 0 до 1) - в качестве такой функции чаще всего используется "сигмоида" - подробнее о ней напишу чуть ниже. Вывод из функции активации сравнивается с требуемым результатом (функция потерь) - в зависимости от результата сравнения корректируется значение "веса" для следующей итерации (обратное распространение) - и эта рекурсия может повторяться до бесконечности, с каждым шагом потенциально сужая диапазон вероятных значений. То, на сколько этот диапазон уменьшился относительно начального диапазона - отражает текущий показатель точности прогнозов нейросети; например, если из диапазона "0 - 1" остался диапазон "0.87 - 0.88", то такая нейросеть достигла уверенности (точности прогнозов) - 99%.
Замена данных во входном слое обученной нейросети на новые данные (для прямого распространения) - позволяет классифицировать эти данные с помощью этой нейросети.
Обладая обученной нейросетью, выдающей достаточно точные прогнозы - можно пропускать через эту нейросеть (через эту реляционную базу данных) уже другие данные, которых не было в учебном датасете (dataset - коллекция данных) - где нам заведомо неизвестен правильный расчёт, но исходя из похожести новых данных на данные из обучающей выборки и исходя из точности подобранных на учебной выборке "параметров" мы можем обладать некоторой уверенностью в том, что рассчитанный такой нейросетью прогноз по своей точности практически не уступит точности прогнозов в учебном датасете.
Эта уверенность - равняется произведению двух коэффициентов: первый - это точность прогнозов нейросети на учебном датасете, и второй - это похожесть новых данных на данные из учебного сета. Например, если нейросеть обучалась на картинках кошек и собак и достигла 99% точности в опознании тех и других, но если новые данные для такой нейросети не будут похожи ни на собак ни на кошек, а будут даны, к примеру, бобёр и синица - то нейросеть, конечно же, скажет, кто из них больше похож на собаку, а кто на кошку, но не более того - такая нейросеть никогда не даст разумного ответа о данных, сильно отличающихся от всего на чём она училась.
По сути - выходит, что нейросети - это инструмент классификации и автоматизации прогнозов, применимый к относительно стабильным системам - это такие системы, которые либо практически не меняются со временем (меняются значительно медленнее, чем нейросеть обучается), либо меняются циклично - что позволяет создавать учебные датасеты в очень высокой степени похожие на реальные данные, с которыми в будущем будет работать нейросеть. Например - анатомию тела можно считать стабильной системой: она может не меняться тысячелетиями. Это позволяет калибровать нейросети на датасетах людей с различными недугами, обучая их ставить не менее точные диагнозы, чем самые квалифицированные медики. И обратный пример: спортивные матчи, фондовый рынок, траектории элементарных частиц - нестабильные, хаотичные системы, где предсказания даже самой прокаченной нейросети, как и любого человека-эксперта - могут нести только развлекательный характер. Не то что бы всё это было совсем бесполезно - нет; среднерыночную прибыль, сопоставимую с банковским вкладом, можно с высокой долей вероятности "поднять" на бирже, если строго придерживаться инвестиционных советов ботов - просто их показатели не какие-то выдающиеся, а очень даже средние, если не сказать минимальные - ведь в конечном счёте, финансовые боты позиционируются именно как инструмент сбора и анализа огромных объёмов данных, на основе которых они всего лишь вычисляют показатель риска и составляют чарты по наименее рискованным инвестициям - но не прогнозируют прибыль вкладов и, конечно же, не гарантируют её. Да - если сравнивать "игру вслепую" со стратегией искусственного интеллекта - само собой, стратегия будет (в среднем) более выгодна - но эта выгода будет минимальна - меньше чем, например, темпы роста биткоина - но и с меньшими рисками. Именно поэтому многие инвесторы были шокированы внезапной закупкой Илоном Маском криптовалюты на полтора миллиарда американских долларов, но что с того? Миллиардер не прогадал и заработал на этом; его акции поднялись больше, чем акции тех, кто придерживается стратегии BlackRock - получается, его рискованный прогноз оказался прибыльнее общего "расчётливого тренда" - и это лишь один пример из бесчисленного множества.
Прямое распространение - это преобразование входных данных (особенностей) в сигналы на выходе (классы или прогнозы). Прямое распространение применяет к данным (умножает) текущие (подобранные в процессе обучения) коэффициенты связей (параметры), суммирует такие вводы для каждого узла и пропускает полученный результат через фильтр - через функцию активации.
Прямое распространение влияет на значения узлов (нейронов).
Функция активации - по сути просто аппроксимация; применяется в тех случаях, где ответ должен укладываться в конечный диапазон - когда значения ведущих к ответу узлов, помноженных на коэффициенты связей, в этот диапазон не укладываются и вообще могут быть изначально никак не ограничены. Подобное "сжатие" диапазона ответов называется функцией активации, которые бывают разные, например "сигмоида" -
Примечание: тот же символ (сигма) - часто используется для формулы среднеквадратичного отклонения, которая очень похожа на среднеквадратичную ошибку, о которой пойдёт речь чуть ниже - но всё же, они разные: в среднеквадратичной ошибке нет операции извлечения квадратного корня.
Каждый узел выходного слоя можно обусловить как какой-то произвольный класс - после чего итеративно (пошагово) модифицировать параметры нейросети таким образом, чтобы поступающие в неё данные, проходя через эту нейросеть, разрешались в один из этих классов - подобно тому как у людей различные визуальные образы ассоциируются с различными смыслами.
Если прямое распространение выглядит довольно прозрачно - умножение, сложение и аппроксимация, то обратное распространение - процесс вычисления "неверных" связей - может показаться чуть менее очевидным.
Обратное распространение - это процесс коррекции параметров; его же можно воспринимать как процесс обучения. Начинается с функции потерь и продолжается математическим инструментом "производная", вытекающим в "цепное правило".
Обратное распространение влияет на значения коэффициентов связей (весов).
Смысл "обратного распространения ошибки" - в том, чтобы максимизировать вывод на "правильных" узлах - соответствующих корректным классам, и минимизировать ошибку - выводы на всех остальных выходных узлах.
Первый шаг в обратном распространении - расчёт влияния так называемой "стоимости ошибки" (на математическом языке - функция потерь) из последнего слоя - слоя вывода, на коэффициенты связей (параметры), ведущие к этому слою.
На математическом языке, композитную (сложную) функцию от функции потерь для каждого выходного узла искусственной нейросети можно сформулировать следующим образом (если выглядит страшно, то, наверное, можно её пока пропустить):
Эта же формула, но записанная по-другому (я не издеваюсь, вдруг так правда проще?):
где z - сложная функция (прямого распространения) от всех параметров нейросети и функции потерь для выходного узла n; f - функция потерь; σ - функция активации (на примере сигмоиды); k - количество скрытых слоёв нейросети; i - количество узлов в слое; n - номер выходного класса.
Объединив все переменные в общую композитную функцию прямого распространения по нейросети - с помощью правил дифференцирования, можно определить индивидуальный вклад в функцию от каждой переменной - что, в свою очередь, необходимо для коррекции (обучения) параметров искусственной нейросети в ходе обратного распространения ошибки.
Но перед, непосредственно, "обратным распространением" - необходима небольшая ремарка об упомянутой выше функции потерь.
Существуют разные функции потерь - для разных ситуаций и для продвинутых пользователей, но в большинстве случаев можно обойтись функцией среднеквадратичной ошибки (Mean Squared Error): MSE возводит в квадрат разность полученного результата и ожидаемого (эталонного), затем суммирует все такие квадраты разностей между собой и делит на количество этих квадратов. MSE удобна своей универсальностью, поскольку не важно что из чего вычитать - умножение результата самого на себя (возведение в чётную степень) всегда будет давать положительный результат:
Вообще говоря - для обучения искусственной нейросети, сам показатель не важен - значение имеет лишь его динамика.
В математике уже давно изобретён (или открыт?) инструмент для исследования динамики функций - и называется он "производная". Произво́дная функции - понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Применимо к искусственным нейросетям это означает, что с помощью частной производной (и цепного правила) можно вычислить вклад каждой отдельно взятой нейронной связи в общую функцию потерь.
Объявим функцию потерь от двух переменных:
Тогда общая функция потерь будет выглядеть так:
где n - количество классов (выходных узлов) в нейросети.
Общая функция потерь на основе среднеквадратичной ошибки:
С помощью правил дифференцирования функции от нескольких переменных, находим частные производные (общей) функции потерь по прогнозам (они нужны для последующих вычислений), принимая все остальные слагаемые за постоянные (производная которых равна нулю):
Примечательно, что этот процесс дифференцирования делает равными между собой производные от общей функции потерь и от какой-либо отдельно взятой функции потерь по какой-то конкретной переменной:
К тому же, множитель (2/n) в данном случае, как и ноль, не играет никакой роли - всё равно дальше всё будет умножено на параметр "шага обучения", который задаётся произвольным образом.
В итоге - в контексте последнего слоя нейросети, частная производная функции потерь (общей или частной) по какому-то конкретному выводу выглядит так:
где i - номер (индекс) выходного узла (класса).
Эту формула напоминает игру "холодно-горячо", где она в буквальном смысле выдаёт значения температуры, только наоборот: при эталоне равном нулю, вычитание нуля из любого значения будет вытекать в положительные значения производной; а при эталоне равном единице - вычитание единицы из любого меньшего числа будет давать отрицательную производную функции потерь.
Положительную производную функции потерь по прогнозам - можно понимать как количество ошибки; а отрицательная производная функции потерь относительно прогнозов - указывает на степень правильности.
К сожалению, такая "обратная" логика не очень хорошо укладывается в общую картину нейросетей, где принято увеличивать значения "на верном пути" и уменьшать ошибку - поэтому полученный результат умножается на отрицательный коэффициент шага обучения - этот множитель определяет скорость обучения, задаётся вручную и его калибровка позволяет снизить количество эпох - итераций обучения, необходимых для достижения приемлемой уверенности в прогнозах.
Производная функции потерь по прогнозам, умноженная на (отрицательный) шаг обучения - это и есть самые первые параметры, рассчитанные в самом начале того, что уже называется "обратным распространением ошибки".
В переводе на человеческий язык, формула выше означает, что производная сложной (композитной) функции равна произведению производных - внешней функции и внутренней.
Примечание: в обозначениях Лейбница цепное правило для вычисления производной функции z = z(f), где f = f(x), принимает следующий вид:
Для дальнейших определений, введём понятие "взвешиваемого узла" - это следующий за каким-то конкретным весом (параметром) узел (нейрон). При прямом распространении, значения узлов умножаются на "исходящие" из них параметры - так вот, вес в контексте "взвешиваемого узла" - это именно "входящий", а не "исходящий" вес.
Применяя цепное правило относительно коэффициентов связей - можно вычислить частную производную общей функции потерь по весу связи "w" - градиент по параметру "w"
Частная производная общей функции потерь по какому-то весу "w" - равна производной общей функции потерь по выводу взвешиваемого этим весом узла, умноженной на производную вывода (взвешиваемого узла) по вводу (взвешиваемого узла), умноженной на производную ввода (взвешиваемого узла) по этому весу:
примечание: цифры в квадратных скобках перед выражением - означают его "уровень"; я добавил их для наглядности - далее по тексту будет ясно, зачем они. Математического смысла они не несут, в вычислениях не участвуют!
Рассмотрим по отдельности каждый множитель из этой формулы; начнём с первого - производная общей функции потерь по выводу узла "х".
Поскольку общая функция потерь является суммой всех функций потерь,
то это же верно и для её производной (одно из правил):
Перепишем это же уравнение по отношению к выводу какого-то узла "х":
где n - количество выходных классов; x - индекс взвешиваемого узла.
Каждое слагаемое из этой суммы можно найти по следующей формуле:
где i - целое число от 1 до n, где n - количество выходных узлов нейросети.
При прямом распространении, ввод узла "i" вычисляется простым умножением значения (вывода) узла "x" на коэффициент исходящей из него связи "w"(xi):
Следовательно - искомая в ходе обратного распространения производная ввода следующего слоя от вывода предыдущего - равна коэффициенту связи (весу) между взвешиваемым узлом и этим вводом:
Производная функции потерь по вводу - как сложная функция, раскладывается в произведение производных:
Ну а здесь уже всё "родное" - первый множитель вспомним из недавних расчётов:
По поводу второго множителя - поскольку вывод с какого-либо узла является функцией активации от его ввода,
то производная вывода по вводу - равняется производной от функции активации по этому вводу, применённой в ходе прямого распространения ко взвешиваемому узлу:
Подставим найденные значения в формулу "уровнем" выше:
И ещё выше - в итоге, получаем формулу производной частной функции потерь по выводу взвешиваемого узла:
В этой формуле примечательно использование веса w(xi), исходящего из взвешиваемого узла: именно поэтому данный метод коррекции называется "обратным распространением ошибки" - потому что первыми по порядку корректируются значения выходных параметров, а за ними - на их основе, корректируются более глубокие параметры - и так далее - с последнего слоя нейросети до первого.
Далее - подставляем всё это в формулу производной общей функции потерь по выводу какого-то узла "х":
где n - количество выходных узлов нейросети; w - параметр, исходящий из взвешиваемого узла.
Вернёмся к "главной" формуле:
Первый множитель - только что обозначенная сумма;
Производная вывода узла по его вводу - это производная от его функции активации:
Производная от ввода по весу - просто равняется предыдущему выводу, из которого идёт связь с искомым весом:
где p - индекс узла из которого идёт связь со взвешиваемым узлом; w(px) - входящая связь во взвешиваемый узел. Смещение (bias) - "голый" вес без коэффициента узла - важный элемент, без которого нейросеть работает менее точно, чем с ним. Ну правда - я не знаю как лучше его объяснить, да и зачем? Иногда лучше просто "shut up and calculate".
Итоговый вид формулы производной общей функции потерь по весу "w" до узла "x":
для узла "х" из последнего слоя:
для узла "х" из всех остальных слоёв:
где x - индекс взвешиваемого узла; p - индекс "исходящего" узла; n - количество выходных узлов в нейросети; х ∉ p ∉ n
Примечания:
если индекс p относится к "узлу смещения" (bias), то переменная "вывод(р)" упраздняется в единицу;
w(px) - вес связи от узла "p" до узла "x";
w(xi) - вес связи от узла "х" до узла "i".
Итак, нейросеть - это некоторое множество "вводов", на каждый из которых поступают данные из разных источников (подобно нервным окончаниям у людей) и связи различной силы этих "вводов" с "выводами", которые эта нейросеть делает из полученных данных. Что-то ещё?
Ну, во-первых - прямая связь "ввода" с "выводом" - это то, что называется одним "слоем" нейронной сети, а таких слоёв может быть множество - где "вывод" одного слоя - это "ввод" следующего. Если у нейронной сети больше одного слоя, то все "промежуточные" слои - называются "скрытыми" (hidden). Когда у нейросети более одного скрытого слоя - то такая сеть считается "глубокой" - от термина "глубокое обучение" (deep learning), посвящённого, собственно, обучению таких сетей. Смысл таких слоёв (и "глубокого обучения") в том, чтобы усложнить связи между вводом и выводом - добавить коэффициенты к коэффициентам, позволяющие более гибко адаптировать их значения под требуемые результаты.
С увеличением количества скрытых слоев и количества узлов в этих слоях увеличивается "выразительность" сети - её способность выделять зависимости и закономерности во входных данных. Однако с увеличением сложности сети, каждый следующий слой поднимает затраты на обучение такой сети - в геометрической прогрессии; кроме того - слишком "сложная" нейросеть - с избытком скрытых слоёв - будет страдать от "переобучения" - это когда нейросеть слишком хорошо "запоминает" обучающий датасет и утрачивает способность обобщать его с новыми данными. Поэтому - выбор оптимального количества скрытых слоев и количества узлов в этих слоях является важной задачей при проектировании нейросети и требует тщательного анализа и экспериментов.
Во-вторых - так называемые "нейроны смещения" - узлы с фиксированным значением - добавляются к каждому скрытому слою и не имеют "входных" связей: своеобразные усилители сигнала.
В-третьих - "функция активации" - по сути просто аппроксимация; применяется в тех случаях, где ответ должен укладываться в конечный диапазон. Например - функция активации ReLU
Ну и последнее - "функция потерь" - это первый градиент, с которого начинается обратное распространение.
Cписок всех логических элементов искусственной нейронной сети:
входные узлы (особенности)
коэффициенты связей (параметры)
узлы смещения (bias)
скрытые слои
функция активации
функция потерь
выходные узлы (прогнозы)
Всего-то 7 штук! И все известны уже более 30 лет.
Теперь - подробно разберём программный код нейросети на питоне - классификатора изображений, способного определять, на какую из десяти различных цифр больше всего похоже данное ему изображение.
Программа состоит из трёх частей: учебный датасет "MNIST" (который скачивается по этой ссылке), состоящий из 60 тысяч картинок цифр с названиями; программный модуль, преобразующий данные из этого датасета и, собственно, код самой нейросети. Сначала - код модуля get-mnist:
# модули numpy и pathlib должны быть установлены в питон
import numpy as np
import pathlib
# Объявление функции "get_mnist", которая будет возвращать значения, указанные ниже в команде return (images и labels).
def get_mnist():
# Из файла извлекается два массива: images (из ключа “x_train”) и labels (из ключа “y_train”). x_train содержит изображения цифр, а y_train - соответствующие им метки (цифры от 0 до 9).
# Примечание: предполагается, что файл mnist.npz размещён в папке data, которая находится в папке со скриптом.
with np.load(f"{pathlib.Path(__file__).parent.absolute()}/data/mnist.npz") as f:
images, labels = f["x_train"], f["y_train"]
# Преобразуем тип данных массива images в float32 и сожмём значения в диапазон от 0 до 1 путем деления на 255.
images = images.astype("float32") / 255
# images - трёхмерный массив двухмерных картинок, [0] измерение это количество картинок, а измерения [1] и [2] - размерности по высоте и ширине. Умножив размерности [1] и [2] друг на друга - получается общее количество пикселей в изображении. На выходе получается двухмерный массив - матрица.
images = np.reshape(images, (images.shape[0], images.shape[1] * images.shape[2]))
# Здесь метки преобразуются в формат "one-hot encoding". Мы создаем матрицу размером 10x10, где каждая строка представляет одну метку (цифру от 0 до 9). Значение 1 в строке соответствует метке, а остальные значения равны 0.
labels = np.eye(10)[labels]
# Функция возвращает два массива: images (обработанные изображения) и labels (one-hot encoded метки).
return images, labelsДалее - разберём код самой нейросети - программы машинного обучения:
# Ниже код программы машинного обучения искусственной нейросети - классификатора изображений
from data import get_mnist
import numpy as np
import matplotlib.pyplot as plt
"""
w = weights (вес), b = bias (смещение), i = input (ввод), h = hidden (скрытый), o = output (вывод), l = label (правильный ответ)
e.g. w_i_h = weights from input layer to hidden layer (вес_ввод_скрытый - вес связи между вводом и скрытым слоем)
"""
# Загрузка данных из датасета
images, labels = get_mnist()
# Инициализация весов случайными числами
w_i_h = np.random.uniform(-0.5, 0.5, (20, 784))
w_h_o = np.random.uniform(-0.5, 0.5, (10, 20))
# Инициализация смещений нулями
b_i_h = np.zeros((20, 1))
b_h_o = np.zeros((10, 1))
# learn_rate - шаг обучения, epochs - количество итераций, nr_correct - отслеживает количество правильных предсказаний
learn_rate = 0.2
nr_correct = 0
epochs = 3
# Цикл обучения
for epoch in range(epochs):
# Чтобы numpy мог посчитать скалярное произведение, необходимо подготовить одномерные матрицы img и l; использование zip ползволяет обрабатывать соответствующие элементы из нескольких массивов одновременно
for img, l in zip(images, labels):
img.shape += (1,)
l.shape += (1,)
# Прямое распространение ввод -> скрытый слой: вес смещения ввода суммируется с произведениями вводов и их весов (произведения между собой так же суммируются)
h_pre = b_i_h + w_i_h @ img
# Применение функции активации "сигмоида": np.exp - функция экспоненты - возведение числа Эйлера в степень, указанную в скобках. При возведении экспоненты в отрицательные степени - результат стремится к нулю, а при возведении в положительные - к бесконечности
h = 1 / (1 + np.exp(-h_pre))
# Прямое распространение скрытый слой -> вывод: вес смещения скрытого слоя суммируется с произведениями значений узлов скрытого слоя и их весов (произведения между собой так же суммируются)
o_pre = b_h_o + w_h_o @ h
# Применение функции активации "сигмоида"
o = 1 / (1 + np.exp(-o_pre))
# Стоимость ошибок, она же Функция потерь (на примере среднеквадратической ошибки; в данном коде эта переменная никак не используется и оставлена просто для наглядности)
# e = 1 / len(o) * np.sum((l - o) ** 2, axis=0)
# Если ячейка с максимальным значением в слое вывода совпадает с ячейкой с максимальным значением в одномерной матрице l - labels - то счётчик правильных ответов увеличивается
nr_correct += int(np.argmax(o) == np.argmax(l))
# Обратное распространение вывод -> скрытый слой (производная функции потерь)
delta_o = (2/len(o)) * (o - l)
# К весу от скрытого слоя до вывода (на каждый нейрон соответственно) добавляется произведение его правильности на шаг обучения: у ошибочных результатов показатель отрицательный и, следовательно, он вычитается.
# Транспонирование матриц - необходимо для их умножения. Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что матрицы согласованы.
w_h_o += -learn_rate * delta_o @ np.transpose(h)
b_h_o += -learn_rate * delta_o
# Обратное распространение скрытый слой -> ввод (производная композитной функции - производная функции активации умноженная на производную функции потерь))
delta_h = np.transpose(w_h_o) @ delta_o * (h * (1 - h))
w_i_h += -learn_rate * delta_h @ np.transpose(img)
b_i_h += -learn_rate * delta_h
# Показать точность прогнозов для текущей итерации обучения и сбросить счётчик правильных прогнозов
print(f"Уверенность: {round((nr_correct / images.shape[0]) * 100, 2)}%")
nr_correct = 0
# Показать результаты - запрашивает у пользователя номер картинки, которая будет пропущена через нейросеть прямым распространением, в результате которого нейросеть предскажет какая цифра на картинке
while True:
index = int(input("Введите число (0 - 59999): "))
img = images[index]
plt.imshow(img.reshape(28, 28), cmap="Greys")
# Прямое распространение ввод -> скрытый слой
h_pre = b_i_h + w_i_h @ img.reshape(784, 1)
# Активация сигмоида
h = 1 / (1 + np.exp(-h_pre))
# Прямое распространение скрытый слой -> вывод
o_pre = b_h_o + w_h_o @ h
# Активация сигмоида
o = 1 / (1 + np.exp(-o_pre))
# argmax возвращает порядковый номер самого большого элемента в массиве
plt.title(f"Нейросеть считает, что на картинке цифра {o.argmax()}")
plt.show()Этот пример, с классификацией цифр датасета MNIST - можно считать "hello world" задачей из мира нейросетей - достаточно наглядный и при этом не слишком сложный код. Если его понимание не вызвало трудностей и интерес к теме сохранился - то можно дополнить список функций активации (начинайте с ReLU - она самая популярная) - wikipedia
Окей, с тем как нейросети классифицируют объекты - разобрались: даются вводные данные, даются эталонные данные и случайным образом инициализированные параметры "подстраиваются" под эти данные - в процессе обратного распространения ошибки.
Этот же принцип - но применённый не к параметрам, а к узлам первого слоя - слоя ввода - "лёгким движением руки" превращает обученную нейросеть-классификатор в генератор новых данных (например, изображений):
Значения узлов вводного слоя изменяются на произвольные величины (в данные вводится шум или же данные полностью заменяются шумом) - эти изменения передаются прямым распространением по обученной нейросети до выводов, которые меняются в соответствии с изменениями ввода, а по динамике этих изменений нейросеть отслеживает - какие изменения и на каких узлах ввода лучше соответствуют требуемым выводам, а какие - хуже. Таким образом - за каждую итерацию "примеряя" к требуемым выводам небольшие произвольные изменения данных (например, цвета пикселей) - отбрасывая не подходящие значения и закрепляя подходящие - нейросеть за множество итераций формирует наиболее подходящий под запрошенные выводы результат, как бы "рассеивая" перекрывающий его шум:
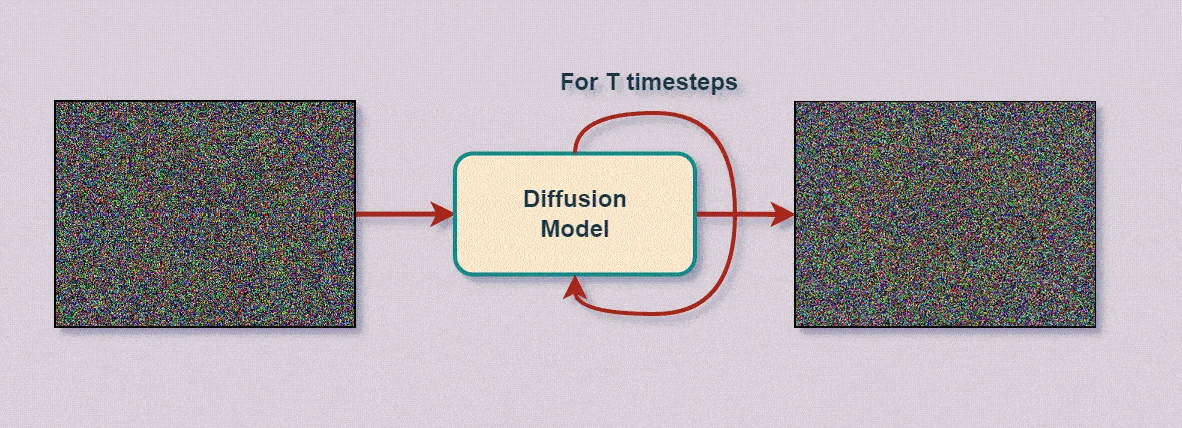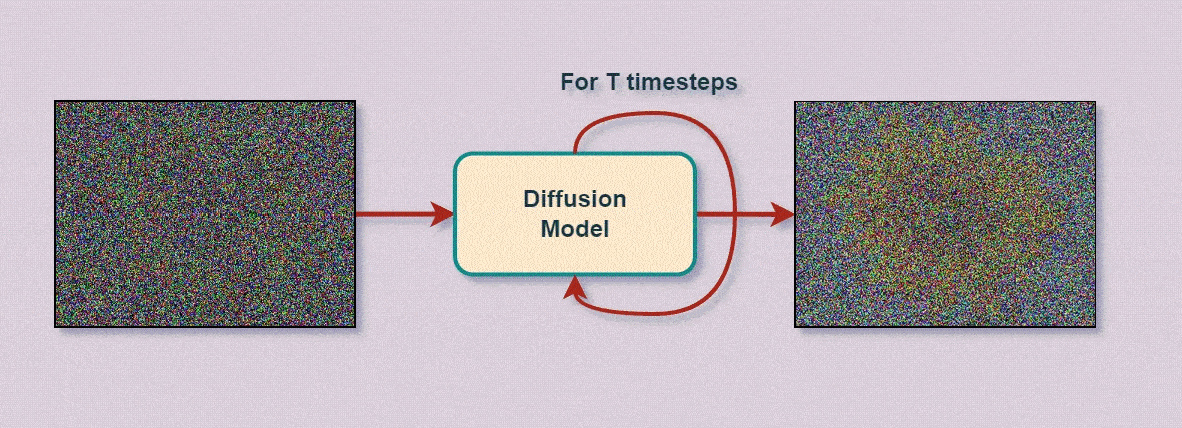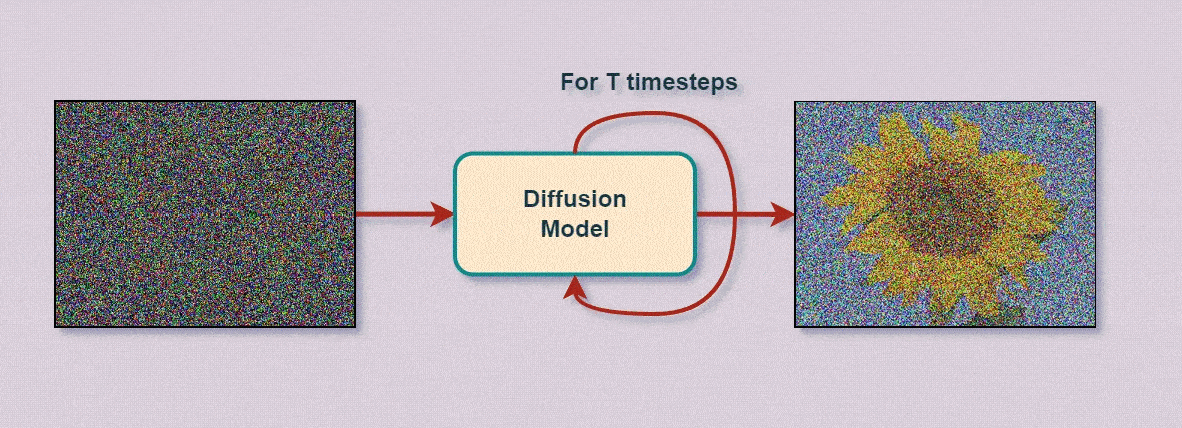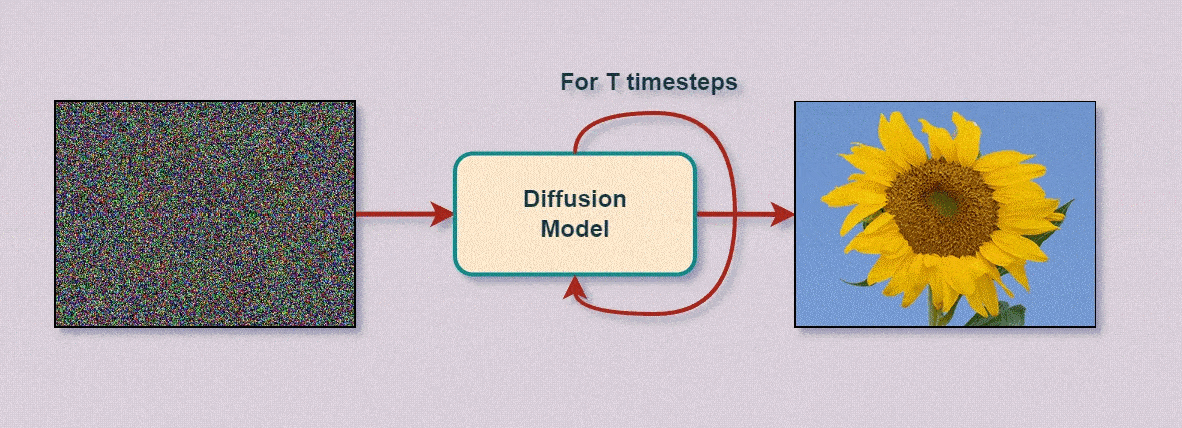
Например - у нас есть нейросеть-классификатор, обученная на различных изображениях, среди которых есть подсолнух. Показывая нейросети этот (или любой другой) подсолнух - мы вводим определённую последовательность данных (пиксели на входном слое нейросети), которые, проходя по всем узлам и параметрам, больше всего разрешаются в класс, соответствующий "подсолнуху". Само собой - на разные изображения "реакция" нейросети будет отличаться - условно говоря, относительно нейросети, всегда будут какие-то более "подсолнечные" подсолнухи, чем остальные, ничем не худшие - просто снятые с другого ракурса и расстояния.
Вводя в изображение подсолнуха минимальный шум - изменяя значения пикселей на случайные, но небольшие величины - будет меняться и уверенность нейросети в том, что перед ней всё ещё подсолнух. Постоянно добавляя к изображению шум, рано или поздно - исходное изображение станет совершенно неразличимым - изнутри нейросети это выглядит как наименьшая уверенность - наименьший вывод по всем классам.
Ну а теперь, "дело за малым" - взять да обратить процесс добавления шума примерно так же, как описанное выше обратное распространение обращает прямое.
Но ведь шум то - случайный! Обратить такое - уже не так просто, как обратить функцию по производной. Любой случайный шум - безвозвратно удаляет часть информации; удаление такого случайного шума либо восстановление информации - задача, по крайней мере до недавних пор, весьма нетривиальная. Для решения такой задачи необходим алгоритм, во-первых, отличающий "шум" от "не шум" и, во-вторых, алгоритм, заменяющий найденный им шум на данные, наиболее подходящие по контексту. Как бы к этой задаче подошёл человек? А давайте проверим - как же хорошо что перед монитором как раз есть такой!
Очевидно - что шума больше на правой. Очевидно, но почему? Чем мы можем характеризовать помехи? Давайте посмотрим на картинки поближе:
Если взять два увеличенных участка с этих картинок и сравнить между собой - будет ли так же очевидно, на каком из них больше шума, как это очевидно с исходниками? А вот и нет! В случае с увеличенными фрагментами - перед нами могут быть две примерно одинаково хаотичных картинки.
Выходит, что шум - это что-то вроде меры хаоса в системе и получается, что эта мера напрямую зависит от масштабов этой системы: в масштабах увеличенных фрагментов 10х10 пикселей мера хаоса оказывается выше, чем в их исходниках значительно большего размера. Почему? Как ни банально - просто потому, что больший масштаб всегда содержит в себе больше смысловых элементов, чем меньший. Именно с общего плана мы видим, что слева - перед нами горы, камни, вода, небо, а справа - люди и воздушные шары. И лишь поняв это, для нас становится очевидным, что на горах слева намного меньше шума чем на шариках справа - потому что мы сравниваем найденные на изображениях образы с эталонными (воспоминаниями), откуда и делаем вывод, по количеству отличий - о количестве шума. Всё дело в том, что мы знаем - как обычно выглядят и люди, и шарики, и горы - это и позволяет нам видеть на их изображениях "лишние" пиксели шума.
Точно такой же принцип используется в "свёрточных нейросетях", наиболее широко известных под термином CNN (convolutional neural network), самым популярным примером которых является архитектура U-Net (потому что её схема похожа на букву U): они смотрят на общий план, выделяют на нём смысловые элементы и сравнивают их с накопленным (в ходе обучения) опытом. То что мы назвали бы "посмотреть на картинку шире", в предыдущем примере, отдаляясь от мелкого фрагмента к полному изображению - в терминологии нейросетей называется "свёрткой" (convolution). В процессе свёртки нейросеть, как бы, абстрагируется от отдельных пикселей к смыслу отдельных элементов - а затем, смыслу всей картинки в целом. Свёртка - это, по сути, сжатие (с потерями), в некотором смысле, напоминающее вычисление хеш-суммы: в процессе свёртки исходные данные сжимаются в сотни и тысячи раз (и больше), при этом - у различных исходных данных свёртки так же будут разные (до определённого уровня). Сопоставлять объекты по их "свёрткам" - намного быстрее, чем сравнивать несжатые объекты. Благодаря этому "лайфхаку" нейросети могут в реальном времени обрабатывать визуальные данные даже на чипах мобильных устройств - современных смартфонов.
Значит, берём нейросеть-классификатор - и дополняем свёрткой, если заведомо её там не было. И тут мы понимаем, что классификатор и свёртка - это одно и то же? По сути - как классификатор превращает сотни вводов в десяток выводов - так же может и свёртка, так в чём разница? Разница в параметрах: у сети-классификатора параметры инициализируются случайным образом, после чего итеративно меняются на шаг обучения и вычисленный с помощью цепного правила градиент; а у свёрточных сетей - все параметры "преднастроены с завода" таким специальным образом, который "одним выстрелом бьёт двух зайцев": и данные сжимает, сохраняя при этом смысловые элементы - и выделяет границы перехода (между смысловыми элементами). Да что уж тут говорить - этот метод настолько "волшебный", что с его помощью можно даже нарисовать тени на плоских (двухмерных) объектах! Задумывались когда-нибудь, как работают эти прикольные фильтры в фотошопе? А вот как:
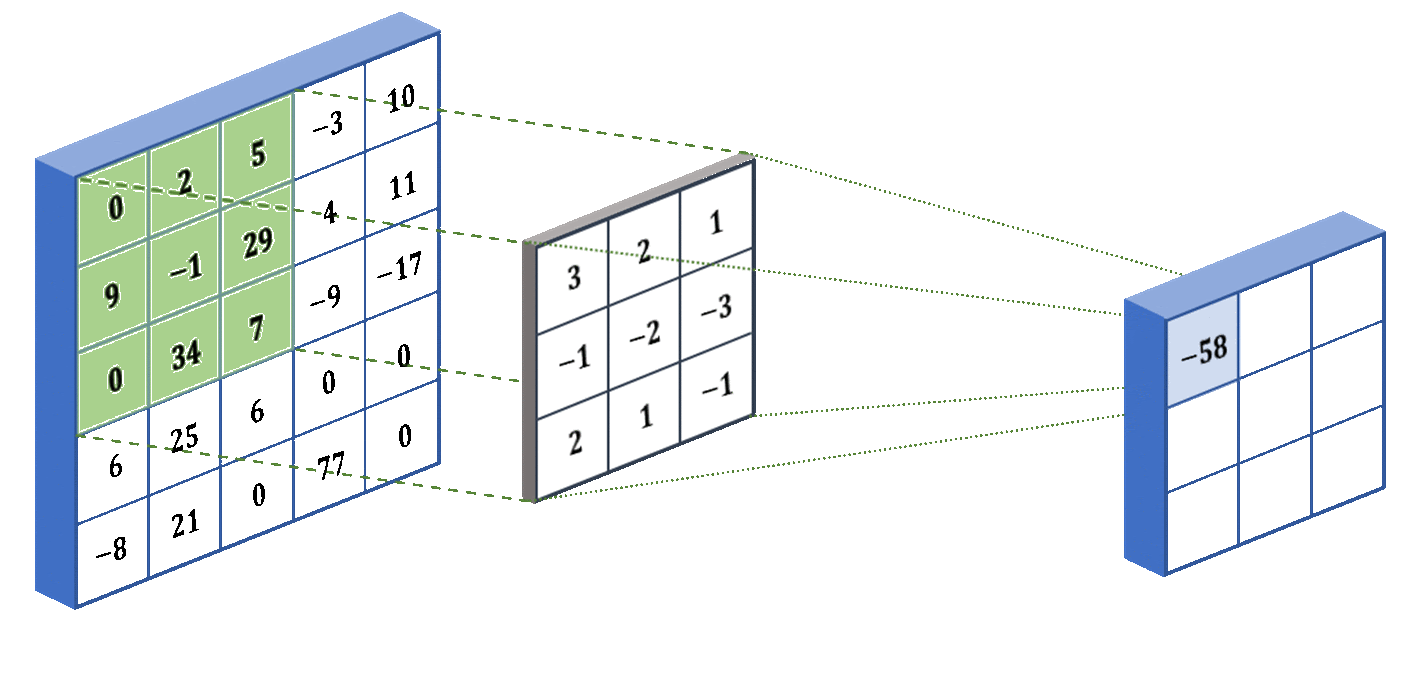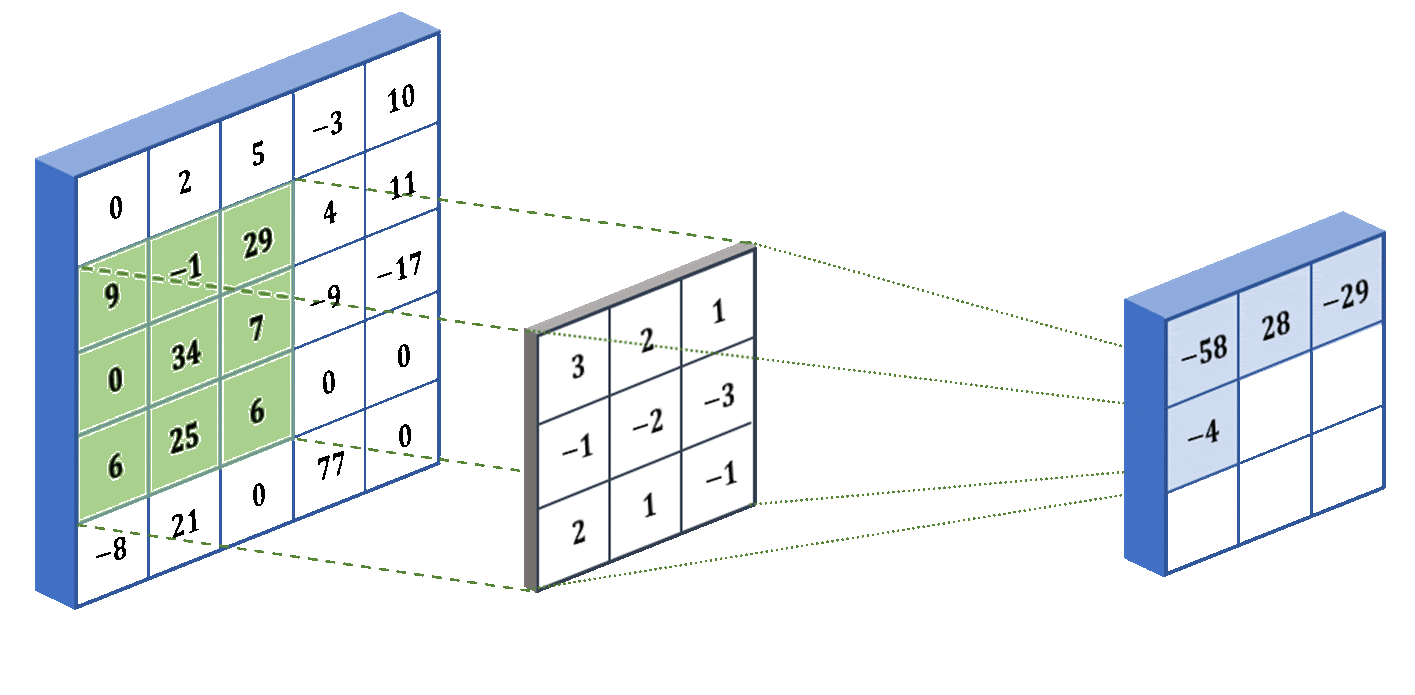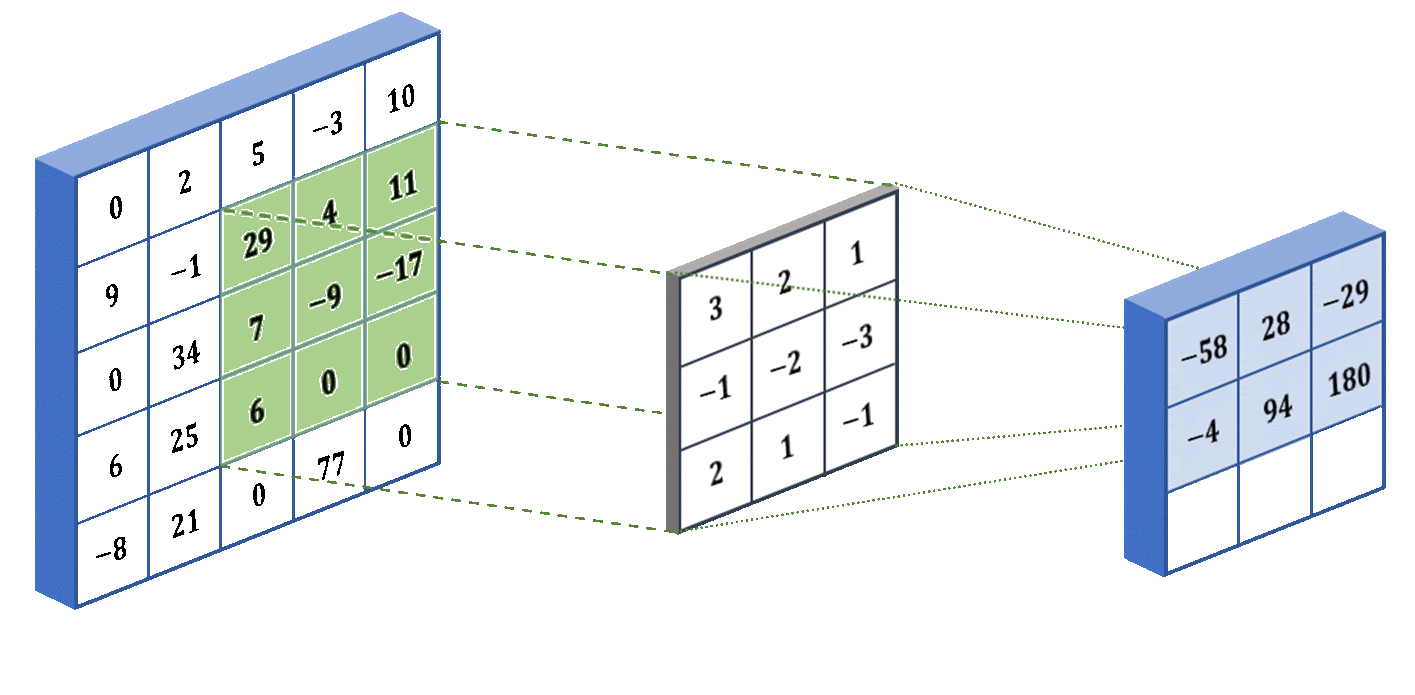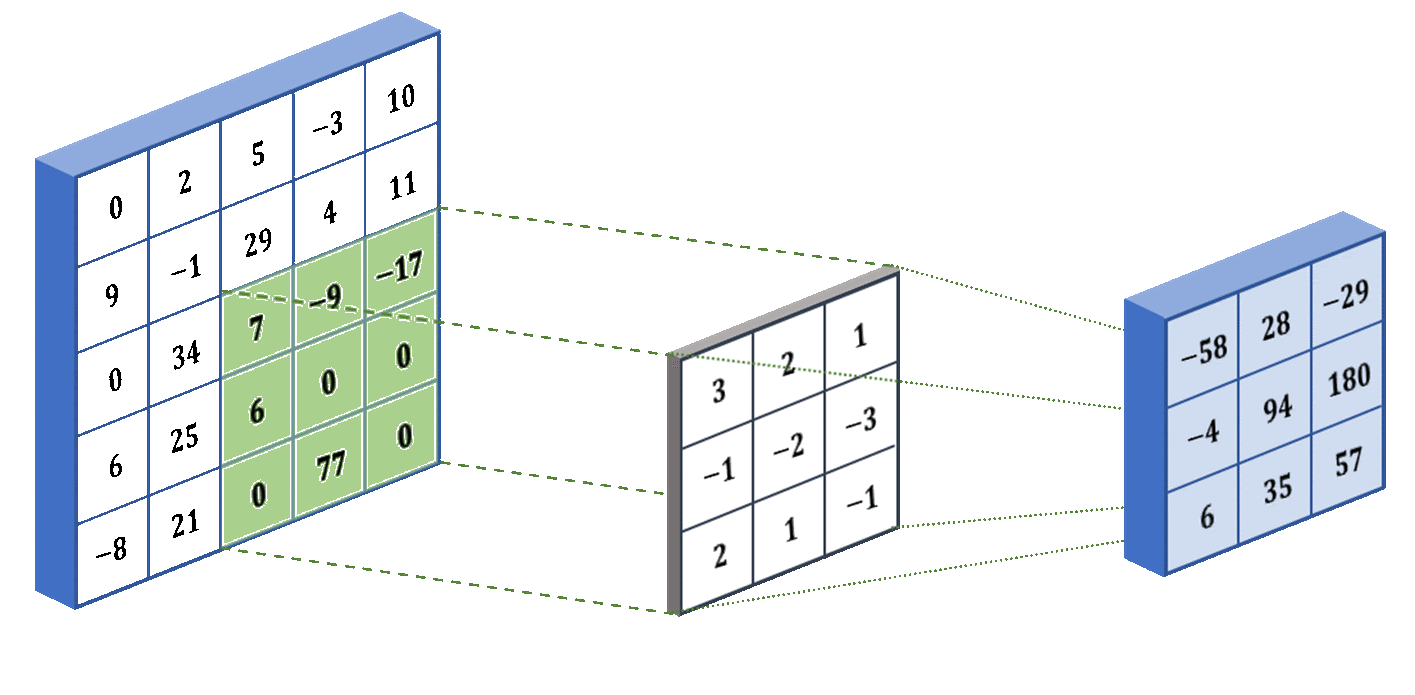
Как видно из анимации выше - работает оно предельно просто: по всей матрице ввода проходит маска (ядро свёртки) с произвольными значениями, функция которой - умножать значения в подлежащих ячейках матрицы на свои, а затем суммировать эти значения по всему ядру в одно результирующее значение для ячейки матрицы свёртки. Как не трудно догадаться - степень сжатия зависит от размера ядра свёртки и количества итераций. Матрицу любого исходного размера можно сжать до размера ядра свёртки - за определённое число итераций.
Так выглядит свёртка на конкретном примере (взял из этой статьи):

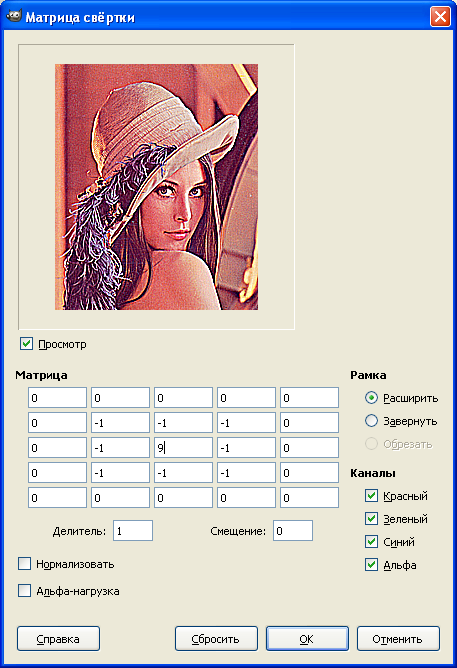
Вот ещё примеры самых "базовых" масок 2х2 и 3х3, раздельные по вертикальным и горизонтальным составляющим:
Маски Робертса:
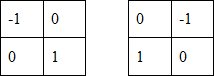

Маски Собеля:
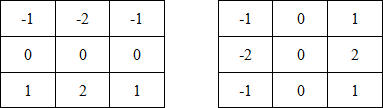

Ядра свёртки Робертса и Собеля - используются для выделения граней на изображениях. Каждая маска по отдельности - выделяет только вертикальные, либо горизонтальные грани; на примерах выше изображены суммы этих свёрток - выделяющие все грани в совокупности.
Если нужно именно сжать исходник, а не выделить грани, то есть и более простой алгоритм свёртки - "Max Pooling" - он просто сохраняет максимальное значение из каждой группы, удаляя все остальные; за один "проход" сжимая исходник в 4 и более раз:
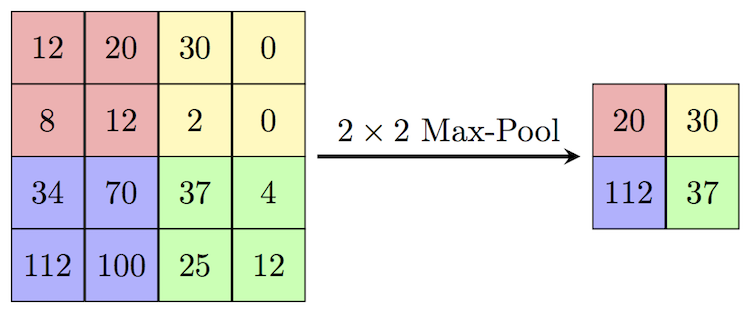
Пулинг максимального - самый распространённый, но далеко не единственный способ пулинга - методов придумали множество, есть среди них и довольно нетривиальные - такие как генетический или пирамидный.
Уместен вопрос - почему пулинг максимальных значений более популярен, чем пулинг, например, средних?

Как видно на сравнении выше - пулинг исходных изображений может привести к довольно непредсказуемым результатам - поэтому обычно пулингу подвергают не исходники, а их свёртки с выделенными переходами:

А вот и та самая U-Net, на схеме которой синими стрелочками изображены операции выделения граней свёрткой, а красными - пулинг максимальных значений:
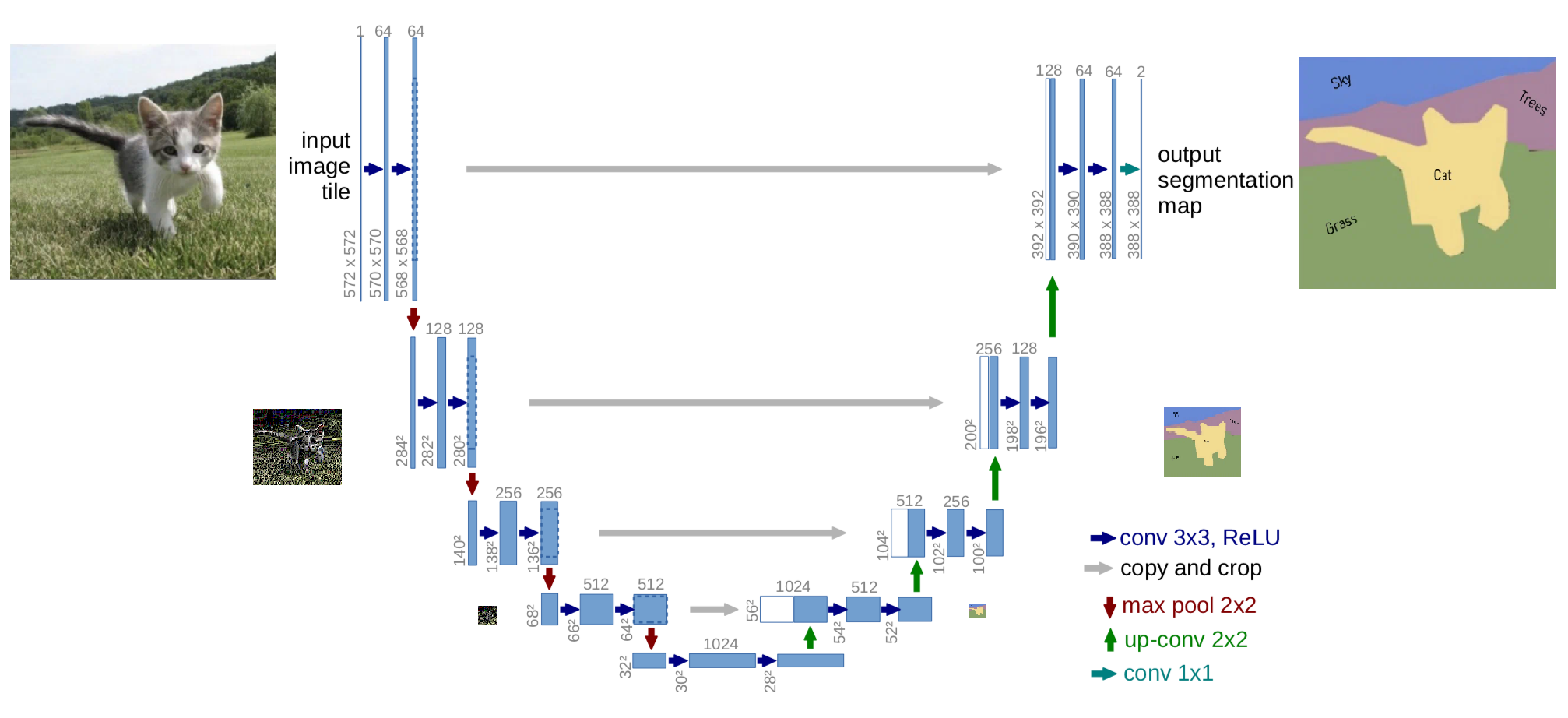
Вернёмся к вопросу распознания и коррекции шума. Если на вход свёрточной нейросети подать картинку с сильными помехами - то свёртка такой нейросети масками, выделяющими границы перехода - лишь усугубит ситуацию: перед такими свёртками, входные данные уместно пропустить через "медианный фильтр" - обычно это маска 3х3 или 5х5, на выходе у которой - самое среднее значение из всех, которые попадают в область маски. Медианный фильтр - эффективное средство подавления случайных аномалий (шума) - но это всё ещё ни в коем смысле не средство восстановления информации.


Так о чём это я? Ах да - нейросети, превращающие текст в картинки. Но какой текст? Где условия? Неужели можно ввести прямо таки что угодно, и нейросеть нарисует?! Лукавят, лукавят эти "дата саентисты"! Что, с руками проблемы? Пальцев многовато? Нет, не туда смотрите. Пальцы, волосы, прочие неестественности - это всё ерунда, которая легко решается нормальным датасетом, архитектурой и обучением. То что нейросети уделяют недостаточно внимания каким-то деталям - как говорится, "дело техники" - пройдёт несколько лет и эти проблемы уйдут в историю. Но есть кое-что, чего "диффузионные" модели не нарисуют - хоть ты тресни! Уже догадываетесь? Вот вам несколько запросов и их результаты - от одной из самых популярных и самых "мощных" среди публично доступных нейросетей - stable diffusion:

Я вижу "mountains", но я не вижу "noise". Может быть, я не так смотрю, или не тот запрос? Попробуем другой, чуть более конкретный:

И снова неудача! Снова - из всего моего длинного и очень конкретно сформулированного запроса, нейросеть поняла только одно слово "nature".
Не сдаёмся (пока бесплатные генерации ещё есть):

Запрошенной разницы между картинками - лично я не вижу. По моему скромному мнению - количество шума с обоих сторон одинаковое.
Широко известная нейросеть ChatGPT прекрасно понимает, что такое пиксели, что такое шум и в чём разница между картинкой низкого разрешения и картинкой высокого разрешения. Современные, хорошо обученные нейросети это понимают, но результат дать не могут. В чём же дело?
А дело всё в последнем элементе таких вот генеративных нейросетей - благодаря которому их полное название - это "Генеративно-состязательные сети" (Generative adversarial network, сокращённо GAN): речь о том самом состязательном элементе этих нейросетей, назначение которого - "лупить палкой" по генератору, если его "творение" хоть чем-то не устраивает состязателя. Именно поэтому генеративно-состязательные сети показывают нам "залипательные" картинки, как бы "отполированные" до блеска - но не могут показать нам всё то, что "состязатель" помечает "браком"; а бракует он всё то, что вызывает у него "смешанные" чувства - все результаты, которые вызывают у нейросети недостаточную (достаточность задаётся администратором) активацию по классам, соответствующим текстовому запросу пользователя, или же если активация по "плохим" классам (тоже задаются администратором) слишком высокая - например, если у нейросети-классификатора, выступающего в роли состязателя, глядя на выдачу псевдослучайного генератора возникает слишком высокий вывод по классу "шум" - то такой состязатель попросит генератор изменить выдачу - но не сильно - на небольшой определённый шаг. Генератор, по запросу состязателя, внесёт изменения в данные на входном слое нейросети (который теперь, как бы, в роли вывода, где формируется картинка) - на что состязатель ему скажет - в правильном ли направлении были внесены изменения или нет. Если направление не правильное - оно меняется, если правильное - то дополняется. Вот так - внося небольшие изменения в данные (например, в цвет пикселей), за множество итераций, данные на входном слое нейросети подгоняются под максимальный вывод по запрошенным классам и минимальный вывод по "запрещённым" классам (которые обычно связаны с шумом и низким качеством изображения, цензурным контентом и "счётчиком пальцев" - в качестве примера).
Выходит, что раньше - нейросети рисовали руки со странными количествами пальцев, теперь же - не могут выполнить запрос, требующий нарисовать руку с числом пальцев, отличным от пяти:
Точно так же нейросети и "восстанавливают" информацию, удалённую шумом: строго говоря, они её не восстанавливают, а заменяют наиболее подходящей по контексту. В отличие от медианного фильтра, по сути просто "размазывающего" картинки, заменяющего шум средним значением окружающих его пикселей - генеративно-состязательная нейросеть работает с пикселями отдельно от их соседей - но в связке со смысловым содержанием, которое они учатся выделять с помощью обучения размеченным датасетом. Благодаря такой логике, нейросети могут восстанавливать тонкие линии (даже в один пиксель) и увеличивать разрешение изображений, "врисовывая" между пикселями исходного изображения наиболее подходящие по смыслу:
Источники и ссылки на дополнительные материалы по теме:
Плагин для Экселя "Nerual Excel" - youtube
Матричные фильтры обработки изображений - хабр
Pooling In Convolutional Neural Networks
Pooling Methods in Deep Neural Networks, a Review - PDF
Классификатор изображений на питоне - youtube
Ряды Тейлора и ряды Фурье в нейросетях - youtube
Оптимизация программы обучения - стохастический градиентный спуск - wikipedia
Свёрточные нейронные сети - wikipedia
ну и моя "записная книжка" - в телеграмме
Публично доступные GAN (авторизация аккаунтом гугл):
https://wepik.com/ai-generate
https://stablediffusionweb.com/
P.S. не советую верить всяким лицам нетрадиционной ориентации, особенно - в части их прогнозов на скорейшее пришествие искусственного сверх-интеллекта и прочих "сингулярностей" - на сегодняшний день это просто смехотворно. Сэм Альтман выдавливает все соки из своего "хайпа", со временем всё больше напоминая эдакую Грету Тундберг в мире нейросетей. Туда же - всех нытиков, кто сетует на нейросети "лишающие" их работы.
Есть лишь один способ угомонить этих "недо-эко-активистов" и остальных плоскоземельщиков - игнорировать их и деликатно презирать всех кто ещё не делает этого. От всей души прошу. Просвещения и всех благ дочитавшим.