Время — это не просто ещё одно измерение
- воскресенье, 31 марта 2024 г. в 00:00:13

Большинство из нас хоть раз в жизни задавались вопросом: «Каково кратчайшее расстояние между двумя точками?». По умолчанию многие дадут тот же ответ, что и Архимед более 2 000 лет назад: прямая линия. Если вы возьмёте плоский лист бумаги и поставите на нём две точки в любом месте, вы сможете соединить эти две точки любой линией, кривой или геометрической траекторией, которую только можно себе представить. До тех пор пока бумага остаётся плоской и никак не изогнутой, прямая линия, соединяющая эти две точки, будет самым коротким путём между ними.
Именно так работают три измерения пространства в нашей Вселенной: в плоском пространстве кратчайшее расстояние между любыми двумя точками — это прямая линия. Это верно независимо от того, как вы вращаете, ориентируете или иным образом располагаете эти две точки. Но наша Вселенная состоит не только из трёх пространственных измерений – она содержит четыре измерения, пространство и время. Легко взглянуть на это и сказать: «О, ну три из них — пространство, а одно — время, вот мы и получаем пространство-время», — и это правда, но это не вся история. В конце концов, кратчайшее расстояние между двумя событиями в пространстве-времени уже не является прямой линией. И вот что говорит об этом наука.
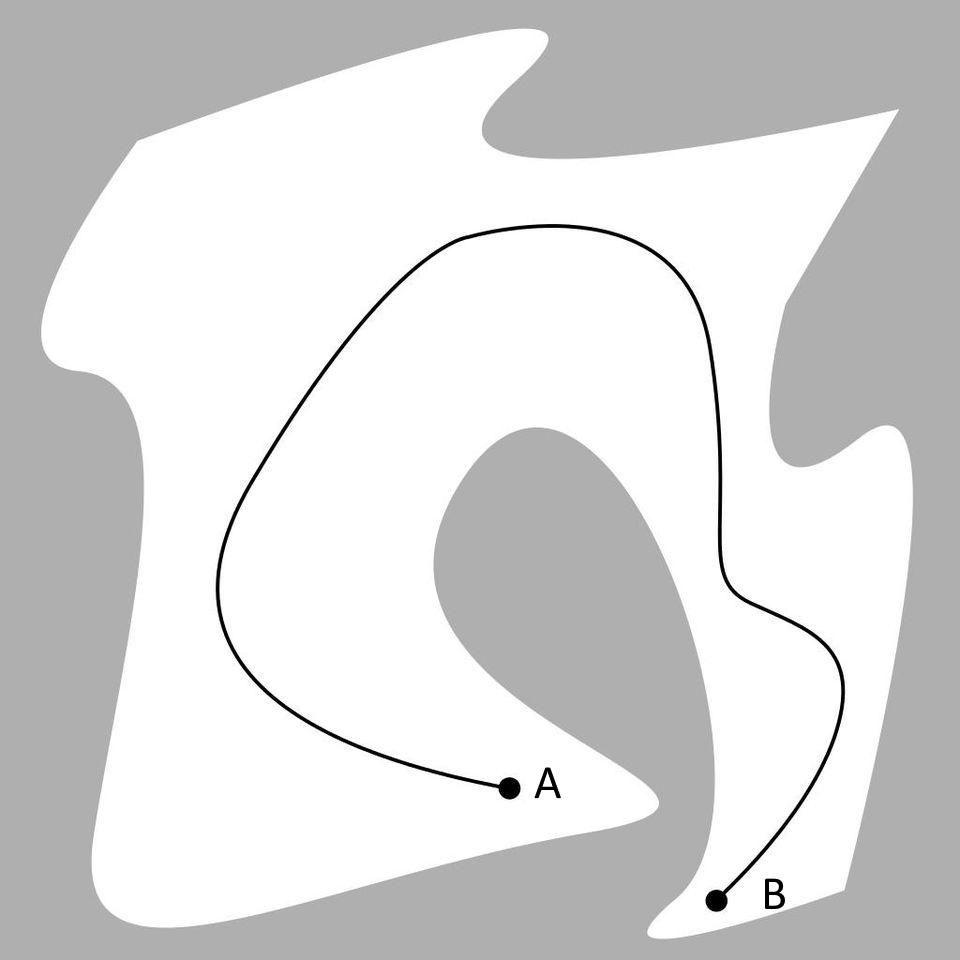
Для большинства из нас первое знакомство с идеей о том, что прямая линия является кратчайшим расстоянием между двумя точками, произошло не самым очевидным образом: при изучении теоремы Пифагора. Возможно, вы помните теорему Пифагора как правило о прямоугольных треугольниках: если возвести в квадрат каждую из коротких сторон и сложить их вместе, то получится квадрат длинной стороны. Говоря языком математики, если короткие стороны равны a и b, а длинная сторона равна c, то уравнение, связывающее их, будет a² + b² = c².
Подумайте, что это значит, но не с точки зрения чистой математики, а с точки зрения расстояний. Это значит, что если вы перемещаетесь по одному из пространственных измерений на определённую величину (например, a), а затем перемещаетесь по перпендикулярному измерению на другую величину (например, b), то расстояние между тем, где вы начали, и тем, где вы оказались, равно c, как это определяется теоремой Пифагора. Другими словами, расстояние между любыми двумя точками на плоскости, когда эти точки отстоят друг от друга на a в одном измерении и на b в другом, равно c, где c = √(a² + b²).

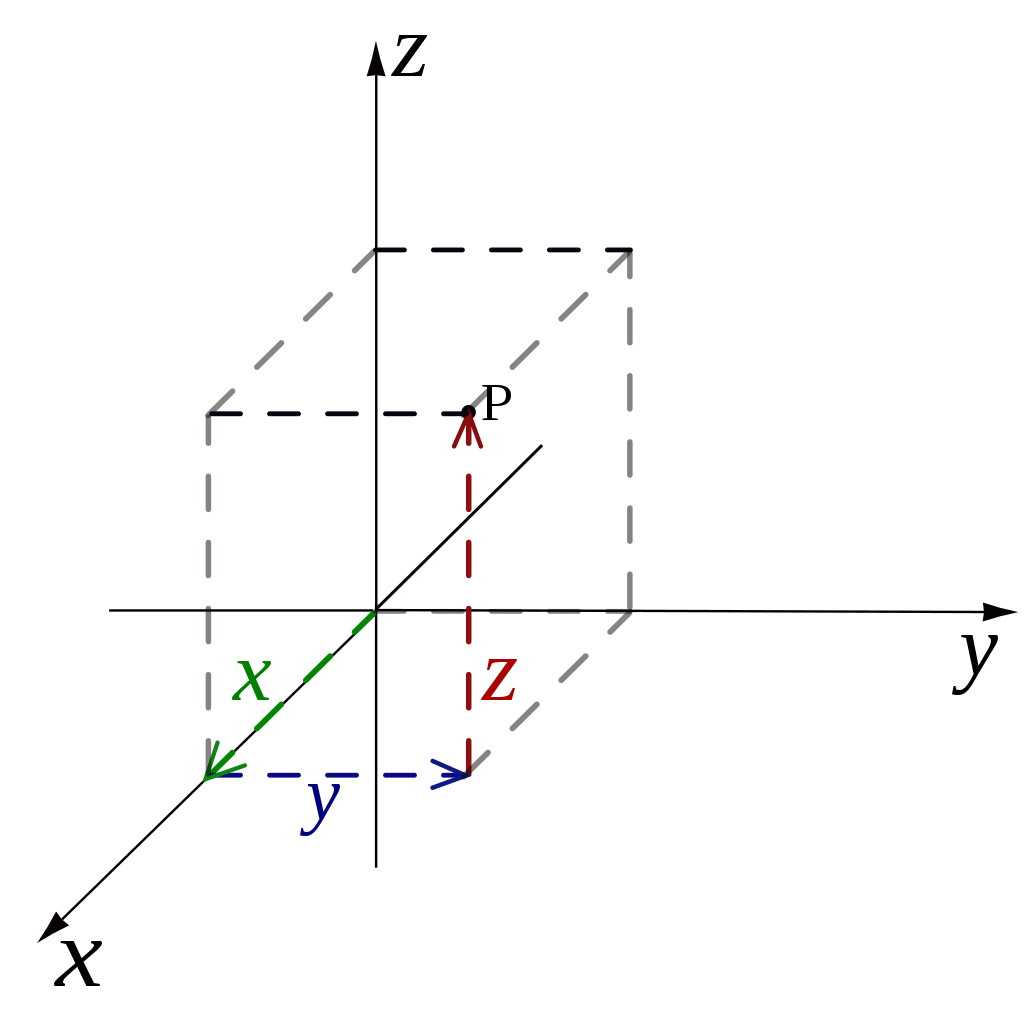
В нашей Вселенной, конечно, мы не ограничены плоскостью, как лист бумаги. В нашей Вселенной есть не только длина и ширина (или направления x и y, если хотите), но и глубина (или направление z). Если вы хотите определить расстояние между любыми двумя точками в пространстве, метод останется точно таким же, как и в двух измерениях, только с учётом одного дополнительного. Какое бы расстояние ни разделяло две точки в направлениях x, y и z, вы можете вычислить общее расстояние между ними точно так же, как и раньше.
Только из-за дополнительного измерения расстояние между ними — назовём его d — будет равно d = √(x² + y² + z²). Это уравнение может показаться пугающим, но оно просто говорит, что расстояние между любыми двумя точками определяется прямой линией, соединяющей их: линией, которая учитывает расстояние между двумя точками во всех трёх измерениях: в направлении x, в направлении y и в направлении z вместе взятых.
Одно из интересных и важных следствий того, что расстояние между двумя точками является прямой линией, заключается в том, что абсолютно неважно, как вы определите измерения x, y и z. Вы можете изменить координаты так, чтобы оси x, y и z были направлены в любую сторону (оставаясь при этом взаимно перпендикулярными), либо повернуть соединяющую эти две точки линию на любой угол в любом направлении, и расстояние между ними не изменится вообще.
Конечно, отдельные координаты изменятся, если вы посмотрите на это с другого угла или повернёте линию, соединяющую эти две точки, поскольку ваши определения длины, ширины и глубины будут меняться относительно друг друга для этой линии при повороте. Но общее расстояние между этими двумя точками не меняется вообще; расстояние между этими точками остаётся, как мы говорим, «инвариантным», или неизменным, независимо от того, как вы поворачиваете всю картину.

Теперь давайте рассмотрим не только пространство, но и время. Вы можете подумать: «Ну, если время — это тоже измерение, то расстояние между любыми двумя точками в пространстве-времени будет работать точно так же». Например, если мы представим измерение времени как t, вы можете подумать, что расстояние будет прямой линией, соединяющей две точки через три пространственных измерения, а также измерение времени. В математических терминах вы можете подумать, что уравнение для расстояния между любыми двумя точками будет выглядеть примерно так: d = √(x² + y² + z² + t²).
В конце концов, это практически то же самое изменение, которое мы сделали, когда переходили от двух измерений к трём, только на этот раз мы переходим от трёх измерений к четырём. Это вполне разумный шаг, который описывает, как выглядела бы реальность, если бы у нас было не три, а четыре измерения пространства.
Но у нас нет четырёх измерений пространства; у нас есть три измерения пространства и одно измерение времени. И, несмотря на то, что может подсказать вам интуиция, время — это не «просто ещё одно измерение».

Время как измерение отличается от измерений пространства двумя аспектами. Первый не так критичен: вы не можете сопоставить пространство (которое является измерением расстояния) и время (которое является измерением, ну, времени) друг другу без какого-либо способа преобразования одного в другое. К счастью, одним из великих открытий теории относительности Эйнштейна стало то, что между расстоянием и временем существует важная, фундаментальная связь: скорость света или, эквивалентно, любой частицы, не имеющей массы покоя, путешествующей по Вселенной.
Скорость света в вакууме — 299 792 458 метров в секунду — точно указывает нам, как связать наше движение в пространстве с нашим движением во времени: с помощью самой этой фундаментальной константы. Когда мы используем такие термины, как «один световой год» или «одна световая секунда», мы говорим о расстояниях в терминах времени: например, о расстоянии, которое свет проходит за один год (или одну секунду). Если мы хотим преобразовать «время» в расстояние, нам нужно умножить его на скорость света в вакууме.

Но второй аспект требует огромного скачка в понимании: он ускользал от величайших умов конца XIX и начала XX веков. Ключевая идея заключается в том, что мы все движемся во Вселенной одновременно в пространстве и времени. Если мы просто сидим неподвижно и не перемещаемся в пространстве, тогда мы движемся во времени с очень конкретной скоростью, которая нам всем хорошо знакома: одна секунда в секунду.
Однако — и это ключевой момент — чем быстрее вы движетесь в пространстве, тем медленнее вы двигаетесь во времени. С другими измерениями дело обстоит иначе: например, ваше движение в пространстве по измерению x совершенно не зависит от вашего движения по измерениям y и z. Но ваше общее движение через пространство, относительно любого другого наблюдателя, определяет ваше движение во времени. Чем больше вы движетесь в одном из них (пространстве или времени), тем меньше вы движетесь в другом.
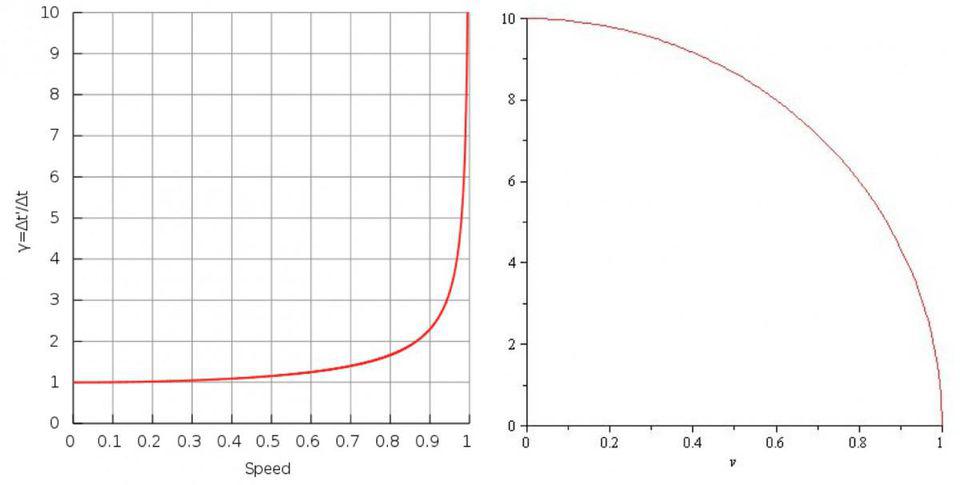
Именно поэтому относительность Эйнштейна даёт нам такие понятия, как замедление времени и сокращение длины. Если вы двигаетесь на очень низких скоростях по сравнению со скоростью света, вы не заметите этих эффектов: кажется, что время движется со скоростью одна секунда в секунду для всех, а длина кажется одинаковой для всех при скоростях, обычно достижимых на Земле.
Но когда вы приближаетесь к скорости света — или, скорее, когда вы воспринимаете объект, скорость которого относительно вас близка к скорости света, — вы заметите, что он сжимается вдоль направления относительного движения, а его часы кажутся идущими медленнее по сравнению с вашими собственными часами.
Причина этого, как понял Эйнштейн, проста: скорость света одинакова для всех наблюдателей. Если представить часы на основе фотона, отражающегося от двух зеркал, то наблюдение за чужими часами, движущимися со скоростью, близкой к скорости света, неизбежно приведёт вас к выводу, что эти часы идут медленнее, чем ваши собственные.

Но здесь есть ещё более глубокий смысл, который поначалу не понял даже сам Эйнштейн. Если рассматривать время как измерение, умножить его на скорость света и — вот большой скачок — рассматривать его как мнимое, а не реальное, то мы можем определить «интервал пространства-времени» так же, как мы определяли расстояние ранее. Только, поскольку мнимое число i — это просто √(-1), это означает, что интервал пространства-времени на самом деле равен d = √(x² + y² + z² — c²t²). (Обратите внимание на знак минуса, прикреплённый к временной координате!)
Другими словами, преобразование от «движения через пространство или расстояния в пространстве» к «движению через время или расстоянию во времени» — это тоже вращение, но вращение не в декартовых координатах пространства (где x, y и z — все действительные числа), а в гиперболических координатах пространства-времени, где если пространственные координаты действительны, то временная координата должна быть мнимой.
По счастливому стечению обстоятельств, человеком, который первым сложил эти кусочки головоломки воедино, был бывший учитель Эйнштейна Герман Минковский, который в 1907 году заметил:
«Отныне пространство само по себе и время само по себе обречены превратиться в простые тени, и только некий союз этих двух явлений сохранит независимую реальность».
Благодаря математической строгости Минковского концепция пространства-времени не только родилась, но и осталась с нами надолго.

Примечательно то, что Эйнштейн, которому не хватило математической проницательности, чтобы понять, как именно измерение времени связано с тремя традиционными измерениями пространства, всё же смог собрать воедино физическую картину происходящего. Увеличение скорости вашего движения через пространство уменьшает ваше движение через время, а увеличение скорости вашего движения через время уменьшает ваше движение через пространство. Все измерения пространства и времени имеют смысл только по отношению к наблюдателю и зависят от относительного движения наблюдателя и наблюдаемого.
И всё же пространственно-временной интервал остаётся неизменным. Независимо от того, кто наблюдает и как быстро он движется, движение любого объекта в пространстве-времени — это то, с чем могут согласиться все наблюдатели. В некотором смысле успех теории относительности стал ещё более впечатляющим в свете того, как Минковский оценил Эйнштейна. В разговоре со своим (впоследствии) учеником Максом Борном Минковский сказал следующее:
«Для меня [относительность] стала огромным сюрпризом, потому что в студенческие годы Эйнштейн был настоящим лентяем. Он вообще никогда не задумывался о математике».
К счастью, в физике конечным арбитром научной истины является сама Вселенная, а не чьё-либо мнение.