news.shamcode.ru | Визуализация линий напряженности и движений электростатических зарядов, симулирование движения плане

Визуализация линий напряженности и движений электростатических зарядов, симулирование движения плане

понедельник, 10 февраля 2020 г. в 00:24:00

Python
Алгоритмы
Визуализация данных
Физика
Астрономия

Привет, сегодня я хочу вам предложить наглядное пособие по моделированию некоторых физических процессов и показать как получить красивые изображения и анимации. Осторожно много картинок.

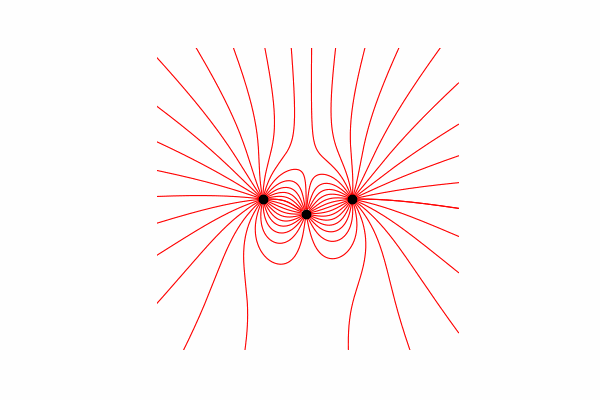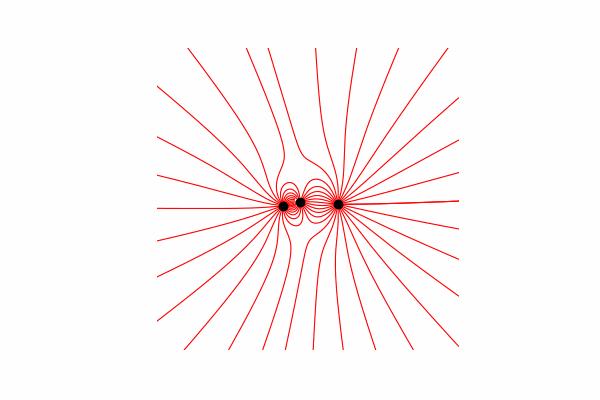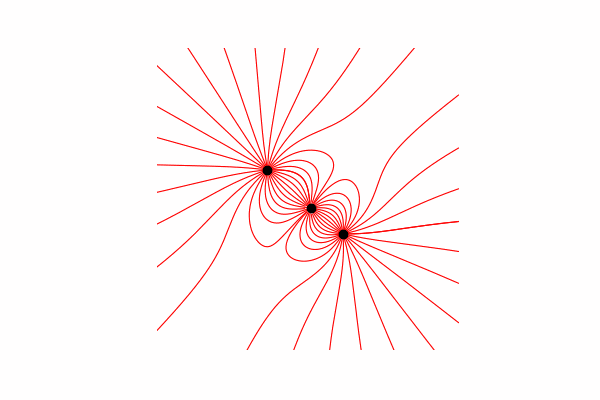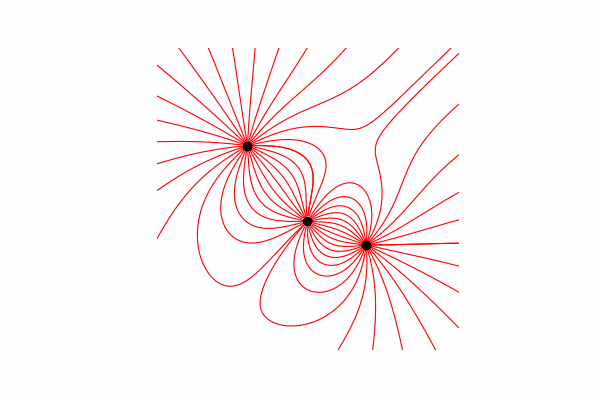
Весь код можно найти в Google colab.

Теория

Для начала нам понадобится небольшой теоретический минимум по этой теме. Начнем с понимания что такое линии напряженности и как их считать. По сути данные линии являются слиянием множества векторов напряжённости, которую можно посчитать так:

$E=\frac{k*|q|}{r^2}$ .

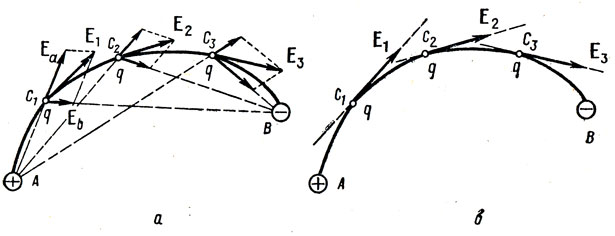
Метод вычисления E

Я рассчитывал вектор напряженности через подобие треугольников, получая тем самым проекции на оси x и y dx и dy соответственно.

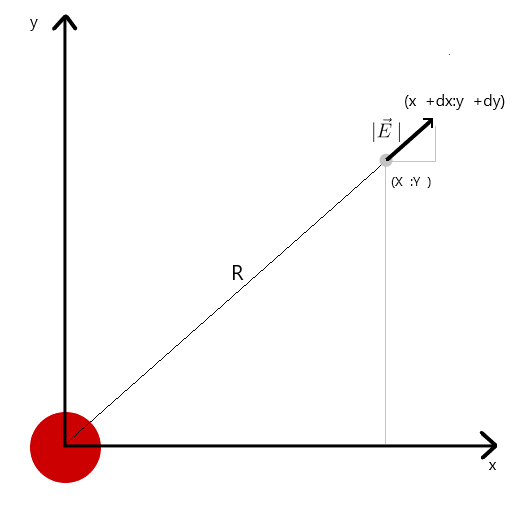
Из подобия следует, что радиуса вектора от заряда до точки в пространстве r и длинны вектора напряженности E равно отношению проекций этих векторов (x1 и dx соответственно)

$\frac{R}{E}=\frac{x}{dx}=\frac{y}{dy}$ . Формула результирующего вектора

$\vec{E}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{E}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{E}_i|}{R_i} \end{array}\right) \qquad$
с этими знаниями получаем первый результат.

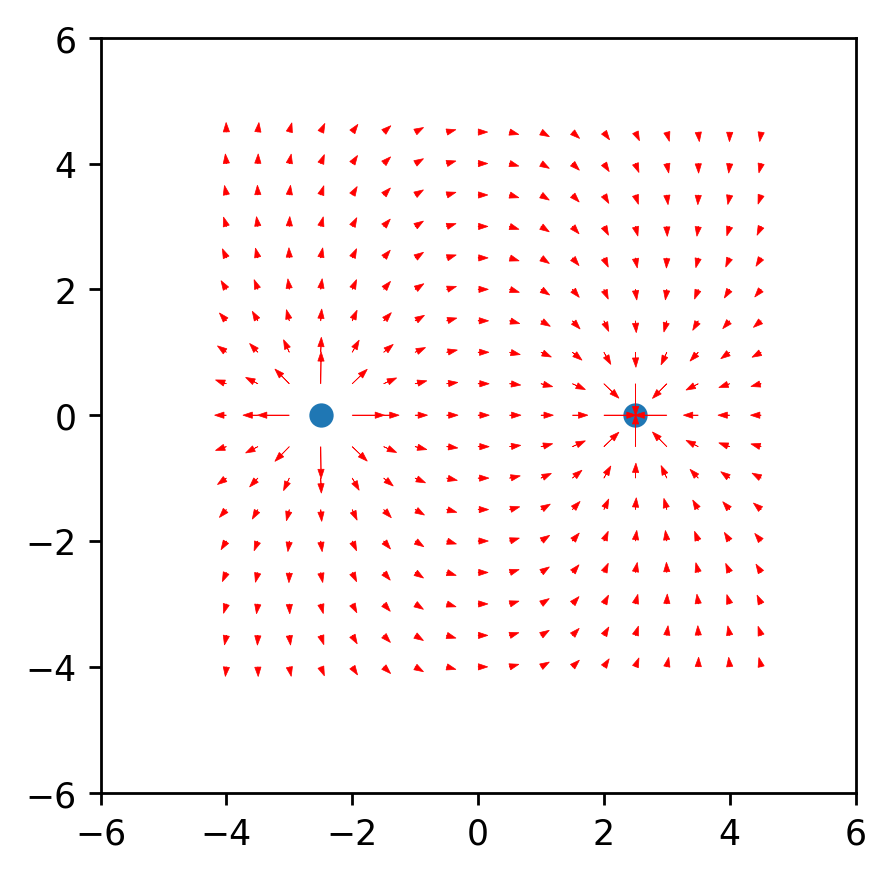
Функция расчета проекций

def E(q_prop, xs, ys, nq): #q_prop=[[xq1, yq1, q1, mq1, vxq1, vyq1], [xq2, yq2, q2, mq2, vxq2, vyq2] ... ] 
    l=1
    k=9*10**9
    Ex=0
    Ey=0
    c=0
    for c in range(len(q_prop)):#проходимся по всем зарядам в массиве вычисляем проекции напряженности в заданной точке и обновляем значение результирующей напряженности
        q=q_prop[c]
        r=((xs-q[0])**2+(ys-q[1])**2)**0.5
        dEv=(k*q[2])/r**2
        dEx=(xs-q[0])*(dEv/r)*l
        dEy=(ys-q[1])*(dEv/r)*l

        Ex+=dEx
        Ey+=dEy
    return Ex, Ey

Метод построения линий

Для начала нужно определиться с начальной и конечной точкой, откуда будет идти линия и докуда. Началом являются точки на окружности с радиусом r вокруг заряда, а концом точки отдаленные от зарядов не более чем на r.

код для определения начальных точек

theta = np.linspace(0, 2*np.pi, n)
mask=q_prop[ q_prop[:,2]>0 ]#оставляем только положительные заряды 
for cq in range(len(mask)):
    qmask=mask[cq]
    xr = r_q*np.cos(theta)+qmask[0]#определение х-ов точек окружности вокруг заряда
    yr = r_q*np.sin(theta)+qmask[1]#аналогично

Так-же стоит сказать, что линии строятся только из положительных зарядов.
И наконец построение линий. Для этого мы из начальной точки строим линию вектора напряженности в ней, обновляем начальную точку на конец построенной линии и повторяем пока не будет достигнуто условия окончания, названные выше.

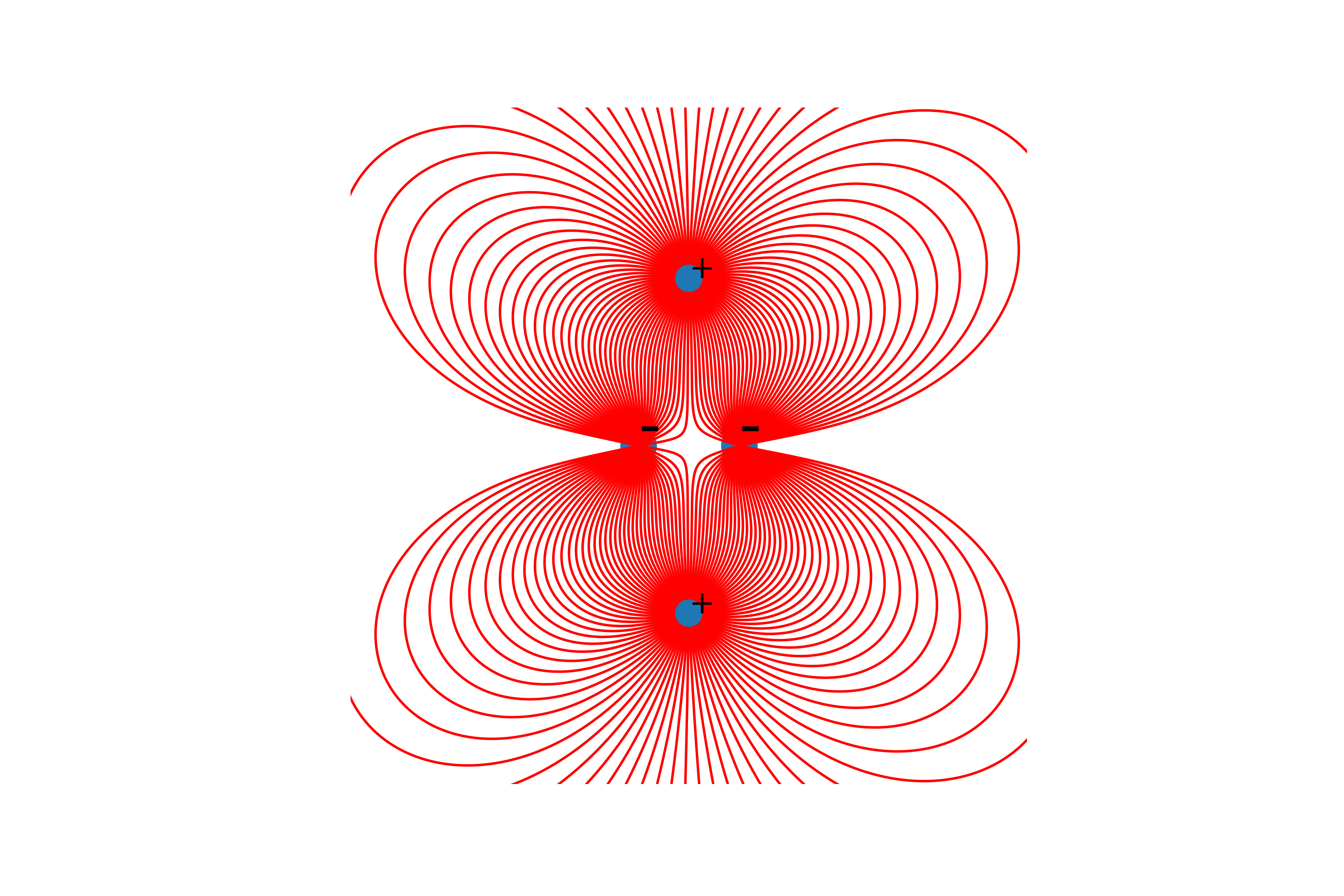
функция вычисления координат линий

def Draw(size, q_prop,r_q, n):
  
  linen=np.empty((np.count_nonzero(q_prop[:,2]>0),n, 2000000), dtype=np.float64)
  linen[:] = np.nan
  theta = np.linspace(0, 2*np.pi, n)
  mask=q_prop[ q_prop[:,2]>0 ][ q_prop[q_prop[:,2]>0][:,3]==1 ]
  for cq in range(len(mask)):
    qmask=mask[cq]
    x11 = r_q*np.cos(theta)+qmask[0]
    x22 = r_q*np.sin(theta)+qmask[1]
    for c in range(len(x11)):

      xs=x11[c]
      ys=x22[c]

      lines=np.empty((2,1000000), dtype=np.float64)
      lines[:]=np.nan
      stop=0
      nnn=0
      
      lines[0][nnn]=xs
      lines[1][nnn]=ys
      while  abs(xs)<size+2 and abs(ys)<size+2: 
        nnn+=1

        for cq1 in range(len(q_prop)):
          q=q_prop[cq1]
          if ((ys-q[1])**2+(xs-q[0])**2)**0.5<r_q/2 :
            stop=1
            break
        if stop==1:
          break
        dx, dy = E1(q_prop,xs,ys)

        xs+=dx
        ys+=dy
        lines[0][nnn]=xs
        lines[1][nnn]=ys
       
      linen[cq,c,:]=lines.reshape(-1)

  return linen

Взаимодействие между зарядами

Чтобы отразить их взаимодействие, нужно изменять его координаты и скорость через каждое маленькое время dt.

$x+=\frac{E_x \cdot q \cdot dt^2}{2\cdot m} + v_x\cdot dt$

$y+=\frac{E_y \cdot q \cdot dt^2}{2\cdot m} + v_y \cdot dt$

$v_x+= \frac{E_x \cdot q \cdot dt}{ m}$

$v_y+= \frac{E_y \cdot q \cdot dt}{ m}$

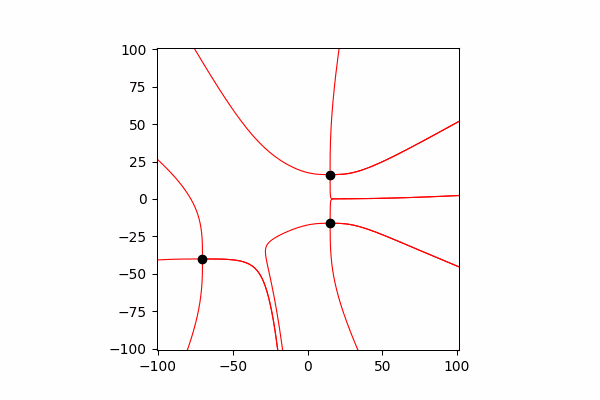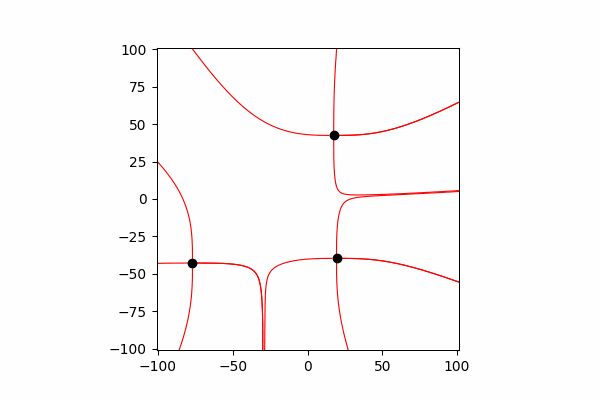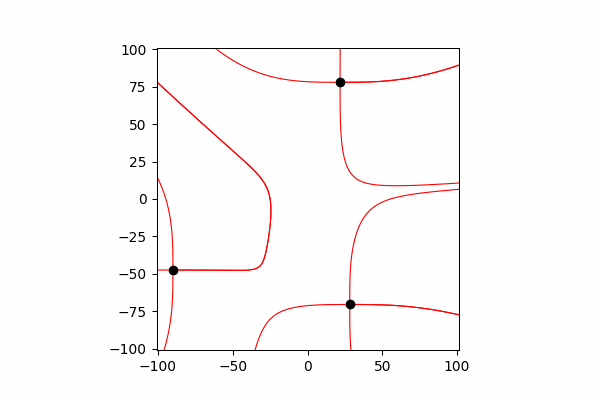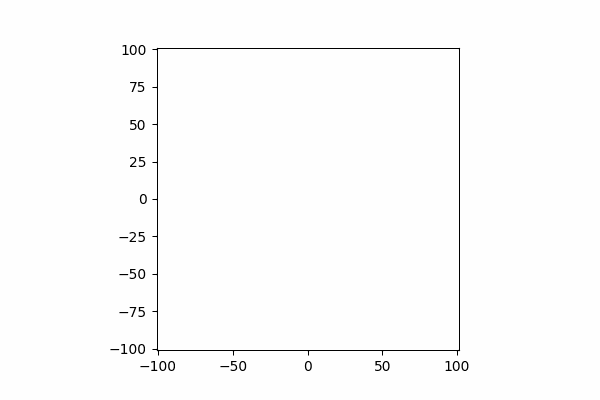
Функция обновления координат и проекций скоростей зарядов

def Update_all(q_prop):
  vx=0
  vy=0
  x=0
  y=0
  q_prop_1=np.copy(q_prop)
  for c in range(len(q_prop)):#проход по зарядам и обновление их координат и проекций скоростей
    xs=q_prop[c][0]
    ys=q_prop[c][1]
    q =q_prop[c][2]
    m =q_prop[c][3]
    vx=q_prop[c][4]
    vy=q_prop[c][5]
    Ex, Ey= E(q_prop, xs, ys, c)

    x=(((Ex*q)/m)*dt**2)/2+vx*dt+xs
    y=(((Ey*q)/m)*dt**2)/2+vy*dt+ys
    vx+=((Ex*q)/m)*dt
    vy+=((Ey*q)/m)*dt
    #print(q_prop[c]-[x,y,q,m,vx,vy])
    q_prop_1[c]=[x,y,q,m,vx,vy]
  
  return q_prop_1#возвращение обновлённого массива характеристик зарядов

Гравитация

На основе имеющегося кода я написал симулятор, отражающий движения тел под действием гравитации. Изменения в коде в основном для функции напряженности т.к. теперь будет считаться ускорение по похожей формуле.

$g=\frac{G*m}{r^2}$

$\vec{g}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{g}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{g}_i|}{R_i} \end{array}\right) \qquad$

Планеты стартуют с оси х в перигелийном расстояние и с перигелийной скоростью. Все значения планет и солнца (массы, расстояния, экстренциситеты) из справочника.
Анимация для первых 4 планет + cолнца.

Жду критику и предложений. До свидания.