https://habr.com/post/423093/- Криптография
- Информационная безопасность
- Python
 случайные числа вкуснее, если их немножко поперчить
случайные числа вкуснее, если их немножко поперчить
Будем сочетать теорию с практикой — покажем, что улучшение энтропии случайных последовательностей возможно, после чего посмотрим исходные коды, которые это делают.
Очень хотелось написать про то, что качественная, то есть высокоэнтропийная, генерация случайных чисел критически важна при решении огромного числа задач, но это, наверно, лишнее. Надеюсь, всем это и так прекрасно известно.
В погоне за качественными случайными числами люди изобретают весьма остроумные приспособления (см. например
здесь и
здесь). В принципе, весьма неплохие источники случайности встроены в API операционных систем, но дело серьёзное, и нас всегда немножко гложет червячок сомнения: а достаточно ли хорош тот ГСЧ, который я использую, и не подпорчен ли он… скажем так, третьими лицами?
Немножко теории
Для начала покажем, что при правильном подходе качество имеющегося ГСЧ невозможно ухудшить. Простейший правильный подход — это наложение на
основную последовательность любой другой через операцию XOR.
Основной последовательностью может быть, например, системный ГСЧ, который мы уже считаем неплохим, но некоторые сомнения всё же есть, и у нас возникло желание подстраховаться.
Дополнительной последовательностью может быть, например, генератор псевдослучайных чисел, выдача которого выглядит неплохо, но мы знаем, что его реальная энтропия весьма невысока.
Результирующей последовательностью будем называть результат применения операции XOR к битам основной и дополнительной последовательностей.
Существенный нюанс: основная и дополнительная последовательности должны быть независимыми друг от друга. То есть их энтропия должна браться из принципиально разных источников, взаимозависимость которых невозможно вычислить.
Обозначим как
x очередной бит основной последовательности, а
y — соответствующий ему бит дополнительной. Бит результирующей последовательности обозначим как
r:
r = x⊕y
Первая попытка доказать. Попробуем пройти через информационную энтропию
x,
y и
r. Вероятность нулевого
x обозначим как
px0, а вероятность нулевого
y как
py0. Информационные энтропии
x и
y считаем по формуле Шеннона:
H
x = − (p
x0 log
2p
x0 + (1−p
x0) log
2(1−p
x0))
H
y = − (p
y0 log
2p
y0 + (1−p
y0) log
2(1−p
y0))
Ноль в результирующей последовательности появляется тогда, когда на входе два нуля либо две единицы. Вероятность нулевого r:
p
r0 = p
x0 p
y0 + (1−p
x0) (1−p
y0)
H
r = − (p
r0 log
2p
r0 + (1−p
r0) log
2(1−p
r0))
Для того, чтобы доказать неухудшаемость основной последовательности, нужно доказать, что
Hr − Hx ≥ 0 для любых значений
px0 и
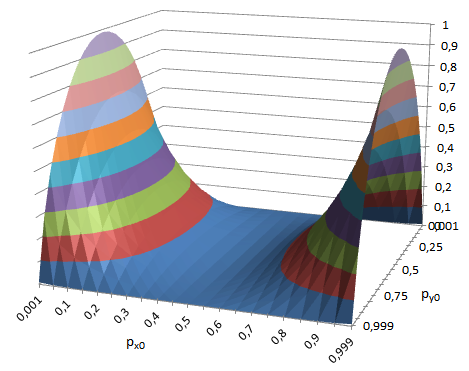
py0. Аналитически это доказать у меня не получилось, но визуализированный расчёт показывает, что прирост энтропии образует гладкую поверхность, нигде не собирающуюся уходить в минус:
Например, если к перекошенному основному сигналу c
px0=0.3 (энтропия 0.881) добавляем сильно перекошенный дополнительный с
py0=0.1, получаем результат
pr0=0.66 с энтропией 0,925.
Итак, энтропию невозможно испортить, но это пока не точно. Поэтому нужна вторая попытка. Впрочем, через энтропию тоже можно провести доказательство. Схема (все шаги достаточно простые, сами можете проделать):
- Доказываем, что энтропия имеет максимум в точке p0=1/2.
- Доказываем, что при любых px0 и py0 значение pr0 не может быть дальше от 1/2, чем px0.
Вторая попытка доказать. Через способность угадывать. Допустим, злоумышленник априорно имеет некоторую информацию об основной и дополнительной последовательностях. Обладание информацией выражается в способности с некоторой вероятностью заранее угадывать значения
x,
y и, как следствие,
r. Вероятности угадать
x и
y обозначим соответственно как
gx и
gy (от слова guess). Бит результирующей последовательности угадывается либо тогда, когда оба значения угаданы верно, либо тогда, когда оба неверно, поэтому вероятность угадывания получается такая:
g
r = g
x g
y + (1−g
x) (1−g
y) = 2 g
x g
y − g
x − g
y + 1
Когда у нас есть идеальный угадыватель, имеем
g=1. Если нам ничего неизвестно,
g равно… нет, не нулю, а 1/2. Именно такая вероятность угадывания получается, если мы будем принимать решение подбрасыванием монетки. Весьма интересный случай, когда
g<1/2. С одной стороны, такой угадыватель где-то внутри себя обладает данными об угадываемой величине, но зачем-то инвертирует свою выдачу, и таким образом становится
хуже монетки. Запомните, пожалуйста, словосочетание «хуже монетки», оно нам ниже пригодится. С точки зрения математической теории связи (и, как следствие, привычной нам количественной теории информации) эта ситуация абсурдна, так как это уже будет не теория информации, а теория дезинформации, но по жизни такое положение дел имеем существенно чаще, чем того нам хотелось бы.
Рассмотрим предельные случаи:
- gx = 1, то есть последовательность x полностью предсказуемая:
gr = gx gy + (1−gx) (1−gy) = 1 gy + (1−1) (1−gy) = gy
То есть вероятность угадывания результата равна вероятности угадывания дополнительной последовательности.
- gy = 1: Аналогично предыдущему. Вероятность угадывания результата равна вероятности угадывания основной последовательности.
- gx = 1/2, то есть последовательность x полностью непредсказуемая:
gr = 2 gx gy − gx − gy + 1 = 2/2 gy − 1/2 − gy +1 = gy − gy + 1/2 = 1/2
То есть добавление любой дополнительной последовательности не ухудшает полную непредсказуемость основной.
- gy = 1/2: Аналогично предыдущему. Добавление полностью непредсказуемой дополнительной последовательности делает результат полностью непредсказуемым.
Для того, чтобы доказать, что добавление дополнительной последовательности к основной ничем не поможет злоумышленнику, нам нужно выяснить, при каких условиях
gr может быть больше
gx, то есть
2 g
x g
y − g
x − g
y + 1 > g
x
Переносим g
x из правой части в левую, а g
y и 1 в правую:
2 g
x g
y − g
x − g
x > g
y − 1
2 g
x g
y − 2 g
x > g
y − 1
Выносим в левой части 2g
x за скобки:
2 g
x (g
y − 1) > g
y − 1
Поскольку у нас g
y меньше единицы (предельный случай, когда g
y=1, мы уже рассмотрели), то превратим g
y−1 в 1−g
y, не забыв поменять «больше» на «меньше»:
2 g
x (1 − g
y) < 1 − g
y
Сокращаем «1−g
y» и получаем условие, при котором добавление дополнительной последовательности улучшит злоумышленнику ситуацию с угадыванием:
2 g
x < 1
g
x < 1/2
То есть
gr может быть больше
gx только тогда, когда угадывание основной последовательности
хуже монетки. Тогда, когда наш предсказатель занят сознательным саботажем.
Несколько дополнительных соображений про энтропию.
- Энтропия — на редкость мифологизированное понятие. Информационная — в том числе. Это очень мешает. Часто информационная энтропия представляется как некая тонкая материя, которая либо объективно присутствует в данных, либо нет. На самом деле информационная энтропия — это не то, что присутствует в самом сигнале, а количественная оценка априорной осведомлённости получателя сообщения относительно самого сообщения. То есть это не только о сигнале, но и о получателе. Если получатель заранее про сигнал совсем ничего не знает, информационная энтропия переданной двоичной единицы равна строго 1 бит вне зависимости от того, как был получен сигнал и что он собой представляет.
- У нас есть теорема о сложении энтропий, согласно которой суммарная энтропия независимых источников равна сумме энтропий этих источников. Если бы мы соединяли основную последовательность с дополнительной через конкатенацию, мы бы сохранили энтропии источников, но получили бы плохой результат, потому что в нашей задаче нужно оценивать не суммарную энтропию, а удельную, в пересчёте на отдельный бит. Конкатенация источников даёт нам удельную энтропию результата, равную среднему арифметическому энтропий источников, и энтропийно слабая дополнительная последовательность естественным образом ухудшает результат. Применение операции XOR приводит к тому, что часть энтропии мы теряем, но гарантированно имеем результирующую энтропию не хуже максимальной энтропии слагаемых.
- У криптографов есть догма: использование генераторов псевдослучайных чисел — непростительная самонадеянность. Потому что у этих генераторов маленькая удельная энтропия. Но мы только что выяснили, что если сделать всё правильно, энтропия становится бочкой мёда, которую невозможно испортить никаким количеством дёгтя.
- Если у нас есть всего 10 байт реальной энтропии, размазанной по килобайту данных, с формальной точки зрения имеем всего 1% удельной энтропии, что очень плохо. Но если эти 10 байт размазаны качественно, и кроме брутфорса нет никакого способа эти 10 байт вычислить, всё выглядит не так уж плохо. 10 байт — это 280, и если наш брутфорс в секунду перебирает триллион вариантов, нам на то, чтобы научиться угадывать очередной знак, понадобится в среднем 19 тысяч лет.
Как было сказано выше, информационная энтропия — величина относительная. Там, где для одного субъекта удельная энтропия равна 1, для другого она вполне может быть 0. Притом тот, у кого 1, может не иметь никакой возможности узнать истинное положение дел. Системный ГСЧ выдаёт поток, неотличимый для нас от по-настоящему случайного, но на то, что он действительно случаен
для всех, мы можем только надеяться. И верить. Если паранойя подсказывает, что качество основного ГСЧ может вдруг оказаться неудовлетворительным, есть смысл подстраховаться при помощи дополнительного.
Реализация суммирующего ГСЧ на Питоне
from random import Random, SystemRandom
from random import BPF as _BPF, RECIP_BPF as _RECIP_BPF
from functools import reduce as _reduce
from operator import xor as _xor
class CompoundRandom(SystemRandom):
def __new__(cls, *sources):
"""Positional arguments must be descendants of Random"""
if not all(isinstance(src, Random) for src in sources):
raise TypeError("all the sources must be descendants of Random")
return super().__new__(cls)
def __init__(self, *sources):
"""Positional arguments must be descendants of Random"""
self.sources = sources
super().__init__()
def getrandbits(self, k):
"""getrandbits(k) -> x. Generates an int with k random bits."""
######## На самом деле всё это ради вот этой строчки:
return _reduce(_xor, (src.getrandbits(k) for src in self.sources), 0)
def random(self):
"""Get the next random number in the range [0.0, 1.0)."""
######## Не понятно, почему в SystemRandom так не сделано. Ну ладно...
return self.getrandbits(_BPF) * _RECIP_BPF
Пример использования:
>>> import random_xe # <<< Так оно называется
>>> from random import Random, SystemRandom
>>> # Создаём объект:
>>> myrandom1 = random_xe.CompoundRandom(SystemRandom(), Random())
>>> # Используем как обычный Random:
>>> myrandom1.random()
0.4092251189581082
>>> myrandom1.randint(100, 200)
186
>>> myrandom1.gauss(20, 10)
19.106991205743107
В качестве основного потока взят считающийся правильным SystemRandom, а в качестве дополнительного – стандартный ГПСЧ Random. Смысла в этом, конечно, не очень много. Стандартный ГПСЧ – точно не та добавка, ради которой всё это стоило затевать. Можно вместо этого поженить между собой два системных ГСЧ:
>>> myrandom2 = random_xe.CompoundRandom(SystemRandom(), SystemRandom())
Смысла, правда в этом ещё меньше (хотя именно такой приём почему-то рекомендует Брюс Шнайер в «Прикладной криптографии»), потому что приведённые выше выкладки справедливы только для независимых источников. Если системный ГСЧ скомпрометирован, результат также получится скомпрометированным. В принципе, полёт фантазии в деле поиска источника дополнительной энтропии ничем не ограничен (в нашем мире беспорядок встречается намного чаще, чем порядок), но в качестве простого решения предложу ГПСЧ HashRandom, также реализованный в библиотеке «random_xe».
ГПСЧ на основе потокового циклического хеширования
В простейшем случае можно взять некоторое относительно небольшое количество начальных данных (например, попросить пользователя побарабанить по клавиатуре), вычислить их хеш, а потом циклически доливать хеш на вход алгоритма хеширования и брать следующие хеши. Схематически это можно изобразить так:
Криптостойкость этого процесса основывается на двух предположениях:
- Задача восстановления исходных данных по значению хеша невыносимо сложна.
- По значению хеша невозможно восстановить внутреннее состояние хеширующего алгоритма.
Посовещавшись с внутренним параноиком, признал второе предположение лишним, и поэтому в чистовой реализации ГПСЧ схема немножко усложнена:
Теперь если злоумышленнику удалось получить значение «Хеш 1r», он не сможет вычислить следующие за ним значение «Хеш 2r», так как у него нет значения «Хеш 2h», которое он не сможет узнать, не вычислив функцию хеширования «против шерсти». Таким образом, криптостойкость этой схемы соответствует криптостойкости применяемого хеширующего алгоритма.
Пример использования:
>>> # Создаём объект, проинициализировав HashRandom лучшим в мире паролем '123':
>>> myrandom3 = random_xe.CompoundRandom(SystemRandom(), random_xe.HashRandom('123'))
>>> # Используем как обычный Random:
>>> myrandom3.random()
0.8257149881148604
По умолчанию используется алгоритм SHA-256. Если хочется чего-то другого, можно в конструктор вторым параметром передать желаемый тип алгоритма хеширования. Для примера сделаем составной ГСЧ, суммирующий в кучу следующее:
1. Системный ГСЧ (это святое).
2. Пользовательский ввод, обрабатываемый алгоритмом SHA3-512.
3. Время, затраченное на этот ввод, обрабатываемое SHA-256.
>>> from getpass import getpass
>>> from time import perf_counter
>>> from hashlib import sha3_512
# Оформим в виде функции:
>>> def super_myrandom():
t_start = perf_counter()
return random_xe.CompoundRandom(SystemRandom(),
random_xe.HashRandom(
getpass('Побарабаньте по клавиатуре:'), sha3_512),
random_xe.HashRandom(perf_counter() - t_start))
>>> myrandom4 = super_myrandom()
Побарабаньте по клавиатуре:
>>> myrandom4.random()
0.35381173716740766
Выводы:
- Если мы не уверены в своём генераторе случайных чисел, мы можем легко и потрясающе дёшево решить эту проблему.
- Решая эту проблему, сделать хуже мы не сможем. Только лучше. И это математически доказано.
- Нужно не забыть постараться сделать так, чтобы использованные источники энтропии были независимыми.
Исходники библиотеки – на
GitHub.