Ускоряем программу для 50-летнего процессора на 180000%
- среда, 15 ноября 2023 г. в 00:00:17

В прошлом году я написал программу, вычисляющую 255 цифр числа π на самом первом микропроцессоре от Intel - 4004. В той статье я упоминал рекорд ENIAC'a - 2035 цифр [^1], но побить его не смог. Настало время закрыть гештальт. В этот раз возьмём одного из преемников от Intel - 4040. Определим рамки, в которых будем разрабатывать наш код:
Основная цель это вычислить как минимум 2035 первых цифр числа π быстрее, чем это сделал ENIAC. В исходной работе с описанием данного результата [^2] озвучены 70 часов машинного времени. Значит нам нужно уложиться в 69 часов, 59 минут и 59 секунд.
Можем использовать только память, адресуемую напрямую процессором. То есть никаких внешних переключателей банков RAM/ROM.
Избегаем каких-либо предвычисленных значений, сохраненных в ПЗУ. Все вычисления должны производиться i4040. К примеру, мы не можем рассчитать таблицу логарифмов на ПК и включить её как константную секцию в код, а должны построить её на лету.
Никакой подстройки под конкретное целевое значение числа вычисляемых цифр π. Да, мы хотим вывести 2035+ цифр, но код должен корректно работать и для меньших значений.
Обратите внимание, что я структурировал статью по главам, а не хронологически. К примеру, я сначала оптимизировал функцию умножения, затем переключился на алгоритмические улучшения, но так как не достиг нужных результатов, то опять вернулся к низкоуровневым оптимизациям. А в статье работа над алгоритмом объединена в один кусок, корпение над модульным умножением - в другой, и т.д.
Несмотря на то, что 4040 вышел на несколько лет позже чем предшественник, почти все ограничения 4004 сохранились:
Тактовая частота по-прежнему 740 килогерц. Одна инструкция исполняется за 8 или 16 тактов, поэтому у нас не более 92500 инструкций в секунду.
Набор инструкций (ISA) несколько расширился, но именно что "несколько". Всё еще нет ни умножения, ни деления, ни эффективных операций с памятью. Чего уж там, даже сдвиговые инструкции отсутствуют.
Размер ОЗУ не увеличился - 1280 байт. Да-да, чуть больше килобайта. Во многих источниках указана неверная информация про меньший объём, но существовали реальные системы [^3] с 1280 байтами на борту (адресуемых напрямую, как нам и надо).
Тогда что же нам принёс полезного 4040 [^11]? Поддержку внешних прерываний, пошаговую отладку, меньшее энергопотребление в некоторых случаях, но для нашей практической задачи более интересен следующий список:
Добавились инструкции AND/OR. И это именно нововведение, потому что 4004 не имел такой роскоши. Но не всё так радужно - бинарные операции не имеют аргументов, а выполняют побитовую дизъюнкцию/конъюнкцию над конкретными регистрами. К примеру, AN6 совершает побитовое ИЛИ над регистром rr6 и аккумулятором.
Стек вызова вырос с 3-х уровней до 7. Теперь переполнение стека менее вероятно, хотя я с этим всё же столкнулся.
Регистров стало больше - 24 вместо 16. Но ISA не поменялась и 4040 имеет бинарную совместимость машинного кода с 4004. То есть индекс регистра всё еще закодирован 4-мя битами. Каким же образом мы можем адресовать дополнительные регистры? Не самым эффективным образом - переключая регистровые файлы (банки) туда-обратно с помощью инструкций SB0 / SB1
К счастью, поддерживаемый объем ПЗУ увеличился. Добавился второй банк ROM с дополнительными 4 кибибайтами. Тем не менее переключение между банками непрозрачное и требует аккуратного тайминга в коде и использования инструкций DB0 / DB1.
Давайте рассмотрим какие варианты у нас есть:
Краниковый алгоритм [^4]. Я описывал его в прошлой статье. Если вкратце, то алгоритм работает с массивом цифр, хранимых в ОЗУ. Размер этого массива пропорционален количеству вычисляемых цифр. Нам просто не хватит RAM для 2000+ цифр.
Формулы Мэчина. С вычислительной точки зрения вполне нас устраивают, но даже для таких простых формул нам не хватит памяти. Дело в том, что нам нужно хранить как минимум два длинных числа (разрядностью не менее чем целевое количество вычисляемых цифр π). Никак не упаковать 4000+ цифр в 1280 байт.
Улучшенный краниковый алгоритм [^5]. В нём не используется какой-либо массив, но, так же как и в формулах Мэчина, мы работаем с весьма длинными числами. Даже для 255 цифр необходимый объем памяти уже 7 кибибайт.
Формула от Bailey–Borwein–Plouffe [^6]. Весьма интересная идея, но по этой формуле мы получаем число π в 16-ричной или 2-чной системах счисления. Я всё же ориентирован на 10-ричную.
Алгоритм Плуффа [^7]. Очень медленный. С такой асимптотикой будет очень сложно уложиться в заданной время (скорее всего и невозможно).
Алгоритм от Фабриса Беллара, вдохновенный работой Плуффа [^8]. Не самый быстрый, но относительно простой и не требующий сложной математики.
Алгоритм Ксавье Гурдона [^9]. Очень быстрый, но весьма сложный и объемный. Для его реализации скорее всего не хватит ПЗУ, ведь у нас вся программа не может превышать объема в 8000 инструкций, а нам придётся написать все базовые математические функции.
Судя по всему, оптимальнее будет взять работу Беллара за основу. Для начала посмотрим как работает его алгоритм.
Плуфф (а затем и Беллар) используют весьма занятную формулу для π:
Вывод этой формулы (как и несколько других увлекательных равенств) можно найти в статье Лемера. [^10]
Нотация в виде круглых скобок описывает центральный биномиальный коэффициент и может быть раскрыта таким образом:
Получаем окончательную форму числового ряда, с которым будем работать:
Начнём с упрощеннго примера. Пусть у нас есть дробь и мы хотим узнать цифру на позиции
этого числа. Как мы это можем сделать?
Для начала запишем факторизацию :
Затем определим несколько переменных:
После применения китайской теоремы об остатках мы получим:
Введём еще одну переменную :
Так как, то мы можем использовать эту подстановку для вычисления дробной части
:
Возможно, тождество (1) очевидно, но для полноты статьи приведу небольшое доказательство:
Теперь мы можем записать формулу для вычисления цифр числа с позиции
:
Переход (2) нужен только для упрощения вычислений: мы стараемся избежать больших чисел (а может быть весьма большим числом). И так как мы ищем только дробную часть числа, то можем перейти к сложению остатков и модульной арифметике.
Можно заметить, что формула не рекуррентна: каждый член суммы может быть вычислен независимо от прошлых. А значит нам нет нужды хранить весь ряд, достаточно только работать с промежуточным значением. Кроме того, использование модульной арифметики позволяет нам оперировать с числами весьма скромной разрядности и пары десятков байт будет достаточно для вычислений.
Формула для π это не просто дробь, а числовой ряд. Значит нам нужно адаптировать наши выкладки к числу, записанному в форме частичной суммы положительного конечного ряда. Дополнительно уточним, что кратность простых множителей в разложении знаменателя может быть больше 1.
Пусть будет множеством простых чисел, которые встречаются в разложении
для какого-либо
. При этом для пары
кратность простого числа
в факторизации
может быть 0 (это конкретное число не является множителем конкретного
). Также объявим
- максимальная кратность для
среди всех разложений
. Суммируя все вводные, можем определить числовой ряд:
По схеме из прошлого раздела, объявим несколько переменных:
И. применяя китайскую теорему об остатках, получаем выражения для отдельного члена ряда и для частичной суммы ряда:
Следующим шагом перейдём к использованию общего делителя , который не зависит от
:
Применяем тот же трюк, что и для дробей - так как целая часть нас не интересует, то мы можем использовать не такие большие числа из класса вычетов по модулю .
Важное наблюдение - мы можем заметить, что так же принадлежит к тому же классу вычетов по модулю
. Это не столь очевидно, но сейчас мы это покажем, используя упрощенный пример:
Видно, что мы два выражения эквивалентны, и значит мы можем записать финальное выражение для :
Наконец, формула для цифр частичной суммы ряда почти идентична формуле из прошлого раздела:
Мы можем записать значения ,
и
для формулы π:
Функция - степень вхождения простого числа
в разложение
.
Пара моментов, которые стоит упомянуть: вынесли из
не из-за каких-то математических соображений, а для упрощения алгоритма. Также мы сразу сокращаем общий множитель для
и
.
Мы определили почти все переменные, которые нам нужны, за исключением . У нас была вводная, что
не является множителем
, но это не так для нашей формулы, ибо
очевидно имеет в множителях
. К счастью, это имеет влияние только на значание
. Для нашей формулы мы можем записать степень вхождения
как:
Раскроем двойной факториал и используем формулу Лежандра:
В (3) мы просто исключили потому что этот член делится только на 2, а среди
у нас нет 2 (
по определнию двойного факториала имеет только нечётные множители), а значит он никак не влияет на функцию кратности. Теперь взглянем на каждый член суммы и отметим, что он равен либо 0, либо 1:
Так как и, даже если каждый член суммы будет равен 1, то максимальное значение суммы будет огранично сверху
.
Следующий вопрос заключается в том, какое же значение верхней границы суммирования () будет достаточным, чтобы получить цифры числа, с определённой позиции. Если формализовать наш запрос, то в виде неравенства он будет выглядеть как-то так:
Умножая на , мы сдвигаем десятичную точку на
позиций вправо. Цифры слева от точки уже более-менее корректны, и значит сильное увеличение
не будет оказывать влияния на них, и можно принять их за финальные. Поэтому находим с какого
целая часть произведения примерно определена, и добавляем некоторый
в качестве запаса на точность.
Чтобы решить это неравенство, используем другую формулу центрального биномиального коэффициента:
Трансформируем числовой ряд π, используя формулу выше:
Исследуем часть этого выражения и определим его границы:
Исходя из определения двойного факториала, достаточно очевидно почему у нас есть верхняя граница в виде , когда
. Теперь вернёмся к основному неравенству (заменив кусочек сверху на
):
Проведя серию нехитрых импликаций, получим искомую оценку для :
Можно, конечно, продожить, но так как это всё равно только приблизительное число и мы в любом случае будем добавлять какой-то для обеспечения точности вычислений, то можно просто докинуть
к этому
. Для наших не таких грандиозных целей (
),
может быть весьма небольшим. Я остановился на 70.
Крутим два цикла: внешний цикл по простым числам (), а внутренний служит для вычисления
. Сразу же на уровне алгоритма закладываем небольшую оптимизацию - вместо вычисления факториалов на каждом шаге цикла, мы можем использовать реккурентные формулы:
и
. Кроме этого, мы сразу делим
и
на текущее простое число
и одновременно обновляем значения
и
, которые будут использоваться для возведения
в нужную степень.
Прежде чем начать писать код на ассемблере, я разработал референсную версию алгоритма на JS:
const getNinePiDigits = (n) => {
const N = Math.trunc((n + 20) * Math.log(10) / Math.log(2));
let digits = 0;
for (const a of primes.filter((prime) => prime > 2 && prime < 2 * N)) {
const vmax = Math.trunc(Math.log(2 * N) / Math.log(a));
const m = a ** vmax;
let f = 0, A = 1, b = 1, v = 0, u = 0;
for (let k = 2; k <= N; k++) {
b = (b * (k / (a ** multiplicity(a, k)))) % m;
A = (A * ((2 * k - 1) / (a ** multiplicity(a, 2 * k - 1)))) % m;
u += multiplicity(a, k);
v += multiplicity(a, 2 * k - 1);
if (v - u > 0) {
f = (f + (k * b * modularInverse(A, m) * (a ** (vmax - v + u)))) % m;
}
}
d = (f * modularPower(10, n, m)) % m;
digits = (digits + (d / m)) % 1;
}
return Math.trunc(digits * 1e9).toString().padStart(9, '0');
};
Для более-менее простых програм (таких как прошлый проект) мне не требовалось что-то большее, чем простой компилятор ассемблера в машинный код. Но разработка текущего проекта становилась всё сложнее. Так что мне пришлось расширить набор инструментов.
От препроцессора я хотел получить две возможности:
поддержка модульности - до этого весь код содержался в одном файле
примитивные макросы
К примеру, есть у нас модуль, который реализует функцию foo (foo.i4040):
%define FOO_PARAM1_VAL1 0x5
%define FOO_PARAM1_VAL2 0xA
%define FOO_PARAM2_VAL1 D
foo:
...
BBL 0
А в другом модуле мы хотим использовать эту функцию:
%include "foo.i4040"
bar:
FIM r0, $FOO_PARAM1_VAL1 . $FOO_PARAM2_VAL1
JMS foo
FIM r0, $FOO_PARAM1_VAL2 . 0
JMS foo
BBL 0
Макросы оказались очень удобны для работы с переменными в памяти. Я несколько раз пересматривал структуру размещения переменных в RAM (скажем, переменная, в которой хранилось значение , могла сменить регистр RAM с #5 на #9). Без этой фичи, мне бы пришлось искать в исходном коде конкретное число и думать о том, относится ли оно к операции с памятью или просто константа.
Первая версия компилятора была бесхитростной - берём инструкции одну за одной, транслируем их в машинный код и записываем в итоговый образ ПЗУ. Заключительным этапом подставляем конкретные адреса в инструкции перехода по меткам. Мы не могли сделать этого при первом проходе, потому что метка могла быть объявлена позже, чем инструкция перехода, которая ссылается на эту метку. Однако архитектура 4004/4040 имеет несколько особенностей связанных с переходами и структурой машинного кода:
Некоторые команды перехода могут работать с адресами, только внутри той же страницы ПЗУ (размером 0x100 байт), где и размещена сама инструкция. Например, инструкция по адресу 0x2AA может совершить переход на 0x255, но не на 0x655.
Такие короткие переходы имеют ещё одну особенность - если они расположены на последних байтах страницы ПЗУ, то переход будет выполнен не на адрес внутри страницы с этой инструкцией, а на адрес со следующей страницы. Инструкция по адресу 0x7FF или 0x7FE, выполняющая короткий переход на адрес 0x7BB неожидано передаст управление на 0x8BB.
Изначально я исправлял конфликты такого рода (когда инструкция короткого перехода находилась на одной странице ROM, но ссылалась на адрес в другой странице) вручную, жонглируя участками кода, либо просто добавлял сериюNOP в качестве заплаток для проблемных функций. Какое-то время это работало, но код становился всё объемнее и объемнее, и в определённый момент подготовка исходника для успешной компиляции превратилась в кошмар.
Кроме того, накопилось еще несколько пожеланий к компилятору:
Поддержка двух банков ПЗУ. Программа разбухала, и я опасался, что не уложусь в 4 КиБ.
Необходимость размещения кода по конкретным адресам.
Остановлюсь на этих требованиях подробнее.
Как я уже ранее упоминал, переход между банками ROM не совсем прозрачен для программиста, и требуется самостоятельно переключаться между ними:
__location(0x0:0x00)
entrypoint:
JMS output
DB1
JMS foo
HLT
output:
LDM 0xF
WMP
BBL 0
__rom_bank(0x1)
foo:
JMS output
DB0
NOP
BBL 0
В этом листинге можно наблюдать следующее:
entrypoint располагается в первом банке, по адресу 0x000. И отсюда процессор начинает исполнять код после сигнала сброса.
foo будет размещен во втором банке по адресу, который выберет компоновщик.
функция output используется кодом в обоих банках, а значит необходимо её продублировать.
инструкция NOP перед командой возврата BBL необходима для соблюдения нужных таймингов. DBx переключает банк ПЗУ через 2 цикла, так как предполагается использование этой инструкции в связке с командами перехода, которые как раз и исполняются за 2 командных цикла. В отличии от них, BBL занимает только один цикл, так что нам нужно потратить дополнительный цикл для корректного перехода в нужный банк во время возврата из функции.
Мы хотим задавать конкретный адрес размещения кода не только для точки входа, но и для целей оптимизации - создания эффективных таблиц перехода. В ISA присутствует инструкция косвенного переходаJIN rX , которая передаёт управление на адрес, содержащийся в регистровой паре (8-бит). С помощью этой команды я могу переходить на участки кода в зависимости от значения регистра, избежав кучи сравнений. Я активно использовал этот трюк. Вот, к примеру, функция для деления 4-битного числа на 4-битное число. Здесь для каждого значения делителя (1..15) у меня свой блок кода.
__location(00:0x10)
div4x4_1:
XCH rr12
LDM 0x0
XCH rr13
BBL 0
# INPUT:
# acc - dividend
# rr10 - divisor
# rr11 - 0x0
# OUTPUT:
# rr12 - quotient
# rr13 - reminder
__location(00:0x18)
div4x4:
JIN r5
__location(00:0x20)
div4x4_2:
RAR
XCH rr12
TCC
XCH rr13
BBL 0
...Определившись с необходимостью более изощренной компиляции, я составил такой конвейер превращения исходного кода в образ ROM:
Препроцессор
Парсинг исходного кода с использованием простой грамматики. В качестве результата парсинга выступает массив инструкций с представлением команд в виде машинного кода и некоторых служебных данных таких как позиция команды в исходном коде (номер строки) и информация о ссылках на другие участки кода.
Объединение отдельных команд в связанные блоки. Блоком не всегда является вся функция целиком. Даже если инструкции семантически принадлежат к одной функции, они всё равно могут быть разбросаны по всему образу ROM, если это будет нужно компоновщику. Блоком в данном случае я называю набор инструкций, которые будут исполняться последовательно. Команды безусловных переходов или возврата завершают блок.
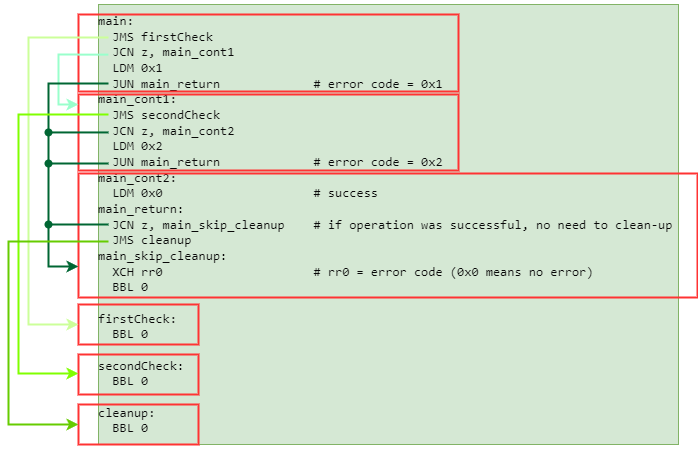
На этом этапе у нас есть список блоков и информация о их связях между собой. Теперь можем сформировать более крупные структуры - объединения блоков. Это набор блоков, связанных между собой короткими переходами. Необходимо их рассматривать вместе из-за ограниченний с короткими переходами, описанных выше. Тогда как блоки, ссылающиеся через длинные переходы, могут располагаться в произвольных местах относительно друг друга. К сожалению, мы не можем применить какой-нибудь алгоритм, решающий классическую задачу об упаковке в контейнеры, потому что наши объединения блоков могут пересекать страничную границу ROM, даже несмотря на наличие коротких переходов:
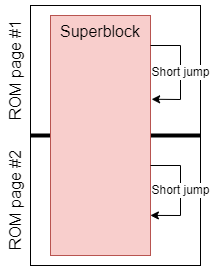
Поэтому я пошёл по более прямолинейному пути - завёл курсор, который указывает на текущую незаполненную позицию в ROM, и который мы двигаем в направлении конца образа. На каждом шаге я пытаюсь вставить какой-либо супер-блок на позицию, заданную курсором, отдавая приоритет наиболее крупным объединениям. Если никакой супер-блок не может быть размещён (скажем, нарушаются внутренние короткие переходы), то двигаем курсор на 1 байт вперёд и опять проверяем оставшиеся блоки.
Блоки, для которых мы указали конкретную позицию, не нуждаются в какой-либо дополнительной обработке компоновщиком. Он их просто вставляет по нужному адресу. Несмотря на то, что основной алгоритм размещения блоков линейно двигает курсор вперёд, я добавил небольшую оптимизацию и стараюсь воткнуть мелкие блоки в свободное пространство между участками кода на фиксированных позициях.
Дополнительное усложнение связано с тем, что мы можем тасовать блоки внутри объединения в поисках варианта, который позволит разместить их по текущему адресу. А одно объединение может содержать весьма большое количество блоков - больше десятка. И количество перестановок у нас будет . Поэтому чтоб не усложнять примитивный алгоритм, я просто-напросто добавил в компоновщик кэш - ключём кэширования является суперблок (какой-нибудь хэш, который зависит от сгенерированного машинного кода), а в качестве значения выступает список смещений внутри страницы ПЗУ и информацией о том, можно ли по данному смещению разместить этот суперблок или нет.
Не секрет, что отладка и тестирование программ занимают большую часть времени при разработке, а отлаживать код на реальном железе не очень удобно. Я уже писал эмулятор для i4004 и GUI к нему, но потребовался новый функционал:
Хотелось запускать эмулятор не только в браузере, но и иметь программный интерфейс для использования в автоматических тестах.
Адаптация эмулятора под 4040: новые инструкции, расширенный набор регистров, дополнительный банк ПЗУ.
Поддержка снимков ОЗУ. Некоторые функции нашей программы ожидают определенное состояние памяти, поэтому для их тестирования (как автоматического, так и через GUI) нужна возможность указывать начальный снимок RAM.
Профилирование. Без этого мы можем только гадать, что является узким местом нашей программы. При эмуляции мы можем составлять профили на уровне команд, но такая детализация мне была не нужна, и я остановился на уровне функций.
Так как мы добавили компоновщик, то мы потеряли прямое отображение исходного кода в машинный код образа ROM. Раньше мы могли относительно просто транслировать номер строки исходного кода в адрес в ПЗУ. Теперь же требуется поддержка карт кода (source maps) в GUI эмулятора.
Эмулятор уже поддерживал точки останова, но я добавил ещё один полезный инструмент отладки - отображение значения переменных в читаемом виде. Многие переменные являются 16-битными числами. Иногда они хранятся в регистрах, и бывало не так удобно, глядя на список регистров, считывать значение переменной. Или другой пример - переменная может храниться в ОЗУ. Но, имея полную карту памяти перед глазами, не так просто вычленить интересующие ячейки. Особенно, если нужно следить за несколькими переменными.
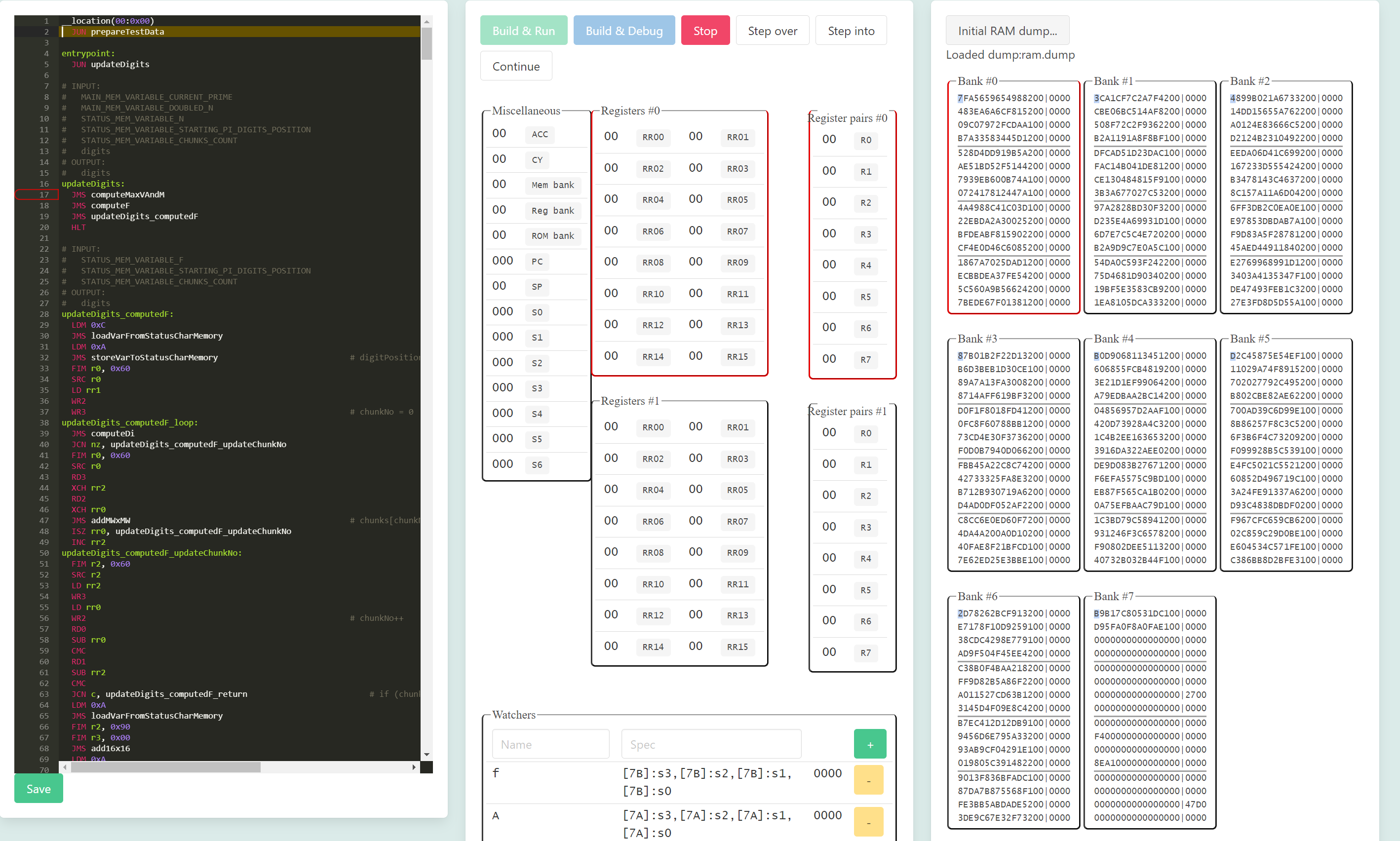
Если честно, то к задаче я подошёл расслабленно. 70 часов? Звучит несложно. Поэтому я написал относительно простой код без каких-либо оптимизаций. Тем не менее, стоит упомянуть общие рассуждения, которые пригодились в дальнейшем.
Прежде всего требовалось понять, какой разрядности у нас числа. От этого зависит и используемые алгоритмы примитивных функций, и организация памяти. Мы ограничили искомое количество цифр π () верхней границей в 2043, значит
у нас не более 7000, а модуль
меньше 14000. Следовательно большинство операций будут над 14-битными числами. Конечно же, мы не будем работать с половиной машинного слова и выровняем нашу разрядность по машинному слову (4 бит). То есть, в основном у нас будут 16-битные переменные.
Напомню о том, как выглядит RAM в системах с Intel 40xx. У нас доступно до 8 банков памяти, каждый банк содержит 16 регистров, состоящих из двух частей: 16 основных 4-битных символа и 4 статусных 4-битных символа. Основное различие между этими двумя категориями заключается в том, как мы получаем к ним доступ.
Пример работы с основными символами:
FIM r0, 0xF0 # loads 0xF0 to r0
SRC r0 # selects register F and main character 0
RDM # loads the selected main character to the accumulator
XCH rr2 # rr2 = accumulator
FIM r0, 0xF1 # loads 0xF1 to r0
SRC r0 # selects register F and main character 1
RDM # loads the selected main character to the accumulator
ADD rr2 # accumulator = main character 0 + main character 1А вот к статусным символам мы можем обращаться через специальные инструкции RDx / WRx, без необходимости предварительно передавать номер символа микросхеме RAM.
FIM r0, 0xF0 # loads 0xF0 to r0
SRC r0 # selects register F and main character 0
RD0 # loads status character 0 to the accumulator
XCH rr2 # rr2 = accumulator
RD1 # loads status character 1 to the accumulator
ADD rr2 # accumulator = status character 0 + status character 1Как видите, взаимодействие со статусными символами обычно быстрее, чем с основным набором. А так как их всего 4, то нам повезло уложиться в 16 бит и мы сможем разместить переменные в более "быстрой" памяти.
Зная верхние границы для , мы можем также подумать о способе хранения списка простых чисел. Логично получить их только один раз, а не находить их перед каждой новой пачкой цифр π. Примерное количество простых чисел, меньших
составляет 2000. Просто записать их все в память не получится, но мы можем хранить их в виде битовой карты: если бит на позиции
установлен в 1, это будет значить, что
- простое число. Нам доступно 10240 бит в RAM, тогда как нам нужны числа до 14000 (верхняя граница для
), но мы можем схитрить - мы знаем, что чётные числа не являются простыми (за исключением 2), и поэтому можем исключить их из нашей битовой карты. Таким образом, вместо 14000 бит нам требуется только 7000.
Для получения простых чисел используем стандартное решето Эратосфена.
Другая тема на подумать - логарифмы. Мне нужно знать значение для вычисления
. Как вы уже поняли, вычисление логарифма это не такая простая задача для 4040. Конечно же, можно просто использовать предвычисленную константу, но это не укладывается в наши правила. Вместо этого, можем использовать апроксимированное значение:
. Нам должно этого хватить, так как нам не так важно точное значение, лишь бы оно было не слишком маленьким.
Ещё один нужный нам логарифм это . Но, к счастью, нас интересует только целая часть логарифма, поэтому можем использовать простой цикл
.
Процессор не поддерживает числа с плавающей точкой из коробки, но по алгоритму должен содержать дробную часть числа. Дабы не реализовывать арифметику чисел с плавающей точкой самостоятельно, я избрал другой путь - будем работать с фиксированной точкой: 1 машинное слово на целую часть и 15 слов на дробную. Наша функция получения цифр π выдаёт по 9 цифр за раз, но еще 6 разрядов необходимо для избежания накопительной погрешности округления.
Возиться с длинной арифметикой не хотелось, поэтому я и отбраковал наиболее навный подход: производим операцию (умножение/возведение в степень), а уже затем результат приводим по модулю . Сразу реализовал бинарный подход к вычислению произведения и возведения в степень.
Нам известно мультипликативное свойство модульной арифметики:
Поэтому мы можем записать такое рекурсивное определение функции модульного умножения :
Похожая идея используется и для модульного возведения в степень:
Последняя нетривиальная модульная операция это получение обратного числа по модулю. Однако, мы знаем что и
являются взаимопростыми и поэтому мы можем использовать теорему Эйлера:
Так как , то значение функции Эйлера для
вычисляется на раз-два:
Насколько мы близки к нашим заветным 70 часам? Увы, очень и очень далеки от них. Я даже не дождался окончания эмуляции, но я использовал полиномиальную аппроксимацию после первых 800 цифр для получения примерной оценки. И увидел ужасающие 14.5 лет. Что ж, видимо намечается весьма долгое и интересное приключение по улучшению производительности...
Прежде чем погружаться в дебри низкоуровневых оптимизаций, я решил поизучать алгоритм более внимательно. Особых чаяний я не питал, ибо Фабрис Беллар очень талантливый программист и математик, и шансы, что он пропустил какой-то очевидный трюк, я оценивал невысоко. Но, тем не менее, он решал немного другую задачу - найти цифру на n-ой позиции в числе π, тогда как я старался найти n цифр числа π. Возможно мы сумеем переиспользовать какие-то вычисления между вызовами основной функции? В памяти мы не можем держать большой кэш - всего порядка 300 записей с 16-битными ключами и значениями. Нужно думать сильнее.
В какой-то момент я осознал, что раз при вычислении мы можем совершить больше итераций, чем минимально необходимо, и это не приведёт к неправильному результату, то значит есть возможность вычислить
для наибольшего
и использовать его для более старших разрядов π (меньших
). Конкретная позиция вычисляемой пачки цифр (
) будет использоваться только во внешнем цикле по простым числам.
В изначальном раскладе мы всё равно будем вычислять для максимального
, так что это не является дополнительной работой. Да, мы потратим время на ненужные вычисления
для
, но зато мы крутим ресурснозатратный внутренний цикл только для
.
Как обсуждалось выше, хранится как 16-разрядное число, а значит нам нужно 8 байт под него. Если мы хотим проходить внешний цикл по простым числам только один раз и обновлять
сразу для всех позиций цифр в π, то нам нужно 1824 байт только под промежуточные значения для
. Мы получаем по 9 цифр для заданного
, значит для 2048 цифр будем заводить 228 разных значений для
- 0, 9, 18, ... А 228 * 8 байт и дают нам требуемые 1824 байт. Это превышает весь доступный объём памяти. Но мы просто разделим всю работу на два прохода - выдадим цифры с позиций [0, 1026], а затем с [1026, 2052]. Тогда потребуется в 2 раза меньше памяти - 912 байт, что, по крайней мере, укладывается в физические ограничения системы.
Код для референсной реализации изменился незначительно:
for (let i = 0; i < digits.length; i++) {
d = (f * modularPower(10, startingPosition + i * 9, m)) % m;
digits[i] = (digits[i] + (d / m)) % 1;
}После адаптации версии на ассемблере, я получил впечатляющее ускорение в 85 раз, и программа финиширует за 64 дня вместо нескольких лет. Но нам всё ещё осталось улучшить это время в 20 раз!
Большая часть памяти теперь отведена под, но у нас же там лежит битовая карта простых чисел. Как же всё это уместить вместе?
Всё просто - вместо обычного решета Эратосфена будем использовать сегментированное. У нас будет начальный сегмент простых чисел меньших (обозначим это значение как длина сегмента). Кроме этого, заведём текущий рабочий сегмент той же длины, и по надобности мы будем его обновлять, используя начальный сегмент.
Произведём оценку требуемой памяти. Длина сегмента у нас 118, а значит мы можем прикинуть, сколько займёт начальный сегмент. Каждое простое число в этом сегменте укладывается в 1 байт, и всего у нас около 30 простых чисел, меньших 118. Следовательно, нам хватит всего 30 байт под начальные данные.
По определению, разница между первым и последним числами в текущем сегменте не превышает длину сегмента. Значит, мы можем организовать хранение теущего сегмента в весьма компактной манере - 16-битная переменная в качестве наименьшего простого числа в сегменте и битовая карта на 59 записей (нам по-прежнему не нужны чётные числа). Таким образом, даже если вместо отдельных битов мы будем использовать целые машинные слова, то нам потребуется всего 32 байта.
Мы не используем BCD формат для (в этом формате, к примеру, число
1234 будет записано в памяти 0x1234 , а не как 0x4D2) потому что он более раздут. А значит десятичная точка для дробных чисел проигрывает шестнадцатеричной. Можно сказать, что в хранилось число, умноженное на
, а мы меняем этот множитель на
.
Я не слишком верил в то, что только оптимизации кода хватит для достижения нужного результата. Алгоритмические улучшения практически всегда должны идти первым номером, когда не хватает производительности. Поэтому я продолжил исследовать алгоритм. И вскорости подметил, что для простых чисел превышающих , их кратность в
всегда будет не больше 1 (
). Следовательно, мы можем упростить кое-какие вычисления.
Значение имеет бинарную природу и чередуется между 0 и 1. И мы даже можем вычислить периоды чередования:
начинает иметь значение 1, когда
, а возвращается к 0 при
. Приведу простую визуализацию такого чередования:

Код стал немного менее читабельным, но зато быстрее.
do {
// iterate until next k, that satisfies (2 * k - 1) % a === 0
for (; (2 * k - 1) % a !== 0; k++) {
b = (b * k) % a;
A = (A * (2 * k - 1)) % a;
}
// v becomes 1 here
b = (b * k) % a;
A = (A * ((2 * k - 1) / a)) % a;
f = (f + modularInverse(A, a) * b * k) % a;
k++;
// iterate until next k, that satisfies k % a === 0
for (; (k % a) !== 0; k++) {
b = (b * k) % a;
A = (A * (2 * k - 1)) % a;
f = (f + modularInverse(A, a) * b * k) % a;
}
// now v becomes 0
b = (b * (k / a)) % a;
A = (A * (2 * k - 1)) % a;
k++;
} while (k <= N);В нём мы исключили возведение в степнь и несколько ненужных сравнений, но есть еще простор для улучшений:
Деление тоже оказывается ненужным. Если внимательно присмотреться к циклу, то шагом цикла является текущее простое число . Поэтому мы знаем что внутри цикла значения
k / aи (2 * k - 1) / a на каждой итерации цикла увеличиваются на 1 и на 2, соответственно. Целочисленное деление заменяем простым сложением.
Мы можем держать множители для и
уже в виде вычетов по модулю
. Тогда при модульном умножении нам будет меньше работы.
В начале тела внешнего цикла у нас есть под-цикл для случая, когда . И мы знаем, что перед началом исполнения этого под-цикла
, следовательно у нас есть известная последовательность умножений:
, которая всегда одна и та же на каждой итерации внешнего цикла, поэтому вычисляем этот коэффициент один раз до входа в цикл:
Делаем референсный код еще менее читабельным.
let multiplierForZeroV = factorial(((a - 1) / 2) + 1) % a;
let k = ((a - 1) / 2) + 1;
let reducedCoefA = 3;
do {
// iterate until next k, that satisfies (2 * k - 1) % a === 0
for (reducedCoefB = 2; reducedCoefB <= (a - 1) / 2; reducedCoefB++) {
A = (A * reducedCoefA) % a, reducedCoefA += 2;
}
b = (b * multiplierForZeroV) % a;
// v becomes 1 here
A = (A * multiplierA) % a, multiplierA += 2;
f = (f + modularInverse(A, a) * b * reducedCoefB) % a;
k++, reducedCoefB++;
// iterate until next k, that satisfies k % a === 0
reducedCoefA = 2;
for (; reducedCoefB < a; k++, reducedCoefB++) {
A = (A * reducedCoefA) % a, reducedCoefA += 2;
b = (b * reducedCoefB) % a;
f = (f + modularInverse(A, a) * b * reducedCoefB) % a;
}
// have a check of the loop boundary now to avoid redundant first loop
k += (a + 1) / 2;
// now v becomes 0
b = (b * multiplierB) % a, multiplierB++;
A = (A * reducedCoefA) % a, reducedCoefA += 2;
// try to keep the factor lower than "a"
if (reducedCoefA > a) {
// factor is incremented by 2, so it could be bigger than "a" just by 1
reducedCoefA = 1;
} else {
A = (A * reducedCoefA) % a;
reducedCoefA += 2;
}
} while (k <= N);Это было весьма интересное наблюдение, но в итоге производительность возросла только на десятки процентов, в то время как я нуждался в тысячах. Что же, давайте переключаться на оптимизацию отдельных базовых функций.
Обычно, если возникают проблемы с производительностью, то необходимо найти узкое горлышко и горячие участки кода. Адаптировал свой профайлер для выдачи трасс, поддерживаемых утилитой flamegraph и получил следующий результат:

После получения флеймграфа, сразу стало очевидно, какая же операция является узким местом. Судя по всему, "быстрая" реализация, основанная на теореме Эйлера, оказалась не такой уж и быстрой. Набросал вариант с использованием расширенного алгоритма Евклида и получил весьма обнадеживающие цифры. А затем я вспомнил про бинарную версию этого же алгоритма. Как обычно, перед написанием кода на ассемблере, я реализовал алгоритм на языке высокого уровня:
const modularInverse = (a, m) => {
if (a === 1) {
return 1;
}
let rx = a, ry = m;
let v = 1, u = 0;
while (rx % 2 === 0) {
rx = rx >> 1;
v = (v % 2 === 0) ? (v >> 1) : (v + m) >> 1;
}
while (ry > 1) {
if (ry % 2 === 0) {
ry = ry >> 1;
} else {
if (ry < rx) {
[rx, ry] = [ry, rx];
[v, u] = [u, v];
}
ry = (ry - rx) >> 1;
u = (u - v) % m;
}
u = (u % 2 === 0) ? (u >> 1) : ((u + m) >> 1);
}
return u < 0 ? (u + m) : u;
}Перевод данного фрагмента на ассемблер прошёл весьма просто. Единственное, на что можно обратить внимание это то, как производится знаковая операция сдвига (только функция получения обратного оперирует отрицательными числами). На удивление, получилось весьма лаконично:
LD rr3 # load highest word of number
RAL # put sign bit to carry to be able to shift negative numbers
LD rr3 # again load the highest word of the number
RAR # shift it right, but because carry stores sign a bit
# it would be propagated back to the highest bit of word
XCH rr3 # save updated wordСуществуют еще более шустрые варианты реализации этой операции, но мне не пришлось их внедрять.
Возводить в степень нам нужно в двух случаях: 1) для вычисления
и 2) вычисление
.
Мы знаем что пробегает от 0 до заданного
с шагом цикла в 9, следовательно мы можем не вычислять
каждый раз, а завести переменную, и на каждой итерации умножать её на
. Так мы заменяем возведение в степень тремя умножениями (наши функции работают с 16-битными числами, поэтому мы не можем умножить число на
за один вызов функции умножения):
let powered10 = modularPower(10, startingPosition, m);
for (let i = 0; i < digits.length; i++) {
const d = (powered10 * f) % m;
digits[i] = (digits[i] + (d / m)) % 1;
powered10 = (powered10 * 1000 * 1000 * 1000) % m;
}Второй случай актуален для .
Если посмотрим на ограничение сверху: , то нетрудно заметить, что степень, в которую мы возводим, не превосходит 7. Кроме того
, а значит нам не требуется модульное возведение в степень, достаточно будет обычного.
У нас всего 7 значений , так что не трудно будет их вычислить заранее и записать в небольшое кэш в памяти. Уж 14 байт-то найдём на это.
Таким образом мы совсем избавляемся от модульного возведения в степень.
После обновления алгоритма и отделения ветви кода со случаем , у нас осталось не так уж и много операций деления. Тем не менее, если мы можем их оптимизировать, то почему бы и нет?
Даже если у нас нет задачи делить 4-битные числа, то всё равно эта операция является базой для длинного деления. Простое вычитание в цикле оказалось не таким уж и медленным и занимало 17 циклов в среднем (для всех комбинаций 4-битного делителя и делимого):
div4x4:
FIM r6, 0x00
div4x4_loop:
SUB rr11
JCN nc, div4x4_return
CLC
ISZ rr12, div4x4_loop
div4x4_return:
ADD rr11
XCH rr13
CLC
BBL 0В главе про компилятор и компоновщик, я уже упоминал подход с 15 специализированными функциями деления, каждая из которых реализует деление на конкретное число от 1 до 15. Размер такой специализированной функции не может превышать 16 байт, потому что они располагаются по фиксированным адресам 0x10, 0x20, 0x30, ... Для некоторых делителей было невозможно уложиться в данные рамки, но так как у нас был некий общий код, используемый в нескольких блоках и код функций содержал условные переходы, то я смог упаковать код для всех случаев в одну страницу ROM не тратя циклы на сшивание разных участков между собой.
Среднее значение циклов на один вызов операции деления уменьшилось до 11. Казалось бы, 6 циклов не так много, но в относительном выражении это 35% ускорение для этой небольшой функции.
Другая базовая операция, которая используется повсеместно, в том числе и для длинного деления - это умножение 4-битных чисел в 8-битное произведение. Если наивная версия 4-битного деления уже была относительно быстра до начала оптимизации, то мы не можем сказать того же самого про первую версию операции умножения. Серия сложений одного из множителей в цикле с количеством итераций, заданным другим множителем, показала себя не очень эффективно - около 70 циклов в среднем.
Для выправления ситуации воспользуемся тем же подходом, что и в прошлом разделе. Но придётся еще всё же заиметь таблицу умножения в ОЗУ. Мы можем сократить использование памяти под эту таблицу, написав быстрые функции умножения на 0, 1, 2 и 8. Умножение числа на 2 и 8 можно сделать через сдвиговые операции. Для всех остальных множителей мы обращаемся к памяти.
__location(01:0x00)
mul4x4_0:
FIM r6, 0x00 # low, high = 0
BBL $BANK_WITH_VARIABLES
# INPUT:
# acc - first factor (a)
# rr10 - second factor (b)
# rr11 - 0x0
# OUTPUT:
# rr12 - low word of product
# rr13 - high word of product
__location(01:0x08)
mul4x4:
JIN r5
__location(01:0x10)
mul4x4_1:
XCH rr12 # low = a
LDM 0x0
XCH rr13 # high = 0
BBL $BANK_WITH_VARIABLES
__location(01:0x20)
mul4x4_2:
RAL
XCH rr12
TCC
XCH rr13
BBL $BANK_WITH_VARIABLES
__location(01:0x30)
mul4x4_3:
XCH rr12
LDM $BANK_WITH_MUL_TABLE_FOR_FACTOR_3
DCL
SRC r6
RD2
XCH rr12 # low
RD3
XCH rr13 # high
BBL $BANK_WITH_VARIABLESСуществует известный алгоритм длинного деления от Кнута [^12], но он весьма обобщенный - вместо этого мы можем написать несколько разных вариаций деления в зависимости от разрядности делителя и делимого. К примеру, вариант функции для деления 12-битного делимого на 8-битный делитель, или 8-битное делимое и 4-битный делитель, и так далее. Всего у нас 10 таких комбинаций (делитель всегда имеет меньшую разрядность чем делимое) и только для 3х из них нам требуется написать реализацию алгоритма D: 16x12, 16x8 и 12x8. Для всех других случаев мы можем разработать более быстрый код.
После всех улучшений из прошлых глав, операция модульного умножения стала наиболее горячей функцией в коде - занимает 60% всего времени исполнения программы. Поэтому я потратил весьма много времени, оттачивая код умножения. Некоторые оптимизации остались в конечной версии программы, некоторые заменились более эффективными вариантами.
У меня было искушение использовать алгоритм Монтгомери для модульного умножения, причём мы можем держать числа в форме Монтгомери довольно долго - вернуться к нормальной форме нужно будет только перед вычислением . Однако прикинул, что этот алгоритм включает в себя 3 обычных умножения 16-битных чисел (4 разряда,
), и даже со всеми оптимизациями нам потребуется
умножений с 4-битными операндами [^13]. Легко посчитать - 30 умножений и каждое требует как минимум 12 циклов, а значит мы потратим 360 циклов только на умножение, а еще не забываем про 150 операций сложения (формула есть в статье выше). Слишком долго.
Ок, а что насчёт обычного длинного умножения с последующим приведением произведения по модулю? Основная операция ведёт к 16 вызовам 4-битного умножения [^14]. А приведение по модулю еще более затратное действие. Тоже не вариант. Алгоритм Карацубы не сильно эффективен для небольших чисел: у нас всё же всего 4 разряда.
Остаётся только всё глубже погружаться в кроличью нору с изначальной бинарной версией умножения, переходя к самым низкоуровневым хакам на уровне ассемблера.
const modularMultiply = (a, b, m) => {
let multipliedFactor = a;
let result = 0;
for (let shiftedFactor = b; shiftedFactor > 0; shiftedFactor = shiftedFactor >> 1) {
if (shiftedFactor & 0x1 === 0x1) {
result = (result + multipliedFactor) % m;
}
multipliedFactor = (multipliedFactor + multipliedFactor) % m;
}
return result;
};Идея заключается в том, что временный результат не обязан принадлежать системе наименьших вычетов, ведь только перед возвратом из функции нам нужно привести его в финальную форму. А значит мы можем убрать шаг приведения по модулю после каждой операции сложения.
Однако не всё так просто - если совсем исключить этот этап, то у нас произойдёт целочисленное переполнения (мы же работаем с 16-битными числами). Изначально, приведение по модулю кодировалось всего лишь одной операцией вычитания:
x = x > m ? x - m : x ибо оба слагаемых всегда были меньше чем . С новым подходом это уже не так и нам нужно подумать как мы будем эффективно приводить числа по модулю.
Переполнение потенциально может произойти только при операциях с числами больше 0x1000. Поэтому нам не обязательно обеспечивать принадлежность чисел к системе наименьших вычетов, а достаточно просто уменьшать их разрядность корректно. Для этого мы заводим небольшую таблицу поиска (LUT) с числами кратными , подобранными так, чтобы вычитанием числа из таблички уменьшить заданную переменную до 3-х разрядов. Само собой, класс вычета этой переменной не меняется (ведь отнимаем число, кратное модулю), так что всё ок. Математически LUT описывается тривиально, ключем в таблице является старший разряд числа:
Для небольших модулей не всегда будет гарантировано то, что после уменьшения с использованием значения из LUT, число будет меньше 0x1000. В таких случаях мы производим еще одно вычитание с использованием другого предвычесленного значения:
Ранее я уже упоминал про числа в форме Монтгомери и то, что мы можем проводить вычисления в этой форме, а выйти из неё только перед вычислением . Мы можем пуступить аналогично - вернуть наши переменные к системе наименьших вычетов прямо перед выполнением деления, а все промежуточные вычисления вести с приближенными значениями.
То, что у нас не всегда точные значения переменных, несколько сказывается на производительности - время выполнения некоторых операций зависит от того, насколько большие числа выступают в качестве операндов. Но если смотреть на картину в целом, то выйгрыш от отказа от точного приведения по модулю куда больше.
Может это прозвучит странно, но на i40xx сложение многоразрядных чисел требует меньше инструкций по сравнению с вычитанием, из-за особенностей флага переноса (или заимствования). Когда мы вычитаем одно число из другого, то флаг заимствования будет установлен в 1 если заимствования не было (уменьшаемое больше или равно вычитаемуму). Но сама операция вычитания интерпретирует этот флаг стандартно, если он установлен, то из уменьшаемого вычитается дополнительная 1. Таким образом, при работе с многоразрядными числами необходимо инвертировать флаг заимствования перед тем как вычитать следующий разряд:
# compute [rr0, rr1] = [rr0, rr1] - [rr2, rr3]
LD rr0
SUB rr2 # acc = rr0 - rr2, borrow flag is 0, if there was borrow
CMC # inverse borrow flag
XCH rr0
LD rr1
SUB rr3 # acc = rr1 - rr3 - borrow, borrow flag is 0, if there was borrow
CMC # inverse borrow flag
XCH rr3В свою очередь, сложение не имеет такой особенности:
# compute [rr0, rr1] = [rr0, rr1] + [rr2, rr3]
LD rr0
ADD rr2 # acc = rr0 + rr2, carry flag is 1, if there was carry
XCH rr0
LD rr1
ADD rr3 # acc = rr1 + rr3 + carry, carry flag is 1, if there was carry
XCH rr3При работе с 16-битными числами мы можем заменить вычитание сложением с
(дополнительный код для
) и получить правильный результат, но с меньшим числом инструкций.
Данная оптимизация является общей, а не специфичной для модульного умножения, но операция вычитания выполняется очень много раз именно в данной функции.
Почти сразу мне бросилось в глаза то, что цикл в функции умножения проходит не больше 16 итераций, и мы можем просто-напросто развернуть его тело:
# assume that rr6 has b[0]
LDM 0x1
AN6
JCN z, mulMod_skipMultiplierBit0 # if ((b >> 0) & 0x1)
JMS mulMod_updateResult # res = res + multipliedFactor
mulMod_skipMultiplierBit0:
JMS mulMod_updateMultipliedFactor # multipliedFactor = multipliedFactor * 2
LDM 0x2
AN6
JCN z, mulMod_skipMultiplierBit1 # if ((b >> 1) & 0x1)
JMS mulMod_updateResult # res = res + multipliedFactor
mulMod_skipMultiplierBit1:
JMS mulMod_updateMultipliedFactor # multipliedFactor = multipliedFactor * 2
# ... 14 more checks for particular bitsНо если подумать получше, то весь алгоритм заключается в череде сложений - на каждой итерации обновляем multipliedFactor и, в зависимости от текущего бита множителя, увеличиваем result. При этом для каждого 4-битного разряда множителя мы знаем конкретную последовательность операций сложения. Например, если текущий разряд множителя равен 0x5 (0b0101), то нам нужно обновить переменную с промежуточным результатом, дважды удвоить multipliedFactor, снова обновить result и опять учетверить multipliedFactor. В коде это выглядит как-то так:
__location(0x2:0x50)
mulMod_processNibble_5: # 0b0101
JMS mulMod_updateResult
JMS mulMod_updateMultipliedFactor
JMS mulMod_updateMultipliedFactor
JMS mulMod_updateResult
JMS mulMod_updateMultipliedFactor
JUN mulMod_updateMultipliedFactorОпираясь на значение регистра, который содержит значение текущего разряда множителя, мы можем совершить прыжок на нужный фрагмент:
# rr12 contains current digit for multiplier, rr13 = 0
JIN r6Нам не важно значение multipliedFactor перед выходом из функции умножения, поэтому для старшего разряда нет необходимости обновлять эту переменную после того, как нам встретился последний единичный бит. Чтоб избавиться от лишних вызовов, заводим еще одну таблицу переходов, сгугубо для обработки последнего разряда:
__location(0x3:0x50)
mulMod_processLastNibble_5: # 0b0101
JMS mulMod_updateResult
JMS mulMod_updateMultipliedFactor
JMS mulMod_updateMultipliedFactor
JUN mulMod_updateResultLastИногда (если не возникает переполнение) мы можем вычислять 16 * multipliedFactor и 8 * multipliedFactor более оптимально, с использованием сдвиговых операций.
Если есть риск переполнения, то просто организуем запасной вариант с несколькими вызовами mulMod_updateMultipliedFactor .
Почти всегда за обновлением значения промежуточного результата следует и обновление multipliedFactor :
JMS mulMod_updateResult
JMS mulMod_updateMultipliedFactorИ здесь мы можем внедрить микро-оптимизацию, создав функцию mulMod_updateResultAndFactor, которая объединит код из mulMod_updateResultи mulMod_updateMultipliedFactor. Каким же образом это нам поможет? Арифметика простая - раньше у нас было 2 инструкции вызова функции и 2 инструкции возврата, а теперь у нас будет 1 инструкция вызова и 1 инструкция возврата. Каждый раз экономим по 3 машинных цикла. Возможно это звучит не очень впечатляюще, но напомню, что модульное умножение ответственно за 60% времени исполнения программы, а так как сама по себе функция выполняется не так долго, то даже такие единичные сохраненные такты позволяют выйграть минуты и десятки минут в общем табеле.
У нас есть контроль за возможным переполнением при удваивании multipliedFactor. Заключается он в проверке на то, что старший разряд этой переменной меньше 0x8. Если это так, то при умножении на 2 мы точно не превысим разрядность:
XCH rr2 # multipliedFactor = multipliedFactor + multipliedFactor
AN7 # check if previous value of multipliedFactor[3] < 4, then new multipliedFactor[3] < 8
JCN z, mulMod_updateResultAndFactor_return # if (multipliedFactor[3] < 0x8)
Проверка знаимает всего 3 машинных цикла, но, как я писал выше, каждый такт на счету. Поэтому я использовал очередной трюк - заменил AN7/JCN одной инструкцией JIN. Да, будет использована еще одна страница ПЗУ под таблицу перехода, но оно того стоило, тем более небольшой запас ROM у нас был. Если в rr2 у нас содержится старший разряд числа, то используя JIN r1 мы обеспечиваем переход на одну их двух ветвей - когда rr0 < 0x8 и когда rr0 >= 0x8. Да, у нас будут две серии по 8 одинаковых блоков кода, но это уже финальные штрихи, и я смогу пережить такое попрание принципов написания чистого кода.
XCH rr2
JIN r1
__location(0x4:0x00)
mulMod_updateMultipliedFactor_factor0:
BBL 0
__location(0x4:0x10)
mulMod_updateMultipliedFactor_factor1:
BBL 0
...
__location(0x4:0x80)
mulMod_updateMultipliedFactor_factor8:
SRC r1
RD0
ADD rr0
XCH rr0
RD1
ADD rr1
XCH rr1
RD2
ADD rr4
XCH rr4
RD3
ADD rr2
XCH rr2
CLC
BBL 0
...Было еще несколько рабочих идей, но, по той или иной причине, они не представлены в финальной версии кода:
Ветвь кода для умножения по 12-битному модулю. Это было эффективно, когда произведение всегда было гарантировано меньше модуля. Тогда для небольших модулей мы могли избавиться от кода работы со старшими разрядами.
Быстрое сравнение переменной со значением модуля. Опять же, до внедрения ленивого приведения мы проводили сравнение довольно часто, дабы сразу когда число становится больше мы могли его уменьшить и вернуть в систему наименьших вычетов. Сама операция сравнения относительно затратная - чтоб сравнить два числа, необходимо вычесть одно из другого и проверить флаг заимствования. Ради ускорения я добавлял еще одну таблицу поиска, ключем являлся старший разряд числа, а значением - индикатор того, точно ли переменная больше модуля.
SRC rX # first register in register pair contains the address of LUT, second register - multipliedFactor[3]
RDM # read isLessThanModulus = LUT[multipliedFactor[3]]
JCN z, ret # return if (isLessThanModulus)Другой, испробованный мною подход по уменьшению ненужных операций вычитания, заключался в том, чтобы держать промежуточный результат меньше 0. После операции сложения, если число становилось положительным (а проверить это нетрудно), то мы вычитали . До этой оптимизации, псевдокод ассемблерной реализации выглядел примерно так:
result = result + multipliedFactor
[tmp, borrow] = result - m
// check if result - m > 0
if (!borrow) {
result = tmp
}После оптимизации:
[result, carry] = result + multipliedFactor
// check if result > 0 now
if (carry) {
result = result - m
}Заметно отличие в количестве операций. Надо только не забыть скорректировать возравщаемое значение, добавив перед выходом из функции.
Объем работы функции модульного умножения напрямую зависит от позиции старшего единичного бита числа, выступающего в качестве второго операнда функции. Следовательно мы должны стараться сделать так, чтобы второй операнд был меньше чем первый. Мы можем их сравнить и поменять местами, если данное условие не выполняется. Результаты были неоднозначными - сама операция сравнения занимает какое-то время и нужно было очень тонко подбирать в каких случаях мы хотим использовать данный функционал, а в каких сравнение будет лишь тратой времени. В итоге, оптимизация стала напоминать подгонку кода под конкретные входные данные и я убрал её.
Можно было завести еще одну таблицу поиска для более точного приведения переменных по модулю. Даже для "ленивой" версии. Но в ОЗУ оставалось не так много свободного места, да и, навскидку, заметный выигрыш был только для небольших модулей, в остальных случаях код мог работать даже медленее.
В предыдущих разделах я упоминал различные таблички, кэши и переменные, которые хранятся в памяти. Сейчас же я решил показать это в более наглядном виде:
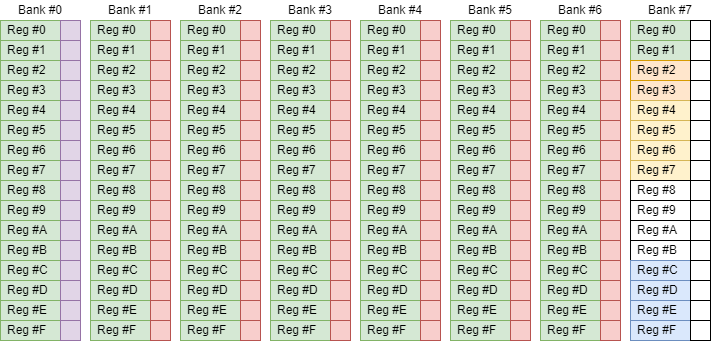
Легенда:
Зелёная секция содержит значения , всего 114 регистров из 128 доступных.
Фиолетовая - таблицы поиска для функции модульного умножения.
Красная - таблицы умножения. Каждая ячейка таблицы занимает 8 бит, а в статусных символах регистра памяти хранится 16 бит (4 слова). Так что каждый банк памяти хранит таблицы для двух множителей. Всего у нас 12 множителей (исключаем 0, 1, 2 и 8), а значит у нас заняты статусные символы в 6 банках.
Оранжевая (очень похожа на жёлтую) - таблица со степенями . Может содержать до восьми 16-битных чисел, то есть 32 байта или 2 регистра памяти.
Жёлтая - карта простоты для текущего сегмента простых чисел.
Синяя - начальный сегмент простых чисел.
Белая - свободна для использования под произвольные переменные.
Весьма плотная компоновка, но, к счастью, чуть больше свободы чем в моём прошлом проекте.
После всего этого безобразия с различными хаками и оптимизациями, программа наконец-то уложилась в отведённые рамки - я получил правильную последовательность цифр π за 69 часов, 29 минут и 02 секунды. Отлично, осталось проверить работу на реальном микропроцессоре.

Электрическая принципиальная схема мало чем отличается от схемы платы для i4004. Основные отличия:
Самостоятельно распаял stm32 на плате со всей обвязкой, вместо использования сторонней отладочной платы, совместимой с DIP сокетом.
Питание Intel 4040 процессора берется с USB, тогда как в прошлой версии требовалось внешнее питания на 20 вольт.
Управление системой происходит через USB, а не через UART интерфейс.
В остальном, компонентая база не поменялась - stm32f4 в качестве эмулятора памяти (ROM и RAM), LM339 и CD40109 для конвертации уровней сигналов с 15 вольт для i4040 на 3.3 вольта для stm32, и обратно.
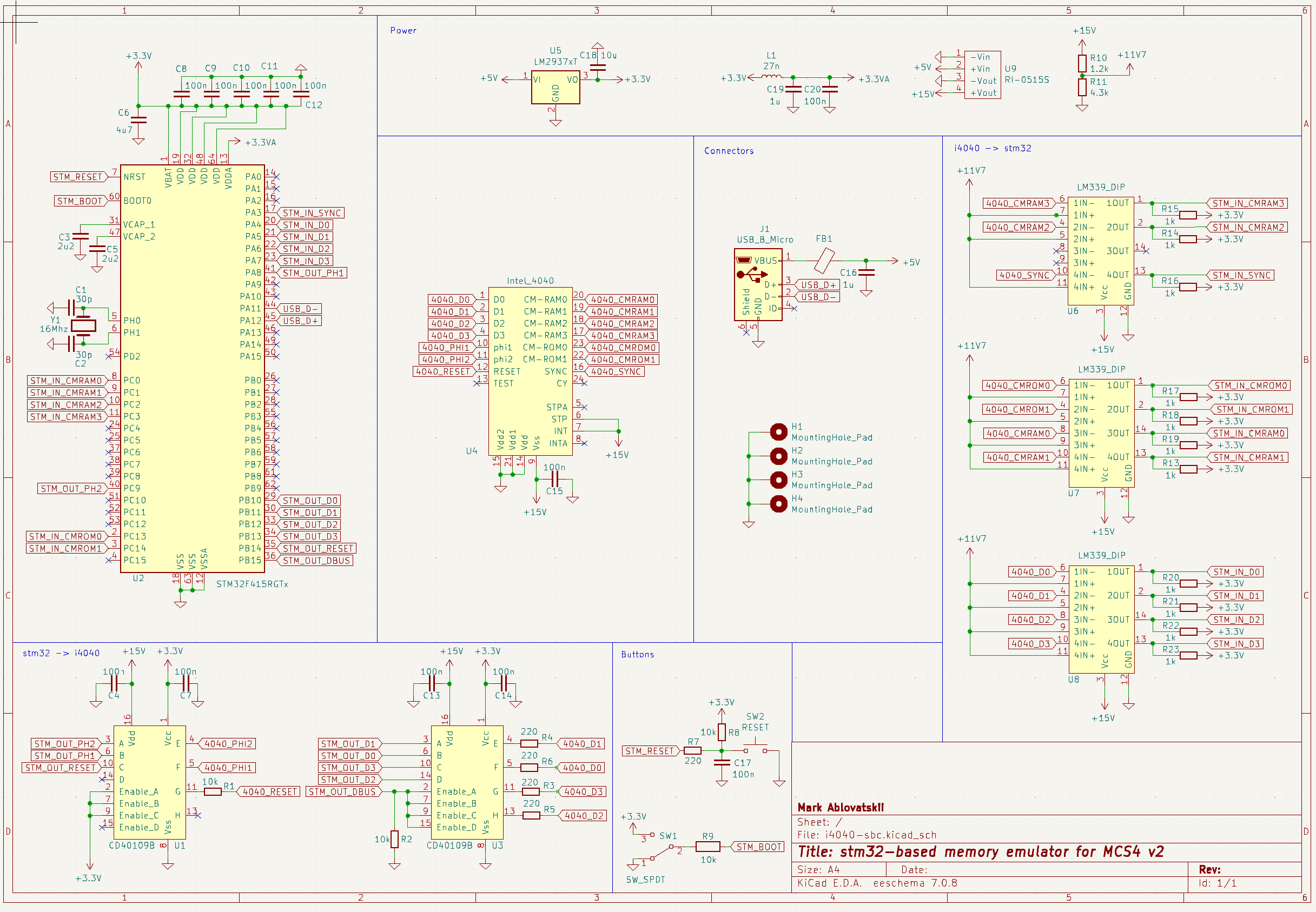
Основу для прошивки я также позаимствовал из оригинального кода для платы с i4004, но пришлось его немного подкорректировать.
Интерфейс памяти у 4040 чуть более продвинутый, чем у 4004: имеется дополнительный пин для выбора банка ПЗУ. Для нас это играет роль, потому что добавляется больше вычислений для определения запрашиваемого адреса. Кроме того, изначально я запускал плату с несколько заниженными значениями тактирующего сигнала, идующего к Intel 4004. 625 килогерц укладывалось в спецификацию процессора, но для того чтобы уложиться в 70 часов, нам нужно брать максимум от процессора, то есть тактировать его частотой в 740 килогерц.
И тогда-то тайминги поплыли - на каждый такт i4040 процессора нужно анализировать входные пины, проводить какие-то вычисления и обновлять сигналы на выходных пинах. При 740 килогерцах, длина такта на i4040 всего 1350нс. При частоте ядра stm32 в 168 мегагерц, у нас всего 200 тактов stm32 на всё про всё.
С оригинальным кодом я перестал укладываться в это узкое окно. Изначально, я использовал перывания от тактирующего таймера, чтобы знать когда начинается такт на i4040, но с таким подходом были неизбежны задержки между фронтом тактового сигнала и стартом моего кода в обработчике прерывания. Я заменил прерывания на примитивный опрос пина:
while ((OUT_4040_PHI1_GPIO_Port->IDR & OUT_4040_PHI1_Pin) == OUT_4040_PHI1_Pin);
OUT_TEST1_GPIO_Port->ODR ^= OUT_TEST1_Pin;
handleCyclePhi1Falling();
OUT_TEST1_GPIO_Port->ODR ^= OUT_TEST1_Pin;Пин TEST1 я использовал для отслеживания сколько времени stm32 тратит на работу между тактами.
Так как тайминги очень жесткие, то я отрубаю все перывания. После того как stm32 получает команду на старт с дампом ПЗУ, всё взимодействие с ПК заморживается. Если Intel 4040 использует инструкцию ввода-вывода для взаимодействия с каким-то внешним устройством через порты эмулированной ROM/RAM, то я просто отслеживаю такую активность и записываю информация в буфер. Как только Intel 4040 переход в состояние HALT (используется инструкция HLT, которой, кстати, не было в i4004), прошивка на stm32 определяет это и отправляет накопленную статистику и вышеупомянутый буфер на ПК.
Само собой, был ряд проблем как в аппаратной, так и в программной частях платы, но в итоге я смог добиться запуска кода на Intel 4040. И тут меня поджидало душераздирающее открытие - я допустил очепятку в коде эмулятора при вычислении времени выполнения программы в секундах. Машинные циклы считались правильно, но для перевода их в секунды я делил на 95000, а должен был на 92500. А это значит, что на тот момент я только думал, что всё почти закончено. Поэтому, скрипя зубами. я вернулся за оптимизацию кода.
Я упомянул этот момент, чтобы показать как важно проводить реальные тесты на настоящем железе, и не довольствоваться оценками, полученными теоретически или даже при симуляции/эмуляции.
В итоге, я добил необходимые несколько процентов скорости выполнения программы, и вернулся к физическому i4040. Не хотелось рисковать и ждать 70 часов без гарантии что код отработает корректно, поэтому сначала я запустил вычисление 255 цифр π, вместо 2048+.
[2023-10-31T12:08:05.527Z] START command has been received, RAM dump size is 8192 bytes
[2023-10-31T13:13:08.988Z] Program has been finished
[2023-10-31T13:13:08.994Z] Instruction cycles processed = 00000000158651E4
[2023-10-31T13:13:08.995Z] Output from i4040 (263 nibbles):
[2023-10-31T13:13:08.995Z] 3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9 5 0 2 8 8 4 1 9 7 1 6 9 3 9 9 3 7 5 1 0 5 8 2 0 9 7 4 9 4 4 5 9 2 3 0 7 8 1 6 4 0 6 2 8 6 2 0 8 9 9 8 6 2 8 0 3 4 8 2 5 3 4 2 1 1 7 0 6 7
[2023-10-31T13:13:08.995Z] 9 8 2 1 4 8 0 8 6 5 1 3 2 8 2 3 0 6 6 4 7 0 9 3 8 4 4 6 0 9 5 5 0 5 8 2 2 3 1 7 2 5 3 5 9 4 0 8 1 2 8 4 8 1 1 1 7 4 5 0 2 8 4 1 0 2 7 0 1 9 3 8 5 2 1 1 0 5 5 5 9 6 4 4 6 2 2 9 4 8 9 5 4 9 3 0 3 8 1 9
[2023-10-31T13:13:08.995Z] 6 4 4 2 8 8 1 0 9 7 5 6 6 5 9 3 3 4 4 6 1 2 8 4 7 5 6 4 8 2 3 3 7 8 6 7 8 3 1 6 5 2 7 1 2 0 1 9 0 9 1 4 5 6 4 8 5 6 6 9 2 3 FКак можете увидеть, это заняло всего час времени, в сравнении с 3.5 часами краникового алгоритма на i4004. Само собой, это не является каким-то объективным сравнением: разные процессоры, разные алгоритмы, даже разные тактовые частоты. Более того, мне кажется, что если я перенесу ряд оптимизаций в краниковый алгоритм, то не факт что он будет медленнее. Тем не менее, было любопытно запустить одну и ту же задачу в разных проектах.
Ободрённый тем, что результат совпал с эмулятором, я отправил программу для вычисления 2048+ цифр и стал ждать примерно 70 часов, когда она завершится. Я даже прилепил два небольших радиатора (снятых с dip-8 микросхем) на сам i4040 процессор ради несколько лучшего охлаждения, хотя, если честно, он грелся не так сильно.

Всё прошло успешно и i4040 смог перебить результат ENIAC'a со временем в 69 часов, 28 минут и 31 секунду.
PS: очень внимательный читатель может заметить, что время исполнения программы на железе отличается от времени на эмуляторе, даже если по тактам совпадение очень близкое. Ответ заключается в том, что выходное тактирование с использованием таймеров stm32 не идеально на 100%, и выходная частота на самом деле около 740.1 килогерца, а эмулятор предполагает то, что процессор запущен на частоте ровно в 740 килогерц. Можно сказать, что я даже немного разонал Intel 4040 (возможно впервые в истории)!
[^1]: Brian J. Shelburne, "The ENIAC's 1949 Determination of π"
[^2]: George W. Reitwiesner, An ENIAC Determination of π and e to more than 2000 Decimal Places
[^3]: Intel Intellec 4/Mod 40 Microcomputer Development System Reference Manual
[^4]: Stanley Rabinowitz and Stan Wagon, "A Spigot Algorithm for the Digits of π"
[^5]: Jeremy Gibbons, "Unbounded Spigot Algorithms for the Digits of Pi "
[^7]: Simon Plouffe, "On the computation of the ݊n'th decimal digit of various transcendental numbers"
[^8]: Fabrice Bellard, "Computation of the n'th digit of pi in any base in O(n^2)"
[^9]: Xavier Gourdon, "Computation of the n-th decimal digit of π with low memory"
[^10]: D. H. Lehmer, "Interesting Series Involving the Central Binomial Coefficient"
[^11]: Intel, "MCS-40 User's Manual For Logic Designers"
[^13]: Hwajeong Seo, Zhe Liu, Yasuyuki Nogami, Jongseok Choi, Howon Kim, "Hybrid Montgomery Reduction"
[^14]: Michael Hutter, Peter Schwabe, "Multiprecision multiplication on AVR revisited"