Структура + предположения > ML? Моделирование продаж байесовскими методами

Привет, я Анатолий Макаревич. Закончил бакалавриат и магистратуру в БГУ (ФПМИ) по направлениям «экономическая кибернетика» и «анализ данных». Уже более трех лет работаю в EPAM на позиции Data Scientist. Мои основные задачи связаны с эконометрикой, анализом временных рядов, байесовским моделированием. Не так давно участвовал в проекте, где мы применяли методы байесовского моделирования в ритейлинговой сети. Тема непростая и интересная. Так как проект под NDA, решил на примере похожего гипотетического проекта показать, как мы решали поставленные перед нами задачи. Обратите внимание, что все материалы и модели доступны на GitHub.
Текст получился длинный. Даю краткое содержание, чтобы вы могли перейти сразу к тому пункту, который вам интересен.
Основы: плавное погружение в Байесовскую тему для тех, кто ранее не был с ней близко знаком. Речь пойдет о структурных вероятностных моделях и алгоритмах оценки параметров байесовских моделей, а также о преимуществах и недостатках байесовского моделирования.
Примеры простых моделей в библиотеке PyMC3.
Практическая часть — гипотетический проект:
· Введение: моделирование продаж.
· Шаг 1: обзор данных и первоначальный анализ.
· Шаг 2: использование стандартного ml.
· Шаг 3: применение байесовские методов (три итерации модели).
· Шаг 4: анализ результатов (и интерпретация).
· Шаг 5: Сравнение ml (lightgbm) и bayesian (pymc3).
Дополнительные материалы, полезные ссылки и ресурсы.
ОСНОВЫ
Вероятностное программирование – это метод моделирования (парадигма), в которой определяются структурные вероятностные модели (обычно графами) и происходит автоматическая оценка параметров этих распределений. Основное свойство моделей в том, что они описывают полное распределение как параметров, так и данных. Кроме того, они генеративные, то есть фокусированы на описание процессов и структур, и байесовские, что позволяет использовать априорные знания при моделировании.
Определяются такие модели в основном с помощью графов, состоящих из распределений (𝛽~𝑁 (𝜇, 𝜎)), преобразований (y=θβ), и даже динамических связей (циклы, рекурсия). Графы же определяются кодом, так же, как и нейросети (Theano, Tensorflow, PyTorch, JAX и другие бэкенды используются для этой цели).
Существуют общие алгоритмы оценки параметров байесовских моделей: метод максимальной апостериорной оценки (maximum a posteriori), метод Монте-Карло с марковскими цепями (MCMC), вариационный вывод (Variational Inference).
Немного углубимся в графовые модели (probabilistic graphical models – PGMs).

Выше вы видите байесовскую сеть, определенную как DAG условных зависимостей между переменными {𝑋1, …, 𝑋𝑛}. Полную функцию распределения можно разложить на перемножение условных распределений. Как раз эта условность и позволяет нам строить вероятностный граф. Получается, наша модель в виде графа эквивалентна этой факторизации. Многие модели, которые используются сейчас на практике, можно использовать в виде таких вероятностных графов.
Примеры «графовых моделей»:
линейная регрессия – 𝑃[𝑦|𝑥] =𝑁 (𝛽𝑥, 𝜎^2)
авторегрессионные модели и цепи Маркова:

модели смесей распределений (mixture models)
нейросети тоже можно представить в таком вероятностном виде
Почему применяется байесовское моделирование? Стандартными методами, к примеру «градиентным спуском», легко решить задачи на математическое ожидание, но необходимо предполагать нормальность для такой оценки. Чаще всего эти строгие предположения не совпадают с реальностью, особенно в более сложных моделях. Кроме того, добавить какие-то собственные предположения в этом случае сложно – придется «хитро» менять функцию потерь. В свою очередь, Байесовский вывод (inference) позволяет оценивать полное распределение вероятности. Для модели с набором данных 𝑋 и параметрами 𝜃, мы можем определить априорное распределение этих параметров, именно здесь и начинается байесовский анализ. Также можно включить другие знания, ограничения, предположения плотности 𝑝(𝜃). Такая модель данных позволяет определить функцию правдоподобия 𝑝(𝑋│𝜃). А при наблюдении этих данных у нас возникает построенная оценка параметров по формуле Байеса: 𝑝(𝜃│𝑋) =(𝑝(𝜃)𝑝(𝑋│𝜃))/𝑝(𝑋) ∝𝑝(𝜃)𝑝(𝑋│𝜃). Это правило можно применить к любым распределениям вероятности, произвольно сложным моделям, используя те же вероятностные графы, которые были описаны ранее.
Размерности таких задач могут быть огромными, поэтому можно получить распределения только путем аппроксимации. Например, распределения можно получить алгоритмами семплирования, которые возвращают эмпирическое распределение в качестве приближения («гистограмма»). Самые популярные алгоритмы для многомерных задач – метод Монте-Карло с марковскими цепями (MCMC), и самый продвинутый и широко используемый из алгоритмов MCMC – NUTS.

Сегодня мы с вами сравним стандартные методы машинного обучения с байесовским моделированием.
Начнем с преимуществ байесовского моделирования:
Оценивается полное распределение модели, а не только среднее значение. Это дает “бесплатные” интервальные оценки, квантили для прогноза и параметров, оценки неуверенности и прочее. Используя этот метод, проще найти проблемные параметры.
Априорные распределения дают нам больше гибкости в описании моделей. Например, если какие-то коэффициенты строго положительные, то можно выдать нулевую вероятность к отрицательным значениям. Байесовское моделирование дает возможность включить бизнес-знания, оценки и результаты предыдущих моделей, добавить жесткие или мягкие ограничения по коэффициентам. Априорные распределения также позволяют работать с малыми (редкими) или шумными данными.
Стоит затронуть основные недостатки:
Обучение намного более вычислительно затратно (Monte Carlo, VI): нелинейная вычислительная сложность приводит к тому, что для больших задач требуется много времени и ОЗУ.
Нишевая область, а следовательно, сложно получить опыт: необходимы глубокие математические знания (распределения, оптимизация). Материалов, которые предоставят информацию для решения сложных задач, в широком доступе мало. Приходится учиться самостоятельно.
Существует проблема сходимости для больших задач.
ПРИМЕРЫ ПРОСТЫХ МОДЕЛЕЙ В БИБЛИОТЕКЕ PYMC3
Начнем с простой модели (univariate normal).
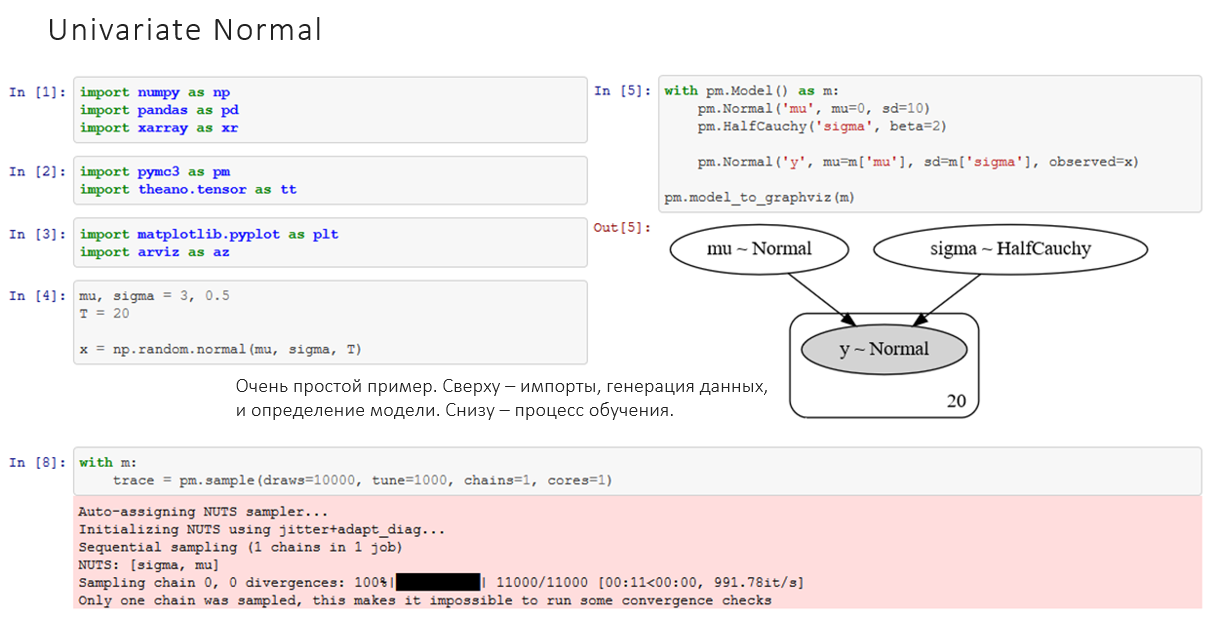
На изображении вы видите код: сверху – импорты, генерация данных, и определение модели. Справа – ее граф. В нижней части иллюстрации – процесс обучения, он здесь очень простой. В PyMC3 есть «магическая» функция «sample», которая вычисляет лучший алгоритм и проводит «семплирование» распределения. Кстати, я сам пользуюсь этой библиотекой и очень рекомендую ее, особенно для начинающих, поскольку она удобна.
А теперь смоделируем двумерное нормальное распределение (multivariate (2D) normal). В этом примере мы брали 40 значений из двухмерного нормального распределения. Следуя советам в документации, мы использовали «LKJ Prior on Cholesky decomposition» для априорной оценки ковариационной матрицы.

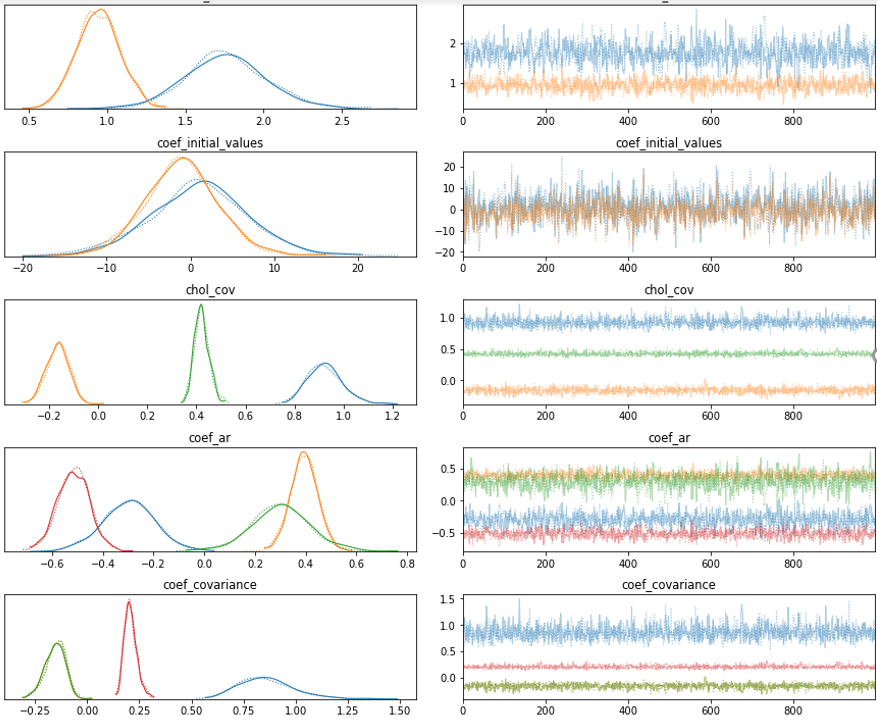
На изображении ниже – вывод обучения такой модели: справа – "трейсы" – значения цепи Маркова, которая аппроксимирует наши распределения, а слева – гистограмма этих оцененных параметров. Для интуиции помогает вообразить, что цепь “схлопнули” горизонтально и получили левую гистограмму. Таким образом, мы получаем оценки распределения вероятности наших параметров.

Перейдем к векторной авторегрессии (VAR). В этом распределении много параметров: константа, начальные значения, авторегрессионная часть и корреляционная матрица. Эта модель определяет функцию распределения для нашего авторегрессионного процесса, то есть всех данных серии. Для имплементации собственного класса (VAR) требуется определить только функцию правдоподобия.

Результаты моделей векторной авторегрессии выглядят следующим образом, снизу - графики цепей и распределения параметров:
А также распределение значений наших процессов в целом: облако из возможных реализаций вектора авторегрессии и область распределения этих значений.
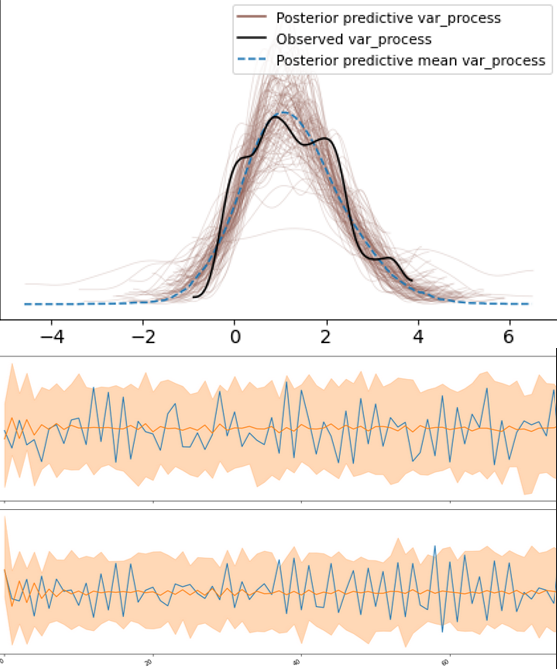
Как вы видите, реализация этой модели, которую мы получили на входе, вероятна. Обратите внимание, что в библиотеке PyMC3 доступны не только нормальные или непрерывные распределения.
Например, в моей магистерской диссертации я использовал модель Пуассоновского распределения с Марковским переключением (переключает параметры по марковской цепи). Рассмотрим ее поподробнее.

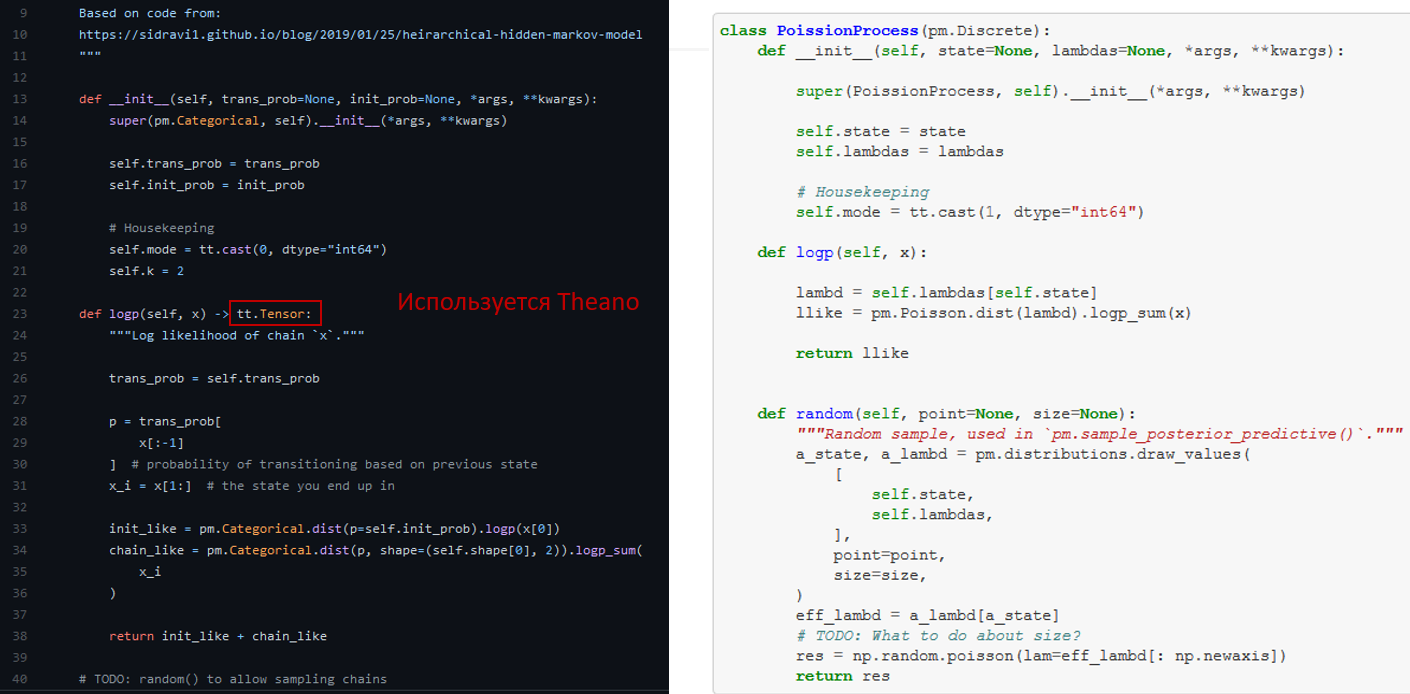
Здесь тоже есть собственные классы, но в целом граф и модель дают ясное понимание того, что происходит. Как видите – есть скрытый марковский процесс (Markov State Transitions), который влияет на пуассоновское распределение. Ниже вы можете видеть наш «страшный» код. В этом случае используется Theano, поскольку PyMC3 построен на нем. Опять же – требуется только функция правдоподобия (logp), но для ускорения можно еще добавить и функцию «семплирование» (random).
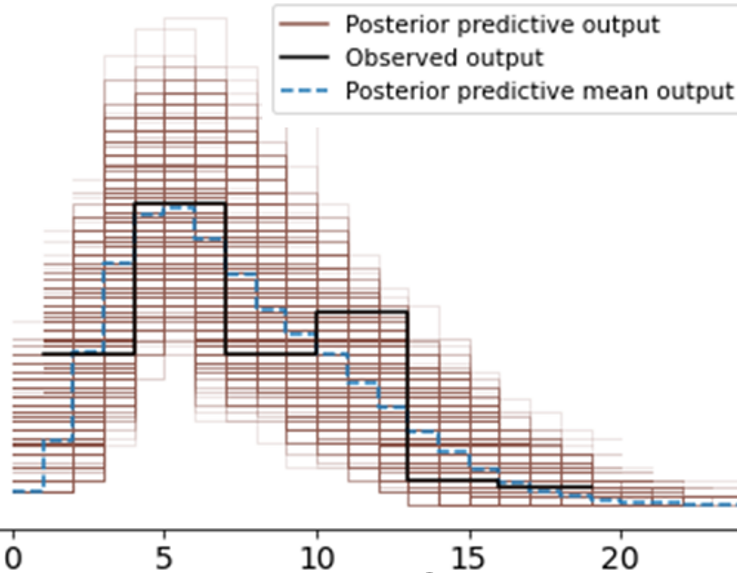
Посмотрим на результат обучения модели Пуассоновского распределение с Марковским переключением на выборке данных. Как видите, мы можем семплировать дискретные распределения. В этом случае NUTS не работает, поскольку дискретные модели не имеют градиентов, но PyMC3 автоматически выбирает правильный алгоритм. На изображении ниже – распределение возможных процессов.
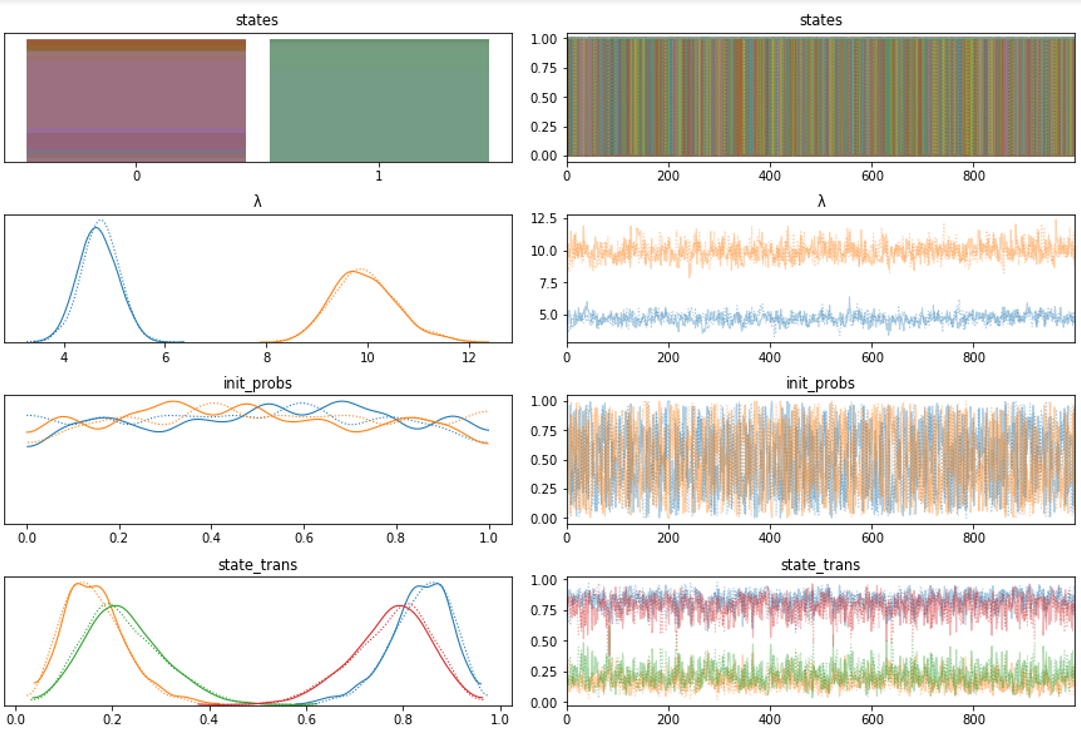
На следующих графиках вы можете увидеть “trace plots” цепей MCMC и распределений для параметров модели.
Ниже – апостериорные предсказания, которые отражают реализацию процесса, включая ненаблюдаемые состояния.
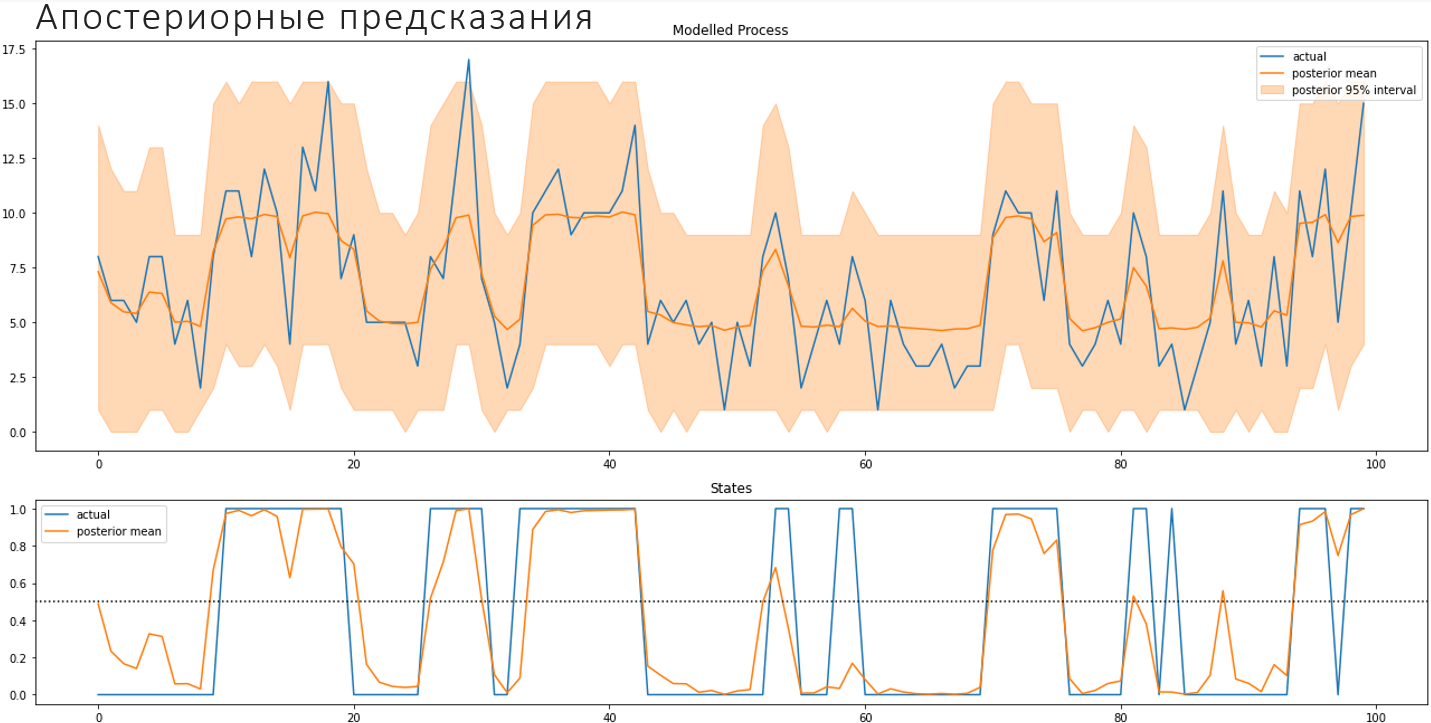
Вывод: Байесовское моделирование позволяет строить структурные статистические модели. Рассчитывать руками, как оценивать параметры, не придется. «Магическая» функция «sample» сделает это за вас. Байесовское моделирование очень гибкое, подходит для моделей любого уровня сложности, при этом дает распределение всех «фичей».
МОДЕЛИРОВАНИЕ ПРОДАЖ: ВВЕДЕНИЕ
Давайте попробуем рассмотреть решение бизнес-задачи, на примере гипотетического проекта. Отмечу, что подобный проект не так давно реализовывали для достаточно крупного заказчика. Возьмем данные, которые предоставлялись компанией Walmart, в рамках соревнования Kaggle – Makridakis M5 Forecasting Competition (03.03.2020-01.07.2020). Участникам необходимо было точно спрогнозировать продажи в некоторых магазинах компании. Предлагаю задачу усложнить и добавить дополнительные требования со стороны заказчика – возможность интерпретации для бизнес-пользователей.
Справка: Makridakis M5 Forecasting Competition – соревнования по моделированию и прогнозированию временных рядов. Walmart – cамая большая ритейлинговая компания в мире (более десяти тысяч магазинов в 24 странах).
Для чего бизнесу необходимо предсказывать продажи? Есть много моментов, которые нужно учитывать, чтобы потребитель мог всегда найти необходимый товар, а бизнес не терял прибыль. Эти факторы напрямую связаны с предположениями об уровнях продаж. Если товара нет на полке – покупатели найдут похожий и возможно более дешевый, либо пойдут в магазин конкурента. Это риск потерянных продаж. Чтобы на полках всегда был необходимый покупателю товар, у магазина есть склад, но место на складе ограничено – хранить большие запасы не получится. Заказать и доставить товар – длительная процедура: логистические цепочки долго доставляют товары от производителя до ритейлера. Грамотное предсказание не только поможет сэкономить место на складе, осуществить заказ партий товара своевременно, но и минимизирует риск потери.
При прогнозировании продаж необходимо учитывать давно известные экономистам факторы, влияющие на потребительский спрос:
Цена (собственная, похожих продуктов, на товары конкурентов)
Реклама в магазине («распродажа», «цена дня» и т. д.)
Внешняя реклама (ТВ, интернет-маркетинг, газеты, борды и баннеры на улице)
Доход населения (в районе магазина, в стране)
Сезоны и праздники
Погода, пандемии, и другие внешние факторы (Помните, что происходило с продажей масок и других средств защиты в начале пандемии?).
Экономисты, менеджеры, специалисты по маркетингу и не только часто используют при прогнозировании важное понятие: эластичность. Эластичность x по отношению к y определяется так:
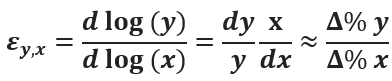
Эластичность – коэффициент относительной чувствительности «игрека» по отношению к «иксу», а именно: на сколько % измениться y, если увеличить x на 1%.
Эластичность спроса по цене (то, на сколько продажи вырастут, если поднять цену на 1%) – в идеальном для магазина случае, равна «-1». Величина отрицательная, поскольку люди покупают меньше товаров, если цена на них растет. Исходя из экономической теории и моего опыта могу сказать, что это значение, чаще всего, колеблется в пределах от «0» до «-1».
Учитывая важность перечисленных факторов, будем строить для нашего гипотетического проекта прогнозную модель, которая может дать ответы на вопросы бизнеса относительно эластичностей. Замечу, нам нужна не только приемлемая точность, но и вменяемые значения, которые бизнес сможет принять.
ШАГ ПЕРВЫЙ: ОБЗОР ДАННЫХ И АНАЛИЗ
Изучим условия. У соревнований M5 Forecasting Competition есть очень удобный Competitor’s Guide, в котором описаны данные. Их также можно посмотреть в отдельном гайде на сайте MOFC.

Все данные организованы иерархично:
3 штата (CA, TX, WI)
10 магазинов
3 категории (Hobbies, Foods, Household)
7 департаментов
3049 разных продуктов
продолжительность около 5 лет (спойлер – использовать будем не все)

Итак, у нас 42840 серий, каждая из которых имеет продолжительность ~5.4 лет, то есть 1913 дней + 28 дней для валидации.
Изучим размерности и переменные. У нас три основные размерности: время (date), иерархия локаций (state, store), иерархия товаров (department, category, item).
Задача – предсказать продажи (sales quantity) на самом низком уровне агрегации (date, item, store).
Нам доступные некоторые вспомогательные факторы:
Ценовые (price): в течение недели
Сезонность: по дню недели, по годам
События (event): “Easter”, “SuperBowl” и т.д.
Кроме того, нужно учесть влияние SNAP (Supplemental Nutrition Assistance Program) – государственная программа оказания денежной помощи хозяйствам с малым доходом в США. В данных имеется информация о том, в какие дни, в каких штатах (магазинах) работает эта программа, поскольку она способствует увеличению покупательской способности.
Вот snapshot данных, предоставленный библиотекой xarray:

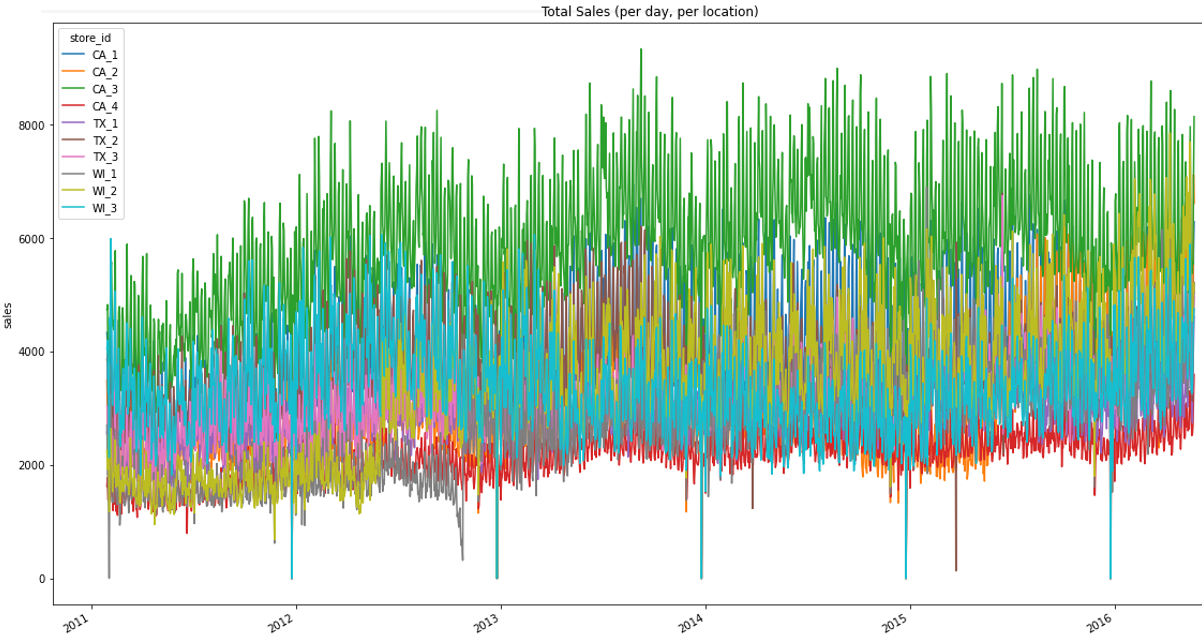
Посмотрим на графики. Вот вид «свысока» – это сумма всех продаж товаров по магазинам. Видна годовая сезонность, недельные колебания, некоторые тренды, сдвиги общих продаж в отдельных торговых точках. Стоит учитывать, что магазины хоть и похожи по размерам, но могут отличаться по площади в 2 и даже в 4 раза.
Если посмотреть на индивидуальную серию (обзор данных «снизу») –- совсем другая картина. Вот выборка шести разных индивидуальных серий.

Данные отличаются от агрегатных. Продажи – проданные единицы, т. е. целые числа. Много малых значений, часто и совсем нулевых. Иногда продукт вообще исчезает, даже если было много продаж ранее – вероятно, произошел «stockout» продукта. Если пытаться предсказывать нормальное распределение, то получится ерунда. Кроме того, стоимость товаров не сильно меняется со временем, значит оценить что-либо по этому параметру будет очень сложно.
ШАГ ВТОРОЙ: ИСПОЛЬЗОВАНИЕ СТАНДАРТНОГО ML
Поскольку большинство из вас знает, какой-то стандартный ML, то начнем с модели LightGBM.
Моменты, которые необходимо учесть:
По условиям конкурса, требуется делать предсказания на много периодов вперед (>28 дней). Мы ограничим себя еще больше, и не будем использовать недавние прошлые значения (лаги) раньше, чем через год.
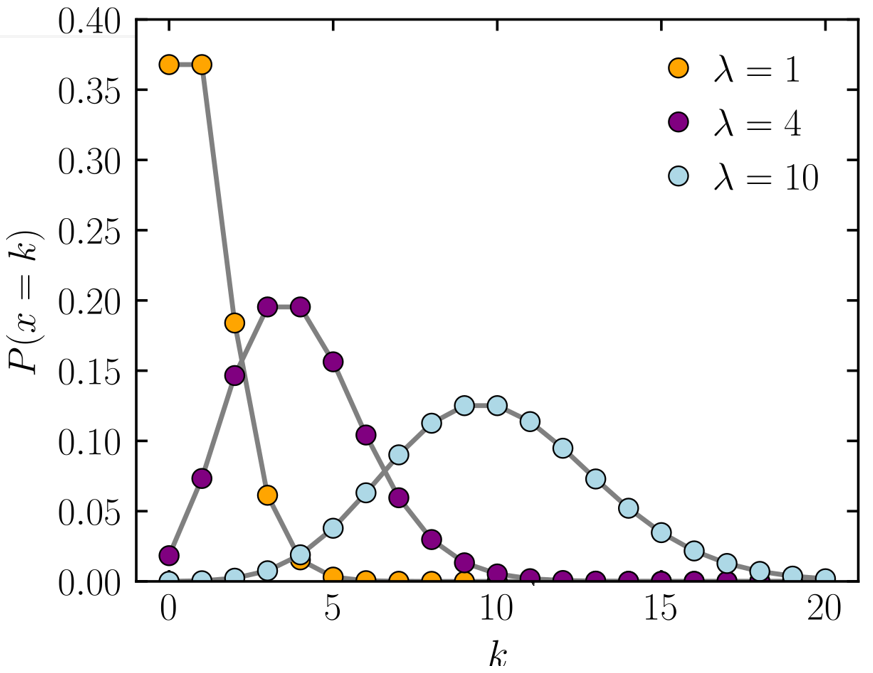
Продажи отдельных продуктов часто имеют малые значения, или и вовсе нулевые, поэтому мы используем Пуассоновскую регрессию: y~Pois(λ),λ=f(x,θ). У LightGBM есть такая objective function.
Критерием точности, по условиям конкурса, является метрика RMSSE, усредненная по всем 12 возможным уровням агрегации. По сути, это сравнение модели со случайным блужданием на один период назад.

По дополнительным бизнес-требованиям нам необходимо оценить эффекты факторов на предсказание. Это значит, что мы не сможем использовать слишком «хитрый» feature engineering для тех переменных, которые хотим оценить. Существуют методы, чтобы обойти это, но сегодня мы не будем углубляться в эту тему.
Из feature engineering мы сможем использовать integer encoding для иерархических координат (category, department, item, state, store; weekday, month). А также, возьмем факторы цены (текущая, и в сравнении с прошлым годом), активности и доступности программы SNAP, средние продажи за аналогичную неделю год назад (365 дней). Стоит включить события (праздники и спортивные мероприятия). Для уменьшения размерности используем следующие фичи: количество событий, номер главного события, номер типа события (религиозное/ национальное/ спортивное/ иное), опережение (лаги по ближайшим событиям). Более сложные трансформации не используем, поскольку важна интерпретация модели и мы ограничены во времени.
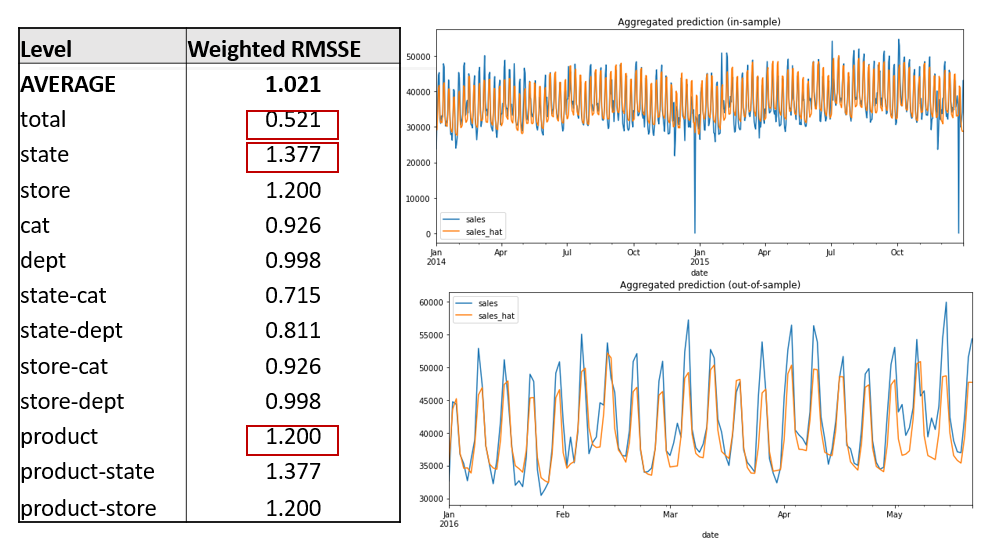
Посмотрим на результаты LightGBM. Напомню, мы специально ставили ограничения на модель. Проведена оптимизация гиперпараметров (200 итераций) и вот лучшие результаты, которые получились. Результаты нашей «ограниченной» модели представлены на разных уровнях агрегации.

Такая модель более или менее одинаково работает на всех уровнях иерархии и чуть лучше «случайного блуждания» (если бы мы могли прогнозировать только на день вперед). Однако, это предсказание большого количества периодов будущего и с ограниченным количеством «фичей», так что результат не так уж и плох. Он стабилен, но мы видим высокий bias, особенно на агрегатном уровне. Возможно, проблему поможет решить дополнительный (но ограниченный) feature engineering. Плюсом будет быстрое обучение: одна модель обучается за 6 минут.
Поскольку нам нужна не только точность, давайте найдем эластичность по цене. Напрямую вычислить коэффициенты эластичности по цене для модели LightGBM не получится, но можно сделать «симуляцию»:
Изменяем цену малыми шагами, т. е. умножаем значения в исходных данных: Δx/x∈[-0.1,0.1].
Делаем предсказания и считаем относительный прирост: Δy/y=f(x+Δx)/(f(x)).
Высчитываем эластичность через формулу, и усредняем по точкам: ε≈xΔy/yΔx≈-0.23.

Оценки эластичности широкие и не уверенные, но в среднем значение примерно около «-0.23». Бизнес, скорее всего, будет скептично смотреть на эти цифры и на огромный «расплыв» по единице.
Давайте посмотрим прогнозы модели на валидационной выборке библиотекой shap: более резонный ответ интерпретации. Если кто-то не знает, shap – это алгоритм и библиотека для аддитивного объяснения эффектов black-box моделей.
Это график эффекта отдельных «фич» на вывод модели.
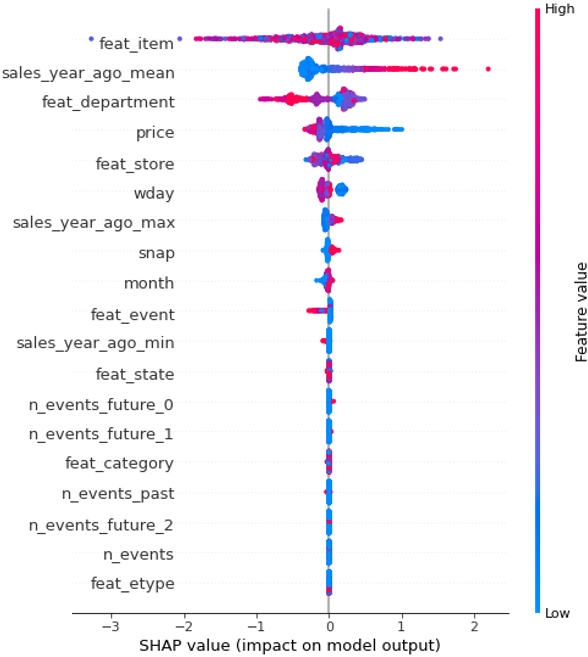
Мы можем оценить их среднюю эластичность, используя лог-регрессию. Вид товара (feat_item), подкатегория и магазин, ожидаемо, ставят средние продажи. Также монотонно участвуют «продажи прошлого года» и есть скопление с нулевыми значениями.
Больше всего нас интересует отклик на цену. Вы легко можете увидеть монотонность на следующем изображении:

SHAP≈Δlog(y) т. к. objective = “poisson”. Оценим Δ log(y)~ ε Δ log(x)+α_0. Получаем ε≈-0.15 – это наша оценка эластичности по SHAP-значениям. Этому значению я доверяю больше, чем нашей «симуляции», но бизнес будет к нему еще более скептичен. Давайте применим Байесовскую регрессию.
ШАГ ТРЕТИЙ: ПРИМЕНЕНИЕ БАЙЕСОВСКИЕ МЕТОДОВ
МОДЕЛЬ I: ПАНЕЛЬ БЕЗ ЛАГОВ
Для начала обучим относительно простую модель на части данных. Создадим панельную модель с регрессией для каждого отдельного товара в каждом магазине, с некоторыми предикторами. Ниже показан граф такой модели.

Берем только часть данных (440 дней, 100 продуктов, 10 магазинов). Использовать будем также только часть факторов: цена, день недели, событие, SNAP. Значительная часть продаж была нулевой, поэтому включаем дополнительный параметр на вероятность нулевой продажи (prob_zero). Игнорируем лаги (в том числе на год назад) и строим регрессию для всех продуктов вместе. В отличие от black-box модели, этот граф показывает некую предполагаемую структуру процесса.
Вот код определения модели, тут не так уж и много.

Предсказание на агрегатном уровне выглядит неплохо, модель предсказывает довольно уверенно, однако сдвиги не подтягивает.

Предсказания на микроуровне (индивидуальные серии) выглядят не так хорошо. Там, где продажи не высокие – мы отлично предсказываем среднее, а для более сложной динамики продаж картина складывается, мягко говоря, «не очень».

Здесь стоит упомянуть одну проблему – объемные модели долго сходятся через чистую Монте-Карло симуляцию (MCMC), поскольку размерность большая. На эту модель потребовалось около 30 часов.

К счастью, есть другие методы оценки параметров. Например, вариационные Байесовские методы (Variational Inference) помогают превращать подобное обучение в нашу любимую задачу «градиентного спуска», то есть в оптимизационную задачу. Auto-Differencing VI (ADVI) – стандартный алгоритм в PyMC3.


Этот способ быстрее, но результат менее точный. В нашем случае результат ADVI дает схожий, но вариативности все-таки больше.
МОДЕЛЬ II: ПАНЕЛЬНАЯ МОДЕЛЬ БЕЗ ИЕРАРХИИ

Попробуем описать более сложную модель. К предыдущей добавим прошлогодние продажи (используем среднее за неделю), изменение цены за период от прошлого года до сегодня, SNAP продажи, и передвинем коэффициент на вероятность нулевых продаж к магазину (c_prob_zero). Не будем включать события из-за их вычислительной сложности. Обучаем на двух годах данных (730 дней), чтобы понять сезонность. Обратите внимание, на графе я выделил дополнительные узлы, благодаря им связи и эффекты теперь более явные.
Агрегатные результаты нашей Байесовской модели меня удивили – они лучше, чем результаты LightGBM, но радоваться рано. В среднем, мы получаем практически сопоставимые предсказания по двум моделям, если смотреть по разным агрегациям. OOS для total мы предсказываем значительно точнее, чем в LightGBM. Однако, для других уровней погрешность выше.
Стоит отметить неприятный момент – обучение на мощной машине заняло 11 часов оптимизации (find MAP – 10 часов и MCMC – 1 час), и потребовало около 60 GB ОЗУ. В сто раз дольше, чем в случае с LightGBM.
МОДЕЛЬ III: ИЕРАРХИЧНАЯ МОДЕЛЬ
Этот вариант еще крупнее двух предыдущих, что заметно даже по графу.

На этот раз снова включаем события (общий коэффициент), а также добавим индикаторы для части нашей иерархии (магазина, департамента), чтобы попытаться уменьшить «расплыв». Кроме того, введем иерархичность для эластичности по цене: “hyper-prior”.

Давайте посмотрим на результаты этой модели. Обучение очень требовательно к ресурсам: около 100 GB ОЗУ (find MAP – около 15 часов и MCMC – 1 час). Из-за ограничений по времени и памяти (параметры доступных мне машин) пришлось приостановить процесс, и это отражается на метриках.
Полученный результат схож с результатом второй модели: примерно такое же соотношение ошибок по уровням. Но, в этом случае, мы правильно предсказываем события на агрегате. Спойлер – наконец получаем адекватные результаты по коэффициентам.
ШАГ ЧЕТВЕРТЫЙ: АНАЛИЗ РЕЗУЛЬТАТОВ
Давайте получим определенные бизнес-результаты для нашего клиента. Начнем с «календарных эффектов»: они не сильно влияют на продажи, кроме Рождества (Christmas), когда магазин закрывается. В остальные дни изменения очень умерены.
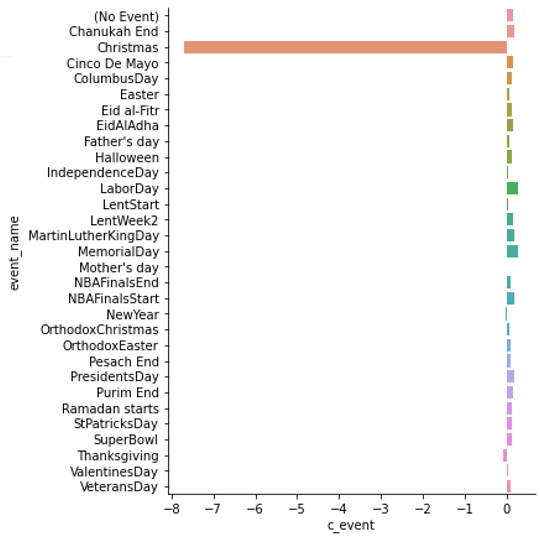
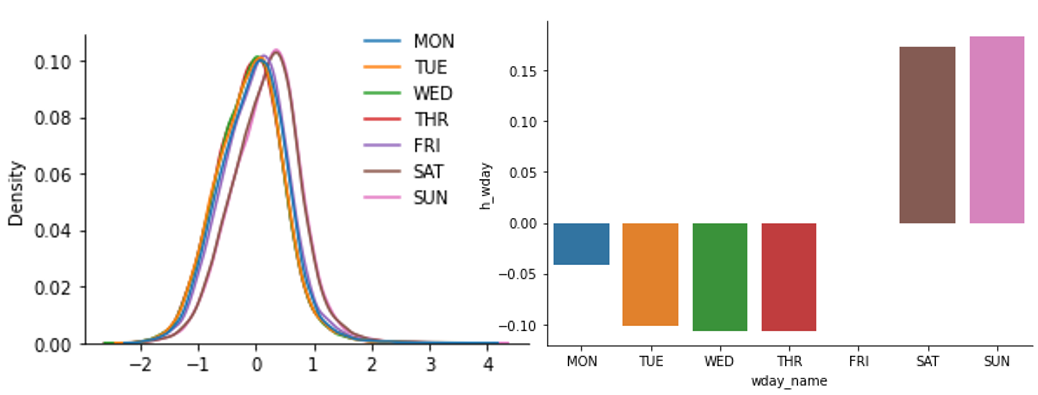
Напоминаю, что это лог-регрессия, поэтому эти коэффициенты имеют экспоненциальный эффект, и их также можно рассматривать как некие эластичности. Если проанализировать дни недели, то мы видим сдвиг на покупки в субботу и воскресенье. Однако, если посмотреть на распределения – это не такой большой сдвиг, как кажется по бар-чарту. Такие выводы очень полезны бизнесу, который ранее рассматривал только точные оценки.
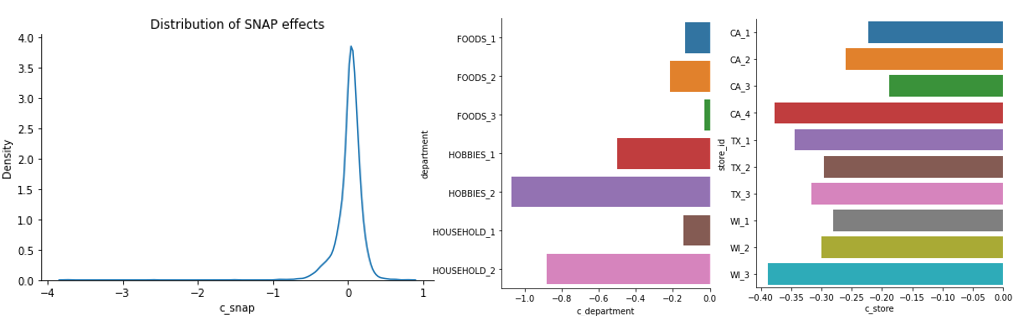
Перейдем к SNAP и категориальным сдвигам. Эффект SNAP близкий к нолю, но это не значит, что фактор совсем бесполезный. Как оказалось, SNAP не сильно влияет на потребительский спрос, но по-разному действует на разные группы товаров, поскольку средства по этой программе можно тратить только на продукты питания. Обратите внимание, что категориальные переменные сдвигали все предсказания вниз, возможно в противовес значениям продаж в прошлом году.
Теперь перейдем к рассмотрению эластичности по цене. Основная цель использования интерпретируемой модели – получение оценок коэффициентов. Наши коэффициенты для цены можно напрямую интерпретировать как эластичности для каждого товара: log(sales)~log(price)+η⇒ ε_price=(d log(sales))/(d log(price))
Если оценить коэффициенты эластичности товаров для простой модели, где мы практически не учитывали различные категории товаров, то мы получим результат похожий на результат black-box модели: ε_price≈-0.216.
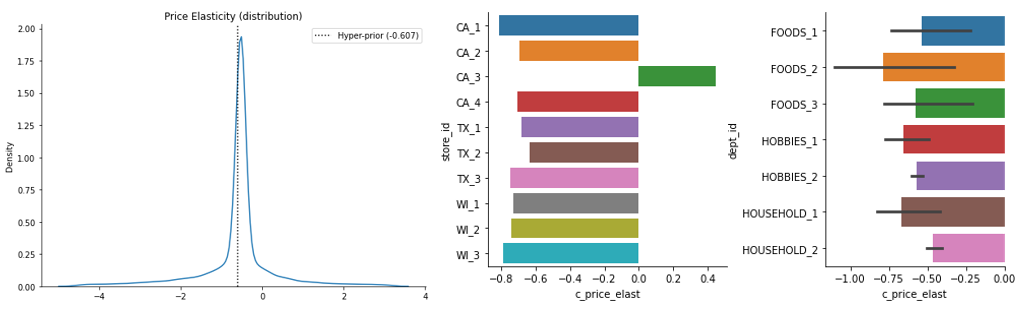
В результатах иерархической модели, где мы использовали категории и дали больше свободы коэффициентам, мы видим более реалистичные значения. Большинство из них, за исключением нескольких «хвостов», имеют отрицательные значения. Среднее значение (ε_price≈-0.607) совпадает с «выученным» hyper-prior, который также равен «-0.6». Это адекватный коэффициент эластичности для анализируемой индустрии. На графиках также видны распределения для средней эластичности по магазину, отделу, городам. Такие выводы важны для разработки ценовой политики различных отделов и категорий товаров.
Вы, наверное, заметили, что у одного из магазинов (CA-3) результаты положительные. Что-то тут пошло не так. Скорее всего, повлияла несвоевременная остановка обучения. Мы можем даже ограничить знаки коэффициентов, чтобы модель не могла давать неправильные знаки, но это стоит делать только после других экспериментов. Этот момент требует более глубокого исследования.
ML (LightGBM) VS. BAYESIAN (PyMC3)
Оба подхода к моделированию имеют свои плюсы. Однако, байесовская модель получилась значительно более понятной и позволила напрямую определить функциональную зависимость, построить интерпретируемую модель, получить значения эластичности. Это дает более точные ответы бизнесу на ключевые вопросов относительно продаж. Тем не менее, она требует очень много времени и памяти при обучении. Опираясь на опыт, скажу, что бизнес вероятнее поверит результатом именно байесовской модели. Однако, использовать можно любую из них. И конечно же, обе модели можно чинить и улучшать.
ML (LightGBM)
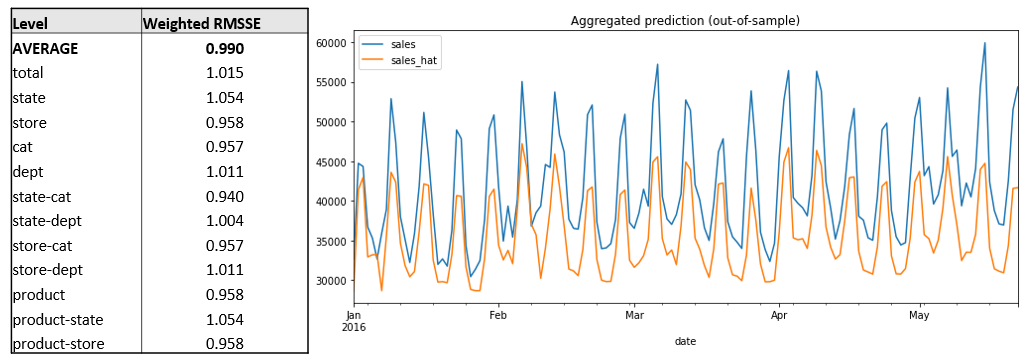
ε_price≈-0.23,-0.15
BAYESIAN (PyMC3)
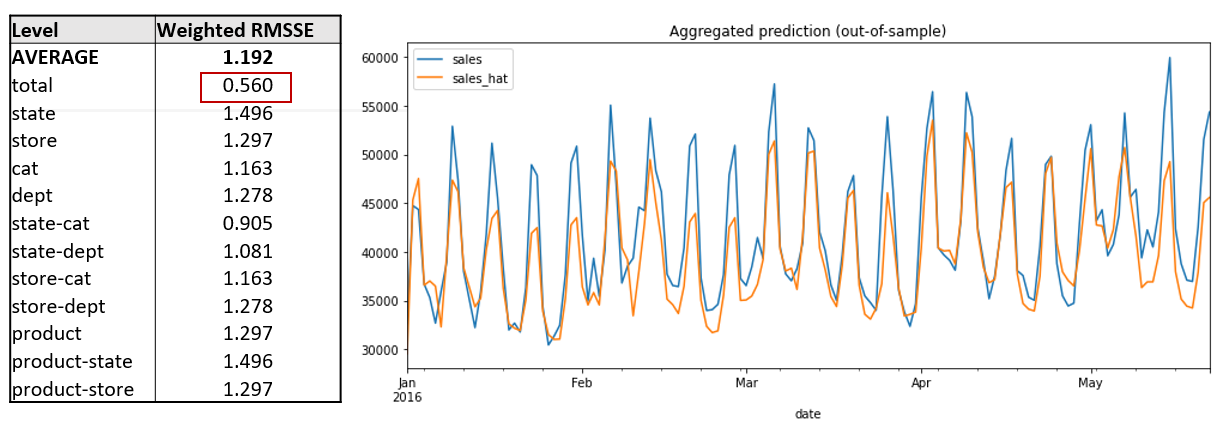
𝜀_𝑝𝑟𝑖𝑐𝑒 ≈ −0.22, −0.61
ВЫВОДЫ:
Байесовские модели отлично подходят для эконометрического моделирования, особенно в ритейле. Их отличает интерпретируемость (ключевое преимущество байесовских моделей), гибкость в построении структуры модели. Кроме того, существует много экономической теории, которая может подсказать, как следует структурировать модель, какие priors брать, какие задачи можно помочь заказчику решить. Однако, такие модели далеко не везде применимы. Если не важна интерпретация, скорее всего стоит использовать более дешевые варианты.
Байесовское моделирование дает возможность делать вероятностные предсказания (распределение, а не только точка), включая неуверенность. Априорные распределения позволяют задавать твердые или мягкие ограничения, использовать иерархическую группировку, быть робастным при малом количестве наблюдений (например, в редких группах). Наконец, это меняет ваш взгляд на задачу и на подходы к ее решению.
Однако, стоит помнить и о главных минусах:
Понадобится значительно больше вычислительной мощности (времени, памяти), т. к. оценивает полное распределение.
Нетривиальные задачи требуют более глубокого понимания теории вероятности, распределений, оптимизации, интуиции алгоритмов MCMC/ADVI.
Бывают частые проблемы со сходимостью, надо наловчиться.
Наконец, предложу некоторые способы ускорить Байесовские методы. Процесс обучения пройдет быстро (около часа) для задач, у которых мало наблюдений или данных (ориентировочно – ниже 20 переменных и 2000 наблюдений). Для более крупных моделей я рекомендую разбивать моделирование на отдельные компоненты, или применять другие «трюки». Например, в этой презентации использовались оценки MAP + MCMC, с целью ускорения сходимости.
ПОЛЕЗНЫЕ ССЫЛКИ И РЕСУРСЫ
Мне еще о многом хотелось бы вам рассказать, но текст и так вышел очень длинным. За кадром осталось много теории, более сложный код, другие байесовские библиотеки (Stan, Pyro, TFP, Turing.jl), Байесовские нейросети. Поэтому подскажу, где искать информацию самостоятельно:
Stan User’s Guide – введение в Байесовское моделирование через язык Stan, со ссылками на продвинутый материал. Stan – золотой стандарт в этой области, но PyMC3, на мой вкус, удобнее
Другие библиотеки: Turing.jl, Pyro, NumPyro, Tensorflow Probability
Кроме этого, я очень рекомендую прочесть книгу Bishop, C.M. – Pattern Recognition and Machine Learning (2006), глава 8 и далее.
Если вам интересно посмотреть на мои примеры имплементации других моделей в PyMC3 (для магистерской диссертации) – вот ссылка.
