https://habrahabr.ru/post/325502/

• Python

Цель работы

В моей статье [1] рассмотрен метод гармонической линеаризации для исследования систем управления, содержащих нелинейные элементы.

Этот метод может быть использован в том случае, когда линейная часть системы является низкочастотным фильтром, т.е. отфильтровывает все возникающие на выходе нелинейного элемента гармонические составляющие, кроме первой гармоники [2]. Поэтому логическим продолжением моей первой статьи будет гармонический анализ рассмотренных нелинейных элементов. Кроме этого нужно рассмотреть аппаратную альтернативу методу гармонической линеаризации.

Метод анализа и программный код

Пусть на нелинейные элементы поступает чистый синусоидальный сигнал. Методом разложения в дискретный ряд Фурье получим его спектр.

#!/usr/bin/env python
#coding=utf8
from numpy import array, arange, abs as np_abs
from numpy.fft import rfft, rfftfreq
from math import sin, pi
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
FD = 250000#частота дискретизации, отсчётов в секунду
N = 2500#длина входного массива, N/FD секунд 
F=250.0#циклическая частота входного сигнала
w=(2.*pi*F/FD)#отсчёт круговой частоты 
A=3.0#амплитуда сигнала
B=0.5#порог ограничения
#сгенерируем чистый синусоидальный сигнал с частотой F длиной N
sin_sig = array([A*sin(w*t) for t in range(N)])#график сигнала
plt.plot(arange(N)/float(FD), sin_sig, 'r')
plt.xlabel('Время, сек.')
plt.ylabel('Амплитуда  сигнала')
plt.title('Входной синусоидальный сигнала')
plt.grid(True)
plt.show()
spectr_sin = rfft(sin_sig )#вычисляем дискретное действительное rfft  преобразование Фурье
plt.plot(rfftfreq(N, 1./FD), np_abs(spectr_sin)/N) #график спектра
plt.xlabel('Частота, Гц')
plt.ylabel('Амплитуда  сигнала')
plt.title('Спектр синусоидального сигнала')
plt.grid(True)
plt.show()

Получим сигнал и спектр сигнала с выхода нелинейного элемента с «насыщением».

# сгенерируем сигнал нелинейности c «насыщением» из A*sin(w*t) при abs(А)>abs(B)
sinp_sig =array([A*sin(w*t) if abs(A*sin(w*t))<B else A*sin(w*t)*B/abs(A*sin(w*t)) for t in range(N)])
plt.plot(arange(N)/float(FD), sinp_sig, 'r')#график сигнала
plt.xlabel('Время, сек.')
plt.ylabel('Амплитуда  сигнала')
plt.title('Форма сигнала c  насыщением')
plt.grid(True)
plt.show()
spectr_sinp = rfft(sinp_sig )
plt.plot(rfftfreq(N, 1./FD), np_abs(spectr_sinp)/N)#график спектра
plt.xlabel('Частота, Гц')
plt.ylabel('Амплитуда сигнала')
plt.title('Спектр сигнала с насыщением')
plt.grid(True)
plt.show()

Для учёта знака ограничения B использован следующий код — A*sin(w*t)*B/abs(A*sin(w*t).

Получим вид сигнала и спектр нелинейного элемента с переходом амплитуды в ноль.

# сгенерируем сигнал нелинейности «cо спадом до нуля»  из A*sin(w*t) при abs(А)=abs(B)
sinn_sig = array([A*sin(w*t) if abs(A*sin(w*t))<B else 0 for t in range(N)])
plt.plot(arange(N)/float(FD), sinn_sig, 'r')
plt.xlabel('Время, сек.')
plt.ylabel('Амплитуда  сигнала')
plt.title('Форма сигнала cо спадом')
plt.grid(True)
plt.show()
spectr_sinn = rfft(sinn_sig )
plt.plot(rfftfreq(N, 1./FD), np_abs(spectr_sinn)/N)#график спектра
plt.xlabel('Частота, Гц')
plt.ylabel('Амплитуда сигнала со спадом ')
plt.title('Спектр сигнала со спадом')
plt.grid(True)
plt.show()

Результаты

Сигнала на входе и на выходе нелинейных элементов.







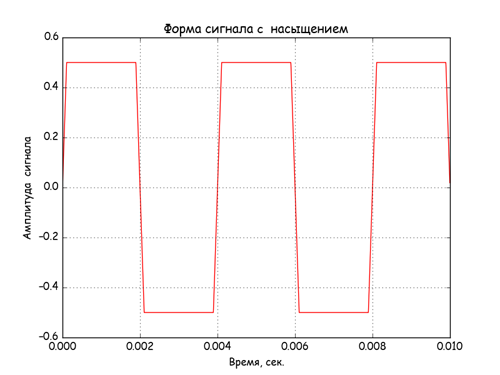
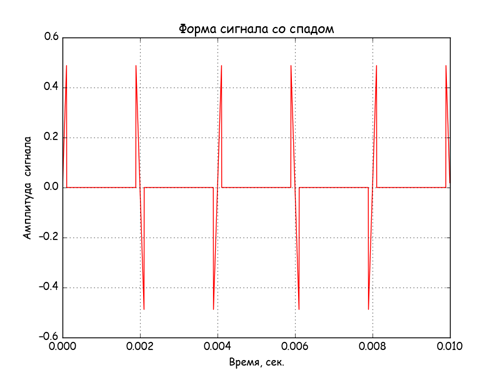
Спектры сигналов на выходе нелинейных элементов.





Нелинейный элемент со спадом сигнала генерирует большое число высокочастотных гармоник. Для фильтрации сигнала на выходе нелинейных элементов можно применить цифровой НЧ фильтр, детально описанный в работе [3]. Для исследования возможностей цифровой фильтрации сигналов нелинейных элементов в код программы [3], были внесены следующие изменения.

A=1.0
B=0.4
test_n = 2560 # Кол-во отсчётов тестового сигнала
test_f = 200 # Наименьшая отличная от нуля частота тестового сигнала
test_period_count = 10.0 # Кол-во периодов тестового сигнала
test_t = numpy.linspace(0.0, test_period_count/test_f, test_n)
# Базовый сигнал sin(wt), подлежащий восстановлению фильтром
test_base_signal = array([A*sin(2*pi*test_f* i) for i in test_t ])
test_signal =array([A*sin(2*pi*test_f* i) if abs(sin(2*pi*test_f* i))<B else 0 for i in test_t ])
#test_signal=array([A*sin(2*pi*test_f* i) if abs(A*sin(2*pi*test_f* i))<B else A*sin(2*pi*test_f* i)*B/abs(A*sin(2*pi*test_f* i)) for i in test_t ])

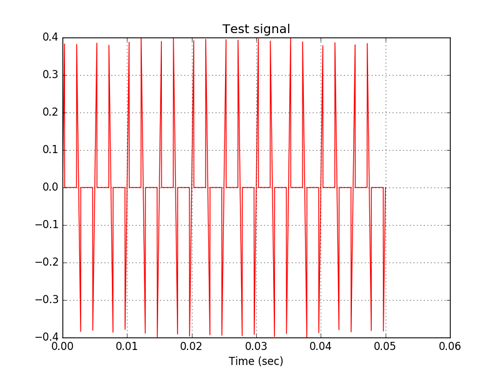
Спектр сигнала на выходе фильтра.

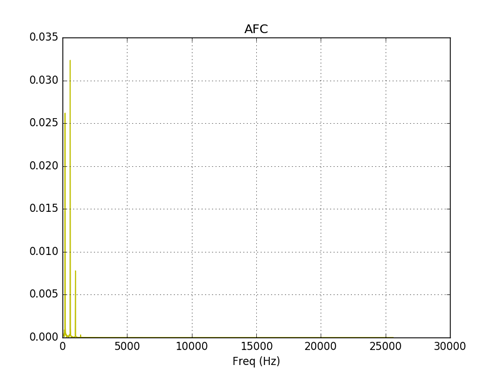
Вывод

Решить задачу использования нелинейных элементов можно аппаратно используя микропроцессор, но при этом необходимо согласование уровней сигналов, а так же ЦАП и АЦП.

Ссылки

1. Метод гармонической линеаризации средствами Python
2. Метод гармонической линеаризации
3. Цифровой фильтр