news.shamcode.ru | Спасёт ли Python от казни?

Спасёт ли Python от казни?

суббота, 8 июля 2017 г. в 03:11:37

Программирование
Математика
Python

Доброго времени суток! При просмотре экшн-фильмов (фильмов с хорошо продуманными динамичными сценами) иногда закрадывается в голову: а реально ли это в действительности? Например, мог ли автомобиль перевернуться на маленькой скорости, как быстро можно раскачаться на верёвке без начальной скорости над пропастью…

Что говорит на это физика? Интересно ли писать на бумажечке и потом хвастаться клочком с формулами и парой-тройкой векторов? Давайте сделаем это безопасно и наглядно.

Начнём с обычного математического маятника:

$\dfrac{m \dot{\theta }^2}{2l^2}+mgl(1-cos \ \theta )=E$

$\ddot{\theta}+\dfrac{g}{l} \ sin \ \theta=0$

$sin \ x\approx x$

Кстати, даже если принимать синус за его аргумент, то эксперименты с измерением периода маятника дают хорошие результаты для g. Но нам, чтобы полюбоваться большими углами, надо честно решить уравнение, особенно если scipy такую возможность предоставляет.

Разделим уравнение на два первого порядка и запишем в стандартном виде

$\dfrac{d}{dt}\begin{pmatrix} \theta \\ \omega \end{pmatrix}=\begin{pmatrix} \omega \\ -g/l \ sin\ \theta \end{pmatrix}$

И теперь смело это кормим нашему змею (подробнее об scipy.integrate.odeint, увы, в оригинале).

t = linspace(0,15,100)
G = 9.8
L = 1.0

def diffeq(state, t):
    th, w = state
    return [w, -G/L*sin(th)]
dt = 0.05
t = np.arange(0.0, 20, dt)

th1 = 179.0
w1 = 0.0
state = np.radians([th1, w1])
y = odeint(diffeq, state, t)

На первом курсе в лаборатории механики были маятники, возможности каждого из них почти исчерпывало задание к работе. А ~~вот с одним было что-то не то, потому что так было нельзя~~ больше всего привлекал внимание маятник Обербека: «Что будет, если не закрепить грузики?»

И вот спустя N лет я увидела в фильме (очередные пираты Карибского моря) что же произойдёт!

Хмммм а действительно ли это так? Для этого достаточно записать всего два уравнения

$a = a_{central} - g \ cos \ \theta, a_{central} = \dot{\theta}^2 r \\ \ddot{\theta} = -\dfrac{g}{r} \ sin \ \theta$

Куда делась масса гильотины? Как и в большинстве задачек без трения она была и справа, и слева от равенства, и ни на что не влияет.

У нас появилась ещё одна переменная r — это расстояние грузика от центра. Запишем окончательно выражение для scipy:

$\begin{cases} \ddot{r} = \dot{\theta}^2r-g \ cos \ \theta, \\ \ddot{\theta} = -g/r \ sin \ \theta \end{cases}$

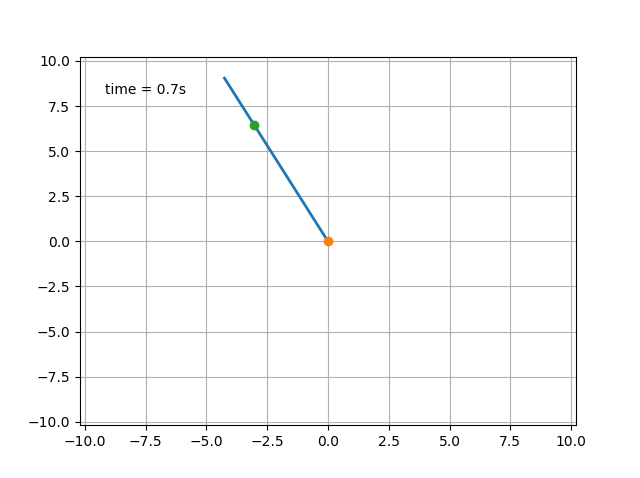
import matplotlib.animation as animation
from pylab import *
from scipy.integrate import *
import matplotlib.pyplot as plt

t = linspace(0,15,100)
G = 9.8
L = 10.0

def derivs(state, t):
    th, w, r, v  = state
    if 0.<r<L:
        return [w, -G/r*sin(th), v, w**2*r-G*cos(th)]
    return [w,0,v,0]

dt = 0.01
t = np.arange(0.0, 20, dt)

th1 = 180.0 #начальные параметры
w1 = 10.
r1 = L
v1 = 0.0

state = np.radians([th1, w1, r1, v1])
y = odeint(derivs, state, t)

x1 = L*sin(y[:, 0])
y1 = -L*cos(y[:, 0])
x2 = (L-y[:,2].clip(min = 0, max = L))*sin(y[:, 0])
y2 = -(L-y[:,2].clip(min = 0, max = L))*cos(y[:, 0])

fig = plt.figure()
ax = fig.add_subplot(111, autoscale_on=False, xlim=(-L-0.2, L+0.2), ylim=(-L-0.2, L+0.2))
ax.grid()

line, = ax.plot([], [], '-', lw=2)
point, = ax.plot(0,0,'o', lw=2)
extra, = ax.plot(x1/L*r1,y1/L*r1,'o', lw=2)
time_template = 'time = %.1fs'
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)


def init():
    line.set_data([], [])
    point.set_data(0,0)
    time_text.set_text('')
    extra.set_data(x1/L*r1,y1/L*r1)
    return line, time_text, point, extra

def animate(i):
    thisx = [0, x1[i]]
    thisy = [0, y1[i]]
    thisx2 = x2[i]
    thisy2 = y2[i]
    point.set_data(thisx[0],thisy[0])
    line.set_data(thisx, thisy)
    time_text.set_text(time_template % (i*dt))
    extra.set_data([thisx2,thisy2])
    
    return line, time_text, point, extra

ani = animation.FuncAnimation(fig, animate, np.arange(1, len(y)),
                              interval=25, blit=True, init_func=init, repeat = False)

plt.show()

P.S. здесь начала копать.
P.S.S. поигравшись с начальными параметрами (для маленьких углов отклонения от вертикали или небольших начальных угловых скоростей) можно прийти к «плоскому» пониманию устойчивости гироскопов.
UPD

А здесь видно, что у бедолаги не только нет шансов, но и вращение ни к чему хорошему не приведёт

Спасти оранжевую точку мне так и не удалось, поэтому будем добрыми и лежать подальше от гильотин, которые из фильмов кажутся безопасными!