https://habr.com/ru/post/466123/

• Python
• Математика
• Машинное обучение

В поиске интересного и простого ДатаСета я набрёл этого красавца.

Об этом красавце

В нём есть данные о росте и весе 10 000 мужчин и женщин. Никакого описания. Ничего «лишнего». Только рост, вес и метка пола. Эта таинственная простота мне понравилась.

Что ж, начнём!

Что мне было интересно?

• В каком диапазоне вес и рост у большинства мужчин и женщин?
• Какие они — «средний» мужчина и «средняя» женщина?
• Сможет ли простенькая модель машинного обучения «KNN» по этим данным угадать вес по росту?

Погнали!

Первый взгляд

Для начала подгрузим нужные модули

# Для работы с табличными данными
import pandas as pd

# Для моих любимых графиков
import matplotlib.pyplot as plt
%matplotlib inline

# Модель машшиного обучения «К ближайших соседей»
from sklearn.neighbors import KNeighborsRegressor
# Для разбивки данных на тренировочный и тестовый наборы 
from sklearn.model_selection import train_test_split

Когда библиотеки встали ровно — пришло время загрузить сам ДатаСет и посмотреть на первые 10 элементов. Это нужно, чтобы наше нутро было спокойно, что мы всё загрузили правильно.

Кстати, не пугайтесь, что рост и вес отличаются от привычных нам. Это из-за другой системы измерений: дюймы и фунты, вместо сантиметров и килограмм.

data = pd.read_csv('weight-height.csv')
data.head(10)

Хорошо! Мы видим, что первые десять записей — «мужчины». Мы видим их рост (height) и вес (weight). Данные подгрузились хорошо.

Теперь можно посмотреть на количество строк в наборе.

data.shape
>> (10000, 3)

Десять тысяч строк / записей. И у каждой по три параметра. То, что нужно!

Пришло время исправить систему измерений. Теперь тут сантиметры и килограммы.

data['Height'] *= 2.54
data['Weight'] /= 2.205

# И проверим результат
data.head(10)

Вот теперь стало привычнее. И первая же запись нам говори о мужчине с ростом ~190см и весом ~110кг. Большой человек. Назовём его Боб.

Но как понять: это много или мало по сравнению с остальными? Возможно ли, что мы все плюс-минус Бобы? Это немного позже.

А сейчас узнаем, насколько симметрично в этом наборе данных сочетаются два гендера?

data['Gender'].value_counts()

>> Male      5000
   Female    5000
   Name: Gender, dtype: int64

Идеально поровну. И это хорошо, ведь если бы было: 9999 мужчин и 1 женщина, то не осталось бы смысла делать вид, что этот ДатаСет одинакого хорошо раскрывает оба пола. В нашем случае — всё ок!

Разделяй и изучай!

Сейчас интуиция подсказывает, что будет правильно разделить два пола и исследовать отдельно. Ведь в жизни мы часто видим, что мужчины и женщины имеют плюс-минус разные рост и вес

# Мужчины
data_male = data[data['Gender'] == 'Male'].copy()

# Женщины
data_female = data[data['Gender'] == 'Female'].copy()

Давайте взглянем на небольшую описательную статистику, которую нам предлагает модуль pandas.

Мужчины:

data_male.describe()

Женщины:

data_female.describe()

Видим, что у мужчин среднее и медиана: 175см и 85кг. А у женщин: 162см и 62кг. Это говорит нам, что сильных выбросов нет. Либо они симметричны в обе стороны от медианы. Что бывает очень редко.

Но у обоих полов есть небольшие отклонения среднего от медианы. Но они несущественны и их видно только на сотых долях. Идём дальше!

Гистограма

Это график, который строит значения от минимума до максимума в порядке роста, и показывает количество отдельных экземпляров.

fig, axes = plt.subplots(2,2, figsize=(20,10))
plt.subplots_adjust(wspace=0, hspace=0)

axes[0,0].hist(data_male['Height'], 
               label='Male Height', 
               bins=100, 
               color='red')

axes[0,1].hist(data_male['Weight'], 
               label='Male Weight', 
               bins=100, 
               color='red', 
               alpha=0.4)

axes[1,0].hist(data_female['Height'], 
               label='Female Height', 
               bins=100, 
               color='blue')

axes[1,1].hist(data_female['Weight'], 
               label='Female Weight', 
               bins=100, 
               color='blue', 
               alpha=0.4)

axes[0,0].legend(loc=2, 
                 fontsize=20)

axes[0,1].legend(loc=2, 
                 fontsize=20)

axes[1,0].legend(loc=2, 
                 fontsize=20)

axes[1,1].legend(loc=2, 
                 fontsize=20)

plt.savefig('plt_histogram.png')
plt.show()

Данные распределяются колоколообразно. Очень похоже на нормальное распределение.

Помимо статистических тестов на нормальность распределения есть визуальный тест. Если распределение по виду и логике похоже на нормальное — можно считать с долей допущений, что мы имеем дело именно с ним.

Можно было бы сделать статистический тест на нормальность и определить p-value, но не умею это выходит за рамки статьи.

Учимся работать ручками

Pandas за нас может посчитать многое. Но нужно хотя бы раз посчитать некоторые статистики самому. Сейчас покажу, как скалькулировать стандартное отклонение.

Сделаем это на примере мужчин и характеристике — рост.

Среднее

Формула:

$$

, где

• М — среднее значение
• N — количество экземпляров
• ni — отдельный экземпляр

Код:

mean = data_male['Height'].mean()
print('mean:\t{:.2f}'.format(mean))

>> mean:    175.33

Средний рост — 175см

Квадрат отклонения от среднего

$$

, где

• di — отдельное отклонение
• ni — отдельный экземпляр
• M — среднее

Код:

data_male['Height_d'] = (data_male['Height'] - mean) ** 2
data_male['Height_d'].head(10)

>> 0    149.927893
   1      0.385495
   2    166.739089
   3     47.193692
   4      4.721246
   5     20.288347
   6      0.375539
   7      2.964214
   8     25.997623
   9    200.149603
   Name: Height_d, dtype: float64

Дисперсия

Формула:

$$

, где

• D — значение дисперсии
• di — отдельное отклонение
• N — количество экземпляров

Код:

disp = data_male['Height_d'].mean()
print('disp:\t{:.2f}'.format(disp))

>> disp:    52.89

Дисперсия — 53

Стандартное отклонение

Формула:

$$

, где

• std — значение стандартного отклонения
• D — значение дисперсии

Код:

std = disp ** 0.5
print('std:\t{:.2f}'.format(std))

>> std: 7.27

Стандартное отклонение — 7

Доверительные интервалы

Сейчас мы узнаем, в каких диапазонах роста и веса находятся 68%, 95% и 99.7% мужчин и женщин.

Это не так сложно — нужно прибавлять и отнимать стандартное отклонение от среднего. Выглядит это так:

• 68% — плюс-минус одно стандартное отклонение
• 95% — плюс-минус два стандартных отклонения
• 99.7% — плюс-минус три стандартных отклонения

Напишем вспомогательную функцию, которая будет считать это:

def get_stats(series, title='noname'):
    # выводим название характеристики
    print('= {} =\n'.format(title.upper()))

    # получаем описательную статистику от pandas
    descr = series.describe()

    # выводим среднее
    mean = descr['mean']
    print('= Mean:\t{:.0f}'.format(mean))

    # выводим стандартное отклонение
    std = descr['std']
    print('= Std:\t{:.0f}'.format(std))

    # разделитель для красоты
    print('\n= = = =\n')

    # считаем интвервалы
    ## 68%
    devi_1 = [mean - std, mean + std]
    ## 95%
    devi_2 = [mean - 2 * std, mean + 2 * std]
    ## 99.7%
    devi_3 = [mean - 3 * std, mean + 3 * std]

    # выводим результат
    print('= 68% is from\t\t{:.0f} to {:.0f}'.format(devi_1[0], devi_1[1]))
    print('= 95% is from\t\t{:.0f} to {:.0f}'.format(devi_2[0], devi_2[1]))
    print('= 99.7% is from\t\t{:.0f} to {:.0f}'.format(devi_3[0], devi_3[1]))

Ну и применяем её к данным:

Мужчины | Рост

get_stats(data_male['Height'], title='Male Height')

>> 
= MALE HEIGHT =

= Mean: 175
= Std:  7

= = = =

= 68% is from       168 to 183
= 95% is from       161 to 190
= 99.7% is from     154 to 197

Мужчины | Вес

get_stats(data_male['Height'], title='Male Height')

>> 
= MALE WEIGHT =

= Mean: 85
= Std:  9

= = = =

= 68% is from       76 to 94
= 95% is from       67 to 103
= 99.7% is from     58 to 112

Женщины | Рост

get_stats(data_male['Height'], title='Male Height')

>> 
= FEMALE HEIGHT =

= Mean: 162
= Std:  7

= = = =

= 68% is from       155 to 169
= 95% is from       148 to 176
= 99.7% is from     141 to 182

Женщины | Вес

get_stats(data_male['Height'], title='Male Height')

>> 
= FEMALE WEIGHT =

= Mean: 62
= Std:  9

= = = =

= 68% is from       53 to 70
= 95% is from       44 to 79
= 99.7% is from     36 to 87

Отсюда выводы:

• Большинство мужчин: 154см–197см и 58кг–112кг.
• Большинство женщин: 141см–182см и 36кг–87кг.

Теперь осталось только применить машинное обучение к этому набору и попробовать предстазать вес по росту.

Ближайшие соседи

Алгоритм «К ближайших соседей» прост. Он существует для задач классификаций — отличить котика от собачки — и для задач регрессии — угадать вес по росту. Это то, что нам нужно!

Для регрессии он использует такой алгоритм:

• Запоминает все точки данных
• При появлении новой точки — ищет К её ближайших соседей (число К задаёт пользователь)
• Усредняет результат
• Выдаёт ответ

Для начала нужно разделить набор данных на обучающую и тестовую части и опробовать алгоритм

Экспериментируем на мужчинах

X_train, X_test, y_train, y_test = train_test_split(data_male['Height'], data_male['Weight'])

Разделили, настало время пробовать.

# Три соседа
knr3 = KNeighborsRegressor(n_neighbors=3)
knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1))
knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1))

>> 0.8298400793623182

# Пять соседей
knr5 = KNeighborsRegressor(n_neighbors=5)
knr5.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1))
knr5.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1))

>> 0.7958051642678619

# Семь соседей
knr7 = KNeighborsRegressor(n_neighbors=7)
knr7.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1))
knr7.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1))

>> 0.7769249318420969

Не будем далеко ходить и остановимся на трёх соседях. Но вопрос: сможет ли такая модель угадать мой вес?

knr3.predict([[180]])[0, 0]

>> 88.67596236265881

88кг — это очень близко. В эту секунду мой вес — 89.8кг

График предсказаний для мужчин

Время построить мою любимую часть науки — графики.

array_male = []

# доверительный интервал 99.7%
xaxis = range(154, 198)

for h in xaxis:
    ans = knr3.predict([[h]])
    array_male.append(ans[0, 0])

plt.figure(figsize=(20,10))
plt.plot(xaxis, array_male, 'r-', linewidth=4)
plt.title('Male heght-weight dependence', fontsize=30)
plt.xlabel('Height', fontsize=30)
plt.ylabel('Weight', fontsize=30)
plt.grid()
plt.savefig('plt_knn_male.png')
plt.show()

Модель и график предсказаний для женщин

X_train, X_test, y_train, y_test = train_test_split(data_female['Height'], data_female['Weight'])

knr3 = KNeighborsRegressor(n_neighbors=3)
knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1))
knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1))

>> 0.8135681584074799

array_female = []

# доверительный интервал 99.7%
xaxis = range(141, 183)

for h in xaxis:
    ans = knr3.predict([[h]])
    array_female.append(ans[0, 0])

plt.figure(figsize=(20,10))
plt.plot(xaxis, array_female, 'b-', linewidth=4)
plt.title('Female heght-weight dependence', fontsize=30)
plt.xlabel('Height', fontsize=30)
plt.ylabel('Weight', fontsize=30)
plt.grid()
plt.savefig('plt_knn_female.png')
plt.show()

Ну и конечно интересно, как выглядят эти графики вместе:

# объединение интервалов мужчин и женщин
xaxis = range(154, 183)

plt.figure(figsize=(20,10))
plt.plot(xaxis, array_male[:-15], 'r-', linewidth=4)
plt.plot(xaxis, array_female[13:], 'b-', linewidth=4)
plt.title('Together heght-weight dependence', fontsize=30)
plt.xlabel('Height', fontsize=30)
plt.ylabel('Weight', fontsize=30)
plt.grid()
plt.savefig('plt_knn_together.png')
plt.show()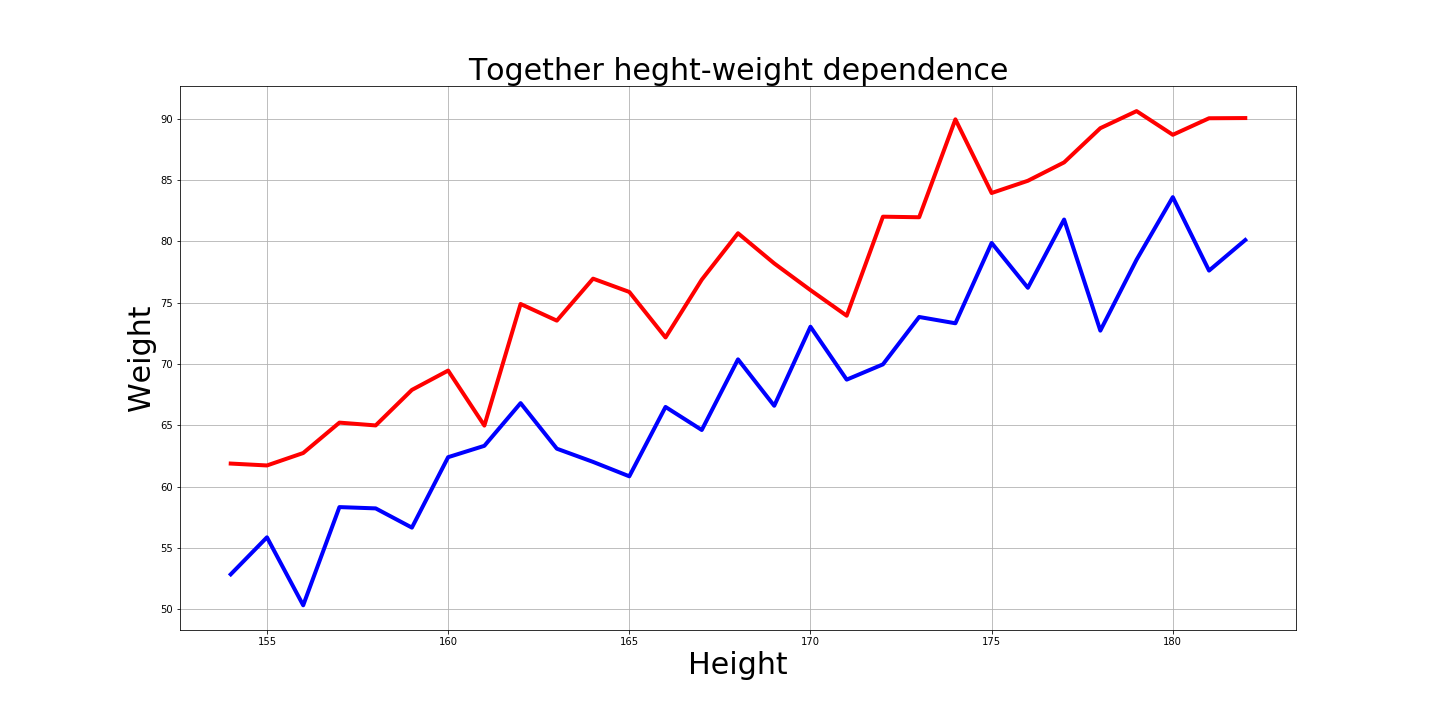

Ответы на вопросы

— В каком диапазоне вес и рост у большинства мужчин и женщин?

99.7% мужчин: от 154см до 197см и от 58кг до 112кг.
А 99.7% женщин: от 141см до 182см и от 36кг до 87кг.

— Какие они — «средний» мужчина и «средняя» женщина?

Средний мужчина — 175см и 85кг.
А средняя женщина — 162см и 62кг.

— Сможет ли простенькая модель машинного обучения «KNN» по этим данным угадать вес по росту?

Да, модель предсказала 88кг, а у меня 89.8кг.

Все, что сделал, собрал тут

Минусы статьи

• Нет описания ДатаСета. Вероятно, возраст и другие факторы у людей различались. Поэтому на веру принимать его нельзя, а ради эксперимента — пожалуйста.
• По-хорошему — нужно было сделать тест на нормальность распределения

Эпилог

Ставь лайк, если попал в 99.7% интервал