Привет, Хабр! Поиграем в судоку?

Судоку – это игра, в которой игровое поле представляет собой квадрат размером 9×9, разделённый на меньшие квадраты со стороной в 3 клетки. Таким образом, всё игровое поле состоит из 81 клетки. В них уже в начале игры стоят некоторые числа (от 1 до 9), называемые подсказками. От игрока требуется заполнить свободные клетки цифрами от 1 до 9 так, чтобы в каждой строке, в каждом столбце и в каждом малом квадрате 3×3 каждая цифра встречалась бы только один раз.

Процесс решения мы разобьём на несколько этапов:

1. Определение границ судоку и выравнивание поля (OpenCV)

2. Распознание исходных данных (подсказок) (EasyOCR)

3. Решение задачи (PuLP)

4. Отображение ответа на исходном изображении

Для решения первой задачи мы воспользуемся OpenCV.

Сначала открываем изображение и находим на нём все контуры. Для этого необходимо перевести изображение в серые тона, наложить размытие (чтобы сгладить шум) и при помощи функции порога adaptiveThreshold на изображении оставляем только главные контуры:

# Открываем изображение с судоку
img = cv2.imread('example/test.png')

# Находим контуры на изображении
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
blurry = cv2.GaussianBlur(gray, (5, 5), 5)
thresh = cv2.adaptiveThreshold(blurry, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY_INV,57,5)
cnts,_ = cv2.findContours(thresh, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
cnts = sorted(cnts, key=cv2.contourArea, reverse=True)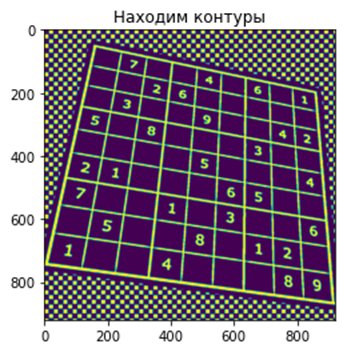

Чтобы найти на фото квадрат с судоку предположим, что он будет являться самым большим квадратом на изображении. Для этого при помощи аппроксимации контуров возьмём наибольший по площади контур с 4 сторонами и отсортируем координаты углов по часовой стрелке:

# Для поиска сетки судоку находим наибольший квадрат на изображении
location = None
for cnt in cnts:
    approx = cv2.approxPolyDP(cnt, 15, True)
    if len(approx) == 4:
        # Сортировка углов по часовой стрелке
        rect = np.zeros((4, 2), dtype = "float32")
        cutt = approx[:,0]

        diag_1 = cutt.sum(axis = 1)        
        rect[0] = cutt[np.argmin(diag_1)]
        rect[2] = cutt[np.argmax(diag_1)]

        diag_2 = np.diff(cutt, axis = 1)
        rect[1] = cutt[np.argmin(diag_2)]
        rect[3] = cutt[np.argmax(diag_2)]

        location = rect
        break

Далее создаём квадрат и при помощи getPerspectiveTransform и warpPerspective вписываем в него наш квадрат с судоку:

# Создаём квадрат 900х900
height = 900
width = 900
pts1 = np.float32([location[0], location[1], location[3], location[2]])
pts2 = np.float32([[0, 0], [width, 0], [0, height], [width, height]])

# Вписываем судоку в наш квадрат
matrix = cv2.getPerspectiveTransform(pts1, pts2)
board = cv2.warpPerspective(img, matrix, (width, height))

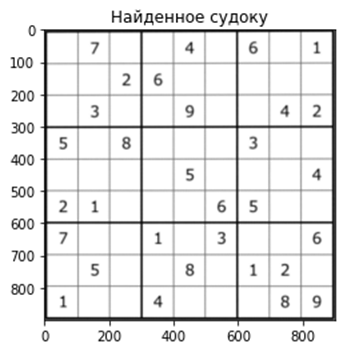
Теперь нам необходимо распознать подсказки, с чем нам поможет EasyOCR:

# Загружаем модель OCR
import easyocr
reader = easyocr.Reader(['en'])

# Создаём датафрейм и список для записи распознанных результатов
df = pd.DataFrame(index=range(1, 10), columns=range(1, 10))
sudoku_map = []

# Создаём оси для отрисовки разделённых изображений
fig, ax = plt.subplots(9, 9, figsize=(8,8))

Для будущего решения нам потребуется знать значение подсказки, его номер строки и столбца. Так как мы конвертировали изображение в размер 900х900, мы можем получить столбцы судоку просто разделив изображение на 9, а затем разделить каждый столбец на 9 для получения ячеек. Передадим модели параметр allowlist=’0123456789’, чтобы она распознавала только числа:

# Разделяем наш судоку на 9 строк и 9 столбцов и распознаём каждое значение
split = np.split(board, 9, axis=1)
for col,j  in enumerate(split):
    digs = np.split(j, 9)
    for row,d in enumerate(digs):
        # Обрежем по 10 пикселей с каждой стороны ячейки, чтобы убрать рамки
        d = d[10:90,10:90]
        cv2.copyMakeBorder(d,10,10,10,10,cv2.BORDER_CONSTANT)
        ax[row][col].imshow(d)
        ax[row][col].axis('off')
        
        # Распознаём число в ячейке и записываем его в датафрейм и список с координатами
        text = reader.readtext(d, allowlist='0123456789', detail=0)
        if len(text) > 0:
            df.iloc[row, col] = text[0]
            sudoku_map.append([text[0], str(row+1), str(col+1)])

df.fillna('', inplace=True)
df

Результат распознавания:

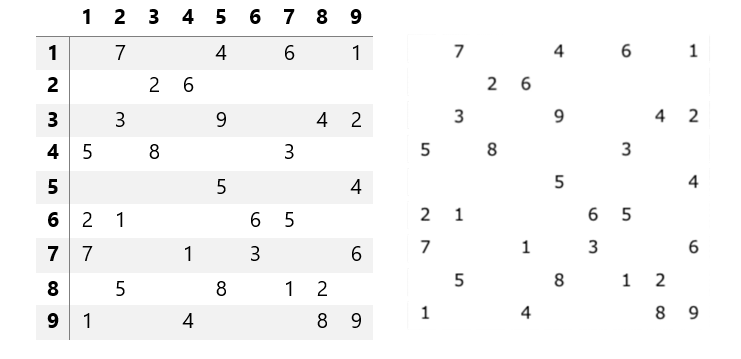
Как мы видим, все числа распознались корректно.

Остался последний этап – решить судоку. Для этого мы воспользуемся библиотекой PuLP.

PuLP – библиотека линейного программирования на Python. В нашем случае, мы будем искать оптимальное значение для каждой ячейки основываясь исключительно на ограничениях, так как целевой функции в решении судоку нет.

Создаём списки с числами от 1 до 9 (возможные значения для самой ячейки, номера столбца и номера строки) и создаём из них PuLP переменную LpVariable. В нашем случае это словарь значений от 1 до 9, в котором значением может быть 0 или 1, в зависимости от истинности утверждения. Затем объявляем задачу с любой целевой функцией (минимизация или максимизация), вместо формулы задаём 0:

# Создаём списки для перебора в Pulp
nums = [*map(str, [*range(1,10)])] # список чисел от 1 до 9 со строковым типом
rows = nums
cols = nums
vals = nums

# Создаём Pulp словарь с переменными возможных ответов
choices = LpVariable.dicts("Choice", (vals, rows, cols), 0, 1, LpInteger)

# Создаём задачу для Pulp
prob = LpProblem("Судоку", LpMaximize)
prob += 0, "Целевая функция" # Задаётся нулём, так как нас интересует только подбор значения согласно ограничениям

Добавляем в модель ограничения о подборе чисел. Для этого циклами добавляем условия, что сумма значений словаря для каждого числа, строки и столбца будет равна 1:

# Задаём ограничениями условие, что каждое число в каждой строке и каждом столбце должно повторяться не более 1 раза
for r, c in product(rows, cols):
    prob += lpSum([choices[v][r][c] for v in vals]) == 1, ""

for v, r in product(vals, rows):
    prob += lpSum([choices[v][r][c] for c in cols]) == 1, ""

for v, c in product(vals, cols):
    prob += lpSum([choices[v][r][c] for r in rows]) == 1, ""
    
# Задаём аналогичные ограничения для малых квадратов 3х3
grid = (range(3), range(3))
subs = [[(rows[3*i+k],cols[3*j+l]) for k,l in product(*grid)] for i,j in product(*grid)]
for v,s in product(vals, subs):
    prob += lpSum([choices[v][r][c] for (r, c) in s]) == 1, ""

Добавляем подсказки из ранее созданного списка с распознанными значениями. В указанных строке и столбце для значения подсказки ставим 1 (например, для 1 строки и 2 столбца проставим истину для значения 7):

# Добавляем в задачу известные значения, распознанные OCR
for num in sudoku_map:
    prob += choices[num[0]][num[1]][num[2]] == 1, ""

На этом подготовка модели завершена и для решения нам осталось добавить всего одну строчку:

# Решаем задачу
prob.solve()

Модель оптимизирует значения ячеек в судоку в соответствии с установленными ограничениями, осталось только посмотреть результат!

# Отрисовка конечного результата
fig, ax = plt.subplots(1,2, figsize=(15,15))
for a in ax:
    a.axis('off')
    a.imshow(board)

ax[0].set_title('Задача', fontsize=25)
ax[1].set_title('Решение', fontsize=25)

# Пишем решение поверх изображения
y = 50
for r in rows:
    x = 50
    for c,v in product(cols, vals):
        if choices[v][r][c].value() == 1:
            if [v,r,c] not in sudoku_map: # Пишем только подобранные значения
                ax[1].text(x,y,v, ha='center', va='center', fontsize=25, color='tab:green') 
            x += 100
    y += 100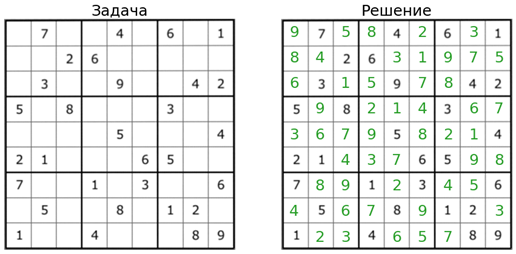

В заключение хотелось бы сказать, что в рамках поста рассмотрен только один из вариантов решения. Распознавание символов может быть ускорено при наличии GPU с поддержкой CUDA, так как EasyOCR построен на базе PyTorch, либо можно обучить свою модель. Алгоритм подстановки может быть реализован без помощи PuLP, но в рамках поста хотелось показать именно необычный способ использования данной библиотеки для линейного программирования.

Полный код можно посмотреть в репозитории