Разбираемся, что же там нового открыли в задаче о ферзях
- пятница, 8 декабря 2017 г. в 03:18:56
Пару месяцев назад появилась занятная статья с анализом классической задачи о расстановке ферзей на шахматной доске (см. детали и историю ниже). Задача невероятно известная и вся уже рассмотрена под микроскопом, поэтому было удивительно, что появилось что-то действительно новое.
Сможете поставить ещё шесть? А найти все решения?
(картинка из статьи)
Далее, к сожалению, произошла какая-то совершенно невразумительная история из цепочки вот таких вот превращений:
Стоит отметить, что пять наугад открытых ссылок на русском ещё меньше проясняли картину происходящего.
Я тут подумал — надо бы кому-то эту странную цепочку прервать и нормальным языком изложить суть событий.
О чём пойдёт речь:
Задача известна еще с древности (~ средних веков), необходимо расставить буквы таким образом, чтобы ни в одной строке и ни в одной колонке не было одинаковых, как например здесь:

Задачу придумал в 1848 году шахматный композитор Макс Беззель: суть задачи в том, чтобы расставить 8 ферзей на шахматной доске так, чтобы они не атаковали друг друга. С тех пор многие математики, например Гаусс, работали над задачей, а алгоритмисты и программисты, такие как Дейкстра, придумали множество подходов к поиску и подсчету решений.
В задаче, о которой мы будем говорить, не 8 ферзей, а N и доска, соответственно, не обычная шахматная, а NxN.
Есть три наиболее популярных постановки задачи о ферзях
Задача формулируется очень прямолинейно.
Дано: пустая доска NxN, например 8х8

(в принципе понятно, что достаточно просто указать N, но так наглядней)
Найти: расстановку максимально возможного числа ферзей
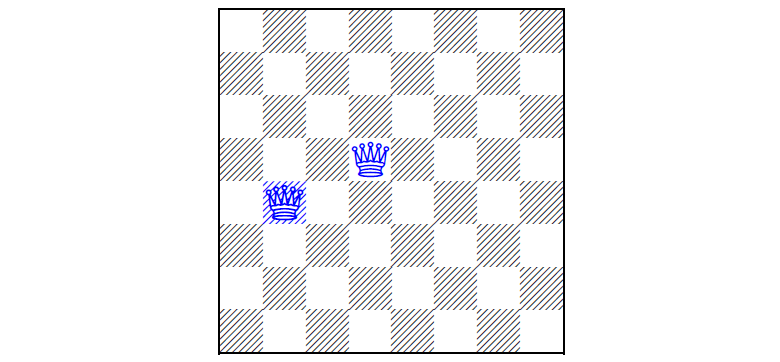
Задача ставится тоже достаточно просто:
Дано: размер пустой доски N
Найти: H число возможных расстановок N ферзей на доске
Например, размер доски N = 1, тогда число возможных расстановок H = 1.
N = 8 => H = 92.
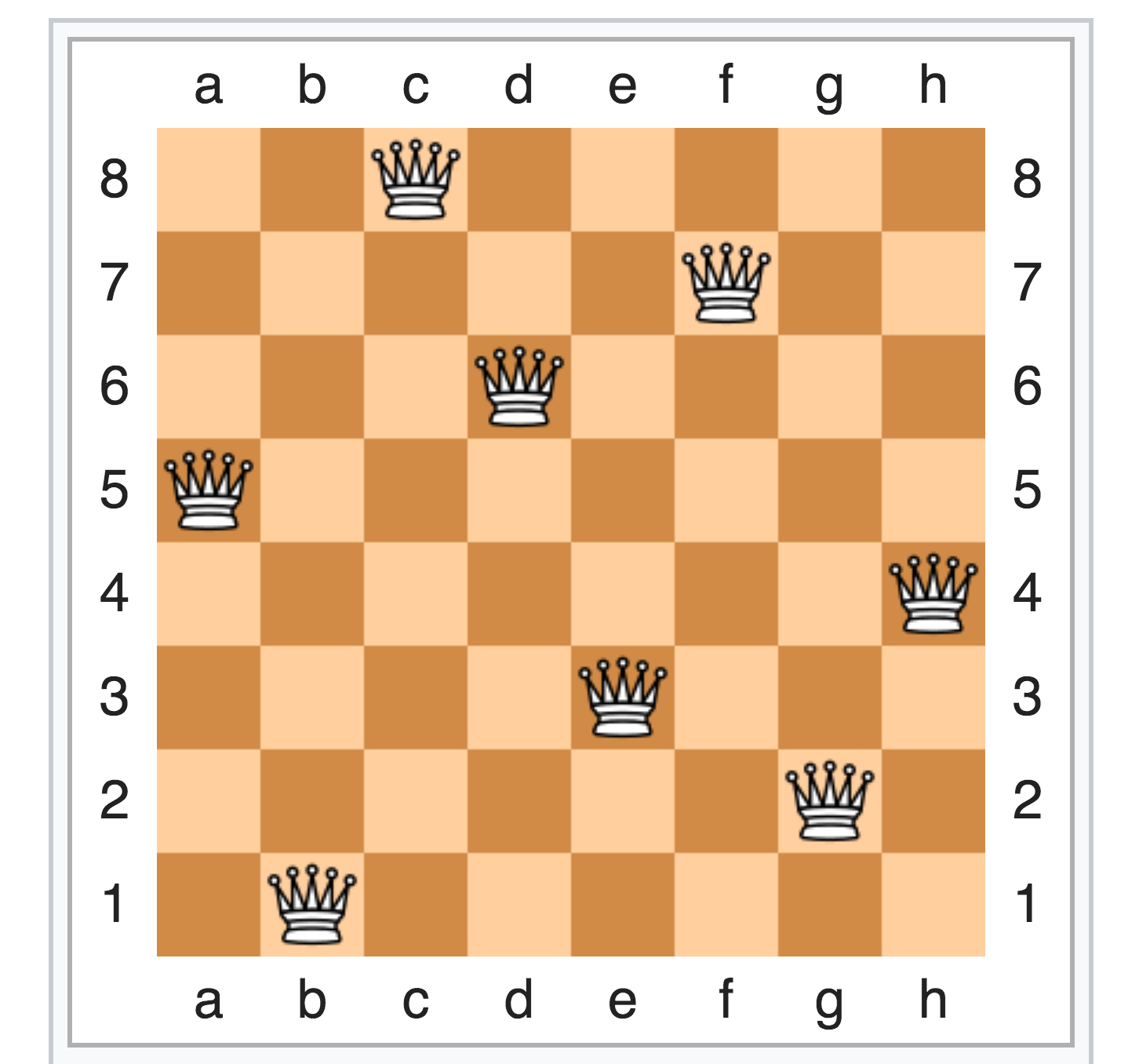
Вот тут формулировка чуть-чуть коварней:
Дано: размер доски N и M позиций уже установленных ферзей
Найти: позиции оставшихся N — M ферзей
Визуально все как на КПДВ:
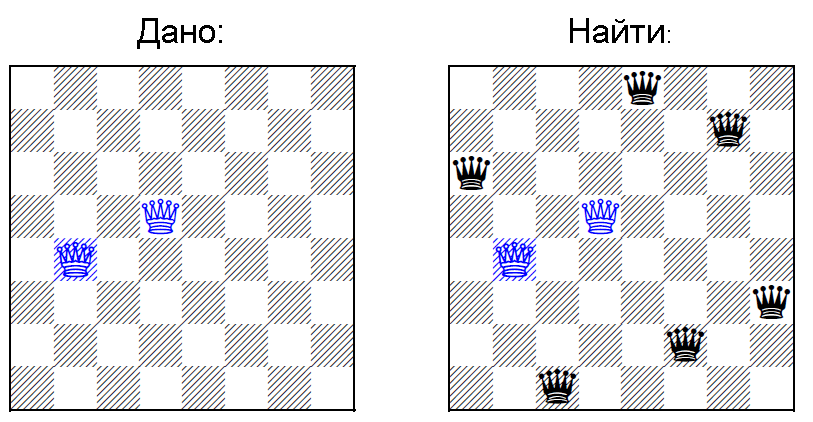
(картинка также из оригинальной статьи)
Вообще говоря, вариаций задачи больше: см. например: расстановку белых и черных ферзей
http://www.csplib.org/Problems/prob110
однако здесь мы рассматриваем только основной классический вариант.
В подобной вариации решения существенно отличаются (белые не бьют белых, а черные черных: в случае путаницы — см. комментарии тут):
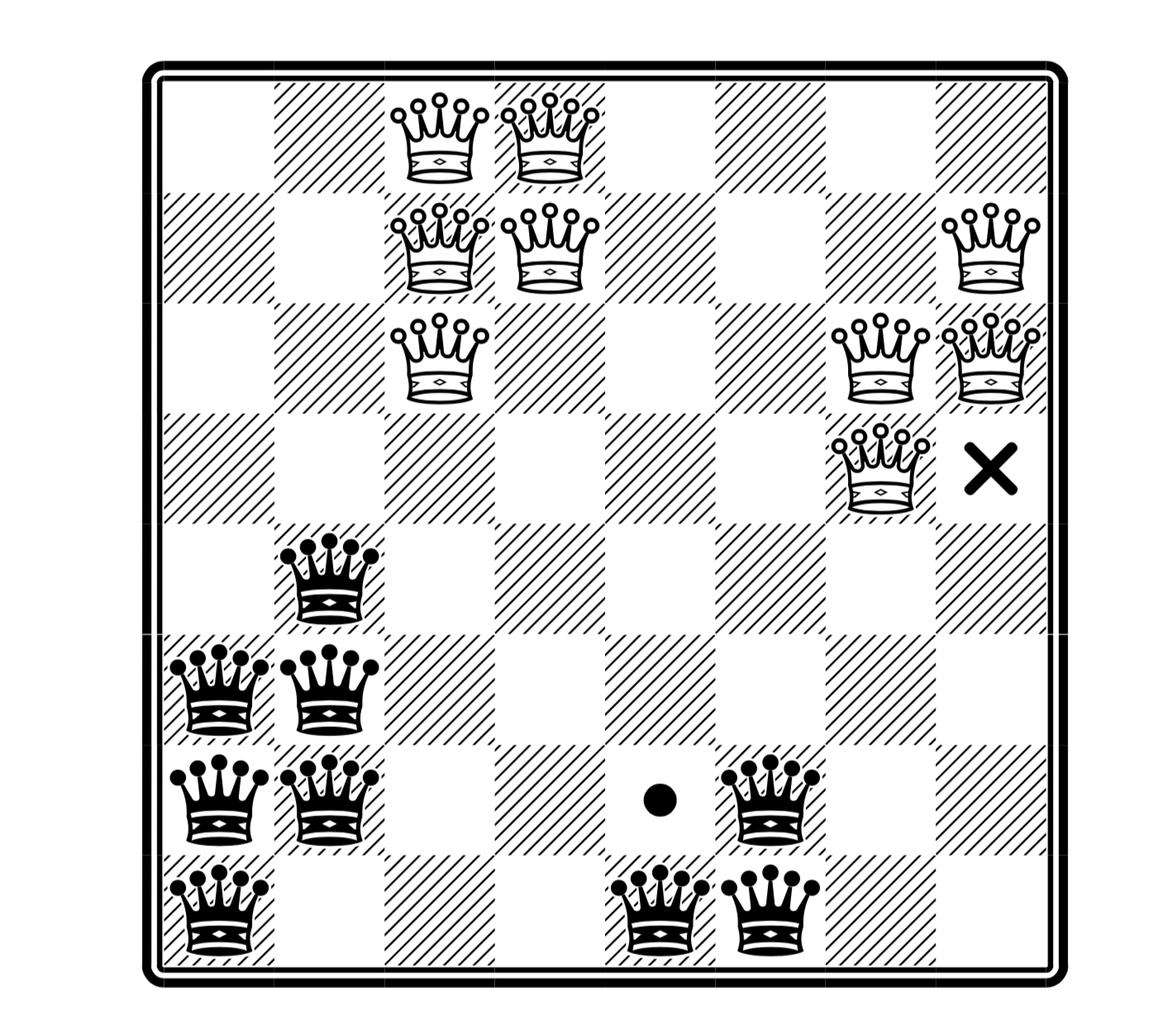
(здесь максимальное число ферзей, причем на месте крестика можно поставить белого, а на месте точке черного — но не обоих сразу; взято из статьи)
Пришло время собственно обсудить: а как это вообще все решать и насколько быстро это вообще можно сделать?
Самый интересный момент, что даже специалисты иногда путаются и думают, что для решения N-ферзей нужен комбинаторный поиск и думают, что сложность задачи выше P. Про то, что такое P и NP, когда-то уже писал на Хабре: Зачем нам всем нужен SAT и все эти P-NP (часть первая) и вторая вот тут. Однако, задача решается без перебора вариантов! Т.е., для доски любого размера можно всегда расставить ферзей один за одним лесенкой:

Существует целый ряд алгоритмов расстановки, например см. вот эту статью или даже вот тут в Вики.
Отсюда вывод, для N = 1 и N > 3 решение всегда есть (см. алго), а для N = 2 или N = 3
всегда нет (тривиально следует из доски). Это значит, что задача разрешимости для N ферзей (где нужно сказать есть решение или нет) решается тривиально за константное время (ну ок, конструктивно за линейное — расставить/проверить).
Самое время перепроверить прочитанное, читаем типичный заголовок "задачу о N ферзях признали NP-полной задачей" — у вас замироточили глаза?
Вот тут начинается самое интересное: у количества решений задачи о расстановке ферзей даже есть своё имя — "последовательность A000170". На этом хорошие новости заканчиваются. Сложность задачи: выше NP и P#, на практике это означает, что оптимальное решение — это скачать данные последовательности в словарь и возвращать нужное число. Так как для N=27 оно уже считалось на параллельном кластере сколько там недель.
Решение: выписываем табличку и по n, возвращаем а(n)
n a(n)
1: 1
2: 0
3: 0
4: 2
5: 10
6: 4
7: 40
8: 92
9: 352
10: 724
…
21: 314666222712
22: 2691008701644
23: 24233937684440
24: 227514171973736
25: 2207893435808352
26 22317699616364044
27: 234907967154122528
Однако, если у вас какая-то хитрая разновидность задачи и все-таки нужно посчитать решения (а их количество неизвестно и раньше их никто не посчитал), то лучший вариант прототипа обсуждается чуть ниже.
Тут начинается самое интересное: в чём же состоит новый результат статьи? Задача о дополнении до N ферзей — NP-полна! (Интересно, что про NP-полноту дополнения латинского квадрата было известно ещё в 1984-ом году.)
Что это означает на практике? Самый простой способ решишь эту задачу (или вдруг, если нам нужно её вариацию) — использовать SAT. Однако, мне больше нравится следующая аналогия:
SAT — это ассемблер для комбинаторных NP-задач, а Answer Set Programming (ASP) — это С++ (у ASP тоже загадочная русская душа: он временами запутан и непредсказуем для непосвященных; кстати, теория, лежащая в основе современного ASP, была придумана в 1988ом году Михаилом Гельфондом и Владимиром Лифшицем, работавших тогда в университетах Техаса и Стэнфорда соответственно).
Если говорить упрощенно: ASP — это декларативный язык программирования ограничений (constraints в англоязычной литературе) с синтаксисом Prolog. То есть мы записываем, каким ограничениям должно удовлетворять решение, а система сводит всё к варианту SAT и находит нам решение.
Детали решения здесь не столь важны, и Answer Set Programming достоин отдельного поста (который лежит у меня в черновике уже неприлично долго): поэтому разберем концептуальные моменты
% domain
row(1..n).
column(1..n).
% alldifferent
1 { queen(X,Y) : column(Y) } 1 :- row(X).
1 { queen(X,Y) : row(X) } 1 :- column(Y).
% remove conflicting answers
:- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 == Y2.
:- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 + X1 == Y2 + X2.
:- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 - X1 == Y2 - X2.Строка 1 { queen(X,Y) : column(Y) } 1 :- row(X). — называется choice rule, и она определяет, что является допустимым пространством поиска.
Последние три строки называются integrity constraints: и они определяют каким ограничениям должно удовлетворять решение: не может быть ферзя в одном и том же ряду, не может быть ферзя в одной и той же колонке (опущено, в силу симметрии) и не может быть ферзя на одной и той же диагонали.
В качестве системы для экспериментов рекомендую Clingo.
И для начала стоит посмотреть их tutorial и попочитать блог на www.hakank.org.
Безусловно, если впервые писать на ASP, то первая модель не выйдет невероятно эффективной и быстрой, но скорее всего будет быстрее перебора с возвратом, написанным на скорую руку. Однако, если понять основные принципы работы системы, ASP может стать "regexp для NP-полных задач".
Проведем простой численный эксперимент с нашей ASP моделью. Я добавил 5 коварных ферзей в модель и запустил поиск решения для N от 1 до 150 и вот, что вышло (запущено на обычном домашнем ноутбуке):
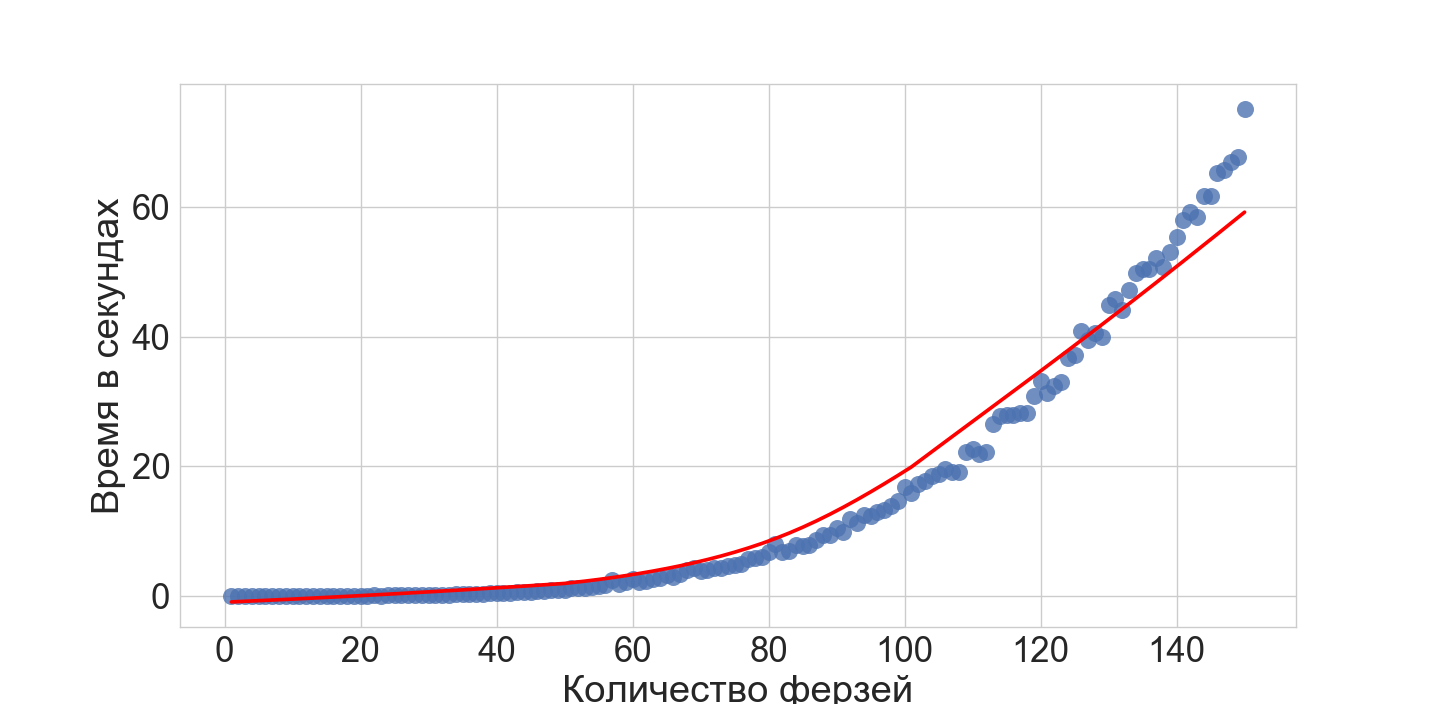
Итого, наша ASP модель примерно в течении минуты может найти решения задачи о дополнении при N <= 150 (в обычном случае). Это показывает, что система отлично подходит для прототипирования моделей сложных комбинаторных задач.