Разбираем Теорию Игр с python-библиотеками nashpy и axelrod
- воскресенье, 29 января 2023 г. в 00:40:43
Начнём с nashpy
"Камень, ножницы, бумага" - кто из нас не играл в эту игру в детстве? Но вы когда-нибудь задумывались о том, что стратегии, которые мы выбирали, на самом деле могут быть смоделированы в с помощью Теории игр?
Вы можете подумать, будто играющие в КНБ случайным образом выбирают стратегию, но на самом деле игроки часто пытаются предсказать, какой будет стратегия противника, и, соответственно, выбрать выигрышный ход.
Теория игр - это анализ стратегического взаимодействия. Теория игр построена на анализе и моделировании стратегий и результатов их применения на основе определенных правил в игре из двух или более игроков. Она имеет широкое применение в анализе политических сценариев, логических салонных игр, ситуаций в бизнесе, а также для наблюдения за экономическим поведением.
Сегодня я постараюсь объяснить некоторые понятия теории игр простыми словами, используя игры для 2-х игроков. Вы также узнаете, как решать эти игры с помощью python-библиотеки nashpy. Вот что мы рассмотрим:
Матрица выплат в игре
Что такое доминирующая стратегия
Равновесие Нэша
Чистые и смешанные стратегии
Решение с использованием python
Некоторые ограничения равновесия Нэша
Эффективность Парето
Игра в дилемму заключенного и некоторые практические приложения
Рассмотрим игру для 2 игроков - игрок A и игрок B, приведенную на рис. 1. У каждого игрока есть 2 стратегии - игрок A может выбрать верхний или нижний вариант, а игрок B - левый или правый. Приведенная выше матрица называется "матрицей выплат" (матрицей выигрышей, платежной матрицей).
Игрока A назовем игроком ряда, а игрока Б - игроком столбца. Цифры, выделенные красным цветом обозначают выплаты игрока A, а цифры голубым цветом обозначают выплаты игрока B. Например, если игрок A играет в нижний ряд, а игрок B играет в левый столбец, то как вы думаете, каковы будут выплаты?
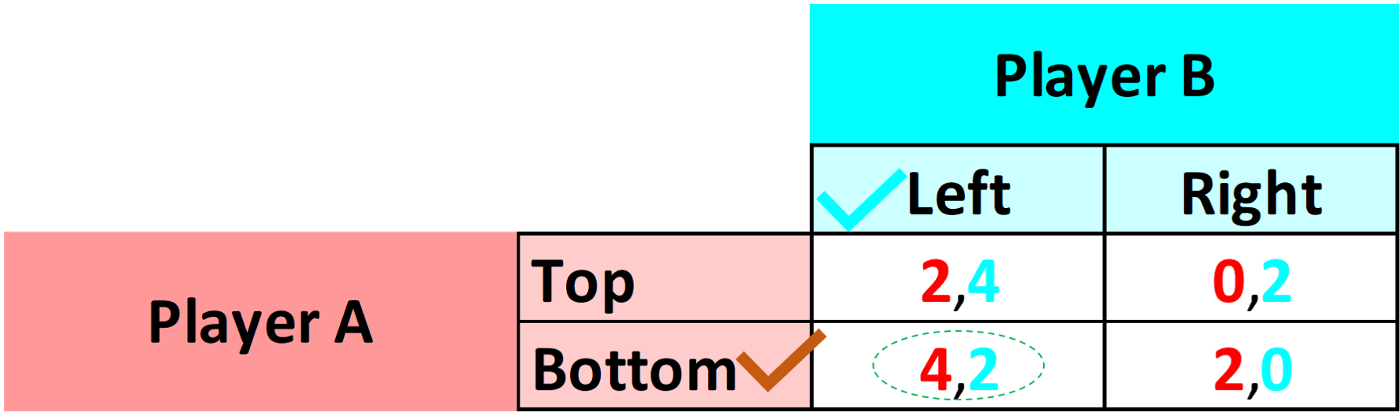
Выплата игроку A составит 4, а игроку B - 2, как вы можете видеть на рис. 2. У этой конкретной игры есть очень простое решение. Для игрока А всегда лучше играть в нижний ряд, потому что его выигрыши (4 или 2) от этой стратегии всегда больше, чем в верхнем ряду (2 или 0). Аналогично, для игрока B всегда лучше играть "слева", потому что его выплаты (4 или 2) всегда больше, чем в правом ряду (2 или 0). Следовательно, стратегия равновесия заключается в том, чтобы игрок A играл "внизу", а игрок B играл "слева". Это подводит нас к концепции доминирующей стратегии.
Доминирующая стратегия: Существует только одна оптимальная стратегия для каждого игрока, независимо от того, какую стратегию принимает другой игрок. Какой бы выбор ни делал B, A всегда должен выбирать нижний ряд, и на любой выбор игрока A другой игрок, B всегда должен выбирать левый столбец.
Равновесие Нэша
Рассмотрим игру №2 :
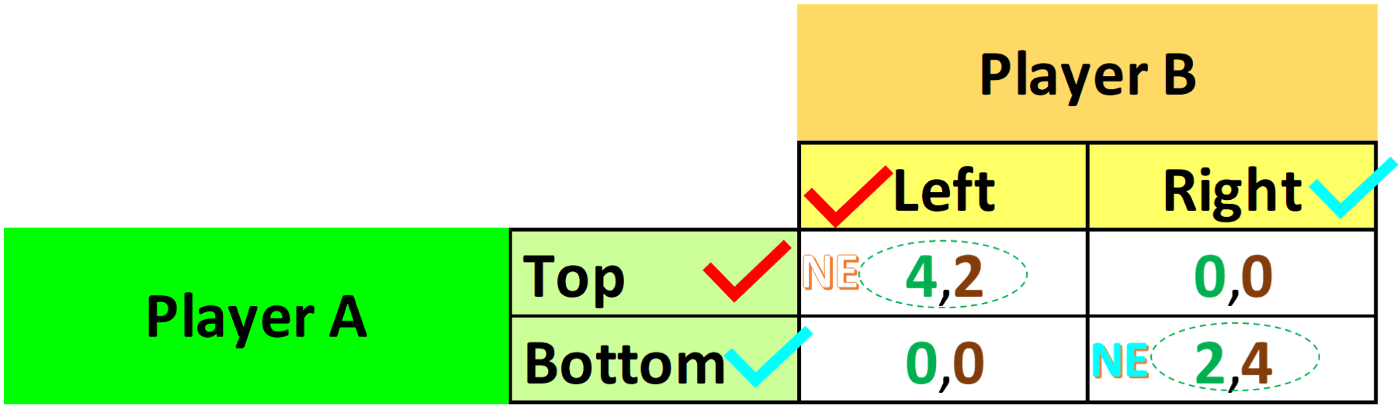
Примечание: Выплаты игрока A - зеленым цветом, а игрока B - коричневым.
В этой игре, если игрок B выбирает левый столбец, то выплаты игрока A составляют либо 4, либо 0. Если же игрок B выбирает правый столбец, выплаты игрока A составляют 0 или 2. Следовательно, если B выбирает левый, A должен выбрать верхнюю строку, а если B выбирает правый, то A должен выбрать нижнюю. То есть оптимальный выбор A зависит от того, какой выбор делает B.
Пара стратегий является равновесием Нэша (NE), если оптимальный выбор игрока A при выборе игрока B совпадает с оптимальным выбором игрока B при выборе игрока A. Проще говоря, изначально ни один из игроков не знает, что будет выбирать другой игрок. Следовательно, NE - это пара вариантов/стратегий/ожиданий, когда ни один из игроков не захочет менять свое поведение даже после раскрытия стратегии/выбора другого игрока.
В этой игре стратегия (сверху, слева) - это равновесие Нэша, потому что если A выбирает верх, то лучше всего для B выбрать лево, потому что его выигрыш слева равен 2, а не 0. Аналогично, если B выберет левый столбец, то лучший выбор для A - выбрать верхнюю строку, потому что он получит более высокую выплату 4, а не 0, как при выборе нижней.
Итак, может ли быть множественное равновесие Нэша? Ответ - Да. В этой игре мы только что увидели, на самом деле у нас есть 2 равновесия Нэша - стратегия (нижняя строка, правый столбец) также является NE, потому что если A выбирает нижнюю строку, B должен выбрать правый столбец и наоборот.
Теперь давайте попробуем выяснить равновесие Нэша для этой игры (Игра 2) и предыдущей, т.е. Игры 1 с использованием nashpy в python.
Игра 1 с использованием python:
import nashpy
# Create the game with the payoff matrix
A = np.array([[2,0],[4,2]]) # A is the row player
B = np.array([[4,2],[2,0]]) # B is the column player
game1 = nash.Game(A,B)
game1Bi matrix game with payoff matrices:
Row player:
[[2 0]
[4 2]]
Column player:
[[4 2]
[2 0]]Теперь определим равновесие Нэша:
# Find the Nash Equilibrium with Support Enumeration
equilibria = game1.support_enumeration()
for eq in equilibria:
print(eq)(array([0., 1.]), array([1., 0.]))Поскольку у игрока есть 2 стратегии - у игрока A (верхняя строка, нижняя строка), а у игрока B (слева, справа), то вывод можно интерпретировать следующим образом:
Игрок А выбирает стратегию 2, т.е. «Внизу», поскольку «1» на второй позиции массива, а игрок B выбирает стратегию 1, т.е. "Слева", поскольку "1" в первой позиции массива. Следовательно, как мы видели ранее, стратегия (внизу, слева), это исход этой игры.
Игра 2 с использованием python:
Используя ту же логику, что и выше, давайте вычислим равновесия Нэша для игры 2.
# Create the payoff matrix
A = np.array([[4,0],[0,2]]) # A is the row player
B = np.array([[2,0],[0,4]]) # B is the column player
game2 = nash.Game(A,B)
print(game2)
# Find the Nash Equilibrium with Support Enumeration
equilibria = game2.support_enumeration()
for eq in equilibria:
print(eq)(array([1., 0.]), array([1., 0.]))
(array([0., 1.]), array([0., 1.]))
(array([0.66666667, 0.33333333]), array([0.33333333, 0.66666667]))Здесь мы видим 3 строки вывода, давайте возьмем каждую строку и поймем, что она означает:
У игрока A есть стратегии (сверху, снизу), а у игрока B есть стратегии (слева, справа)
Строка 1: "(массив([1., 0.]), массив([1., 0.])) "
Интерпретация: Это первое равновесие Нэша (сверху, слева). Игрок А выбирает стратегию 1, т.е. «Верх», так как «1» на первой позиции первого массива, а игрок B выбирает стратегию 1, т.е. "Слева", так как "1" в первой позиции второго массива.
Строка 2: "(массив([0., 1.]), массив([0., 1.])) "
Интерпретация: Это второе равновесие Нэша (внизу, справа). Игрок А выбирает стратегию 2, т.е. «Внизу», поскольку «1» на второй позиции первого массива, а игрок B выбирает стратегию 2, т.е. "Справа", поскольку "1" во второй позиции второго массива.
Но у нас также есть 3-я линия, так почему же мы получили еще один результат? Чтобы понять это, позвольте мне представить смешанные стратегии.
Стратегии, которые мы обсуждали выше в игре 1 и 2, называются "Чистые стратегии". Но мы, люди, обычно не делаем один выбор навсегда, не так ли? Таким образом, игроки могут рандомизировать свои стратегии. Вероятности могут быть присвоены каждой чистой стратегии, и игроки могут выбирать стратегии в соответствии с назначенной ей вероятностью. Следовательно, строку 3 вывода игры 2 можно интерпретировать так:
Строка 3: "(массив([0.66666667, 0.33333333]), массив([0.33333333, 0.66666667])) "
Интерпретация: Игрок А использует стратегию 1, т.е. "Верх" 66,67% времени и стратегию 2, т.е. "Нижняя строка" 33,33% времени, в то время как игрок B использует стратегию 1, т.е. "Лево" 33,33% времени и стратегию 2, т.е. "Право" 66,67% от всех ходов.
Логично же, что игрок A должен присвоить более высокую вероятность стратегии "Верх", а игрок B - "Право", потому что это дает им более высокие выигрыши.
Это равновесие представляет собой смешанную стратегию равновесия Нэша и определяется так:
"Каждый игрок выбирает оптимальную "частоту", с которой можно играть свои стратегии, учитывая выбор частоты другого игрока"
Как мы рассчитываем полезность/выплаты игрока A и игрока B в смешанной стратегии равновесия Нэша?
Общая математическая формулировка дается следующим образом:
Рассмотрим игру
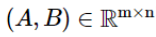
σr и σc являются смешанными стратегиями для игроков строк и столбцов (игроков A и B соответственно).
Далее, полезность/ выигрыш/ оплата для игрока ряда (A) составляет:
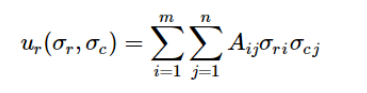
и полезность/ выигрыш/ выплата для игрока столбца (B) составляет:
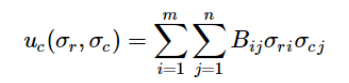
Вероятность нахождения в данной ячейке (одновременного выбора соответствующих ячейке вариантов стратегии со стороны игрока A и B) представляет собой произведение вероятностей выбора соответствующей строки и столбца со стороны игрока А и игрока B (см далее в примере расчёта):
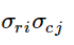
Значение ячейки равно выигрышу для А или B:
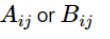
В нашем случае полезность для A будет следующей:
0.67*0.33*4 + 0.33*0.67*0 + 0.33*0.67*0 + 0.33*0.67*2 = 1.3266
и для B это будет:
0.33*0.67*2 + 0.67*0.33*0 + 0.33*0.67*0 + 0.67*0.33*4 = 1.3266
Давайте вычислим это в python:
# Calculate Utilities
sigma_r = np.array([.67,.33])
sigma_c = np.array([.33,.67])
pd = nash.Game(A, B)
pd[sigma_r, sigma_c]array([1.3266, 1.3266])Отлично, это полностью соответствует нашим расчетам выше.
Существует несколько проблем или ограничений равновесия Нэша:
Множественные равновесия Нэша: Как показано в игре 2, может быть несколько равновесий Нэша, поэтому в этом случае не существует уникального решения.
Нет равновесия Нэша: Есть игры, в которых нет равновесия Нэша. Рассмотрим игру 3 ниже:
Примечание: Выплаты игрока A - зеленым цветом, а игрока B - коричневым.
Здесь, если игрок A играет Верх, то игрок B должен играть Лево (выплата 0 > выплата -2). Если игрок B играет Лево, то игрок A должен играть Низ (выплата 2 > выплата 0). Если игрок A играет Низ, то игрок B должен играть Право (выплата 6 > выплата 0), а если игрок B играет Право, то игрок A должен играть Верх (выплата 0 >выплата -2). Следовательно, в этой игре нет равновесия Нэша в чистой стратегии.
3. Равновесие Нэша не обеспечивает эффективные результаты Парето:
Давайте проиллюстрируем это, рассмотрев одну из самых известных игр под названием "Дилемма заключенного".
Но до этого определим эффективность Парето в этом контексте:
Эффективность Парето - это ситуация, когда ни один игрок не может улучшить свое положение, не ухудшив положение хотя бы одного игрока.
Теперь вернемся к дилемме заключенного. Два заключенных, обвиняются в преступлении, и их допрашивают в отдельных комнатах. У каждого из них есть 2 стратегии -
а) Признаться в преступлении - Признаться (Confess)
б) Отказаться признаваться в причастности - Отрицание (Deny)
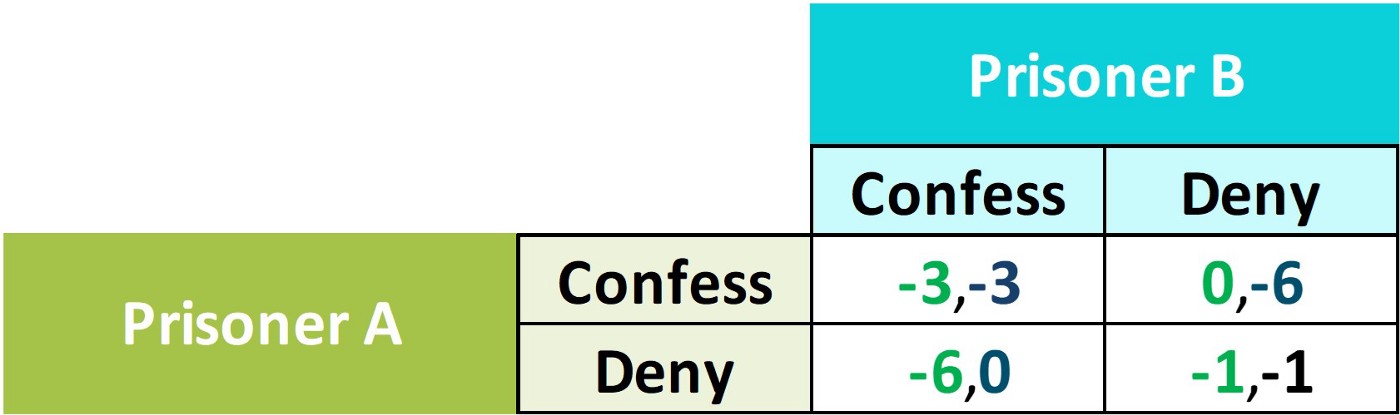
Если бы только один заключенный признался, то он бы получил снисхождение (пошёл на сделку со следствием), а другой заключенный был бы приговорен к отбыванию 6 месяцев в тюрьме. Однако, если оба отрицают преступление, то им нужно будет отбыть по 1 месяцу в тюрьме. Если они оба признаются, то каждый из них должен будет отбыть по 3 месяца в тюрьме. Матрица выплат показана выше для 4-й игры.
Теперь давайте рассмотрим полезности и стратегии, которые должен выбрать каждый заключенный.
Если заключенный А признается, то заключенному B тоже лучше признаться, потому что его полезность -3 больше, чем -6. Если заключенный А отрицает, то заключенному B лучше признаться, потому что его полезность 0 > -1, и он может выйти. Следовательно, в обоих случаях, независимо от того, что делает заключенный Б, заключенному А лучше всегда признаваться.
Та же логика применима и к заключенному Б. Таким образом, (Признание, Признание) - это равновесие Нэша в этой игре. Это также доминирующая равновесная стратегия, потому что каждый заключенный имеет оптимальную стратегию, независимую от другого игрока.
Однако здесь есть подвох. Эта стратегия неэффективна по Парето, как мы проиллюстрируем ниже:
Если бы оба заключенных могли доверять друг другу (они не могут общаться друг с другом и координировать свои действия, потому что они находятся в разных комнатах и им не разрешается говорить) и договориться все отрицать, то им обоим было бы лучше. В этом случае их выплаты будут (-1, -1). Следовательно, с этой точки зрения стратегия (Отрицать, Отрицать) наиболее эффективна, потому что нет другой стратегии, которая дает в сумме для обоих больший выигрыш.
Расчет дилеммы заключенного на python:
Вот код, который вы можете использовать для решения игры:
# Create the payoff matrix
A = np.array([[-3,0],[-6,-1]]) # A is the row player
B = np.array([[-3,-6],[0,-1]]) # B is the column player
game4 = nash.Game(A,B)
game4
# Find the Nash Equilibrium with Support Enumeration
equilibria = game4.support_enumeration()
for eq in equilibria:
print(eq)Bi matrix game with payoff matrices:
Row player:
[[-3 0]
[-6 -1]]
Column player:
[[-3 -6]
[ 0 -1]]
(array([1., 0.]), array([1., 0.]))Как вы можете видеть, стратегия 1, т.е. (Признаться, Признаться) для обоих заключенных - это равновесие Нэша.
Применение дилеммы заключенного
Игра в дилемму заключенного имеет много применений в экономике, политике, промышленности и других бизнес-решениях. Например: есть две фирмы - фирма A и фирма B, которые являются лидерами на рынке, скажем, авиационной отрасли. Пусть стратегия 1 (признаться) означает «сохранять цену авиабилета неизменной», а стратегия 2 (отрицание) как «снизить цену авиабилета». Снижение цены может быть попыткой заполнить пустые места и захватить рынок. Если фирма A сохранит цену авиабилета неизменной, то она проиграет фирме B, которая может снизить цену и захватить рынок. В последовательной игре это может привести к ценовой войне. Однако, если обе фирмы образуют картель и решат сохранить цены без изменений, то обеим будет лучше.
Резюме:
Мы обсудили концепции теории игр с некоторыми известными играми. Ходы в них делались одновременно.
Далее мы изучим последовательные игры, в которых ходы делаются поочередности, и есть несколько раундов, и как из-за этого могут измениться результаты игры.
Вот еще одна известная игра "Hawk-Dove" (Ястреб-Голубь). Верный своему названию "ястреб" использует агрессивную стратегию, а "голубь" - к пассивную.
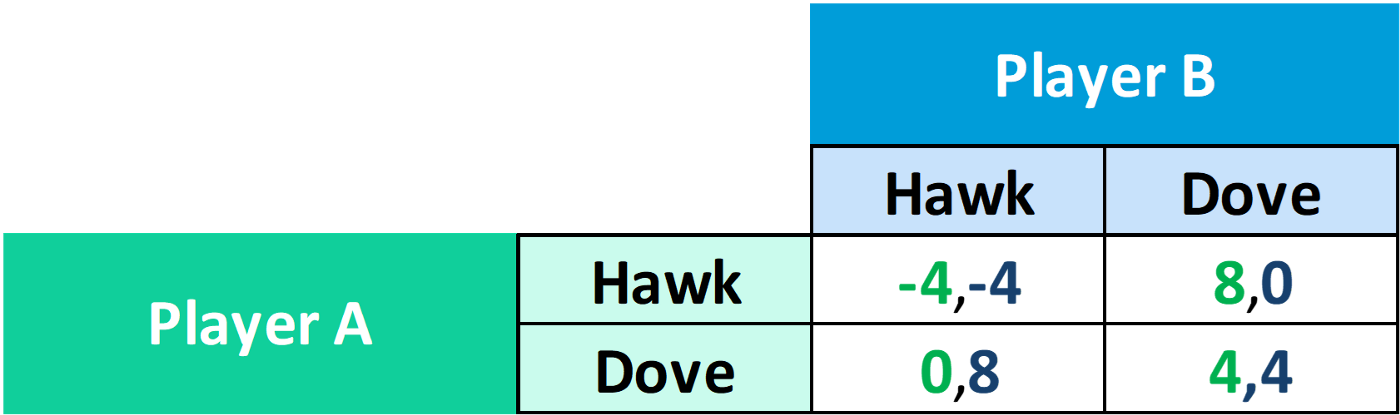
Попробуйте сыграть в неё сначала в уме, а потом с использованием nashpy, и напишите в комментариях, каковы будут результаты и почему.
Полный код доступен на Github.
Продолжим с axelrod
Теперь мы поговорим о повторяющихся играх и о том, как это может повлиять на ход игры, особенно в дилемме заключенного, обсуждавшийся выше.
Вот наш план:
Введем новые условия в стратегию дилеммы заключенного
Дилемма заключенного: играем конечное количество игр
Дилемма заключенного: играем бесконечное количество игр
Матрица выплат в двух случаях
Визуализация игры с использованием sparklines
Итак, вернемся к дилемме заключенного. В таблице 1 показана матрица выплат. Мы принимаем матрицу выплат по умолчанию в соответствии с пакетом Axelrod:
В нашем предыдущем разборе у заключенных было 2 стратегии (Признание, Отрицание), а равновесием Нэша было (Признание, Признание). Это будет доминирующей равновесной стратегией.
Обратите внимание, что стратегия "Признание" также является своего рода "предательской" (Defect) стратегией, а стратегия "Отрицание" фактически означает "сотрудничество" (Cooperate).
В предыдущем случае игроки делали выбор только один раз, и игра была сыграна один раз.
Теперь, когда игру можно сыграть несколько раз, каждому игроку доступен ряд новых стратегических возможностей. Стратегия зависит от того, будет ли игра сыграна конечное или бесконечное число раз. Давайте рассмотрим оба случая по порядку.
Случай 1: Игра играется конечное количество раз (скажем, 10)
Давайте рассмотрим последний раунд, т.е. раунд 10 - это последний раз, когда игра будет сыграна, поэтому нет смысла сотрудничать, и, следовательно, каждый игрок скорее будет "предателем", т.е. признается.
Теперь давайте рассмотрим 9-й раунд: мы только что увидели, что в 10-м раунде игроки не сотрудничают, так почему же они должны сотрудничать в 9-м раунде? Если предположить, что игрок A сотрудничает, то игрок B может предать, используя хорошие побуждения игрока A, и выйти из заключения. (Ведь в следующем раунде его все рано накажут - там всем выгодно быть "предателями" - прим. переводчика). Каждый игрок будет размышлять таким образом, и каждый будет склоняться к "предательству", т.е. стратегии Признаться. Эта логика может быть применена далее ко всем предыдущим раундам.
Следовательно, если игра сыграна конечное/фиксированное количество раз, то каждый игрок будет "предавать" в каждом раунде. Игроки сотрудничают, надеясь, что это вызовет сотрудничество в будущем. Но если нет шансов на будущую игру, нет необходимости сотрудничать сейчас.
Следовательно, результат будет (Признаться, Признаться), как и раньше, когда игра была сыграна только один раз.
Давайте проиллюстрируем это с python. Теперь мы будем использовать пакет Axelrod для повторяющихся игр.
Обратите внимание, что стратегия сотрудничества в пакете Axelrod обозначается как "C", а стратегия перебежчика - как "D".
import axelrod as axl
players = (axl.Defector(), axl.Defector())
match1 = axl.Match(players, turns =10)
match1.play()[(D, D),
(D, D),
(D, D),
(D, D),
(D, D),
(D, D),
(D, D),
(D, D),
(D, D),
(D, D)]Как видите, в конечной игре игроки будут "предавать" во всех раундах.
Случай 2: Игра продолжается бесконечное количество раз
Стратегии меняются, когда в игру играют бесконечное количество раз. Если игрок A отказывается сотрудничать в одном раунде, то игрок B может отказаться от сотрудничества в следующем раунде. Угроза отказа от сотрудничества заставит игроков прибегнуть к сотрудничеству и играть в соответствии с эффективной стратегией Парето, т.е. Отрицать.
Роберт Аксельрод продемонстрировал это с помощью серии экспериментов, в которых различные стратегии были протестированы на игроках в турнире.
Победившей стратегией/комбинацией ходов оказалась "Око за око", поскольку она давала самую высокую отдачу для игрока.
В первом раунде Игрок А сотрудничает и играет в стратегию "Отрицание". В каждом последующем раунде Игрок A сотрудничает, если Игрок B сотрудничал в предыдущем раунде, и признается ("предает"), если Игрок B признавался в предыдущем раунде. Таким образом, стратегия "Око за око" означает, что игрок A должен поступать так же, как игрок B поступал в предыдущем раунде.
Эта стратегия работает, потому что она дает немедленное наказание за "предательство" и немедленное вознаграждение за сотрудничество. Это в конечном итоге может привести к эффективному устойчивому результату по Парето (Отрицать, Отрицать).
Давайте проиллюстрируем это в python:
Для примера давайте сыграем в игру 20 раз. Игрок A играет в стратегию "око за око", а игрок B пусть выбирает ходы случайным образом.
players = (axl.TitForTat(), axl.Random())
match2 = axl.Match(players, turns =20)
match2.play()[(C, D),
(D, D),
(D, D),
(D, D),
(D, C),
(C, C),
(C, D),
(D, D),
(D, C),
(C, C),
(C, D),
(D, C),
(C, D),
(D, C),
(C, C),
(C, D),
(D, C),
(C, C),
(C, C),
(C, C)]Как видите, игра сходится с 18-го раунда, когда оба игрока начинают сотрудничать и играют (Отрицать, Отрицать), чем и достигается эффективный результат по Парето.
Выгоды игроков и визуализация хода игры
Теперь мы рассмотрим выигрыши в течение игры, а также визуализируем игру с помощью Sparklines.
Выплаты, установленные по умолчанию в библиотеке Axelrod следующие:
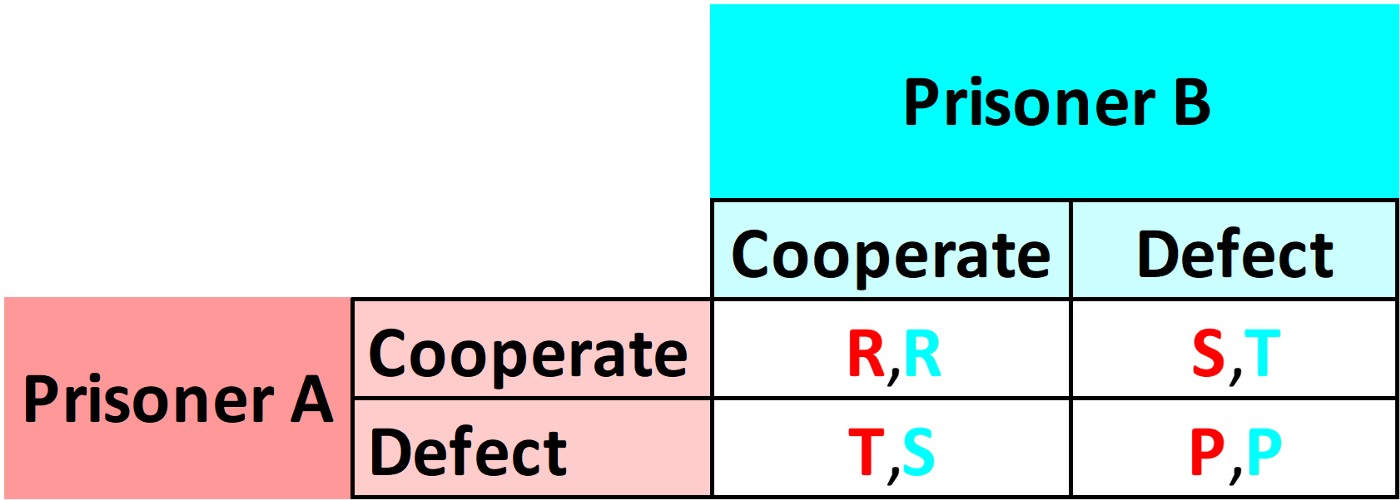
Где
R: Reward, Награда (значение по умолчанию в библиотеке: 3)
P: Punishment, Наказание (значение по умолчанию в библиотеке: 1)
S: Sucker/Loss, Простофиля/Потеря (значение по умолчанию в библиотеке: 0)
T: Temptation, Соблазн (значение по умолчанию в библиотеке: 5)
Это приведет к следующей матрице:
Выплаты при выборе в первом случае (10 раундов):
Давайте рассчитаем выплаты в первом случае:
match1.game
# Scores of a match
match1.scores()[(1, 1),
(1, 1),
(1, 1),
(1, 1),
(1, 1),
(1, 1),
(1, 1),
(1, 1),
(1, 1),
(1, 1)]Поскольку игроки всегда признаются, выплата будет (1,1), т.е. по 1 каждому игроку.
Результат матча также можно рассматривать как линию, где сотрудничество отображается как сплошной блок, а "предательство" - как пустое пространство (пробел).
Первый ряд для игрока A, а второй ряд для игрока B.
print(match1.sparklines())В этом случае вывод пуст (пробелы), потому что игроки всегда играют в "предателя". Проверьте это в python.
Вариант 2 (20 игр, один из игроков играет в "око за око"):
match2.scores()[(0, 5),
(1, 1),
(1, 1),
(1, 1),
(5, 0),
(3, 3),
(0, 5),
(1, 1),
(5, 0),
(3, 3),
(0, 5),
(5, 0),
(0, 5),
(5, 0),
(3, 3),
(0, 5),
(5, 0),
(3, 3),
(3, 3),
(3, 3)]Видно, что выплаты сходятся к (3,3).
Теперь визуализируем этот результат игры с помощью Sparklines:
print(match2.sparklines())
█ ██ ██ █ ██ ███
██ ██ █ ██ ████Резюме:
Мы обсудили, как исход игры "дилемма заключенного" меняется в повторяющихся играх и как отличаются результаты, если сыграно конечное количество раундов против бесконечного количества раундов.
Полный код доступен на Github.
P.S.: Посмотрите на результаты ниже и предположите, какая стратегия была выбрана каждым игроком?
████████████████
█ █ █ █ █ █ █ █Дополнительный бонус от переводчика:
В библиотеке axelrod содержится набор из более чем 230 стратегий для игры в дилемму заключенного. Обратите внимание, как задавались стратегии игроков (первая axl.TitForTat() означает "око за око", вторая axl.Random() - случайный выбор):
players = (axl.TitForTat(), axl.Random()) Здесь будут постепенно выкладываться все стратегии и примеры соревнований между ними. Начнем с базовых:
import axelrod as axl
axl.basic_strategies[axelrod.strategies.alternator.Alternator,
axelrod.strategies.titfortat.AntiTitForTat,
axelrod.strategies.titfortat.Bully,
axelrod.strategies.cooperator.Cooperator,
axelrod.strategies.cycler.CyclerDC,
axelrod.strategies.defector.Defector,
axelrod.strategies.titfortat.SuspiciousTitForTat,
axelrod.strategies.titfortat.TitForTat,
axelrod.strategies.memoryone.WinShiftLoseStay,
axelrod.strategies.memoryone.WinStayLoseShift]Все стратегии будут играть 50 игр против классической оптимальной "око за око" (стратегия в пером ряду, око за око - во втором)
Alternator
Alternator - игрок, чередующий сотрудничество и "предательство", начинает всегда с сотрудничества.
import axelrod as axl
players = (axl.Alternator(), axl.TitForTat())
match = axl.Match(players, turns =50)
match.play()
print(match.sparklines())█ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █
██ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █AntiTitForTat
AntiTitForTat - стратегия, при которой игрок ходит противоположно предыдущему ходу противника. Это выглядит как стратегия "Хулиган" (Bully), за исключением того, что первым шагом является Сотрудничество.
import axelrod as axl
players = (axl.AntiTitForTat(), axl.TitForTat())
match = axl.Match(players, turns =50)
match.play()
print(match.sparklines())█ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██
██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██Bully
Bully - Игрок, который ведет себя противоположно принципу "Око за око", включая первый ход. Начинает с "предательства", а затем делает ход, противоположный предыдущему ходу противника. Это полная противоположность "Око за око", также в литературе известен как "Хулиган".
import axelrod as axl
players = (axl.Bully(), axl.TitForTat())
match = axl.Match(players, turns =50)
match.play()
print(match.sparklines()) ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██
█ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ Cooperator
Cooperator - Игрок, который всегда только сотрудничает.
import axelrod as axl
players = (axl.Cooperator(), axl.TitForTat())
match = axl.Match(players, turns=50)
match.play()
print(match.sparklines())██████████████████████████████████████████████████
██████████████████████████████████████████████████
CyclerDC
CyclerDC - Циклически чередует D, C, то есть "предательство" и сотрудничество.
import axelrod as axl
players = (axl.CyclerDC(), axl.TitForTat())
match = axl.Match(players, turns=50)
match.play()
print(match.sparklines()) █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █
█ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ Defector
Defector - "Предатель", всегда.
import axelrod as axl
players = (axl.Defector(), axl.TitForTat())
match = axl.Match(players, turns=50)
match.play()
print(match.sparklines())█
SuspiciousTitForTat
SuspiciousTitForTat - Вариант "Око за око", который начинает с "предательства".
import axelrod as axl
players = (axl.SuspiciousTitForTat(), axl.TitForTat())
match = axl.Match(players, turns=50)
match.play()
print(match.sparklines()) █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █
█ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ █ TitForTat
TitForTat - Око за око. Игрок начинает с сотрудничества, а затем повторяет предыдущее действие противника.
Эта стратегия была названа "самой простой" стратегией, представленной на первом турнире Аксельрода. Она победила.
import axelrod as axl
players = (axl.TitForTat(), axl.TitForTat())
match = axl.Match(players, turns=50)
match.play()
print(match.sparklines())██████████████████████████████████████████████████
██████████████████████████████████████████████████WinShiftLoseStay
WinShiftLoseStay - "выиграл - меняй, проиграл - остановись" также называется обратной стратегией Павлова (Reverse Pavlov).
Начинает с "предательства", если предыдущий раунд (Сотрудничество, Сотрудничество) либо (Предательство, Предательство), то есть стратегии совпали, то Предать в данном ходе. Иначе - Сотрудничество.
import axelrod as axl
players = (axl.WinShiftLoseStay(), axl.TitForTat())
match = axl.Match(players, turns=50)
match.play()
print(match.sparklines()) ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ █
█ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ ██ WinStayLoseShift
WinStayLoseShift - "выиграл - продолжай так же, проиграл - поменяй стратегию" также называется стратегией Павлова.
Начинает с сотрудничества. Если предыдущий раунд (Сотрудничество, Сотрудничество) либо (Предательство, Предательство), то есть стратегии совпали, то Сотрудничать в данном ходе. Иначе - Предательство.
import axelrod as axl
players = (axl.WinStayLoseShift(), axl.TitForTat())
match = axl.Match(players, turns=50)
match.play()
print(match.sparklines())██████████████████████████████████████████████████
██████████████████████████████████████████████████Этот код выведет список всех имеющихся в библиотеке axelrod стратегий (на момент публикации статьи - 239) с описанием на английском.
import axelrod as axl
print('Всего стратегий:', len(axl.strategies))
for strategy in axl.strategies:
print(strategy)
print(strategy.__doc__)
print('-' * 80)