В 1993 году на демопати Assembly, которая проходит в Финляндии, команда Future Crew презентовала свою новую работу «Second Reality».

(хороший разбор исходников этой демо можно найти здесь же на Хабре, по этой ссылке «Анализ кода демо Second Reality»)

Графические эффекты использованные в демо, в то время производили неизгладимое впечатление. Да и сегодня эту работу можно пересматривать с большим удовольствием. Под DosBox она запускается без каких-либо проблем. Именно это демо многие кодеры называли в качестве источника вдохновения для своих работ и толчком для них самих, чтобы начать заниматься компьютерной графикой.

Сегодня мы попробуем воспроизвести один из эффектов демонстрируемых в этом демо, а именно эффект плавающего туннеля.

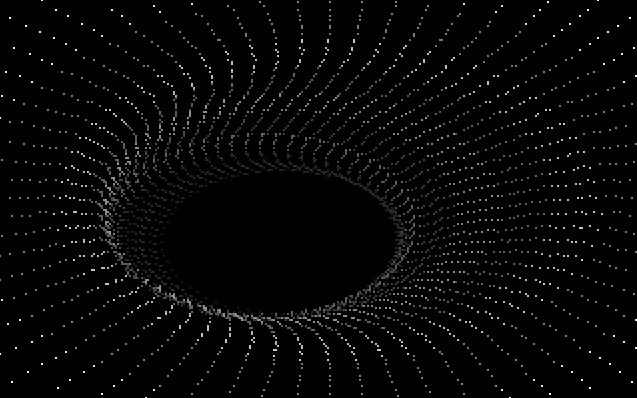
На экране мы видим набор эллипсов состоящих из отдельных точек. Эллипсы,  постепенно увеличиваясь, двигаются на нас. Дальние точки выглядят более тусклыми, чем точки на переднем плане. Общая анимация создает иллюзию движения сквозь извивающийся в пространстве туннель.

По способу экранного отображения точек, можно увидеть много общего с предыдущей частью (ссылка на 1 часть). Основное отличие, что здесь используются не случайно распределенные точки, а собранные в виде фигуры.

Поскольку нам нужно нарисовать множество эллипсов, значит нужно сразу где-то запомнить их количество, и нужен какой-то список Circles, чтобы хранить характеристики всех эллипсов. Запомним их количество в константе COUNT_CIRCLE, и пусть их будет 100.

Какие характеристики могут быть у одного эллипса: это X,Y координата центра, радиус и цвет. Т.е. четыре числовых значения. Радиус эллипса будет заменять нам такую характеристику как глубину, или ось Z, как вы заметили, я ее здесь не использую. Чем дальше от нас эллипс, тем его размер будет меньше.

В списке Circles будет храниться список из маленьких списков, это характеристики одного эллипса. Еще раз повторюсь, это будут: X, Y, Радиус, Цвет.

Первоначально все эллипсы располагаем в центре экрана.

Если посмотреть исходную демку внимательней, то видно, что на максимальном расстоянии вглубь туннеля, он не схлопывается в точку. Т.е. размер самого дальнего эллипса не нулевой.

Поэтому сделаем генерацию нового эллипса с диаметром отличным от 0, например 100. Эту величину можно крутить как угодно, кому как больше понравится.

Цвет в самой глубине туннеля, также не совершенно черный, поэтому начальное значение цвета сделаю равным 50, на свое усмотрение.

Теперь немного математики: как на экране нарисовать эллипс? В библиотеке pygame есть функция, которая умеет рисовать окружности и эллипсы. Но с ее помощью мы не нарисуем эллипс состоящий из точек. Поэтому делать это придется самим.

На помощь нам в данном случае придут тригонометрические функции синуса и косинуса. Их сочетание вместе и позволяет создать окружность, а затем и эллипс.

Если сильно упростить, то будет следующая формула для точки окружности:

где аlpha - угол на который отстоит точка на окружности.

т.е. чтобы полностью нарисовать окружность, нам нужно пройти по всей ее длине, а это, если вспомните геометрию:

Но нам не нужно вычислять ее длину, а нужно только менять угол для точки, полный круг по окружности это 360 градусов, или

Чтобы получить из окружности эллипс, сплюснутый по высоте, достаточно поделить итоговое значение по Y на какой-либо коэффициент, например на 1.5.

Еще раз повторим, как сформировать эллипс из точек: в цикле от 0 до 360 вычисляем координаты точек, из которых окружность состоит. Это координаты s_x и s_y.

s_y мы еще делим на 1.5, это для того, чтобы у нас получился эллипс сплюснутый по высоте.

Пусть точек в каждом эллипсе будет 100 штук, тогда шаг приращения для угла вычисляем как:

Естественно в функции отрисовки эллипса нужно не отображать точки, которые по координатам не входят в экран.

Чтобы конец нашего туннеля извивался “по змеиному”, воспользуемся также функциями синуса и косинуса. Заставим центр генерируемых эллипсов идти по окружности. Угол на который будет смещаться на каждом шаге наш туннель запомним в переменной rot, ее нужно описать до игрового цикла,  пусть он будет равным 0.05.

Чтобы равномерно распределить цвет эллипсов по туннелю, можно вычислить и запомнить в константе значение приращения цвета:

Здесь число 50 – это начальное значение цвета, чтобы самые дальние от нас эллипсы не были совершенно черными.

Приращение в радиусах эллипсов также запомним в константе STEP_RADIUS, и пусть оно будет равно 10.

Теперь самая интересная часть алгоритма - как сделать иллюзию движения по туннелю?

В цикле из списка берем один эллипс. Увеличиваем у него значение радиуса и яркости с помощью коэффициентов вычисленных ранее. Этот эллипс возвращаем в список не на свое место, а на порядковое место N+1, где N это индекс нашего эллипса в списке, т.е. его порядковый номер.

Таким образом, каждый эллипс перемещается за один проход игрового цикла, на одну ячейку вперед по списку, при этом координата его центра остается прежней, но увеличивается размер и становится ярче цвет. Благодаря этому и появляется эффект виляющего своим хвостом туннеля.

Маленькое замечание - удобнее по списку идти с конца, с окружности N-1 и двигаться к началу списка. Т.е, цикл в обратном направлении, в этом случае вычислений меньше.  И мы автоматически перезаписываем последнюю окружность в списке.

За один игровой цикл каждый из эллипсов увеличивает свой размер и цвет, а также перемещается в очереди «к выходу», т.е. к удалению из списка. Как только он вышел, то его место занимает новый эллипс, с параметрами по умолчанию, в начале списка.

Давайте посмотрим на полученный код:

import pygame
import math

SX = 800
SY = 800

pygame.init()
screen = pygame.display.set_mode((SX, SY))
running = True

COUNT_CIRCLE = 100                      # Всего эллипсов.
STEP_RADIUS = 10                        # Шаг увеличения радиуса.
STEP_COLOR = (255-50) / COUNT_CIRCLE    # Шаг увеличения цвета.

Circles = []    # Список содержащий эллипсы, каждый из них
                # является списком с: X, Y, RADIUS, COLOR

X = 0       # Номер координаты X в списке единичного эллипса.
Y = 1       # Номер координаты Y в списке единичного эллипса.
RADIUS = 2  # Номер радиуса в списке единичного эллипса.
COLOR = 3   # Номер цвета в списке единичного эллипса.

rot = 0.05  # Угол смещения центра туннеля.

# ---------------------------------------------------------------------------------------------
# Отрисовка одного эллипса на экране.
# На вход поступает эллипс circle из списка Circles.
# ---------------------------------------------------------------------------------------------
def draw_circle(circle):
    alpha = 0                   # Угол перемещения по эллипсу, для отрисовки точки.
    step = math.pi * 2 / 100    # Шаг, с которым рисуются точки эллипса.
    while alpha < math.pi * 2:
        s_x = round(circle[X] + math.sin(alpha) * circle[RADIUS])
        s_y = round(circle[Y] + math.cos(alpha) * circle[RADIUS] / 1.5)
        color = round(circle[COLOR])
        if 0 < s_x < SX and 0 < s_y < SY:
            pygame.draw.circle(screen, (color, color, color), (s_x, s_y), 2)
        alpha += step

# ---------------------------------------------------------------------------------------------
for i in range(0, COUNT_CIRCLE):
    Circles.append([SX // 2, SY // 2, 100, 50])       # Заполняем список с эллипсами, инициализируя их

while running:
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            running = False

    screen.fill((0, 0, 0))

    for i in range(len(Circles) - 2, -1, -1):
        c = Circles[i]
        c[RADIUS] += STEP_RADIUS
        c[COLOR] += STEP_COLOR
        Circles[i + 1] = c

        draw_circle(c)

    sx = SX // 2 + math.sin(rot) * 50.0        # Вычисление координаты X,Y для нового эллипса
    sy = SY // 2 + math.sin(rot) * 50.0

    Circles[0] = [sx, sy, 100, 50]
    rot += 0.05

    pygame.display.flip()

pygame.quit()

Получим примерно такую картинку:

В следующей части будем реализовывать довольно старый алгоритм, имитирующий изображение пламени.

Ссылка на 1 часть - алгоритм "Starfield Simulation"