https://habr.com/ru/company/ruvds/blog/488342/

• Блог компании RUVDS.com
• Python
• Алгоритмы

У специалистов по обработке и анализу данных есть множество средств для создания классификационных моделей. Один из самых популярных и надёжных методов разработки таких моделей заключается в использовании алгоритма «случайный лес» (Random Forest, RF). Для того чтобы попытаться улучшить показатели модели, построенной с использованием алгоритма RF, можно воспользоваться оптимизацией гиперпараметров модели (Hyperparameter Tuning, HT).



Кроме того, распространён подход, в соответствии с которым данные, перед их передачей в модель, обрабатывают с помощью метода главных компонент (Principal Component Analysis, PCA). Но стоит ли вообще этим пользоваться? Разве основная цель алгоритма RF заключается не в том, чтобы помочь аналитику интерпретировать важность признаков?

Да, применение алгоритма PCA может привести к небольшому усложнению интерпретации каждого «признака» при анализе «важности признаков» RF-модели. Однако алгоритм PCA производит уменьшение размерности пространства признаков, что может привести к уменьшению количества признаков, которые нужно обработать RF-моделью. Обратите внимание на то, что объёмность вычислений — это один из основных минусов алгоритма «случайный лес» (то есть — выполнение модели может занять немало времени). Применение алгоритма PCA может стать весьма важной частью моделирования, особенно в тех случаях, когда работают с сотнями или даже с тысячами признаков. В результате, если самое важное — это просто создать наиболее эффективную модель, и при этом можно пожертвовать точностью определения важности признаков, тогда PCA, вполне возможно, стоит попробовать.

Теперь — к делу. Мы будем работать с набором данных по раку груди — Scikit-learn «breast cancer». Мы создадим три модели и сравним их эффективность. А именно, речь идёт о следующих моделях:

1. Базовая модель, основанная на алгоритме RF (будем сокращённо называть эту модель RF).
2. Та же модель, что и №1, но такая, в которой применяется уменьшение размерности пространства признаков с помощью метода главных компонент (RF + PCA).
3. Такая же модель, как и №2, но построенная с применением оптимизации гиперпараметров (RF + PCA + HT).

1. Импорт данных

Для начала загрузим данные и создадим датафрейм Pandas. Так как мы пользуемся предварительно очищенным «игрушечным» набором данных из Scikit-learn, то после этого мы уже сможем приступить к процессу моделирования. Но даже при использовании подобных данных рекомендуется всегда начинать работу, проведя предварительный анализ данных с использованием следующих команд, применяемых к датафрейму (df):

• df.head() — чтобы взглянуть на новый датафрейм и понять, выглядит ли он так, как ожидается.
• df.info() — чтобы выяснить особенности типов данных и содержимого столбцов. Возможно, перед продолжением работы понадобится произвести преобразование типов данных.
• df.isna() — чтобы убедиться в том, что в данных нет значений NaN. Соответствующие значения, если они есть, может понадобиться как-то обработать, или, если нужно, может понадобиться убрать целые строки из датафрейма.
• df.describe() — чтобы выяснить минимальные, максимальные, средние значения показателей в столбцах, чтобы узнать показатели среднеквадратического и вероятного отклонения по столбцам.

В нашем наборе данных столбец cancer (рак) — это целевая переменная, значение которой мы хотим предсказать, используя модель. 0 означает «отсутствие заболевания». 1 — «наличие заболевания».

import pandas as pd
from sklearn.datasets import load_breast_cancer
columns = ['mean radius', 'mean texture', 'mean perimeter', 'mean area', 'mean smoothness', 'mean compactness', 'mean concavity', 'mean concave points', 'mean symmetry', 'mean fractal dimension', 'radius error', 'texture error', 'perimeter error', 'area error', 'smoothness error', 'compactness error', 'concavity error', 'concave points error', 'symmetry error', 'fractal dimension error', 'worst radius', 'worst texture', 'worst perimeter', 'worst area', 'worst smoothness', 'worst compactness', 'worst concavity', 'worst concave points', 'worst symmetry', 'worst fractal dimension']
dataset = load_breast_cancer()
data = pd.DataFrame(dataset['data'], columns=columns)
data['cancer'] = dataset['target']
display(data.head())
display(data.info())
display(data.isna().sum())
display(data.describe())

Фрагмент датафрейма с данными по раку груди. Каждая строка содержит результаты наблюдений за пациентом. Последний столбец, cancer, содержит целевую переменную, которую мы пытаемся предсказать. 0 означает «отсутствие заболевания». 1 — «наличие заболевания»

2. Разделение набора данных на учебные и проверочные данные

Теперь разделим данные с использованием функции Scikit-learn train_test_split. Мы хотим дать модели как можно больше учебных данных. Однако нужно, чтобы в нашем распоряжении было бы достаточно данных для проверки модели. В целом можно сказать, что, по мере роста количества строк в наборе данных, растёт и объём данных, которые можно рассматривать в качестве учебных.

Например, если есть миллионы строк, можно разделить набор, выделив 90% строк на учебные данные и 10% — на проверочные. Но исследуемый набор данных содержит лишь 569 строк. А это — не так уж и много для тренировки и проверки модели. В результате для того, чтобы быть справедливыми по отношению к учебным и проверочным данным, мы разделим набор на две равные части — 50% — учебные данные и 50% — проверочные. Мы устанавливаем stratify=y для обеспечения того, чтобы и в учебном, и в проверочном наборах данных присутствовало бы то же соотношение 0 и 1, что и в исходном наборе данных.

from sklearn.model_selection import train_test_split
X = data.drop('cancer', axis=1)  
y = data['cancer'] 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.50, random_state = 2020, stratify=y)

3. Масштабирование данных

Прежде чем приступать к моделированию, нужно выполнить «центровку» и «стандартизацию» данных путём их масштабирования. Масштабирование выполняется из-за того, что разные величины выражены в разных единицах измерения. Эта процедура позволяет организовать «честную схватку» между признаками при определении их важности. Кроме того, мы конвертируем y_train из типа данных Pandas Series в массив NumPy для того чтобы позже модель смогла бы работать с соответствующими целевыми показателями.

import numpy as np
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
X_train_scaled = ss.fit_transform(X_train)
X_test_scaled = ss.transform(X_test)
y_train = np.array(y_train)

4. Обучение базовой модели (модель №1, RF)

Сейчас создадим модель №1. В ней, напомним, применяется только алгоритм Random Forest. Она использует все признаки и настроена с использованием значений, задаваемых по умолчанию (подробности об этих настройках можно найти в документации к sklearn.ensemble.RandomForestClassifier). Сначала инициализируем модель. После этого обучим её на масштабированных данных. Точность модели можно измерить на учебных данных:

from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import recall_score
rfc = RandomForestClassifier()
rfc.fit(X_train_scaled, y_train)
display(rfc.score(X_train_scaled, y_train))
# 1.0

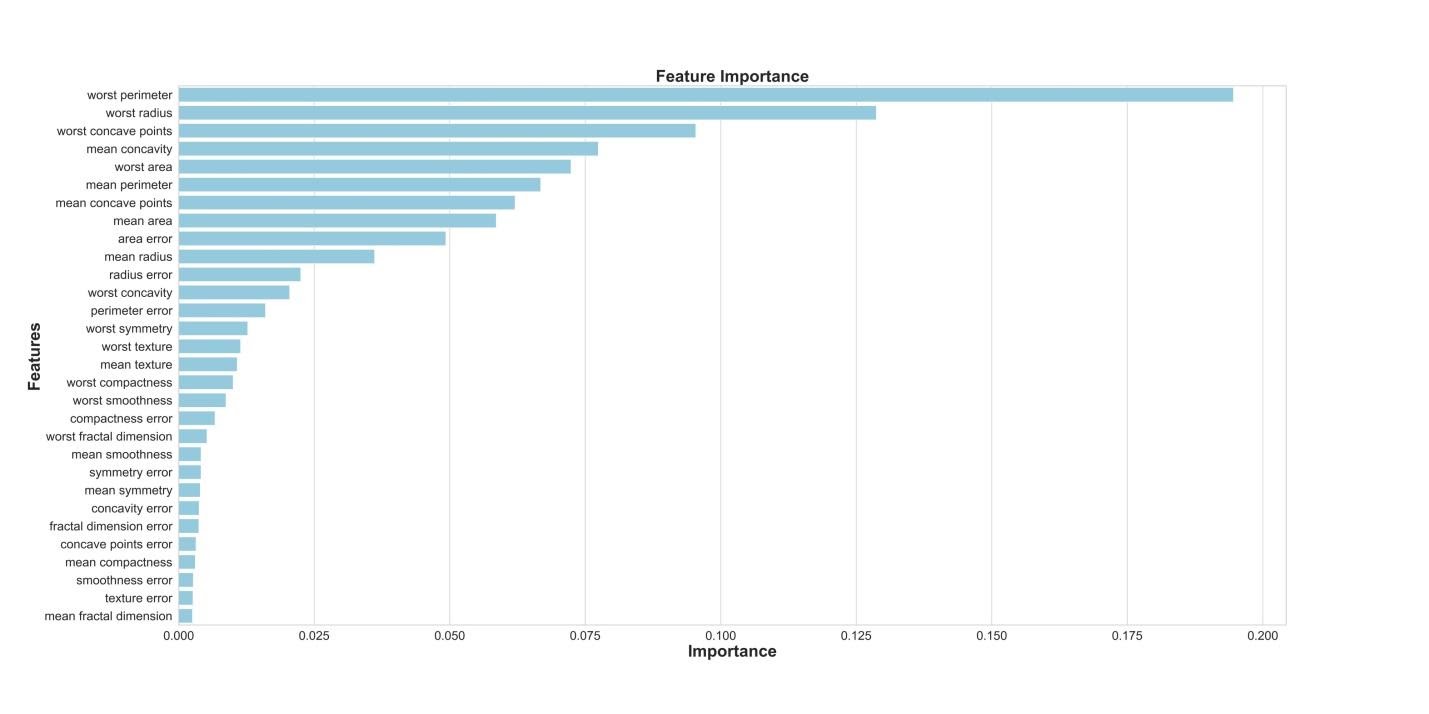
Если нам интересно узнать о том, какие признаки являются самыми важными для RF-модели в деле предсказания рака груди, мы можем визуализировать и квантифицировать показатели важности признаков, обратившись к атрибуту feature_importances_:

feats = {}
for feature, importance in zip(data.columns, rfc_1.feature_importances_):
    feats[feature] = importance
importances = pd.DataFrame.from_dict(feats, orient='index').rename(columns={0: 'Gini-Importance'})
importances = importances.sort_values(by='Gini-Importance', ascending=False)
importances = importances.reset_index()
importances = importances.rename(columns={'index': 'Features'})
sns.set(font_scale = 5)
sns.set(style="whitegrid", color_codes=True, font_scale = 1.7)
fig, ax = plt.subplots()
fig.set_size_inches(30,15)
sns.barplot(x=importances['Gini-Importance'], y=importances['Features'], data=importances, color='skyblue')
plt.xlabel('Importance', fontsize=25, weight = 'bold')
plt.ylabel('Features', fontsize=25, weight = 'bold')
plt.title('Feature Importance', fontsize=25, weight = 'bold')
display(plt.show())
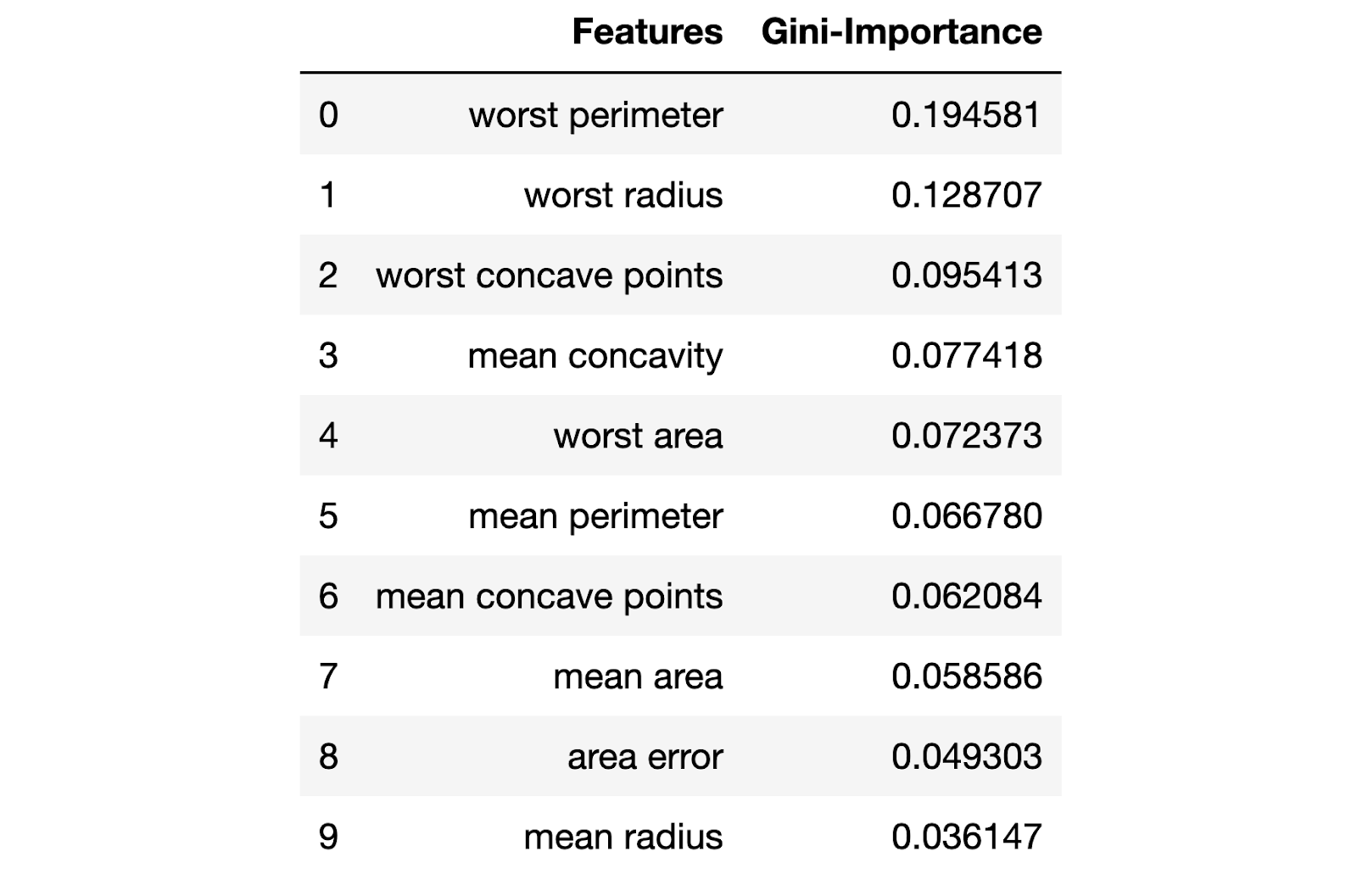
display(importances)

Визуализация «важности» признаков


Показатели важности признаков

5. Метод главных компонент

Теперь зададимся вопросом о том, как можно улучшить базовую RF-модель. С использованием методики снижения размерности пространства признаков можно представить исходный набор данных через меньшее количество переменных и при этом снизить объём вычислительных ресурсов, необходимых для обеспечения работы модели. Используя PCA, можно изучить кумулятивную выборочную дисперсию этих признаков для того чтобы понять то, какие признаки объясняют большую часть дисперсии в данных.
Инициализируем объект PCA (pca_test), указывая количество компонент (признаков), которые нужно рассмотреть. Мы устанавливаем этот показатель в 30 для того чтобы увидеть объяснённую дисперсию всех сгенерированных компонент до того, как примем решение о том, сколько компонент нам понадобится. Затем передаём в pca_test масштабированные данные X_train, пользуясь методом pca_test.fit(). После этого визуализируем данные.

import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.decomposition import PCA
pca_test = PCA(n_components=30)
pca_test.fit(X_train_scaled)
sns.set(style='whitegrid')
plt.plot(np.cumsum(pca_test.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance')
plt.axvline(linewidth=4, color='r', linestyle = '--', x=10, ymin=0, ymax=1)
display(plt.show())
evr = pca_test.explained_variance_ratio_
cvr = np.cumsum(pca_test.explained_variance_ratio_)
pca_df = pd.DataFrame()
pca_df['Cumulative Variance Ratio'] = cvr
pca_df['Explained Variance Ratio'] = evr
display(pca_df.head(10))

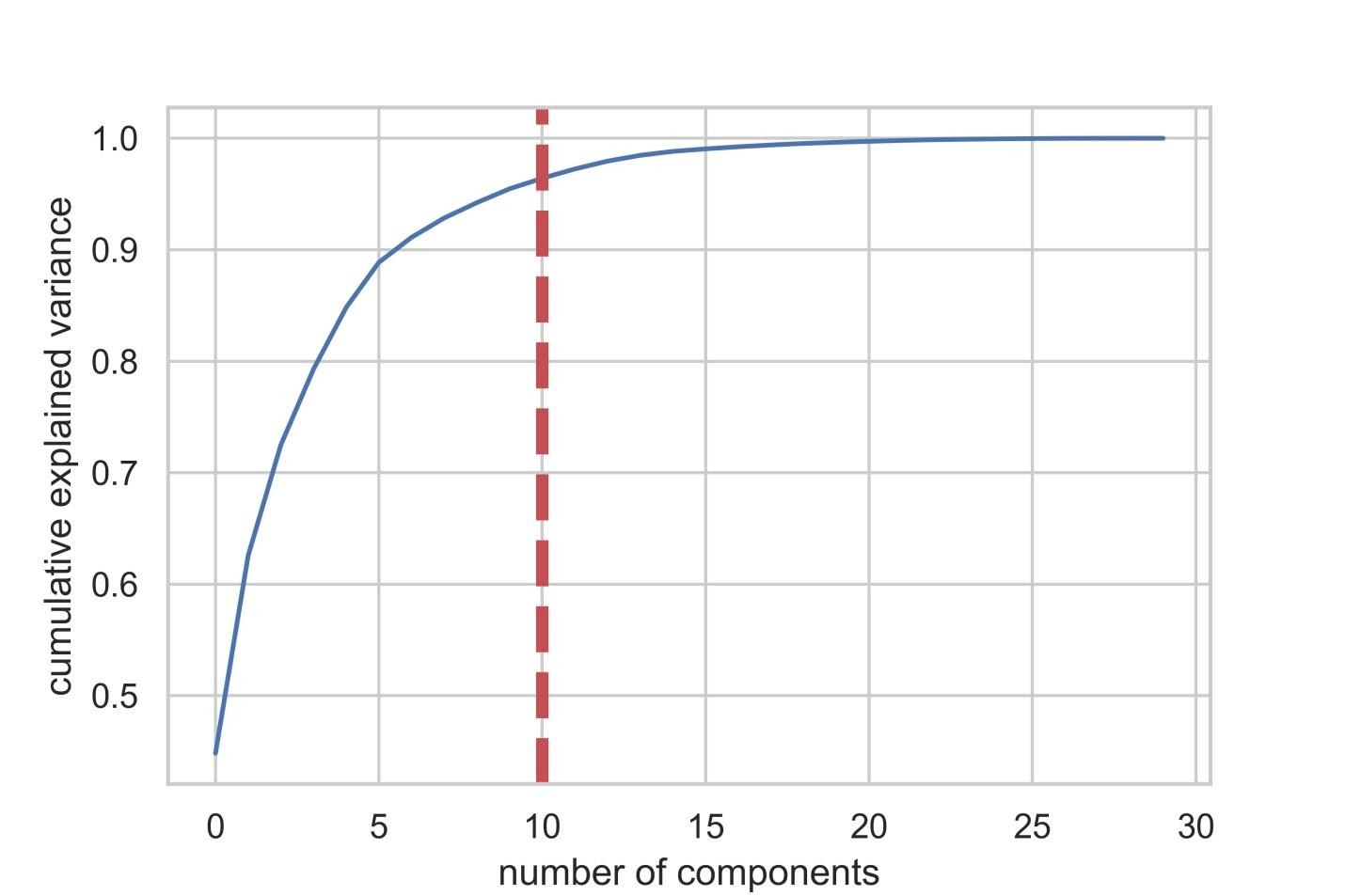
После того, как число используемых компонент превышает 10, рост их количества не очень сильно повышает объяснённую дисперсию


Этот датафрейм содержит такие показатели, как Cumulative Variance Ratio (кумулятивный размер объяснённой дисперсии данных) и Explained Variance Ratio (вклад каждой компоненты в общий объём объяснённой дисперсии)

Если взглянуть на вышеприведённый датафрейм, то окажется, что использование PCA для перехода от 30 переменных к 10 компонентам позволяет объяснить 95% дисперсии данных. Другие 20 компонент объясняют менее 5% дисперсии, а это значит, что от них мы можем отказаться. Следуя этой логике, воспользуемся PCA для уменьшения числа компонент с 30 до 10 для X_train и X_test. Запишем эти искусственно созданные наборы данных «пониженной размерности» в X_train_scaled_pca и в X_test_scaled_pca.

pca = PCA(n_components=10)
pca.fit(X_train_scaled)
X_train_scaled_pca = pca.transform(X_train_scaled)
X_test_scaled_pca = pca.transform(X_test_scaled)

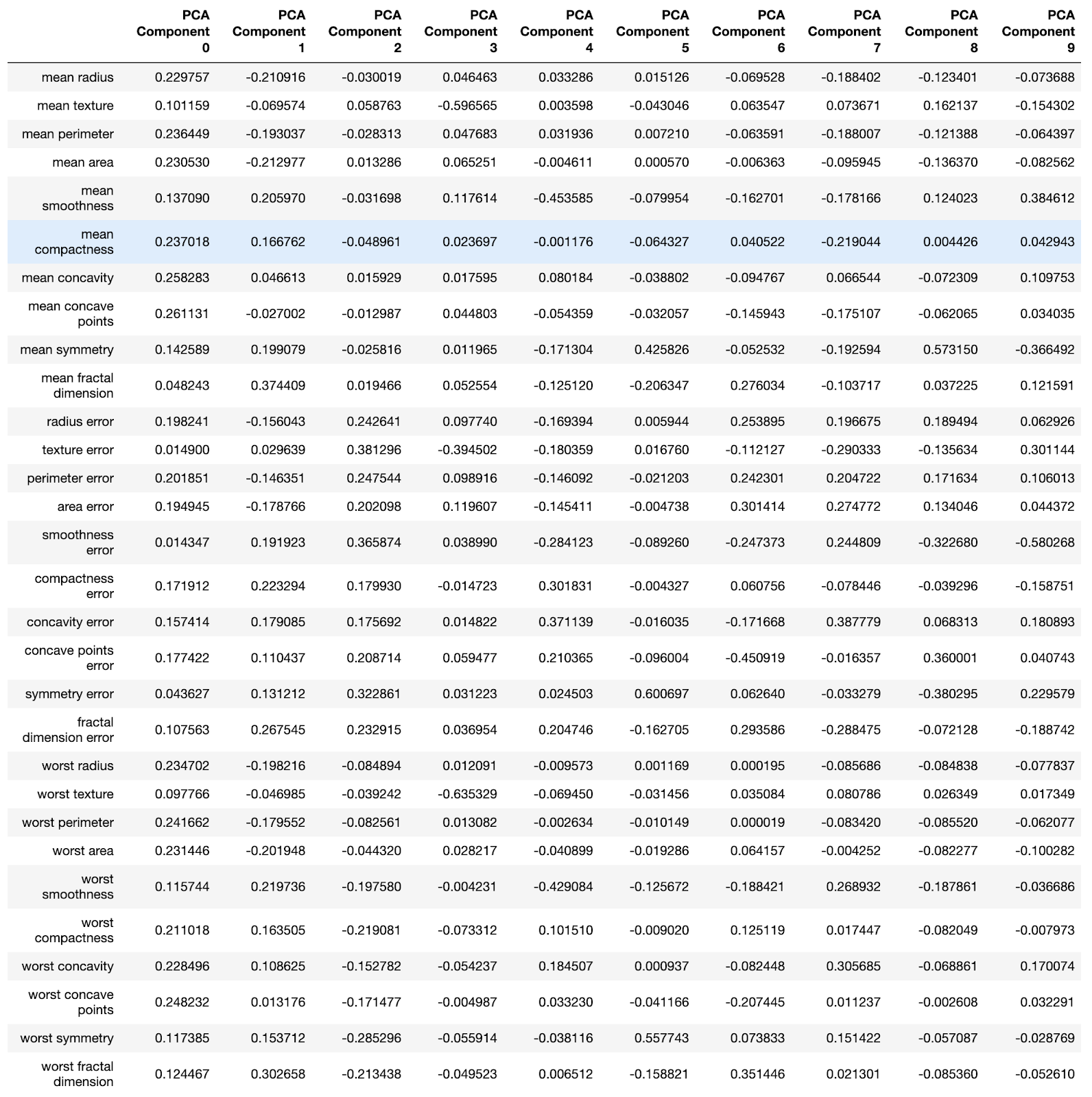
Каждая компонента — это линейная комбинация исходных переменных с соответствующими «весами». Мы можем видеть эти «веса» для каждой компоненты, создав датафрейм.

pca_dims = []
for x in range(0, len(pca_df)):
    pca_dims.append('PCA Component {}'.format(x))
pca_test_df = pd.DataFrame(pca_test.components_, columns=columns, index=pca_dims)
pca_test_df.head(10).T

Датафрейм со сведениями по компонентам

6. Обучение базовой RF-модели после применения к данным метода главных компонент (модель №2, RF + PCA)

Теперь мы можем передать в ещё одну базовую RF-модель данные X_train_scaled_pca и y_train и можем узнать о том, есть ли улучшения в точности предсказаний, выдаваемых моделью.

rfc = RandomForestClassifier()
rfc.fit(X_train_scaled_pca, y_train)
display(rfc.score(X_train_scaled_pca, y_train))
# 1.0

Модели сравним ниже.

7. Оптимизация гиперпараметров. Раунд 1: RandomizedSearchCV

После обработки данных с использованием метода главных компонент можно попытаться воспользоваться оптимизацией гиперпараметров модели для того чтобы улучшить качество предсказаний, выдаваемых RF-моделью. Гиперпараметры можно рассматривать как что-то вроде «настроек» модели. Настройки, которые отлично подходят для одного набора данных, для другого не подойдут — поэтому и нужно заниматься их оптимизацией.

Начать можно с алгоритма RandomizedSearchCV, который позволяет довольно грубо исследовать широкие диапазоны значений. Описания всех гиперпараметров для RF-моделей можно найти здесь.

В ходе работы мы генерируем сущность param_dist, содержащую, для каждого гиперпараметра, диапазон значений, которые нужно испытать. Далее, мы инициализируем объект rs с помощью функции RandomizedSearchCV(), передавая ей RF-модель, param_dist, число итераций и число кросс-валидаций, которые нужно выполнить.

Гиперпараметр verbose позволяет управлять объёмом информации, который выводится моделью в ходе её работы (наподобие вывода сведений в процессе обучения модели). Гиперпараметр n_jobs позволяет указывать то, сколько процессорных ядер нужно использовать для обеспечения работы модели. Установка n_jobs в значение -1 приведёт к более быстрой работе модели, так как при этом будут использоваться все ядра процессора.

Мы будем заниматься подбором следующих гиперпараметров:

• n_estimators — число «деревьев» в «случайном лесу».
• max_features — число признаков для выбора расщепления.
• max_depth — максимальная глубина деревьев.
• min_samples_split — минимальное число объектов, необходимое для того, чтобы узел дерева мог бы расщепиться.
• min_samples_leaf — минимальное число объектов в листьях.
• bootstrap — использование для построения деревьев подвыборки с возвращением.

from sklearn.model_selection import RandomizedSearchCV
n_estimators = [int(x) for x in np.linspace(start = 100, stop = 1000, num = 10)]
max_features = ['log2', 'sqrt']
max_depth = [int(x) for x in np.linspace(start = 1, stop = 15, num = 15)]
min_samples_split = [int(x) for x in np.linspace(start = 2, stop = 50, num = 10)]
min_samples_leaf = [int(x) for x in np.linspace(start = 2, stop = 50, num = 10)]
bootstrap = [True, False]
param_dist = {'n_estimators': n_estimators,
               'max_features': max_features,
               'max_depth': max_depth,
               'min_samples_split': min_samples_split,
               'min_samples_leaf': min_samples_leaf,
               'bootstrap': bootstrap}
rs = RandomizedSearchCV(rfc_2, 
                        param_dist, 
                        n_iter = 100, 
                        cv = 3, 
                        verbose = 1, 
                        n_jobs=-1, 
                        random_state=0)
rs.fit(X_train_scaled_pca, y_train)
rs.best_params_
# {'n_estimators': 700,
# 'min_samples_split': 2,
# 'min_samples_leaf': 2,
# 'max_features': 'log2',
# 'max_depth': 11,
# 'bootstrap': True}

При значениях параметров n_iter = 100 и cv = 3, мы создали 300 RF-моделей, случайно выбирая комбинации представленных выше гиперпараметров. Мы можем обратиться к атрибуту best_params_ для получения сведений о наборе параметров, позволяющем создать самую лучшую модель. Но на данной стадии это может не дать нам наиболее интересных данных о диапазонах параметров, которые стоит изучить на следующем раунде оптимизации. Для того чтобы выяснить то, в каком диапазоне значений стоит продолжать поиск, мы легко можем получить датафрейм, содержащий результаты работы алгоритма RandomizedSearchCV.

rs_df = pd.DataFrame(rs.cv_results_).sort_values('rank_test_score').reset_index(drop=True)
rs_df = rs_df.drop([
            'mean_fit_time', 
            'std_fit_time', 
            'mean_score_time',
            'std_score_time', 
            'params', 
            'split0_test_score', 
            'split1_test_score', 
            'split2_test_score', 
            'std_test_score'],
            axis=1)
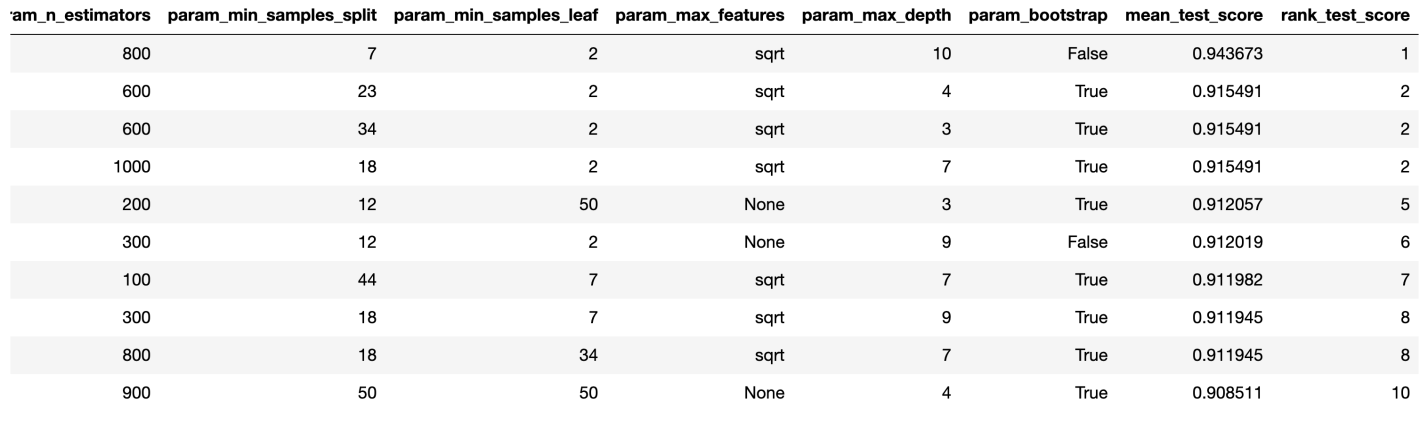
rs_df.head(10)

Результаты работы алгоритма RandomizedSearchCV

Теперь создадим столбчатые графики, на которых, по оси Х, расположены значения гиперпараметров, а по оси Y — средние значения, показываемые моделями. Это позволит понять то, какие значения гиперпараметров, в среднем, лучше всего себя показывают.

fig, axs = plt.subplots(ncols=3, nrows=2)
sns.set(style="whitegrid", color_codes=True, font_scale = 2)
fig.set_size_inches(30,25)
sns.barplot(x='param_n_estimators', y='mean_test_score', data=rs_df, ax=axs[0,0], color='lightgrey')
axs[0,0].set_ylim([.83,.93])axs[0,0].set_title(label = 'n_estimators', size=30, weight='bold')
sns.barplot(x='param_min_samples_split', y='mean_test_score', data=rs_df, ax=axs[0,1], color='coral')
axs[0,1].set_ylim([.85,.93])axs[0,1].set_title(label = 'min_samples_split', size=30, weight='bold')
sns.barplot(x='param_min_samples_leaf', y='mean_test_score', data=rs_df, ax=axs[0,2], color='lightgreen')
axs[0,2].set_ylim([.80,.93])axs[0,2].set_title(label = 'min_samples_leaf', size=30, weight='bold')
sns.barplot(x='param_max_features', y='mean_test_score', data=rs_df, ax=axs[1,0], color='wheat')
axs[1,0].set_ylim([.88,.92])axs[1,0].set_title(label = 'max_features', size=30, weight='bold')
sns.barplot(x='param_max_depth', y='mean_test_score', data=rs_df, ax=axs[1,1], color='lightpink')
axs[1,1].set_ylim([.80,.93])axs[1,1].set_title(label = 'max_depth', size=30, weight='bold')
sns.barplot(x='param_bootstrap',y='mean_test_score', data=rs_df, ax=axs[1,2], color='skyblue')
axs[1,2].set_ylim([.88,.92])
axs[1,2].set_title(label = 'bootstrap', size=30, weight='bold')
plt.show()

Анализ значений гиперпараметров

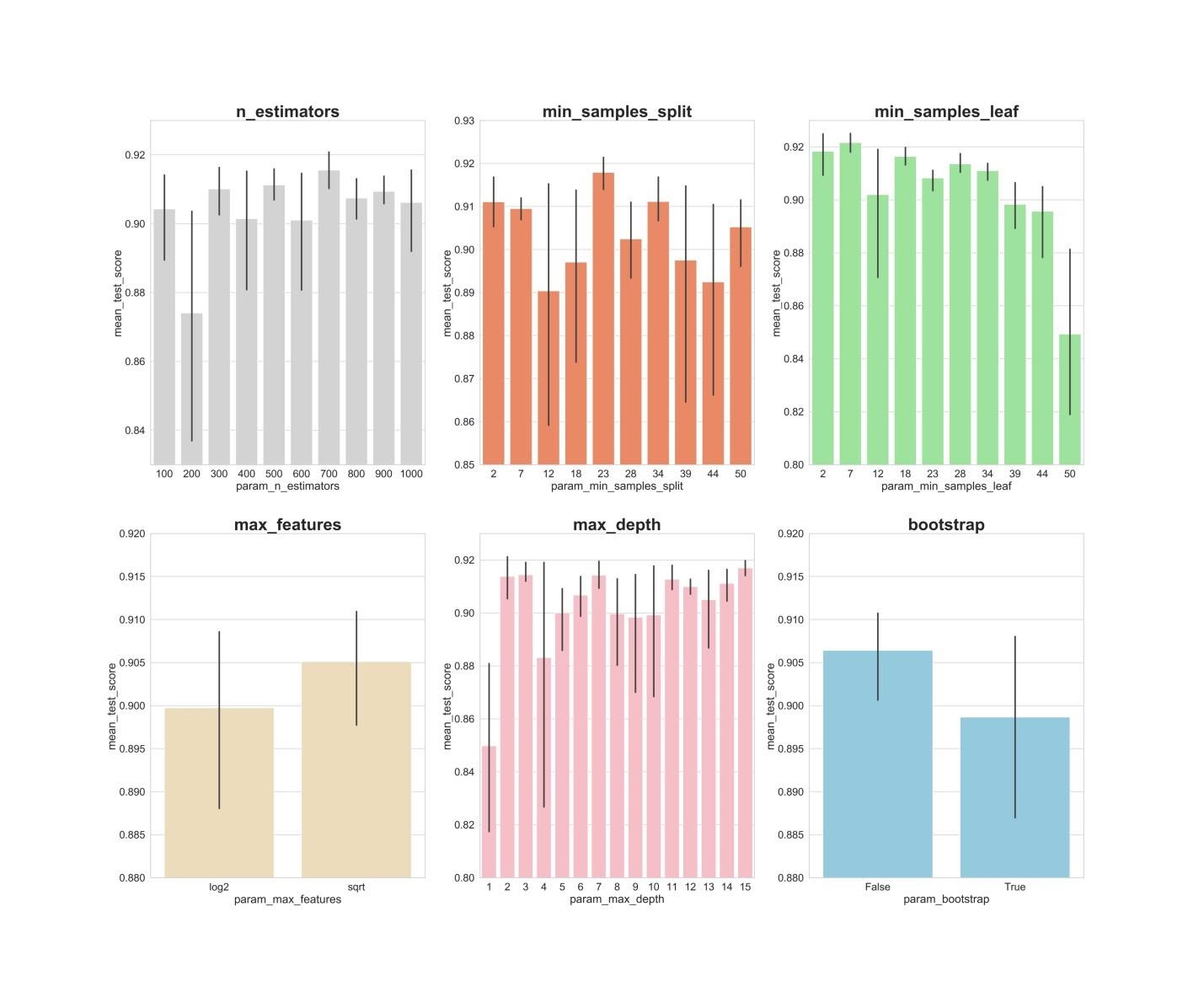
Если проанализировать вышеприведённые графики, то можно заметить некоторые интересные вещи, говорящие о том, как, в среднем, каждое значение гиперпараметра влияет на модель.

• n_estimators: значения 300, 500, 700, видимо, показывают наилучшие средние результаты.
• min_samples_split: маленькие значения, вроде 2 и 7, как кажется, показывают наилучшие результаты. Хорошо выглядит и значение 23. Можно исследовать несколько значений этого гиперпараметра, превышающих 2, а также — несколько значений около 23.
• min_samples_leaf: возникает такое ощущение, что маленькие значения этого гиперпараметра дают более высокие результаты. А это значит, что мы можем испытать значения между 2 и 7.
• max_features: вариант sqrt даёт самый высокий средний результат.
• max_depth: тут чёткой зависимости между значением гиперпараметра и результатом работы модели не видно, но есть ощущение, что значения 2, 3, 7, 11, 15 выглядят неплохо.
• bootstrap: значение False показывает наилучший средний результат.

Теперь мы, воспользовавшись этими находками, можем перейти ко второму раунду оптимизации гиперпараметров. Это позволит сузить спектр интересующих нас значений.

8. Оптимизация гиперпараметров. Раунд 2: GridSearchCV (окончательная подготовка параметров для модели №3, RF + PCA + HT)

После применения алгоритма RandomizedSearchCV воспользуемся алгоритмом GridSearchCV для проведения более точного поиска наилучшей комбинации гиперпараметров. Здесь исследуются те же гиперпараметры, но теперь мы применяем более «обстоятельный» поиск их наилучшей комбинации. При использовании алгоритма GridSearchCV исследуется каждая комбинация гиперпараметров. Это требует гораздо больших вычислительных ресурсов, чем использование алгоритма RandomizedSearchCV, когда мы самостоятельно задаём число итераций поиска. Например, исследование 10 значений для каждого из 6 гиперпараметров с кросс-валидацией по 3 блокам потребует 10⁶ x 3, или 3000000 сеансов обучения модели. Именно поэтому мы и используем алгоритм GridSearchCV после того, как, применив RandomizedSearchCV, сузили диапазоны значений исследуемых параметров.

Итак, используя то, что мы выяснили с помощью RandomizedSearchCV, исследуем значения гиперпараметров, которые лучше всего себя показали:

from sklearn.model_selection import GridSearchCV
n_estimators = [300,500,700]
max_features = ['sqrt']
max_depth = [2,3,7,11,15]
min_samples_split = [2,3,4,22,23,24]
min_samples_leaf = [2,3,4,5,6,7]
bootstrap = [False]
param_grid = {'n_estimators': n_estimators,
               'max_features': max_features,
               'max_depth': max_depth,
               'min_samples_split': min_samples_split,
               'min_samples_leaf': min_samples_leaf,
               'bootstrap': bootstrap}
gs = GridSearchCV(rfc_2, param_grid, cv = 3, verbose = 1, n_jobs=-1)
gs.fit(X_train_scaled_pca, y_train)
rfc_3 = gs.best_estimator_
gs.best_params_
# {'bootstrap': False,
# 'max_depth': 7,
# 'max_features': 'sqrt',
# 'min_samples_leaf': 3,
# 'min_samples_split': 2,
# 'n_estimators': 500}

Здесь мы применяем кросс-валидацию по 3 блокам для 540 (3 x 1 x 5 x 6 x 6 x 1) сеансов обучения модели, что даёт 1620 сеансов обучения модели. И уже теперь, после того, как мы воспользовались RandomizedSearchCV и GridSearchCV, мы можем обратиться к атрибуту best_params_ для того чтобы узнать о том, какие значения гиперпараметров позволяют модели наилучшим образом работать с исследуемым набором данных (эти значения можно видеть в нижней части предыдущего блока кода). Эти параметры используются при создании модели №3.

9. Оценка качества работы моделей на проверочных данных

Теперь можно оценить созданные модели на проверочных данных. А именно, речь идёт о тех трёх моделях, описанных в самом начале материала.

Проверим эти модели:

y_pred = rfc.predict(X_test_scaled)
y_pred_pca = rfc.predict(X_test_scaled_pca)
y_pred_gs = gs.best_estimator_.predict(X_test_scaled_pca)

Создадим матрицы ошибок для моделей и узнаем о том, как хорошо каждая из них способна предсказывать рак груди:

from sklearn.metrics import confusion_matrix
conf_matrix_baseline = pd.DataFrame(confusion_matrix(y_test, y_pred), index = ['actual 0', 'actual 1'], columns = ['predicted 0', 'predicted 1'])
conf_matrix_baseline_pca = pd.DataFrame(confusion_matrix(y_test, y_pred_pca), index = ['actual 0', 'actual 1'], columns = ['predicted 0', 'predicted 1'])
conf_matrix_tuned_pca = pd.DataFrame(confusion_matrix(y_test, y_pred_gs), index = ['actual 0', 'actual 1'], columns = ['predicted 0', 'predicted 1'])
display(conf_matrix_baseline)
display('Baseline Random Forest recall score', recall_score(y_test, y_pred))
display(conf_matrix_baseline_pca)
display('Baseline Random Forest With PCA recall score', recall_score(y_test, y_pred_pca))
display(conf_matrix_tuned_pca)
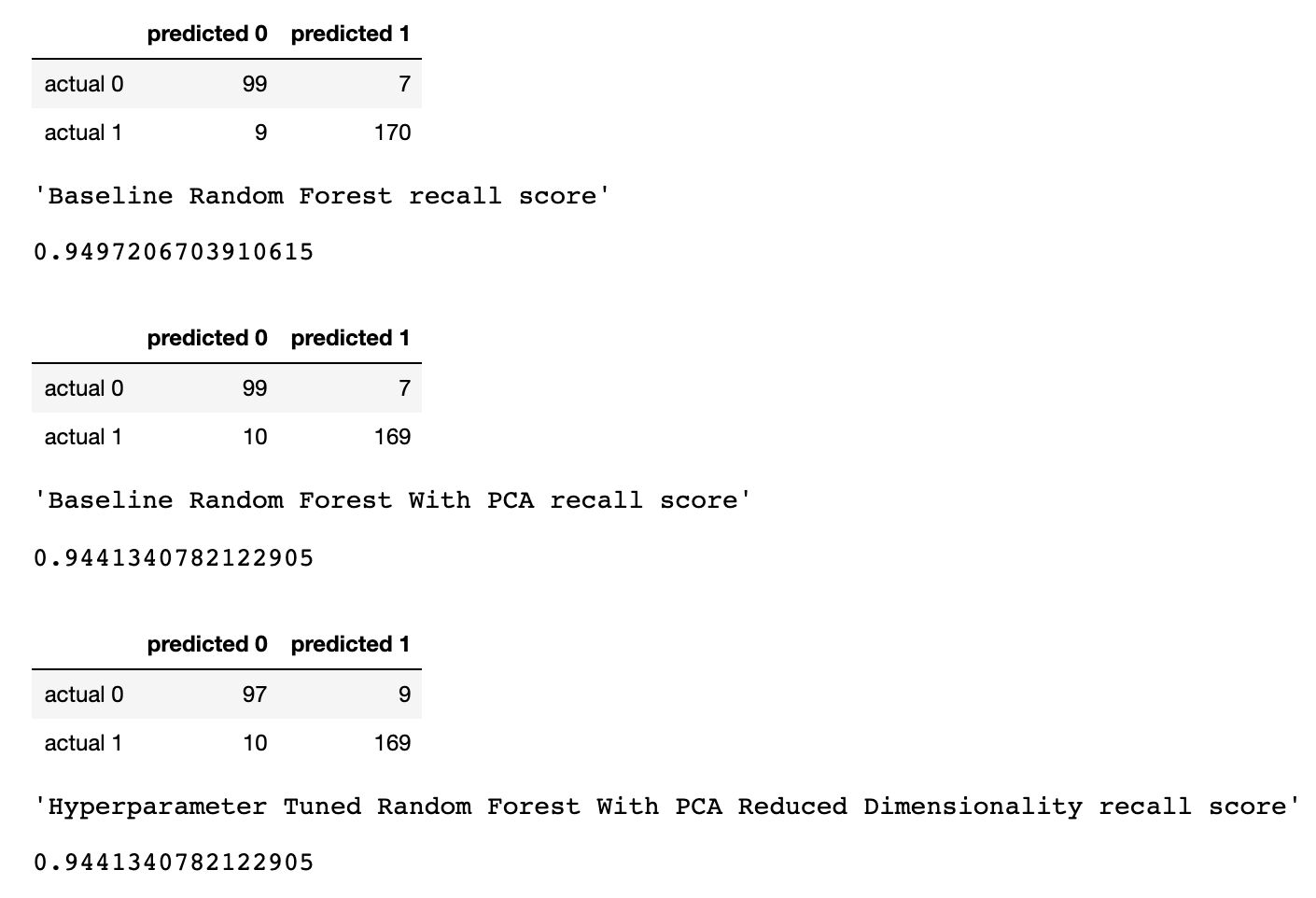
display('Hyperparameter Tuned Random Forest With PCA Reduced Dimensionality recall score', recall_score(y_test, y_pred_gs))

Результаты работы трёх моделей

Здесь оценивается метрика «полнота» (recall). Дело в том, что мы имеем дело с диагнозом рака. Поэтому нас чрезвычайно интересует минимизация ложноотрицательных прогнозов, выдаваемых моделями.

Учитывая это, можно сделать вывод о том, что базовая RF-модель дала наилучшие результаты. Её показатель полноты составил 94.97%. В проверочном наборе данных была запись о 179 пациентах, у которых есть рак. Модель нашла 170 из них.

Итоги

Это исследование позволяет сделать важное наблюдение. Иногда RF-модель, в которой используется метод главных компонент и широкомасштабная оптимизация гиперпараметров, может работать не так хорошо, как самая обыкновенная модель со стандартными настройками. Но это — не повод для того, чтобы ограничивать себя лишь простейшими моделями. Не попробовав разные модели, нельзя сказать о том, какая из них покажет наилучший результат. А в случае с моделями, которые используются для предсказания наличия у пациентов рака, можно сказать, что чем лучше модель — тем больше жизней может быть спасено.

Уважаемые читатели! Какие задачи вы решаете, привлекая методы машинного обучения?