• Машинное обучение
• Математика
• Python
• Data Mining
• Блог компании Open Data Science

PyMC3 — МСМС и не только

Привет, Хабрахабр!

В этом посте уже упоминался PyMC3. Там можно почитать про основы MCMC-сэмплирования. Здесь я расскажу про вариационный вывод (ADVI), про то, зачем все это нужно и покажу на довольно простых примерах из галереи PyMC3, чем это может быть полезно. Одним из таких примеров будет байесовская нейронная сеть для задачи классификации, но это в самом конце. Кому интересно — добро пожаловать!

Введение

Прежде чем переходить к основной части, считаю необходимым освежить терминологию байесовского анализа. Предмет этого подраздела теории вероятностей — вывод апостериорного распределения. Задача выглядит следующим образом:

Аналитик хочет что-то узнать о ненаблюдаемых (латентных) параметрах модели $$ и у него есть некие соображения на счет того, какими они могут быть $$. Кроме того, он может судить о том, как хорошо его данные $$ ложатся в модель с параметрами $$. Выражается это через правдоподобие $$ — вероятность наблюдать данные при заданных параметрах.

Где

• $$ — априорное распределение, предположения насчет предполагаемых результатов.
  Когда подходишь к решению задачи, очень часто есть представление о том явлении, которое исследуется.

  
  
  • Например, возьмем область физики. Там есть законы и механизмы взаимодействия, о них мы имеем хорошее представление (за исключением некоторых величин, как, например, коэффициент трения какого-то вещества с поверхностью). Мы примерно предполагаем, каким он должен быть, исходя из прошлого опыта и накопленных знаний. Хотя бы то, что он больше нуля. Мы можем построить эксперимент, составив физическую модель с неизвестным параметром, который хочется оценить.
  • Важное замечание: Иногда возникает соблазн подстраивать априорное распределение под наблюдаемые данные. Скажем, например, что мы прикинули на даннных, что искомый $$ где-то около $$ и начинаем выводить апостериорное. Постойте, но когда вы, например, доказываете теорему, вы же не пользуетесь ее результатами для ее же доказательства? Так же и здесь, априорное распределение не должно опираться на изучаемый набор данных.
  
  
• $$ — правдоподобие, оценка адекватности предполагаемого $$. Выражается в вероятности наблюдать данные при условии выбранной гипотезы на $$.
  
  • У нас есть результаты эксперимента, для каждого набора параметров мы можем оценивать, "насколько хорошо модель описывает мир". Эту идею используют классические статистики при MLE оценке.
• $$ — апостериорное распределение, выводы, которые мы хотим получить.
  
  • По сути это те представления о неизвестных параметрах модели (коэф. трения), которые сложились у нас в ходе проведения эксперимента. Можно считать это компромиссом между старыми знаниями и новыми, выраженными через $$ и $$ соответственно.
• $$ — Evidence, вероятность получить такие данные вообще, на русский переводится скверно.

Байесовский вывод

На первый взгляд, ничего особенного: у нас есть формулы плотностей $$, $$, искомая плотность выглядит следующим образом:

Перемножить две плотности — не проблема. Посчитать интеграл снизу?.. Хм, ну можно вспомнить университетский курс матанализа… В общем берем, подставляем все в формулу и готово. Вооружившись этим знанием, можно смело отправляться исследовать простые модели с простыми распределениями. Однако в более менее приближенных к жизни примерах, даже такое знание не спасет и взять интеграл аналитически бывает не под силу.

Зачем все это?

Ну раз мы не можем вывести распределение $$, почему бы не ограничиться тогда просто точечной оценкой, скажем, где плотность распределения максимальна? Ну или в крайнем случае, даже этого не делать и искать максимум $$, мы же как никак хотим построить модель, которая объясняет наши данные. Первый подход называется MAP (maximum a posterior) оценкой $$, а второй — ML (maximum likelihood) $$. Второй способ почти каждый студент технического вуза проходил в курсе теории вероятности.

У ML оценки есть ряд недостатков. Самый интуитивно понятный из них заключается в том, что даже сложная модель может казаться привлекательной с точки зрения этого критерия. Ведь чем больше вероятность, тем лучше, но с увеличением параметров модель может просто повторять данные. Этот факт вводит в заблуждение и заставляет обосновывать, почему модель адекватная. С точки зрения байесовского вывода можно предствить себе ML оценку, как MAP с $$. Да, интеграл не берется, но у нас точечная оценка и нам это не помешает, считаем плотность $$ постоянной.

Доказательство

Такого рода априорные распределения называются Improper Priors, а конкретно это — еще и Uninformative (неинформативное).

Иными словами, мы не имеем представления о том, каким должно быть $$ на самом деле. Теряется возможность использовать всю доступную информацию. К примеру:

1. Для какой-то задачи из теории достоверно известно, что $$ строго больше нуля. Это можно исправить преобразованием, но если поменять постановку на "скорее больше, чем меньше нуля", то ML это не сможет учесть.
2. Для случая линейной регрессии, когда регрессоров большое количество и есть вера в то, что не все они важны. Тогда в векторе $$ (коэффициенты) много нулевых компонент.

Стандартный подход хорош простотой реализации и изученными асимптотическими свойствами, но MAP более осмысленен в ряде ситуаций.

from theano import theano, tensor as tt
import pymc3 as pm
import pandas as pd
from sklearn import datasets
import numpy as np
from numpy import random
import pylab as plt
import seaborn as sns
import warnings
import scipy.stats as stats
warnings.filterwarnings('ignore')
%matplotlib inline
plt.mpl.style.use('ggplot')

Пример с монеткой

Давайте посмотрим, что происходит с апостериорным распределением, когда мы получаем новые наблюдения. Это очень похоже на изменение уверенности в самом обычном ее понимании. Сначала мы ничего не знаем, но когда получаем примеры, наше представление о ненаблюдаемых факторах меняется. Для наглядной репрезентации я буду использовать честный вывод апостериорного распределения.

Имея prior $$(равносильно $$) для вероятности получить "орла" $$ и имея наблюдения "орел" $$ и "решка" $$, всего $$ наблюдений, получим апостериорное распределение на вероятность $$.

Для наглядной иллюстрации потребуется несколько вспомогательных функций и синтетические данные

# первая составляет нужное распределение
def posterior(t, f):
    """
    t : орел
    f : решка
    """
    return stats.beta(a=t+1, b=f+1)

# вторая рисует график плотности
def plot_pdf(dist, ax, c):
    space = np.linspace(0, 1)
    pdf = dist.pdf(space)
    ax.plot(space, pdf, c=c, alpha=.5)
    return ax

# Данные
true_p = .3 # Истинная вероятность получить "Орла"
random.seed(42) # для воспроизводимости данных
trials = np.random.uniform(size=100) < true_p # Бинарная переменная, где 1 это орел
# Составляем пары [t, f]
observed = np.array(list(zip(np.cumsum(trials), np.arange(1, trials.size+1) - np.cumsum(trials))))
observed[:6]

array([[0, 1],
       [0, 2],
       [0, 3],
       [0, 4],
       [1, 4],
       [2, 4]])

fig, ax = plt.subplots(figsize=(15, 5))
cmap = plt.get_cmap('cool')
plot_pdf(posterior(0, 0), ax, cmap(0))
for (t, f), c in zip(observed, np.linspace(0, 1, num=observed.shape[0])):
    plot_pdf(posterior(t, f), ax, cmap(c))
plt.title('Эволюция апостериорного распределения вероятности выпадения орла')
plt.show()

Чем больше примеров мы видим, тем более узким становится апостериорное распределение, это проявление уверенности в новых знаниях. Что более интересно, так это поведение распределения при малом количестве наблюдений: оно адекватно отражает неуверенность. Этого не происходит, если пользоваться методами классической статистики и искать MLE оценку. Мы бы получали вероятность 0 для орла при малом количестве наблюдений, что, конечно, не так.

Мотивация

PyMC3 позволяет выводить апостериорное распределение без непосредственного вывода формул. Это делает возможным байесовский вероятностный вывод практически на любых адекватных моделях. Более того, с её помощью можно строить вероятностные нейронные сети, в которых вместо параметров — распределения и, следовательно, предсказания тоже являются распределениями.

Начало работы с PyMC3

Библиотека PyMC3 написана поверх Theano и поэтому может быть использована вместе с ней. Theano — библиотека для тензорной алгебры и широко используется для глубокого обучения. Она поддерживает символьные операции и дифференцирование, что и делает возможным не только обучение нейросетей с помощью backprop, но и вариационный баесовский вывод.

Работа с PyMC3 по большей части напоминает работу с Theano, в одном из наших предыдущих постов про нее хорошо написано.

Базовой частью библиотеки является модель (pm.Model), она позволяет на лету составлять апостериорную плотность (точнее ее неотнормированную часть). Для того, чтобы это работало с приятным интерфейсом, применена небольшая магия с контекстным менеджером. Латентные переменные в PyMC3 объявляются внутри контекста with model: ....

Сами латентные переменные являются переменными в смысле Theano, для них верно все то, что верно для обычных тензоров в Theano. Это полезно помнить, чтобы не бояться экспериментировать и строить более сложные модели.

Будем строить модель последовательно, чтобы на наглядном примере показать, что методы MCMC с увеличением сложности модели могут ухудшать свой результат, ну или, по крайней мере, становиться непозволительно медленными.

Сэмплировать можно с помощью вспомогательной функции pm.sample, она хорошо работает с настройками по умолчанию, но в целях демонстрации они изменены. По умолчанию для MCMC метода заранее подбираются подходящие параметры, что сейчас как раз не нужно.

# выше сделан import pymc3 as pm

with pm.Model() as simple_model:
    # По соглашению все случайные переменные должны иметь уникальные имена
    # Параметры распределения надо передавать после строкового имени
    norm = pm.Normal('norm', 0, 1)

    # не подбирать параметры для MCMC метода NUTS
    step = pm.NUTS()
    trace = pm.sample(1000, step=step)
    # Обратите внимание на количество итераций в секунду: оно будет уменьшаться по мере усложнения модели

WARNING (theano.tensor.blas): We did not found a dynamic library into the library_dir of the library we use for blas. If you use ATLAS, make sure to compile it with dynamics library.
100%|██████████| 1000/1000 [00:00<00:00, 1368.27it/s]

Trace Plot

Для визуализации результатов есть замечательные утилиты. Например, TracePlot. Это график истории марковской цепи. Анализируя ее, можно понять, насколько хорошо отработал алгоритм и требует ли он дополнительной настройки. Визуальными критериями качества являются:

1. Стационарность. Сэмплы должны образовывать шум вогруг какого-то значения.
2. Не имеют сильно выраженной автокорреляции. Иногда это может быть и ожидаемо(увидим ниже), но лучше чтобы ее не было
3. Вся история не может стостоять из одной и той же повторяющейся точки. Если какая-то переменная оставалась константой, то скорее всего что-то пошло не так в коде самой модели.

pm.traceplot(trace);

Немного усложним модель

with pm.Model() as simple_model:
    norm = pm.Normal('norm', 0, 1)
    # В качестве параметров допускается использовать уже объявленные случайные переменные
    laplace = pm.Laplace('lap', mu=norm, b=3)
    step = pm.NUTS()
    trace = pm.sample(1000, step=step)

100%|██████████| 1000/1000 [00:36<00:00, 27.10it/s]

Стала заметна турбулентность в марковской цепи для нормального распределения.

pm.traceplot(trace);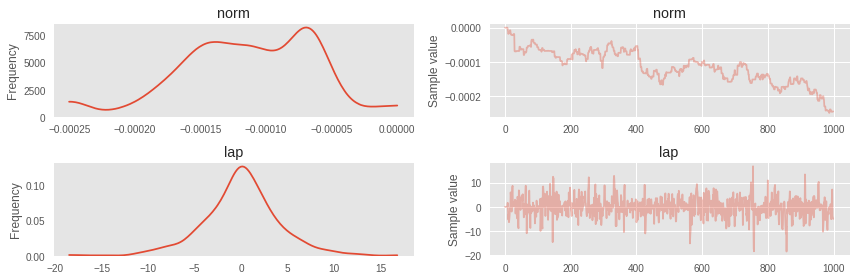

Вот что случается, когда модель становится нетривиальной, хотя должна была быть с независимой нормально распределенной первой переменой. Для таких случаев можно сначала затюнить ADVI и использовать ковариационную матрицу и средние оттуда для инициализации NUTS. Но для начала подробнее про ADVI.

ADVI

ADVI расшифровывается как Automatic Differentiation Variational Inference (ссылка на статью). Это, пожалуй, один из самых простых и часто используемых алгоритмов для приближенного байесовского вывода. Когда размерность латентного пространства растет, MCMC методы становятся либо достаточно сложными в настройке (дефолтные параметры не подходят), либо итерации занимают огромное количество времени. В том, что дефолтные параметры могут не подойти, мы убедились выше. Вот тогда и встает необходимость хотя бы приблизить целевое распределение тем, с которым мы умеем работать.

Теория

Суть метода заключается в том, что он приближает апостериорное распределение $$ другим распределением $$, для которого мы умеем считать плотность и сэмплировать. В классической постановке таким распределением является многомерное нормальное с диагональной ковариационной матрицей $$. Это является основным его недостатком: делается предположение, что латентные переменные независимы, но это, конечно же, не всегда так. Тем не менее, даже с такой сильной предпосылкой можно добиваться неплохих результатов. Далее мы увидим, как подобное упрощение позволяет экономить вычислительные ресурсы.

Постановка задачи

Пусть есть наблюдения $$, параметрическая модель с параметрами $$ и функция ее правдоподобия $$. Помимо этого, байесовский подход требует наличия априорного распределения на параметры модели $$. По правилу Байеса выводим апостериорное распределение на параметры:

Часть без нормализующей константы посчитать обычно не составляет труда:

Зададим параметрическое семейство распределений $$, с которым будем работать.

Метрика. Стандартным выбором для метрики в пространстве распределений является расстояние Кульбака-Лейблера

Если распределения совпадают, то матожидание равняется нулю, в противном случае матожидание больше нуля. Таким образом, задача байесовского вывода сводится к задаче оптимизации

Решение задачи

Эта задача решается стохастическим градиентным спуском. Для этого необходимо взять производную по $$.

Мы полностью разложили KL-метрику, и поскольку ее надо минимизировать, а $$ все равно константа, то и считать ее нет необходимости. Так мы избавляемся от основной проблемы аналитического вывода апостериорного распределения — неберущегося интеграла. Все, что осталось, равняется $\$inline\$-ELBO\$inline\$$ (Evidence Lower BOund).

Казалось бы, дальше все задано аналитически и хорошо считается, но есть одно но. Чтобы взять производную по параметрам, придется взять производную по интегралу, который, в свою очередь, зависит от этих самых параметров. Если мы будем делать это методами MC и аппроксимировать интеграл несколькими сэмплами, то столкнемся с тем, что градиенты имеют большую дисперсию. Этого можно избежать, и выбранное нами семейство апостериорных распределений это позволяет сделать. Следующая теорема продемонстерирует условия, когда производную можно внести под знак интеграла.

Теорема

Пусть $$ случайная величина с плотностью распределения $$ и пусть $$, где $$ — детерминистская обратимая функция. Пусть плотность распределения случайной величины $$ это $$. Предположим далее, что $$.
Тогда для функции $$ с производной по $$ выполнено

Это и понадобится для оптимизации. Поскольку $$ представима в виде $$, где $$. Пусть $$

Это называется Reparametrization Trick. Используя его, уже гораздо проще взять производную от $$.

Cделав соответствующую репараметризацию, будет достаточно вызвать theano.grad на выражение и получить градиент выше, точнее его единственоый сэмпл, которого вполне достаточно. После этого можно использовать любимый оптимизатор.

with pm.Model() as simple_model:
    norm = pm.Normal('norm', 0, 1)
    laplace = pm.Laplace('lap', mu=norm, b=3)
    trace = pm.sample(1000, init='advi', n_init=10000)

Auto-assigning NUTS sampler...
Initializing NUTS using advi...
Average ELBO = -0.11837: 100%|██████████| 10000/10000 [00:00<00:00, 13764.87it/s]
Finished [100%]: Average ELBO = -0.1085
Evidence of divergence detected, inspect ELBO.
100%|██████████| 1000/1000 [00:01<00:00, 974.36it/s]

Уже гораздо лучше.

HINT: на трейсплоте важно смотреть на марковскую цепь, в идеале она должна быть стационарной, примерно как здесь, и не сильно турбулентной, как выше

pm.traceplot(trace);

with pm.Model() as simple_model:
    norm = pm.Normal('norm', 0, 1)
    laplace = pm.Laplace('lap', mu=norm, b=3)
    # использование произвольных выражений (даже таких экзотических) тоже допустимо
    lognorm = pm.Lognormal('lognorm', sd=norm**2 + 1e-7, testval=1)
    trace = pm.sample(10000, n_init=40000)

Auto-assigning NUTS sampler...
Initializing NUTS using advi...
Average ELBO = -7.4197e+05: 100%|██████████| 40000/40000 [00:03<00:00, 11614.15it/s]
Finished [100%]: Average ELBO = -1.221e+08
Evidence of divergence detected, inspect ELBO.
100%|██████████| 10000/10000 [01:06<00:00, 150.87it/s]

Здесь видно, что есть заметная автокорреляция в первой марковской цепи. На самом деле неудивительно, ведь из-за того, что мы использовали квадрат нормального распределения как стандартное отклонение, NUTS застревал в локальных максимумах плотности.

# первые 100 итераций портят картинку
pm.traceplot(trace[100:]);

Модель можно составлять последовательно, необязательно сразу в одном контексте:

random.seed(42)
obs = random.normal(0, 1, size=10) + random.normal(0, 10, size=10)
with pm.Model() as model:
    hc = pm.HalfCauchy('hc', beta=1)
# your code
with model:
    # если есть наблюдаемые переменные, то они указываются через ключевое слово
    norm = pm.Normal('norm', 0, hc, observed=obs)

with model:
    trace = pm.sample(1000, tune=200, n_init=1000)
pm.traceplot(trace[10:]);

Auto-assigning NUTS sampler...
Initializing NUTS using advi...
Average ELBO = -1,954.7: 100%|██████████| 1000/1000 [00:00<00:00, 8967.46it/s]
Finished [100%]: Average ELBO = -1,402.2
100%|██████████| 1000/1000 [00:00<00:00, 1464.22it/s]

Идеология PyMC3 предусматривает проверку модели на валидность по ходу построения: так избегаются ошибки на раннем этапе. Это достигается принудительным использованием test_value

norm.tag.test_value

array([ -4.13746262,  -4.79556179,   3.06731129, -17.60977173,
       -17.48333168,  -5.85701227,  -8.54909801,   3.90990806,
        -9.54971504, -13.58047676], dtype=float32)

Theano идеально подходит для векторизованных операций. Поэтому, если перед вами стоит выбор, как задавать модель — через цикл или через создание веторной случайной переменной, — лучше выбрать второй вариант. В этом случае создаются независимые случайные переменные, к которым можно впоследствии обращаться по индексам.

with pm.Model() as model:
    vectorized_p = pm.Uniform('p', shape=(4,))
vectorized_p.tag.test_value

array([ 0.5,  0.5,  0.5,  0.5], dtype=float32)

Если вам не нравится инициализация по умолчанию, вы можете указать свою.

with pm.Model() as model:
    vectorized_p = pm.Uniform('p', 
                              shape=(4,), 
                              testval=np.ones((4,), 'float64') * .3, 
                              dtype='float64')
vectorized_p.tag.test_value

array([ 0.3,  0.3,  0.3,  0.3])

Байесовская линейная регрессия

Первый более менее большой и осмысленый пример будет про цены на бостонские квартиры:

data_ = datasets.load_boston()
data = pd.DataFrame(data=data_['data'], columns=data_['feature_names'])
y = data_['target']

print('\n'.join(data_.DESCR.splitlines()[13:28]))

    :Attribute Information (in order):
        - CRIM     per capita crime rate by town
        - ZN       proportion of residential land zoned for lots over 25,000 sq.ft.
        - INDUS    proportion of non-retail business acres per town
        - CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
        - NOX      nitric oxides concentration (parts per 10 million)
        - RM       average number of rooms per dwelling
        - AGE      proportion of owner-occupied units built prior to 1940
        - DIS      weighted distances to five Boston employment centres
        - RAD      index of accessibility to radial highways
        - TAX      full-value property-tax rate per $10,000
        - PTRATIO  pupil-teacher ratio by town
        - B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
        - LSTAT    % lower status of the population
        - MEDV     Median value of owner-occupied homes in $1000's

data.head()

Создадим простую байесовскую линейную модель.

По умолчанию Prior на коэффициенты — Normal(mu=0, tau=1.0E-6), на константу — Flat.
Оценивать модель будем с помощью SVGD для разнообразия.

from functools import partial
with pm.Model() as lm_model: 
    lm_model = pm.GLM(x=data, y=y)
    # для вариационных методов есть унифициорванный интерфейс через pm.fit
    histogram = pm.fit(200, method='svgd', obj_optimizer=partial(pm.adagrad, learning_rate=.7))

100%|██████████| 200/200 [00:05<00:00, 35.31it/s]

И вот, мы получили распределение! По нему теперь можно строить доверительные интервалы, что мы и сделаем для коэффициентов при наших регрессорах.

# метод `histogram.sample` создает аналогичный объект, что мы получали с помощью pm.sample. 
# Это просто набор случайных реализаций из приближенного распределения
pm.forestplot(histogram.sample(300), varnames=data.columns);

Байесовские нейронные сети

Поскольку бэкенд PyMC3 — Theano, то совершенно естественным желанием будет использовать вариационный байесовский вывод для нейронных сетей. Это довольно легко и прозрачно получается с помощью Lasagne.

Отличительной особеностью байесовской нейронной сети от обычной является то, как моделируются веса. В привычном случае в качестве весов берутся конкретные значения и оптимизируются с помощью градиентного спуска.

В случае с байесовской нейронной сетью все иначе. Веса сети воспринимаются как ненаблюдаемые случайные переменные с априорным распределением. В идеале на них надо сделать честный байесовский вывод, но мы видели, что сэмплирование тормозит даже самые простые задачи, а тут совершенно иной уровень. Обычной практикой при обучении байесовских сетей является приближенный вариационный вывод этого самого распределения. Наиболее быстрым из вариационных методов является вышеупомянутый ADVI. Им и будем пользоваться тут.

from lasagne.layers import *
import lasagne
from sklearn import datasets
from sklearn.preprocessing import scale
from sklearn.cross_validation import train_test_split
from sklearn.datasets import make_moons

Сгенерируем синтетические данные с помощью утилит sklearn

X, Y = make_moons(noise=0.2, random_state=0, n_samples=1000)
X = scale(X)
# дополнительно надо поменять тип, иначе X и Y float64
X = X.astype(theano.config.floatX)
Y = Y.astype(theano.config.floatX)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=.5)

fig, ax = plt.subplots()
ax.scatter(X[Y==0, 0], X[Y==0, 1], color='b', label='Class 0')
ax.scatter(X[Y==1, 0], X[Y==1, 1], color='r', label='Class 1')
sns.despine(); ax.legend()
ax.set(xlabel='X', ylabel='Y', title='Toy binary classification data set');

Для Lasagne в качестве инициализации можно передавать функцию, возвращающую символьную переменную theano. Инициализация сильно отличается от PyMC3, поэтому придется написать свой адаптер.

import itertools
class RandomWeight(object):
    counter = itertools.count(0)
    def __init__(self, mu=0, sd=1):
        self.mu = mu
        self.sd = sd

    def __call__(self, shape):
        name = 'auto_%s' % next(self.counter)
        return pm.Normal(name, self.mu, self.sd, 
                      testval=lasagne.init.GlorotUniform()(shape),
                      shape=shape, dtype=theano.config.floatX)

Создавать нейронную сеть необходимо в контексте модели, чтобы веса инициализировались корректно

input_var = theano.shared(X_train)
out_var = theano.shared(Y_train)
with pm.Model() as nnet:
    inp = InputLayer((None, 2), input_var)
    # без констант сеть работает неплохо, можно на нее тут забить
    z = DenseLayer(inp, 5, W=RandomWeight(), b=None, nonlinearity=tt.tanh)
    z = DenseLayer(z, 5, W=RandomWeight(), b=None, nonlinearity=tt.tanh)
    p = DenseLayer(z, 1, W=RandomWeight(), b=None, nonlinearity=tt.nnet.sigmoid)
    # вместо функции потерь тепеть наблюдаемая случайная величина, ее -p(D|z) будет играть роль потерь
    pm.Bernoulli('observed', p=get_output(p).flatten(), observed=out_var)

Приближенный байесовский вывод для такой модели можно делать с помощью вышеописанного ADVI

with nnet:
    inference = pm.ADVI()
    approx = inference.fit(30000)

Average Loss = 132.78: 100%|██████████| 30000/30000 [00:35<00:00, 847.38it/s] 
Finished [100%]: Average Loss = 132.78

plt.figure(figsize=(12, 6))
plt.plot(inference.hist, alpha=.3)
plt.legend()
plt.ylabel('-ELBO')
plt.xlabel('iteration');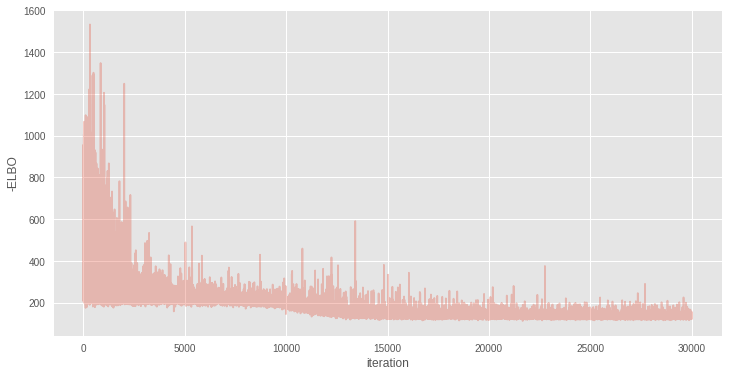

Результаты можно с легкостью переиспользовать для другой задачи, например, использовать их, чтобы делать предсказания:

# Создаем символьный вход
x = tt.matrix('X')
# Переменную количества сэмплов
n = tt.iscalar('n')
# В конфиге теано стоит compute_test_value='raise', чтобы он не ругался, зададим тестовые значения в переменные
x.tag.test_value = np.empty_like(X_train[:10])
n.tag.test_value = 100
# У любого класса аппроксимации есть методы sample_node и apply_replacements
# Они убирают зависимость графа от латентных переменных pymc3 и заменяют их аппроксимацией
_sample_proba = approx.sample_node(get_output(p).flatten(), size=n,
                                   more_replacements={input_var:x})
# Вот теперь можно скомпилировать функцию
# У аппроксимаций нет апдейтов генератора случайных чисел, это удобно 
sample_proba = theano.function([x, n], _sample_proba)

Собственно сами предсказания можно получить, вызвав функцию на тестовом множестве:

pred = sample_proba(X_test, 500).mean(0) > 0.5

fig, ax = plt.subplots()
ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1], color='b')
ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r')
sns.despine()
ax.set(title='Predicted labels in testing set', xlabel='X', ylabel='Y');

Разделяющая граница

Можно посмотреть разделяющую границу для классов, для этого можно подставить туда все точки на плоскости и усреднить.

grid = np.mgrid[-3:3:100j,-3:3:100j].astype('float32')
grid_2d = grid.reshape(2, -1).T
ppc = sample_proba(grid_2d ,500)

cmap = sns.diverging_palette(250, 12, s=85, l=25, as_cmap=True)
fig, ax = plt.subplots(figsize=(16, 9))
contour = ax.contourf(grid[0], grid[1], ppc.mean(axis=0).reshape(100, 100), cmap=cmap)
ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1], color='b')
ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r')
cbar = plt.colorbar(contour, ax=ax)
_ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel='X', ylabel='Y');
cbar.ax.set_ylabel('Posterior predictive mean probability of class label = 0');

Уверенность модели

Уверенность модели в предсказаниях — очень интересная штука. Обычно в моделях мы можем получить только точечную оценку на интересующее нас значение. Она сама по себе не несет в себе информации о том, как хорошо модель понимает окружающий мир: об этом может сказать только распределение оценки. С помощью байесовских методов это делается очень интуитивно, и, более того, довольно неплохо реализовано в PyMC3.

cmap = sns.cubehelix_palette(light=1, as_cmap=True)
fig, ax = plt.subplots(figsize=(16, 9))
contour = ax.contourf(grid[0], grid[1], ppc.std(axis=0).reshape(100, 100), cmap=cmap)
ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1], color='b')
ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r')
cbar = plt.colorbar(contour, ax=ax)
_ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel='X', ylabel='Y');
cbar.ax.set_ylabel('Uncertainty (posterior predictive standard deviation)');

Это далеко не все вещи, которые можно делать с помощью PyMC3. За кадром остались байесовская оптимизация, гауссовские процессы, LDA и многое другое.

В репозитории PyMC3 есть огромное количество примеров, которые можно запустить у себя. Все они в виде jupyter тетрадок вот здесь

Ссылки на используемые источники

• Bayesian Methods for Hackers
• Weight Uncertainty in Neural Networks
• Пример с монеткой
• Automatic Differentiation Variational Inference
• Operator Variational Inference
• Stein Variational Gradient Descent
• Полная тетрадка с нейронной сетью
• ссылка на jupyter ноутбук с этой публикацией

Благодарности

Хочу сказать большое спасибо mephistopheies и bauchgefuehl за помощь в подготовке публикации.