Прогнозирование временных рядов с помощью AutoML
- понедельник, 31 мая 2021 г. в 00:33:55
Хабр, привет!
В лаборатории моделирования природных систем Национального центра когнитивных разработок Университета ИТМО мы активно исследуем вопросы применения автоматического машинного обучения для различных задач. В этой статье мы хотим рассказать о применении AutoML для эффективного прогнозирования временных рядов, а также о том, как это реализовано в рамках open-source фреймворка FEDOT. Это вторая статья из серии публикаций, посвященной данной разработке (с первой из них можно ознакомиться по ссылке).
Все подробности — под катом!
Современная Data Science стала весьма востребованной частью IT сферы. Специалисты собирают данные, занимаются их очисткой, пробуют различные модели, производят валидацию, выбирают лучшие из них. И все это для того, чтобы предоставить бизнесу решение, которое принесет наибольшую пользу. При этом, некоторые этапы получения таких решений с каждым годом все больше и больше автоматизируются. Как правило, это касается наиболее рутинных частей. Таким образом освобождается время экспертов для более важных задач.
Итак, представим, что перед специалистом стоит задача построить модель машинного обучения и “обернуть” её в web-сервис, чтобы эта самая модель выполняла полезную работу — предсказывала что-либо. Но прежде чем дойти до этапа обучения модели, требуется пройти несколько шагов, в том числе:
Такие многоступенчатые последовательности операций, включающие этапы от первичной обработки данных до обучения модели и составления прогнозов, называют пайплайнами. Работать с пайплайнами уже несколько сложнее, чем с одиночными моделями машинного обучения, так как чем больше составных блоков, тем больше гиперпараметров, которые нужно оптимизировать. Также выше вероятность того, что на каком-нибудь этапе возникнет ошибка, да и в целом такую более громоздкую систему труднее настраивать и контролировать ее поведение. Для решения этой проблемы реализованы специальные инструменты — MLFlow, Apache AirFlow и т. д — что-то вроде workflow management system (WMS) в мире машинного обучения. Они призваны упростить контроль за состоянием пайплайнов обработки данных.
Почему потребность в таких инструментах возникла, ведь раньше обходились без них?
Ответ в том, что отрасль “взрослеет”, появляются хорошо оптимизированные решения для общих задач. Постепенно индустрия уходит от самописных “сервисов” и переходит к использованию стандартных подходов и технологий к обработке данных для ML задач.
Более амбициозной задачей в данной области машинного обучения является автоматическая генерация этих пайплайнов. Существует несколько фреймворков, которые предоставляют подобные функции, среди open-source, например это TPOT, AutoGluon, MLJAR или H2O. Такие AutoML фреймворки решают задачу оптимизации вида “построить такой пайплайн, который дает конечный прогноз с наименьшей (среди всех рассмотренных решений) ошибкой”. В основном структура пайплайна зафиксирована и подбираются только гиперпараметры, но некоторые фреймворки способны получать в качестве решения модели произвольной структуры. Данная оптимизационная задача (нахождения пайплайна произвольной структуры) решается как правило при помощи эволюционных алгоритмов, примеры: фреймворки TPOT и FEDOT.
Существуют также и проприетарные SaaS-решения, такие как DataRobot, GoogleAutoTables, Amazon SageMaker, которые помогают не только автоматизировать ML эксперименты, но и предоставляют возможности AutoML.
Как правило, AutoML библиотеки и сервисы успешно решают две самые популярные задачи в машинном обучении: классификация и регрессия на табличных данных. Реже поддерживаются задачи, связанные с обработкой изображений, текста и прогнозирования временных рядов. В рамках данной статьи мы не будем рассматривать плюсы и минусы известных решений, а остановимся на возможностях автоматического машинного обучения в задаче прогнозирования временных рядов.
Несмотря на то, что задача прогнозирования довольно востребована в науке и бизнесе, большая часть open-source библиотек автоматического машинного обучения не предоставляют возможностей для формирования пайплайнов для задачи прогнозирования временных рядов. Причин тому может быть несколько, одна из которых — сложность в адаптации текущей функциональности библиотеки для прогнозирования рядов без переработки инструментария для других задач (классификации и регрессии).
Дело в том, что обработка временных рядов отличается от привычного набора действий при решении задачи регрессии. Отличия начинаются уже с разбиения исходной выборки: так например, перемешивать данные в случайном порядке для валидации модели временного ряда настойчиво не имеет смысла. По другому для временных рядов формируются и признаки: на исходном ряде, как правило, модели машинного обучения не обучают — его требуется перевести в другое представление. Внедрять такие конструкции в уже существующий AutoML проект со своим legacy бывает проблематично — скорее всего, именно поэтому разработчики часто отказываются от временных рядов (чтобы “не гнаться за двумя зайцами”) и концентрируются на обработке конкретных типов данных: только табличных, или только текста.
Некоторые команды, которые все-таки решаются поддерживать прогнозирование временных рядов, однако — ограничиваются только этим типом данных. Хороший open-source пример — фреймворк AutoTS. В подобных библиотеках обычно используются “классические” статистические модели для прогнозирования — например AR или ARIMA. “Внутри” фреймворка производится настройка этих моделей, а затем выбирается наилучшая (по метрике ошибки на валидационной выборке), но новых моделей здесь не генерируются. На такой логике, например, основана библиотека pmdarima.
Другой способ — адаптировать функциональность готового AutoML-инструмента для задачи прогнозирования. На эту роль хорошо подходят регрессионные модели. Так, например, было сделано в H2O, где в своей коммерческой версии продукта разработчики предоставили такую возможность. Однако, судя по некоторым примерам использования open-source версии, пользователю придется взять на себя задачу первичной обработки исходных рядов, например, извлечение признаков. Для полноценной работы такого урезанного инструментария может не хватать.
А какие функции хотелось бы иметь в AutoML-арсенале?
Хотя задача прогнозирования поведения одномерного массива выглядит тривиальной, существует множество инструментов, которыми инженер хотел бы обладать при работе с временными рядами. Например:
- Возможность строить интерпретируемые ансамбли из моделей (например, чтобы одна модель воспроизводила высокочастотную составляющую временного ряда, вторая — низкочастотную, а третья — объединяла их прогнозы);
- Иметь возможность осуществлять настройку гиперпараметров в пайплайнах для временных рядов;
- Использовать экзогенные (вспомогательные) временные ряды;
- Применять специфические методы предобработки (от сглаживания скользящим средним до преобразования Бокса-Кокса);
- Иметь возможность применять in-sample и out-of-sample прогнозирование;
- А если временной ряд с пропусками — как их устранить?
Учесть все перечисленные возможности в одном фреймворке, и, при этом, не ограничиваться только временными рядами — достаточно сложная задача.
Такие требования к AutoML появились не просто так. Мы работаем в лаборатории моделирования природных систем, и последние несколько лет участвовали в десятках различных исследовательских и бизнес проектах в области машинного обучения, data-driven моделирования, оптимизации и д.р. Нам на практике часто приходится решать подобные проблемы, в т.ч. для прогнозирования пространственно-временных данных.
Наша лаборатория является частью Национального центра когнитивных разработок — центре компетенций по машинному обучению и когнитивным технологиям, созданном в 2018 году на базе Университета ИТМО. Благодаря данному центру и стало возможным осуществление проекта создания фреймворка FEDOT — мы занимаемся им с начала 2020 года.
Некоторое время назад мы заинтересовались исследованиями в области AutoML, а в команде появились свежие идеи для экспериментов. В итоге, идеи сформировались в полноценный open-source AutoML фреймворк, который мы разрабатываем и поддерживаем в лаборатории — FEDOT.
Основная мотивация заключалась в том, чтобы разработать удобный инструмент, который упростил бы процесс создания пайплайнов для решения широкого круга задач — полезный в том числе и для нас самих. Мы хотели встроить модели разной природы в такие пайплайны, например, не только модели машинного обучения и операции предобработки, но еще и предметные модели из различных областей (например, гидродинамические модели). Такой подход часто называют гибридным моделированием.
Еще хотелось бы автоматически решать более одной задачи в рамках одного пайплайна, то есть задачу регрессии совместно с задачей прогнозирования временного ряда, или одновременно задачу регрессии и классификации. Например, в задаче кредитного скоринга, т.е. бинарной классификации потенциальных заемщиков, можно использовать не только анкетные признаки, но и будущие значения денежного потока, который можно попробовать спрогнозировать как временной ряд. Весьма перспективно, на наш взгляд, было бы получать baseline для таких задач автоматически.
Так же нам было интересно исследовать методы идентификации пайплайнов произвольной структуры и использовать многокритериальную оптимизацию, позволяющую оптимизировать не только ошибку моделирования, но и сложность найденного решения (её, например, можно оценить через общее количество блоков в пайплайне).
В некоторых из этих задач нам удалось получить интересные результаты, и если интересно, научные статьи по ним вы можете посмотреть здесь и здесь. Ниже мы сфокусируемся на задаче прогнозирования временных рядов и разберем, как там можно использовать AutoML и FEDOT, в частности.
Ранее мы говорили про пайплайны для решения задач машинного обучения. Пайплайн, строго говоря, представляет собой ациклический направленный граф. В терминах FEDOT, этот граф называется цепочка, или композитная модель.
Основные абстракции, которыми оперирует FEDOT во время работы, это:
Приведенные абстракции можно увидеть на рисунке ниже:
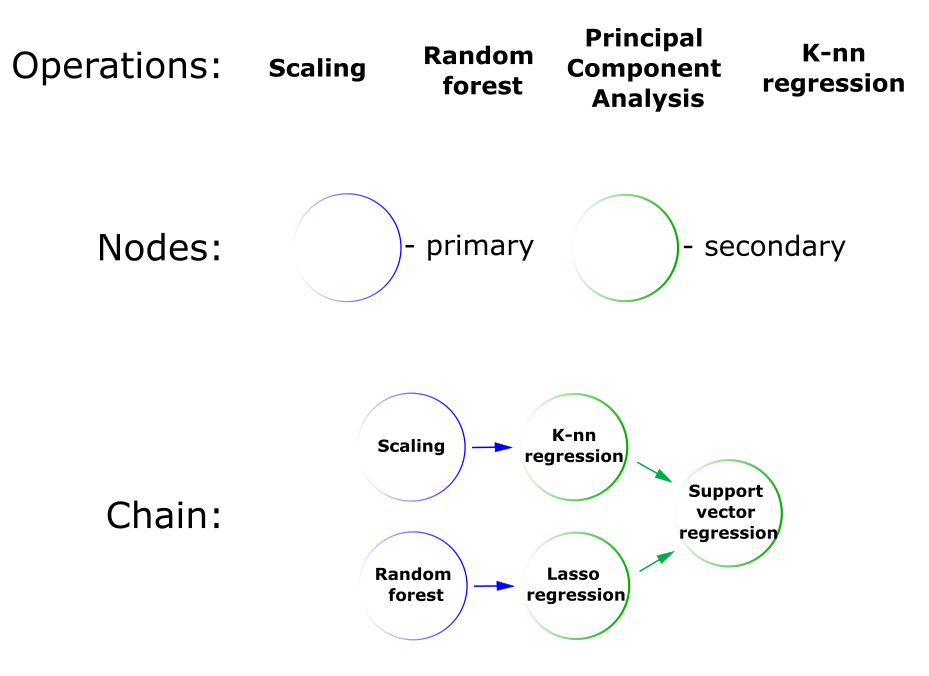
Операции, узлы и цепочки в фреймворке FEDOT
В качестве моделей в структуру такого пайплайна могут встраиваться как модели машинного обучения, так и классические, например, авторегрессия для временных рядов.
Здесь еще нет автоматического машинного обучения. Фреймворк “оживает”, когда запускается его интеллектуальная часть — композер. Композер — это интерфейс для составления цепочек. Внутри него используется тот или иной метод оптимизации — который и реализует “автоматическую” часть AutoML. По умолчанию в фреймворке используется эволюционный подход, основанный на принципах генетического программирования. Однако, при необходимости в композер может быть добавлен любой поисковый алгоритм — от случайного поиска до байесовской оптимизации.
Окей, решать задачи классификации или регрессию мы умеем. И даже представляем как в FEDOT-е составлять цепочки из моделей для этого. Но как теперь перейти к прогнозированию временного ряда? И как здесь можно использовать, например, решающее дерево? Признаки то где?
Признаки есть! Только для формирования таблицы с признаками нужно пройти по временному ряду скользящим окном и подготовить траекторную матрицу.
Стоит сказать, что представление временного ряда в такой форме — это не наше изобретение: можете почитать про SSA метод, в котором используется данное преобразование. Данный подход используется также и в одной из версии библиотеки H2O. Применение почти всех моделей машинного обучения для временных рядов сводится к построению таких матриц.
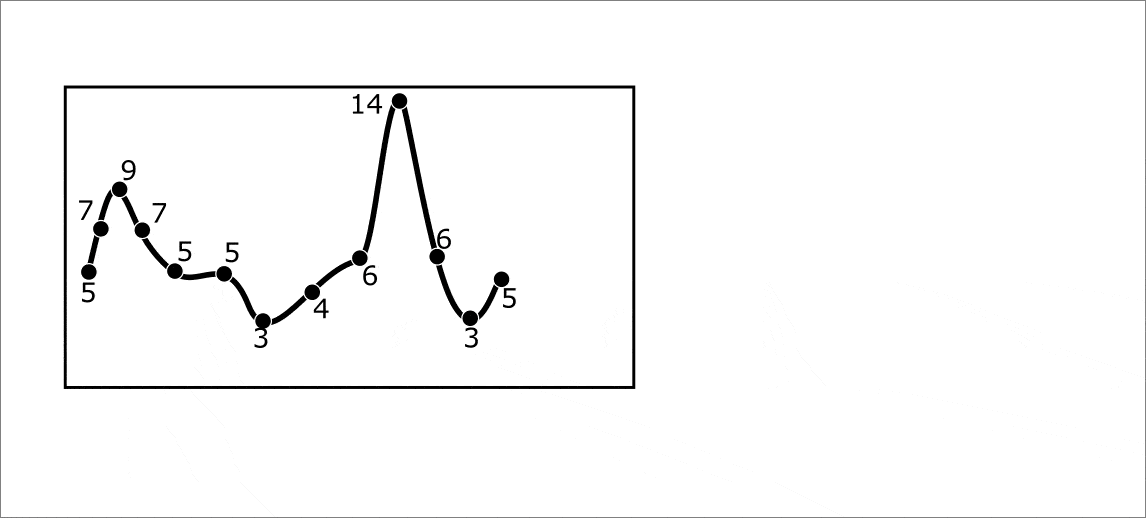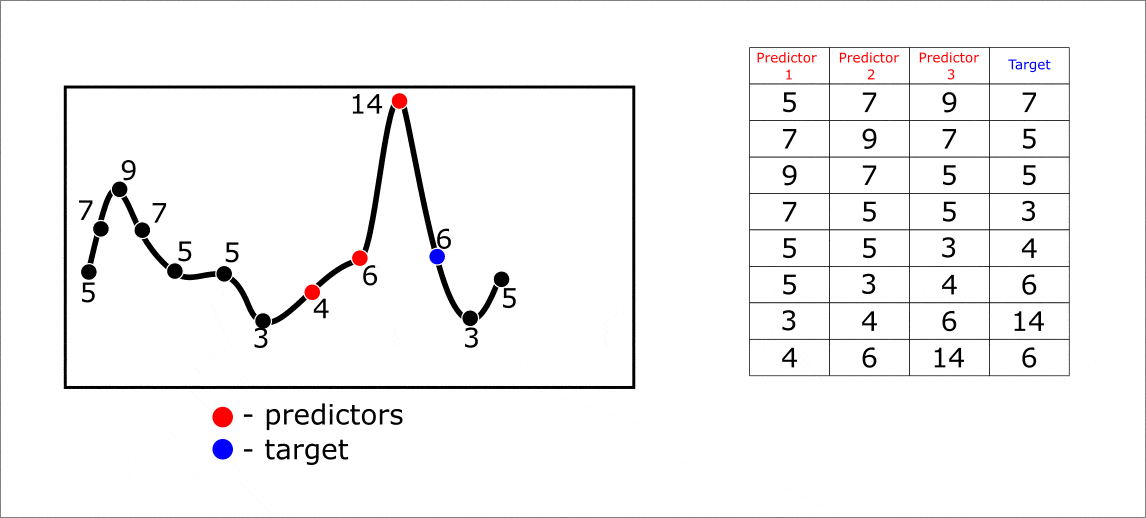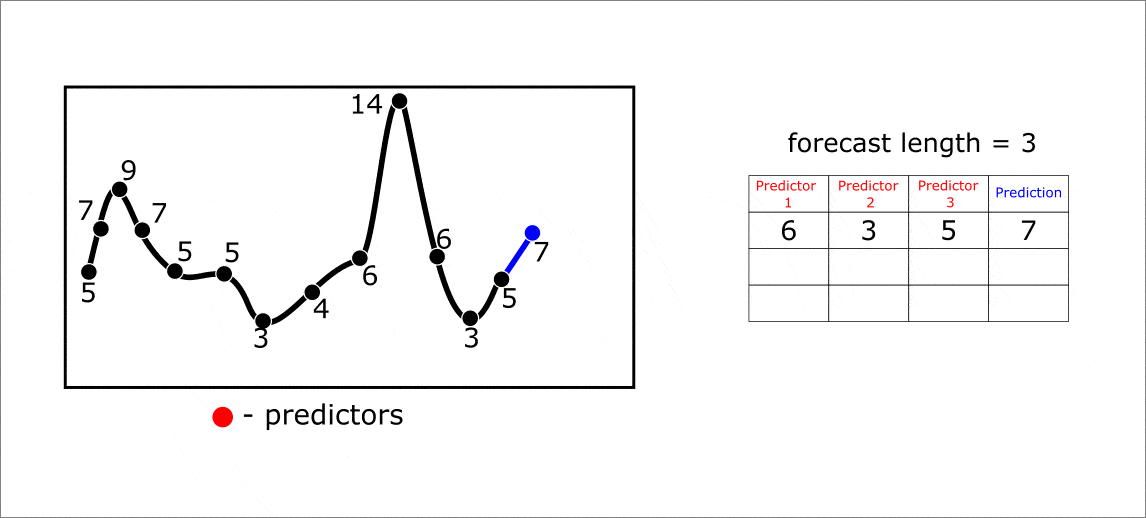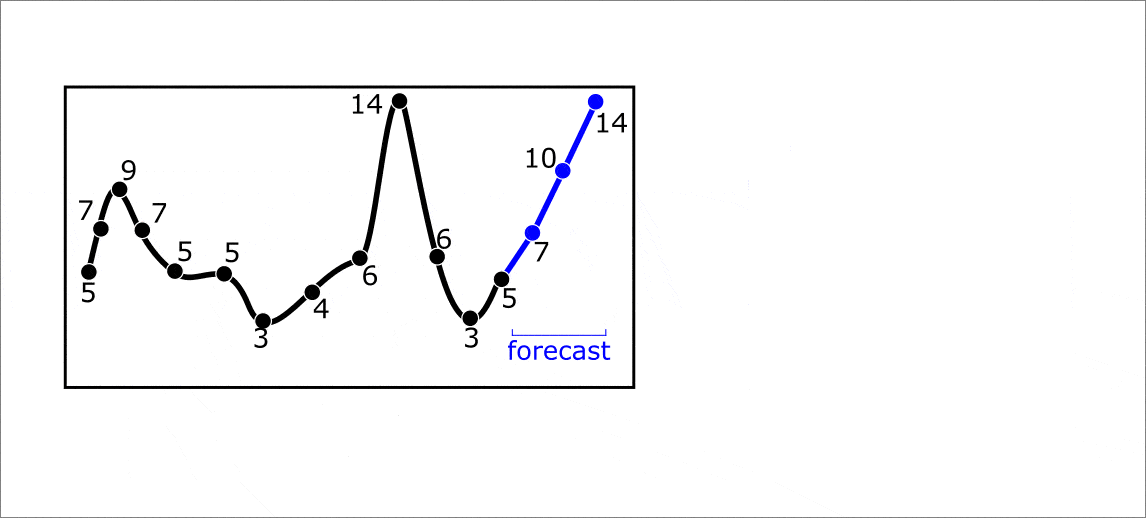
Разберем этот способ преобразования ряда подробнее. Временной ряд — это последовательность значений, где последующие значения обычно зависят от предыдущих. Значит, мы можем использовать текущие и предыдущие элементы временного ряда для прогнозирования будущих. Представим, что мы хотим спрогнозировать ряд на один элемент вперед, используя текущее и одно предыдущее значение:

Пример составления таблицы с признаками для прогнозирования временного ряда
Такое преобразование мы будем называть “lagged-преобразование“ временного ряда. В FEDOT мы вынесли его в отдельную операцию “lagged”. Его важным гиперпараметром является размер скользящего окна — от него зависит сколько предыдущих значений мы будем использовать в качестве предикторов.
Ниже приведена анимация с примерам многошагового прогнозирования на 1 элемент вперед. Однако, прогноз за один шаг может осуществляться сразу на несколько элементов вперед. В таком случае решается задача muli-target регрессии. Весь процесс прогнозирования от формирования траекторной матрицы до составления предсказания можно увидеть на анимации ниже:
Анимация. Прогнозирование на 3 элемента вперед при помощи lagged преобразования временного ряда
В качестве модели для прогнозирования может быть использована любая модель машинного обучения. Однако в фреймворк встроены также и специфические модели для прогнозирования временных рядов, такие как AR и ARIMA. Также реализованы методы предобработки, вроде сглаживания скользящим средним или сглаживания Гаусса.
В сообществе распространены примеры прогнозирования временных рядов на довольно простых примерах. Один из самых популярных — временной ряд “US airline passengers” и выглядит следующим образом:
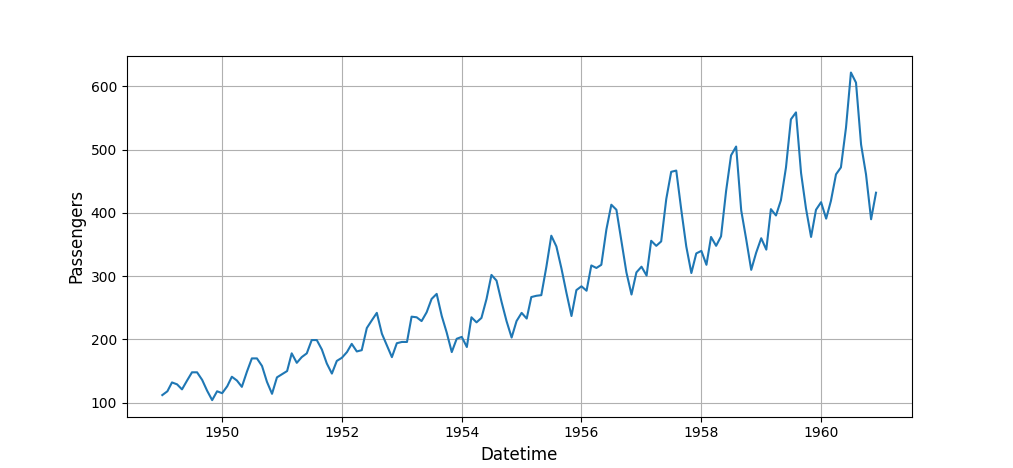
Демонстрировать возможности библиотеки на таких рядах очень заманчиво — однако, практически любая сколько-нибудь сложная модель сможет достойно показать себя здесь. Мы же решили взять ряды посложнее, из промышленности, чтобы проверить на них AutoML на прочность. Надеемся, этот пример будет показательным.
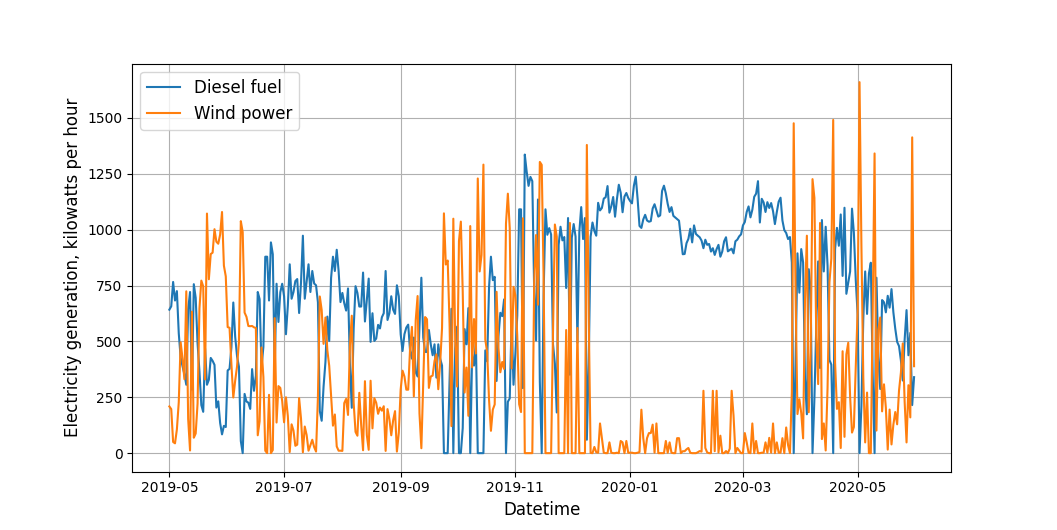
Имеются два временных ряда: первый — это среднесуточная выработка электроэнергии ветряной установкой. Другой — среднесуточная выработка электроэнергии при помощи дизельного генератора. Оба показателя измеряются в кВт⋅ч.
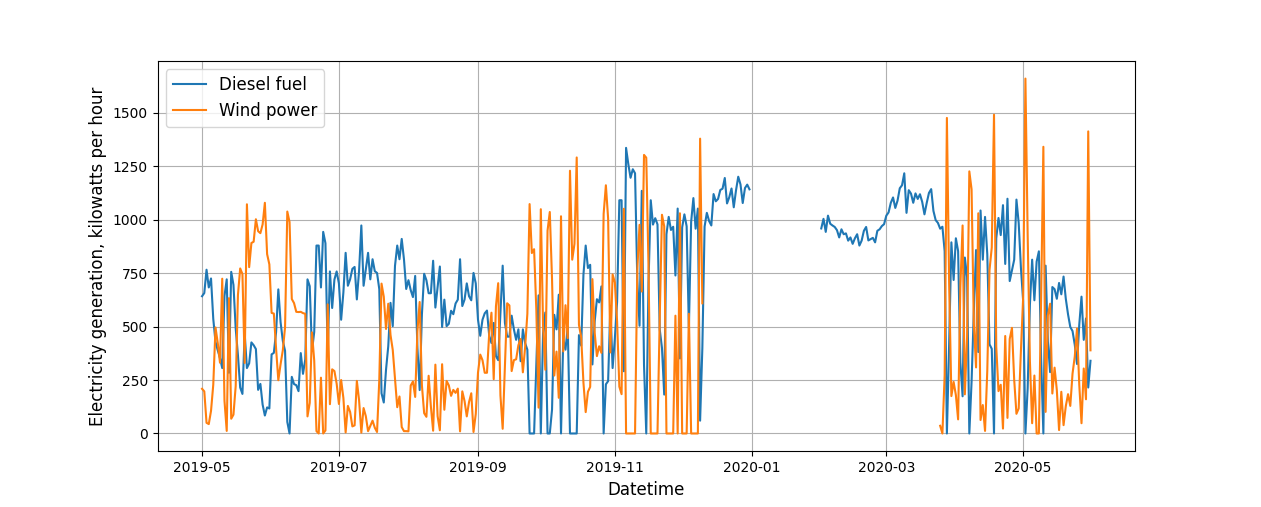
Выработка электроэнергии при помощи дизельной установки и ветряного электрогенератора
Работа ветряного электрогенератора зависит от скорости ветра, и если она снижается, то для поддержки выработки электроэнергии на достаточном уровне используется дизельный генератор. Отсюда и прослеживается поведение временных рядов — когда выработка электроэнергии на ветряке падает, на дизельном генераторе она растет, и наоборот. Стоит также заметить, что временные ряды имеют пропуски.
Нам необходимо прогнозировать нагрузку на дизельный генератор на 14 дней вперед. Таким образом, целевая переменная — выработка энергии дизельным генератором.
Ниже не будут приведены листинги кода, так как иначе статья может растянуться. Однако, для лучшего восприятия мы подготовили большое количество визуализаций. Полная версия кода, где все технические моменты расписаны гораздо более подробно, расположена в jupyter notebook’е.
Первая проблема — это пропуски в рядах. В FEDOT для восстановления значений во временных рядах мы реализовали три группы методов:
Первые, как правило, работают быстро, но не дают большой точности. Методы из второй группы не учитывают специфику задачи и эквивалентны просто прогнозированию временного ряда. Последняя группа методов учитывают недостатки предыдущих. Именно их мы и будем применять далее. Для заполнения пропусков при помощи композитной модели используется двусторонний прогноз временного ряда.

Пример комбинированного прогноза, где для прогноза используются две модели, а результат их прогноза комбинируется при помощи взвешенного среднего
Для этого мы строим простую цепочку из lagged-представления, сглаживания Гаусса, и ridge-регрессии (см. рисунок), обучаем ее предсказывать значения ряда “вперед”.
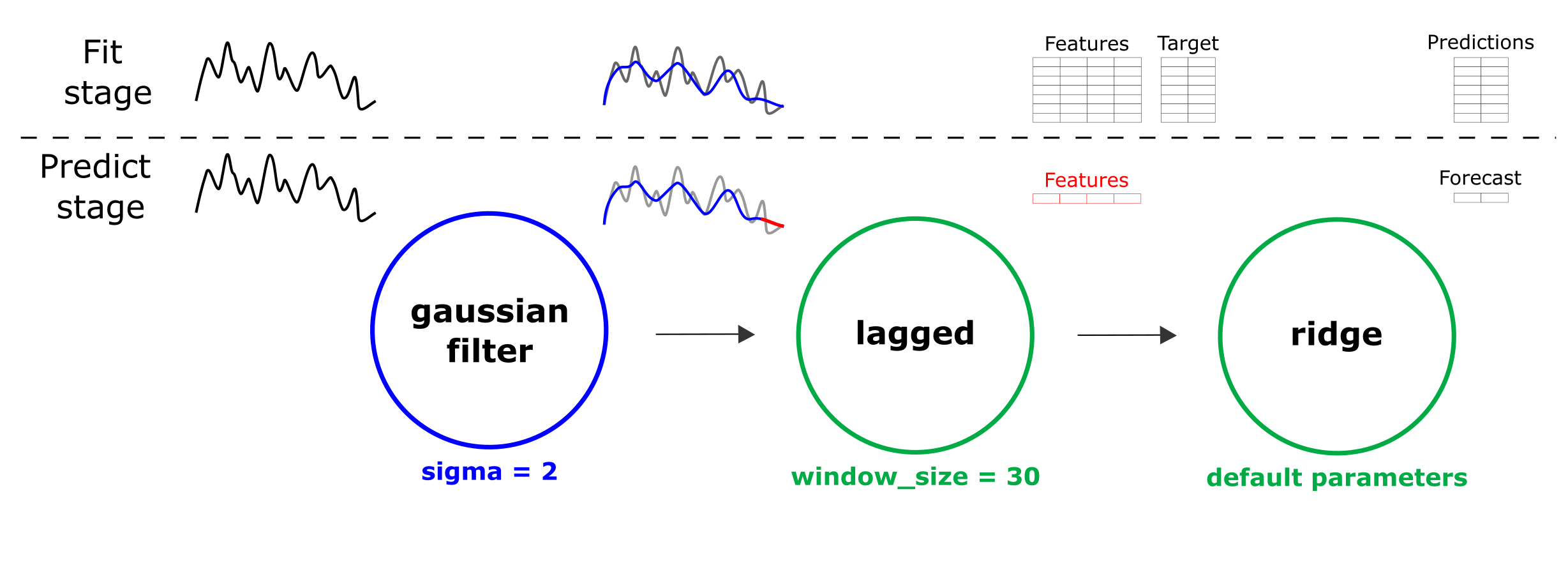
Структура применяемой цепочки для восстановления пропусков во временном ряде
По аналогии, повторяем это для обратного направления — обучаем цепочку прогнозировать “прошлое”. Комбинируем два прогноза, получаем усредненный ряд, которым мы заполним пропуск.
Последовательность действий при таком подходе может быть описана так. Сначала, используется часть временного ряда, расположенная слева от пропуска. На этом участке временного ряда обучается композитная модель, с помощью которой формируется прогноз на такое количество элементов вперед, сколько их есть в пропуске. После этого процедура повторяется для правой (относительно пропуска) части. Для этого известная часть временного ряда инвертируется — обучается модель и формируется прогноз — прогноз инвертируется. Комбинация прогнозов осуществляется при помощи взвешенного среднего. Таким образом, наибольший вес будет иметь тот вектор, значения которого ближе к известной части временного ряда, от которой строился прогноз. То есть при усреднении красный прогноз (на рисунке) будет иметь больший вес в левой части пропуска, а зеленый наоборот — в правой.
Получаем следующий результат:
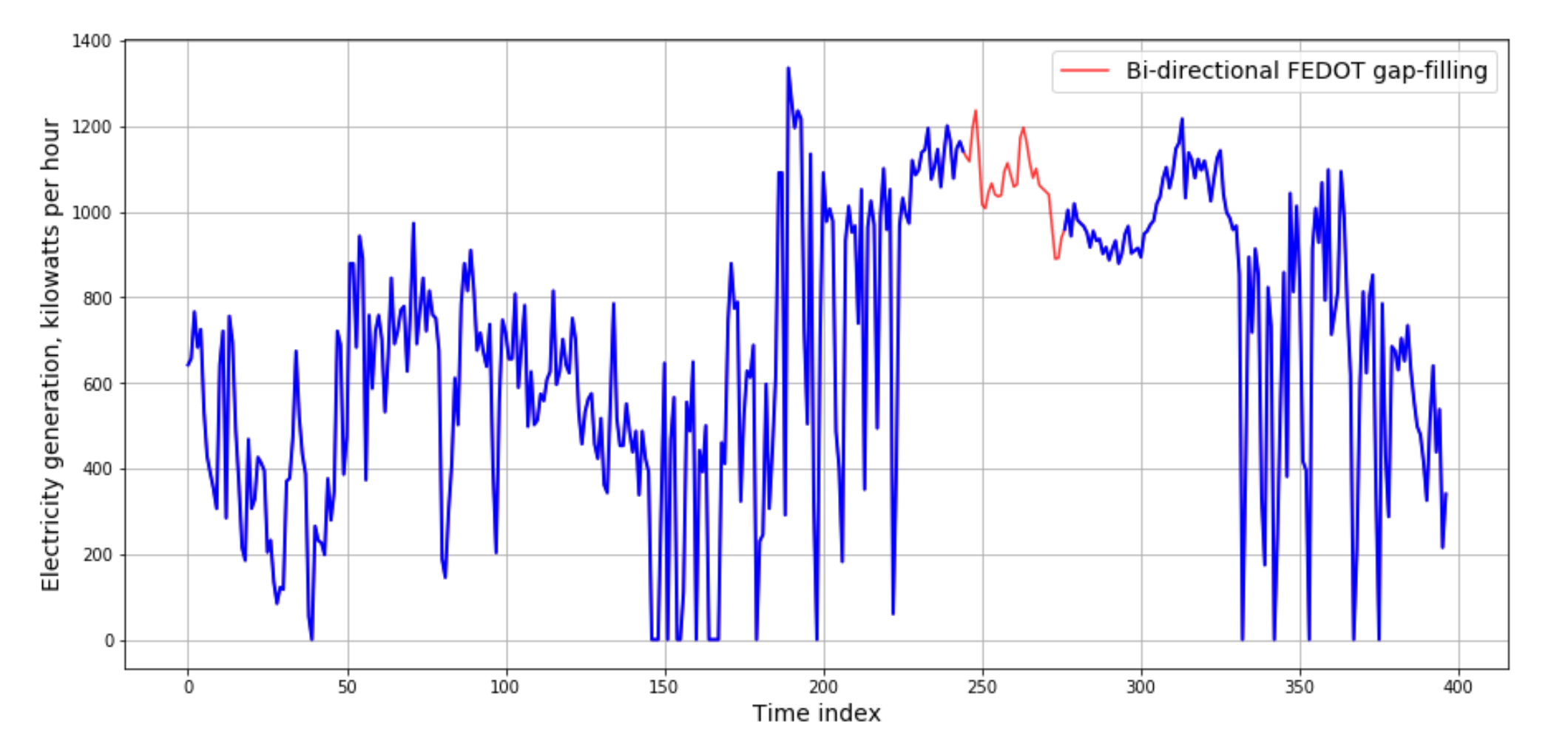
Заполненный пропуск во временном ряде выработки электроэнергии дизельным генератором
Неплохо! Но второй временной ряд еще имеет зияющую “дыру” посередине. Её мы можем восстановить так же как первую. Но мы поступим иначе. Сопоставим значения двух временных рядов в виде парной регрессии и восстановим значения выработки электроэнергии ветряком (отклик) с помощью ряда с дизельным генератором (предиктор). Эту задачу регрессии мы также будем решать при помощи FEDOT.
В результате получились восстановленные временные ряды, которые выглядят так:
Восстановленные временные ряды (видно, что они идут в противофазе — и заполненный пропуск не нарушает этот принцип)
Теперь оба временных ряда не имеют пропусков и готовы к использованию далее.
Построим цепочку для временных рядов при помощи AutoML. В FEDOT это можно сделать буквально в несколько строчек кода, используя API.
Коротко о том, что происходит “внутри”. AutoML работает в два этапа:
Настройка гиперпараметров по умолчанию осуществляется одновременно во всех узлах цепочки при помощи байесовских методов оптимизации:
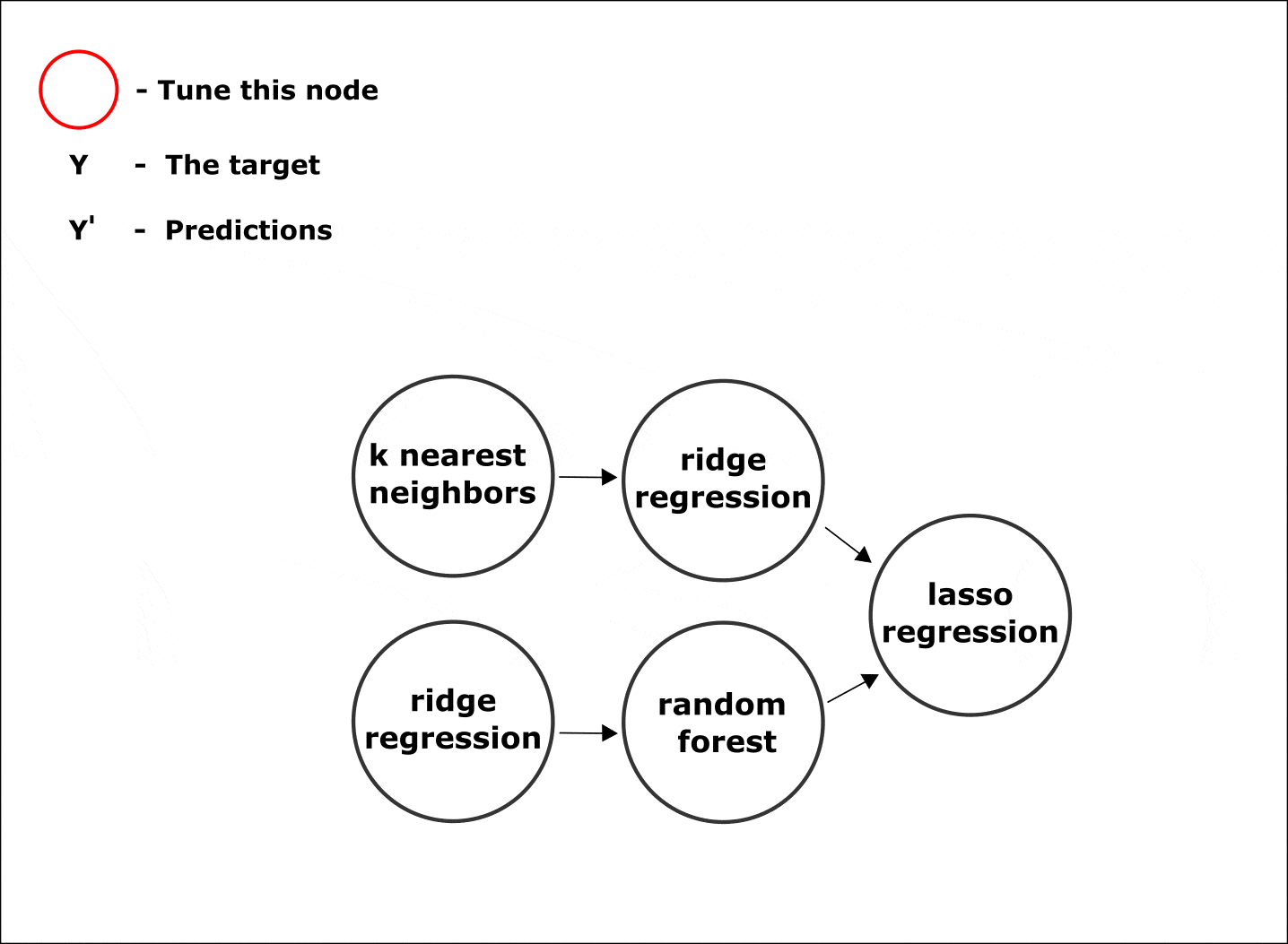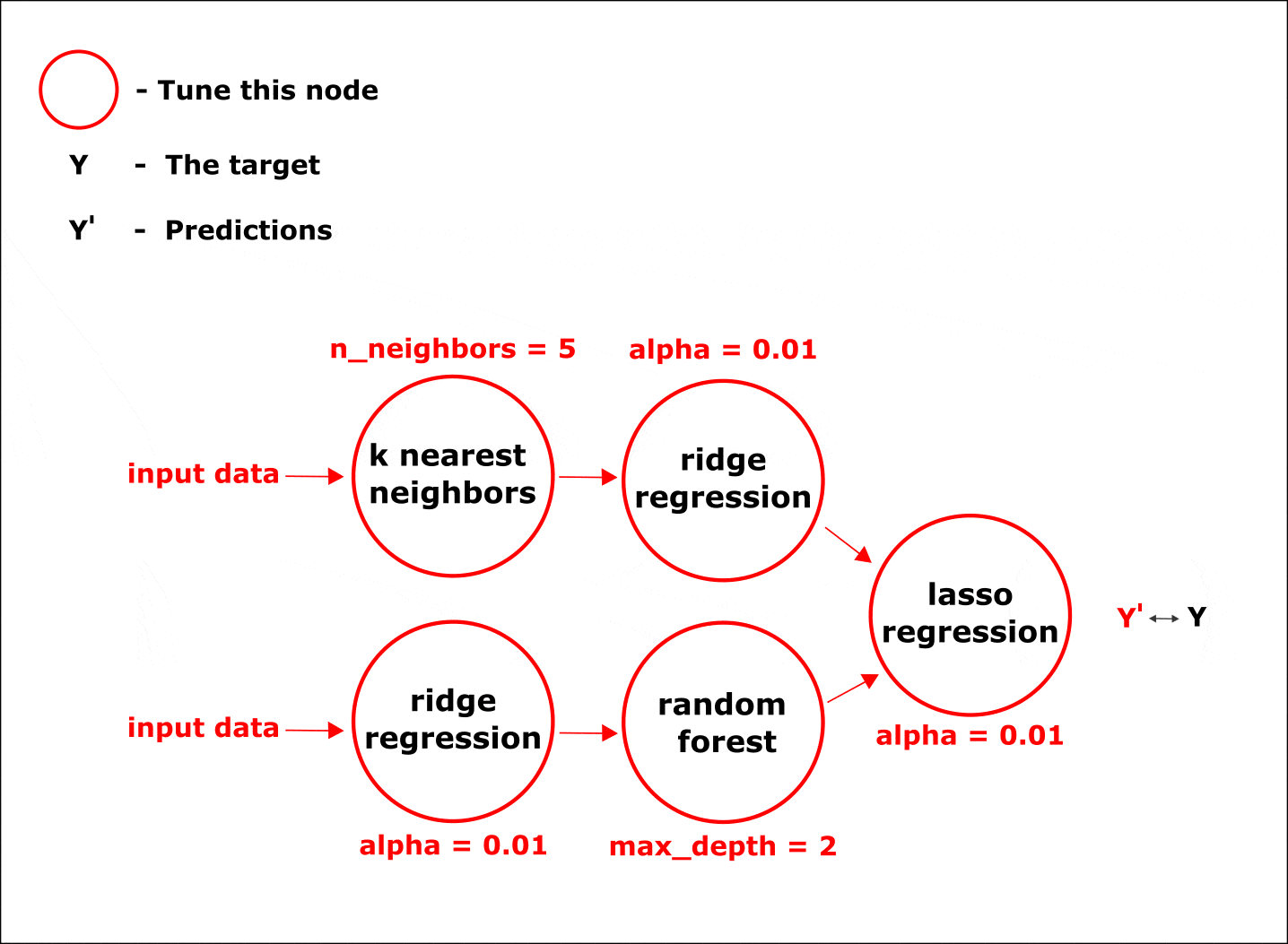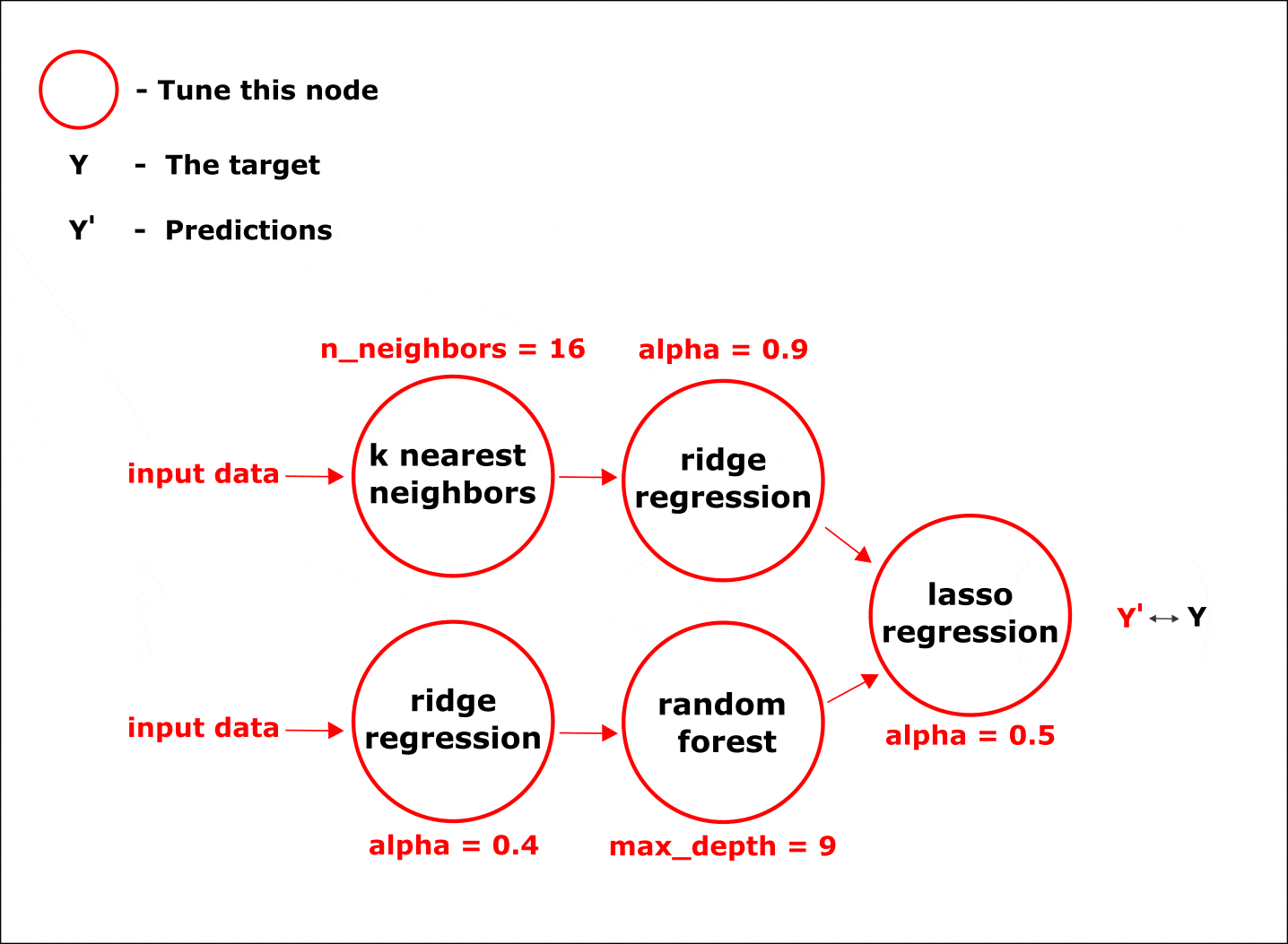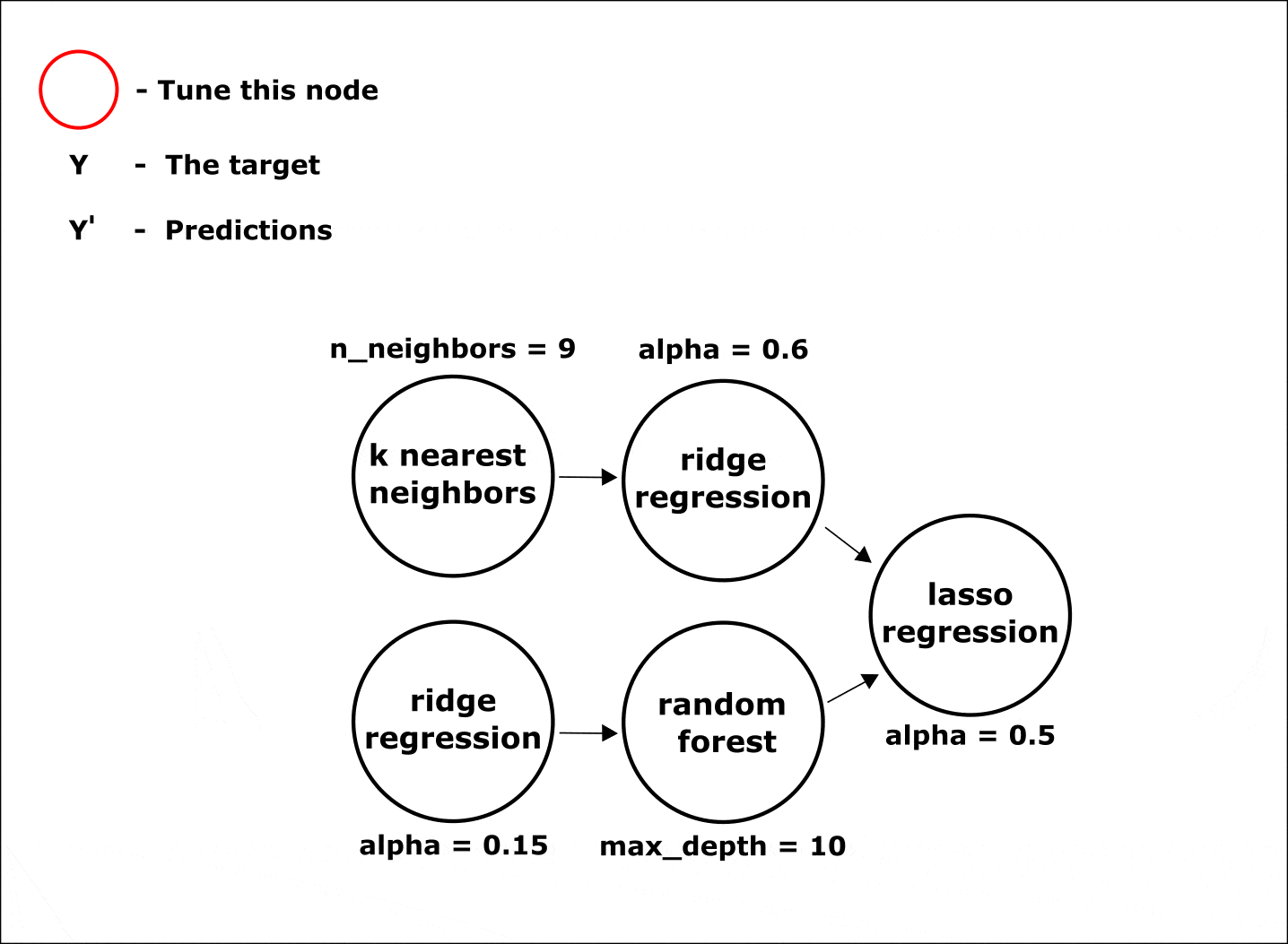
Анимация. Процесс настройки параметров в узлах композитной модели
После завершения всех этапов мы получаем итоговый пайплайн. Теперь посмотрим на получившийся прогноз и рассчитаем метрики: среднюю абсолютную ошибку (MAE) и корень из средней квадратической ошибки (RMSE): MAE — 100.52, а RMSE — 120.42.

Пример прогноза временного ряда
Если смотреть на график и значения метрик, возникает вопрос: хорошая ли получилась модель?
Ответ: определить трудно. На одном участке лучше модель не валидировать. Там ведь всего лишь 14 значений. Лучше посчитать метрику хотя бы три раза по 14 (то есть 42). Для этого стоит воспользоваться in-sample прогнозированием.
Ниже приведена анимация, которая должна помочь разобраться в out-of-sample и in-sample прогнозировании:
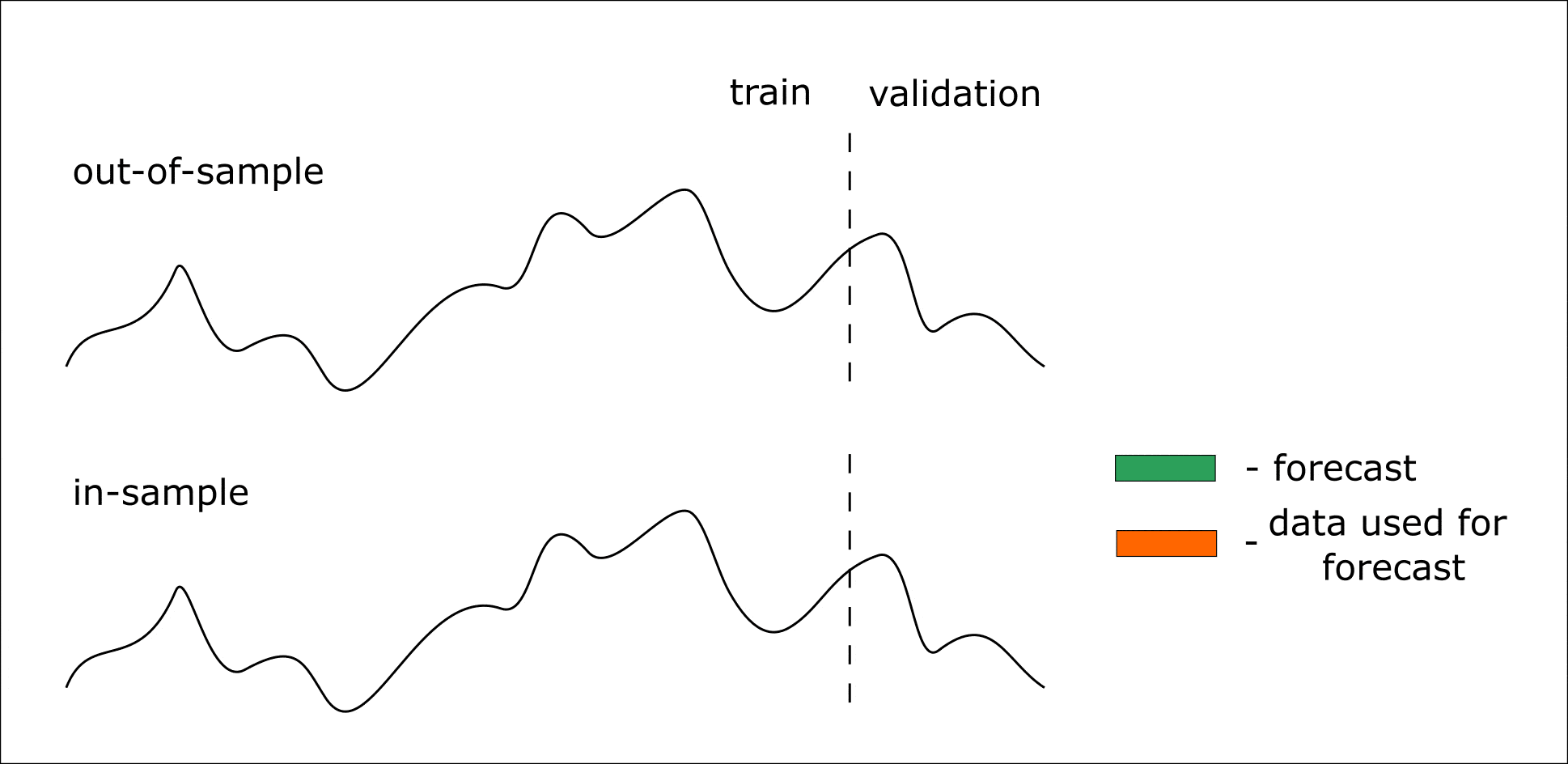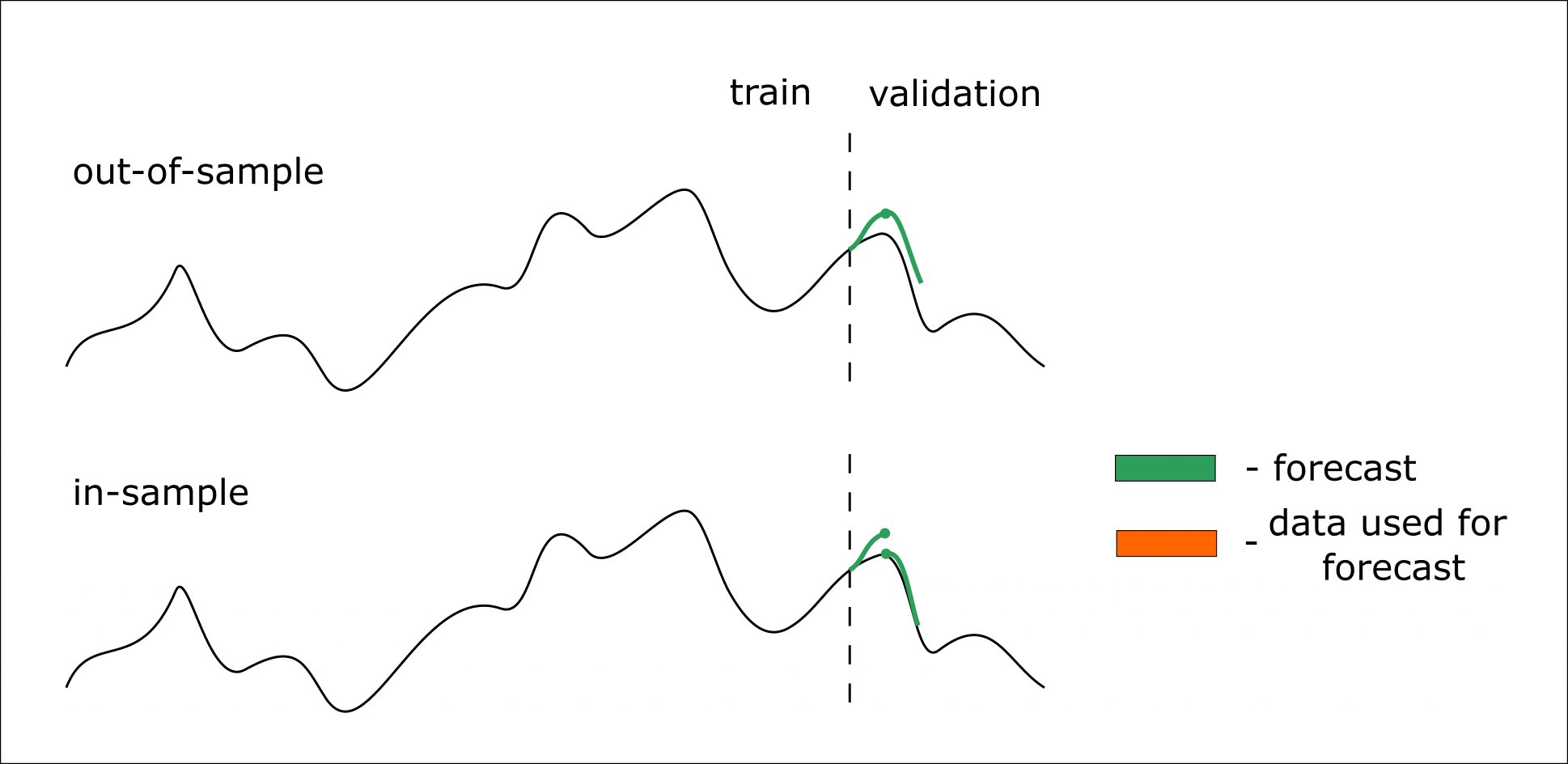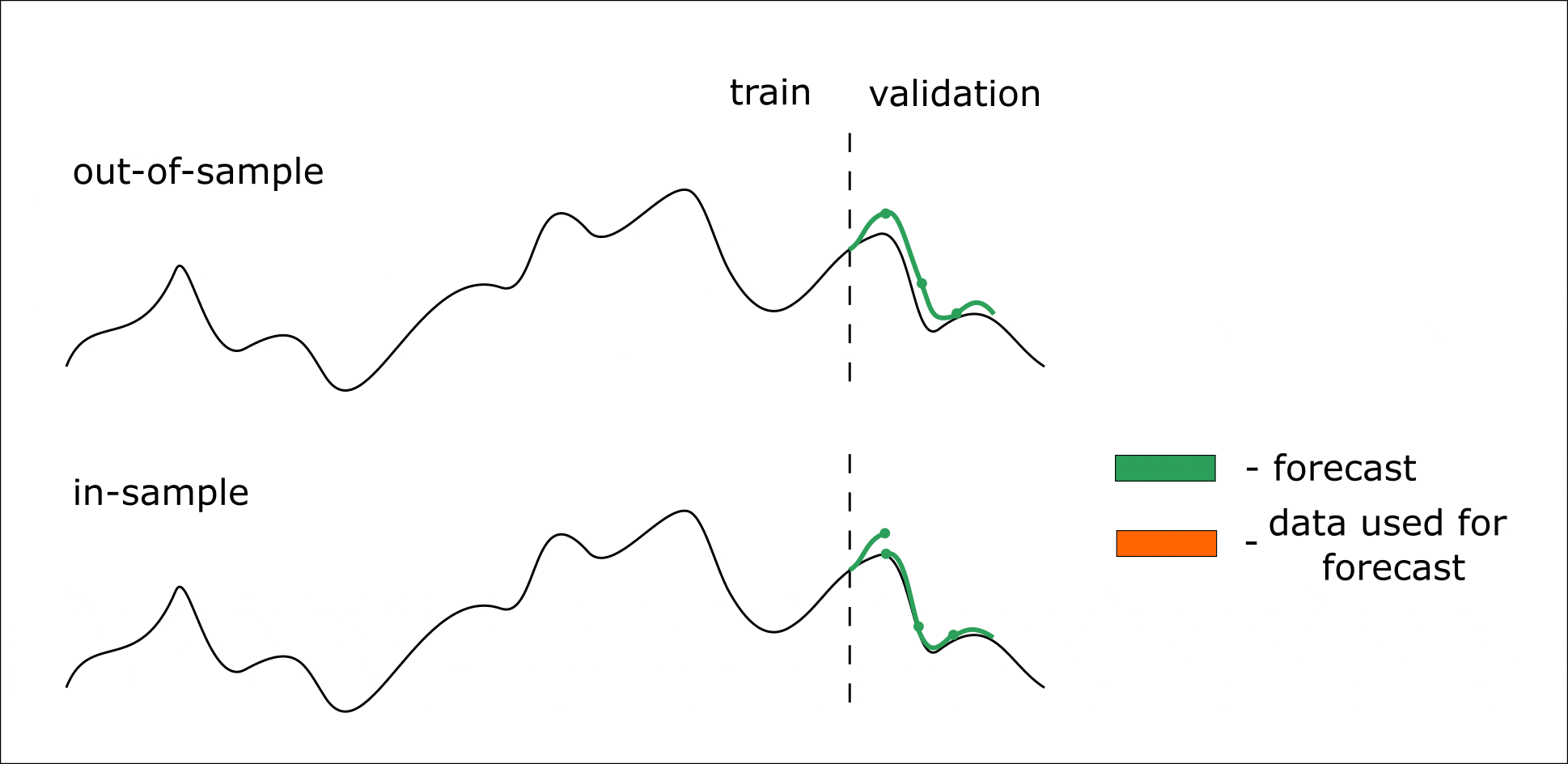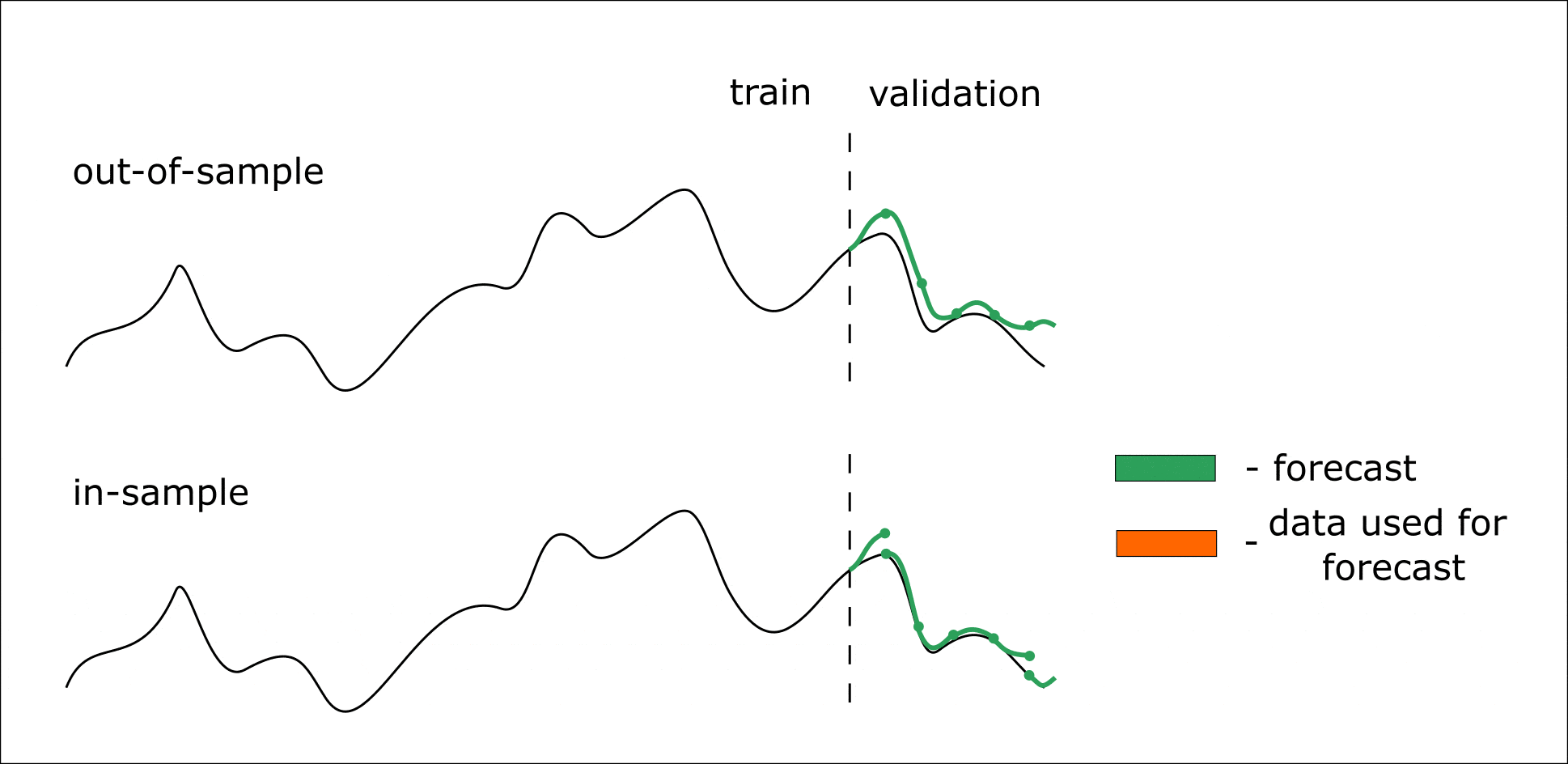
Анимация. Процесс in-sample и out-of-sample прогнозирования
Итак, мы наша модель умеет делать прогноз на 14 значений вперед. Но мы хотим получить прогноз на 28 значений вперед — в таком случае мы итеративно можем 2 раза сделать прогноз на 14 элементов. В таком случае в качестве предикторов для второго прогноза выступят значения, предсказанные на первой итерации (out-of-sample).
Если же мы хотим произвести валидацию модели, то воспользуемся in-sample прогнозированием. При таком подходе прогнозируем уже известную часть временного ряда (тестовая выборка). Но при итеративном прогнозировании для формирования предикторов на следующий шаг, используются не предсказанные значения на предыдущем шаге, а известные.
В FEDOT этот подход также реализован — так что теперь мы проверим алгоритм на 3-х блоках по 14 значений каждый. Для этого иначе разделим выборку и еще раз запустим композер. Результат прогнозирования отображен на рисунке ниже. Важно уточнить, что эволюционные алгоритмы имеют стохастическую природу, поэтому найденные решения могут отличаться.
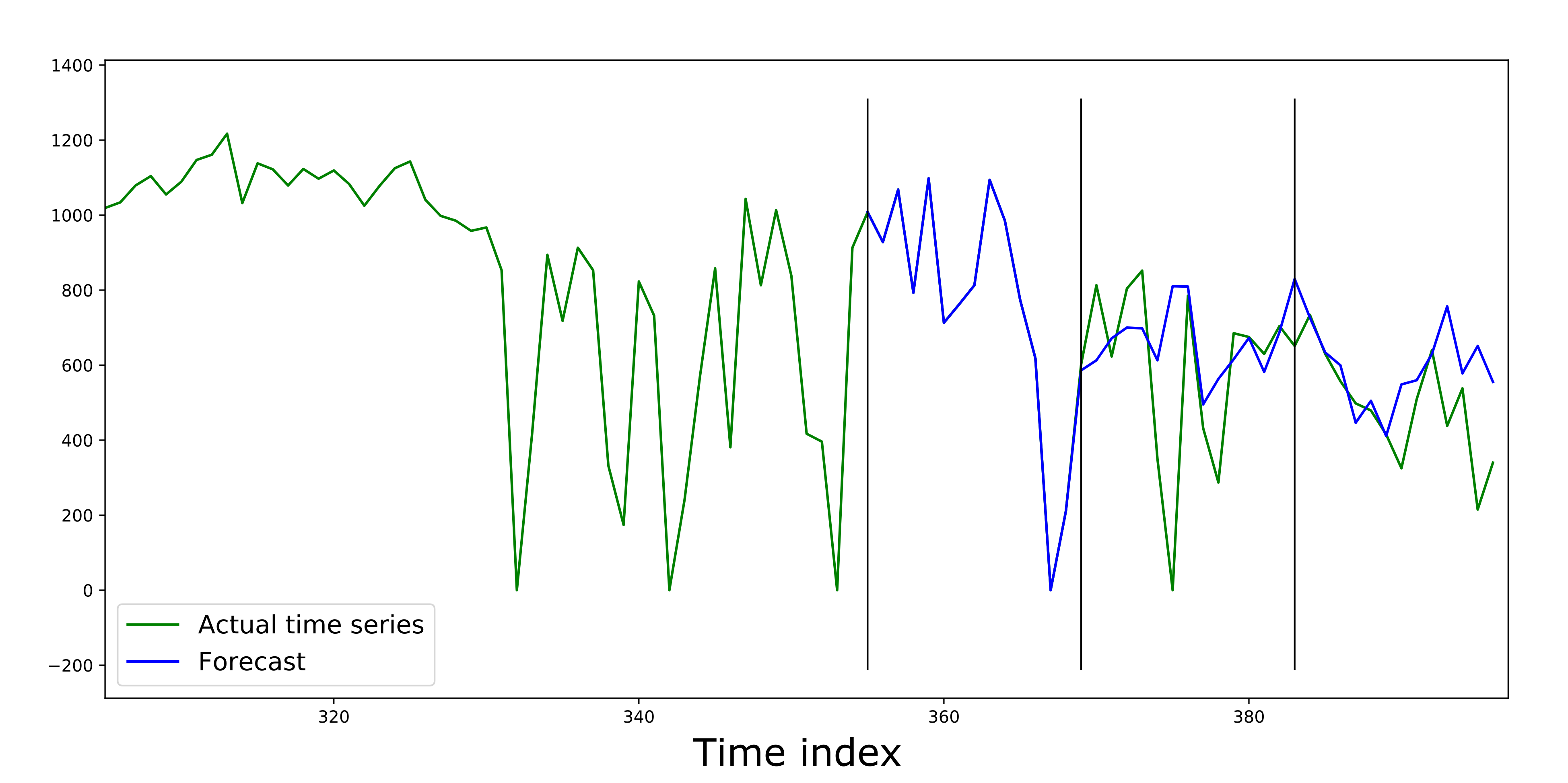
Валидация композитной модели для временного ряда на трех блоках по 14 элементов. Показана правая часть исходного временного ряда
Прогноз на первом валидационном блоке идеально повторил действительные значения временного ряда. Это кажется странным, но все проясняется, как только мы взглянем на структуру найденной цепочки.
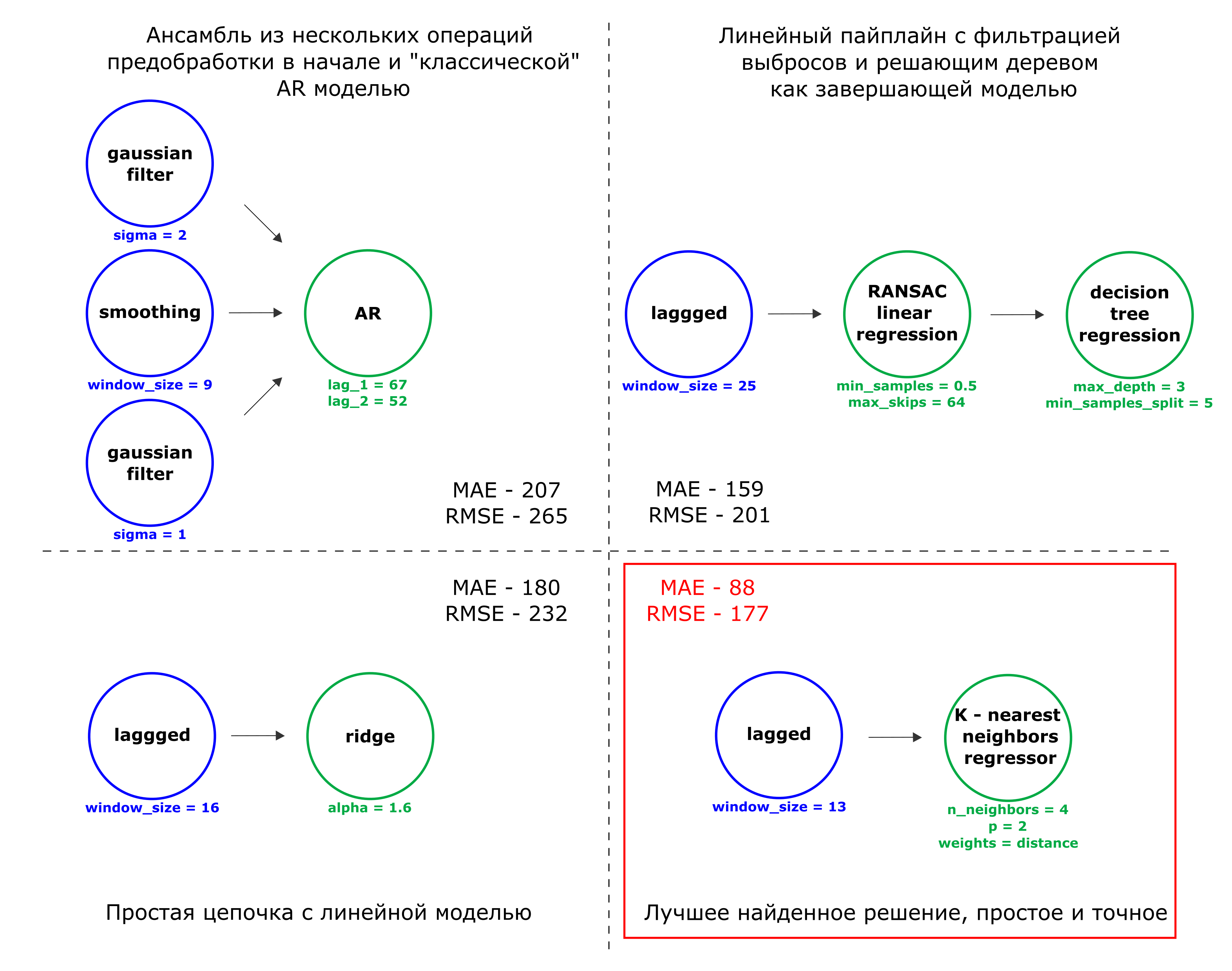
Примеры цепочек во время поиска решения (процесса эволюции). Рассматривались как пайплайны с множеством специфических для временных рядов операций предобработки, так и простые пайплайны, моделирующие линейные взаимосвязи
Как видно из рисунка, более сложные цепочки не всегда показывают высокую точность. Так, лучший найденный пайплайн получился короткий, но тем не менее, величина ошибки на валидации оказалась маленькой. Исходя из этого делаем вывод, что этого вполне достаточно для данного временного ряда.
Так как финальная модель — это алгоритм K-ближайших соседей, то цепочка хорошо умеет повторять паттерны временного ряда из обучающей выборки. Проблемы у такой модели могут возникнуть например для ряда, нестационарного по тренду. В таком случае модель K-ближайших соседей не сможет адекватно экстраполировать зависимости из обучающей выборки. У данного же временного ряда есть другая особенность — он нестационарен по дисперсии. Однако, в его структуре присутствуют относительно однородные части, которые немногим отличаются от того участка временного ряда, на котором производилась валидация.
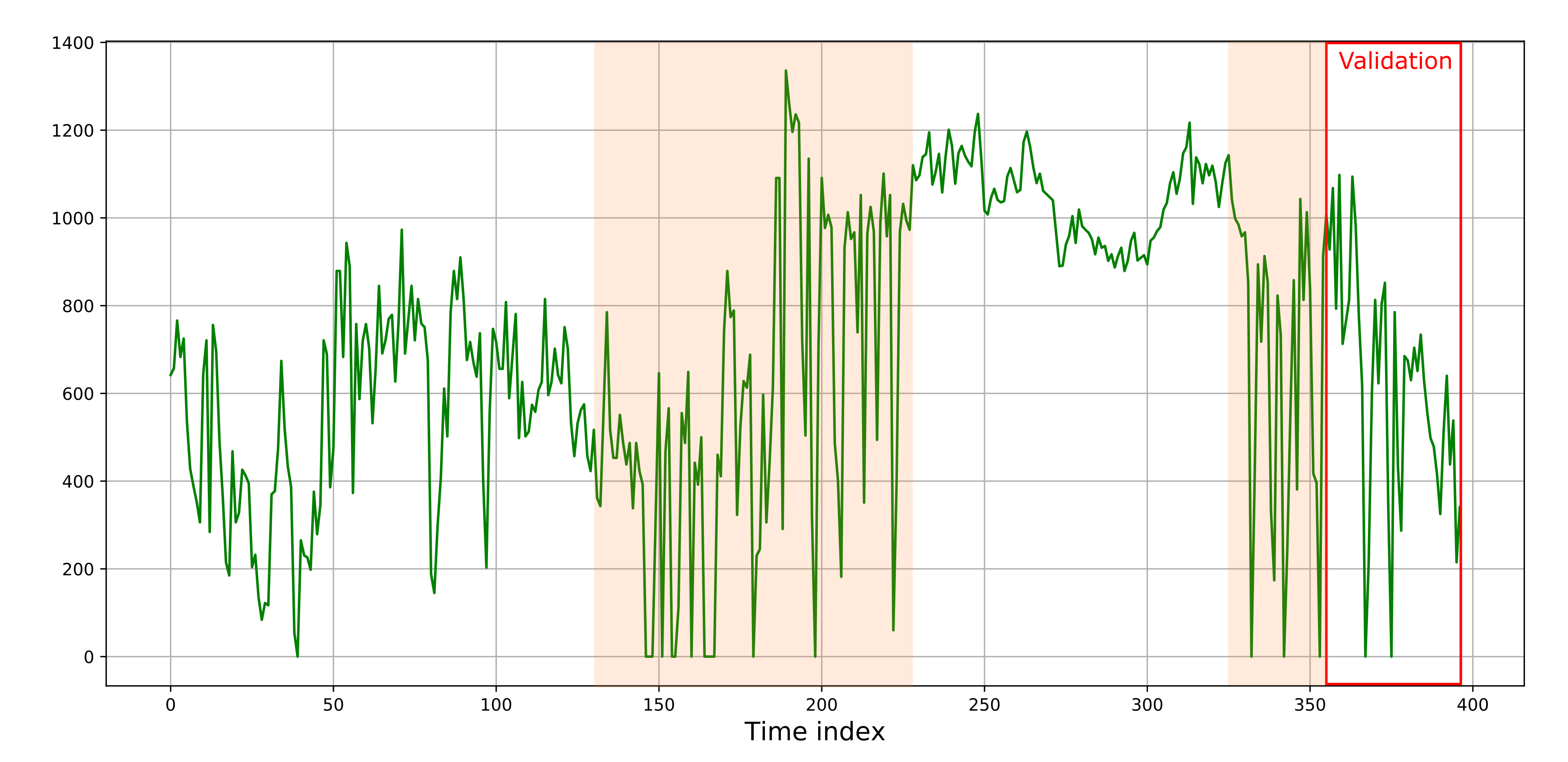
Однородные части временного ряда, “похожие” на валидационный участок, выделены оранжевым цветом
В этих частях присутствуют повторяющиеся паттерны, и при этом сам временной ряд не имеет тренда — величина колеблется вокруг среднего, то поднимаясь до значения выше 1000 кВт⋅ч, то опускаясь до 0. Поэтому умение воспроизводить эти паттерны для построенного пайплайна является очень важным. А вот угадывать низкочастотные колебания временного ряда (например, тренд или сезонность) при этом не обязательно. Модель K-nn как раз хорошо подходит для этих задач. Метрики качества прогнозирования, полученные после композирования цепочки, таковы: MAE — 88.19 и RMSE — 177.31.
Важно отметить, что мы получили готовое решение в автоматическом режиме и не вносили в алгоритм поиска каких-либо дополнительных экспертных знаний. Данная задача была решена всего за 5 минут работы фреймворка на десктопном ПК. Естественно, для больших наборов данных, потребуется больше времени на поиск решения.
Дисклеймер: Приведенное в этом разделе сравнение далеко не является исчерпывающим. По хорошему, для обоснования того, что один фреймворк лучше или хуже другого требуется проводить много больше экспериментов. Желательно использовать не один источник данных, применять кросс-валидацию, запускать алгоритмы на одних и тех же данных и с одними параметрами несколько раз (с последующим усреднением метрик). Здесь же мы привели ознакомительное сравнение: показали как с поставленной задачей могут справляться альтернативные решения. Если вас заинтересовало то, как FEDOT может справляться с временными рядами в сравнении с другими фреймворками, следите за новостями в нашем телеграмм канале. Полноценное сравнение в виде научной статьи скоро будет!
Попробуем также сравнить FEDOT с другими open-source фреймворками для прогнозирования временных рядов — AutoTS и pmdarima. Jupyter notebook с кодом, а также графиками, доступен по ссылке. Так как не во всех библиотеках реализована функциональность валидации на нескольких блоках, то решено было провести это небольшое сравнение на всего одном фрагменте ряда. Каждый алгоритм был запущен по 3 раза, и метрики ошибок были усреднены. Таблица с метриками выглядит следующим образом (в ячейках приведено СКО- среднее квадратическое отклонение):
| Библиотека | МАЕ∓СКО | RMSE∓CKO |
|---|---|---|
| pmdarima | 155∓1 | 196∓1 |
| AutoTS | 198∓22 | 236∓41 |
| FEDOT | 110∓14 | 170∓26 |
На рисунке также отображены прогнозы для одного из экспериментов:

Даже невооруженным взглядом видно, что в данной задаче прогноз от FEDOT больше “похож на правду”.
Итак, сегодня мы рассмотрели такую набирающую популярность область в машинном обучении, как AutoML. В статье мы попробовали показать, какие существуют решения на рынке для автоматической генерации ML-пайплайнов, и как их можно применять в задаче прогнозирования временных рядов.
Также мы попробовали AutoML на примере прогнозирования рядов вырабатываемой электроэнергии при помощи фреймворка FEDOT: восстановили пропущенные значения, построили композитную модель при помощи эволюционного алгоритма и произвели валидацию решения. В конце продемонстрировано краткое сравнение FEDOT с другими фреймворки на этой задаче.
Примеры (код и картинки) из данного поста доступны в отдельном репозитории по ссылке.
Пара дополнительных ссылок для тех кто решил покопать поглубже:
Используйте AutoML, пробуйте FEDOT!
Над статьей работали: Михаил Сарафанов, Павел Вычужанин и Николай Никитин.