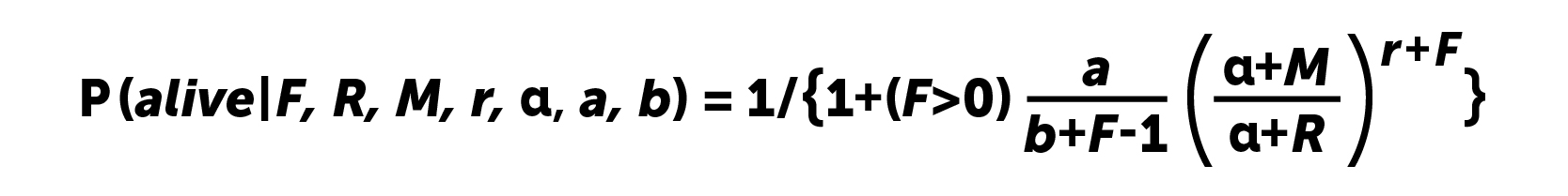https://habr.com/company/plarium/blog/431520/- Блог компании Plarium
- Data Mining
- Python
- Машинное обучение
- Разработка игр
Представьте: телефонный звонок в три часа ночи, вы берете трубку и слышите крик о том, что больше никто не пользуется вашим продуктом. Страшно? В жизни, конечно, все не так, но если не уделять должное внимание проблеме оттока пользователей, можно оказаться в похожей ситуации.
Мы уже подробно
рассказали, что такое отток: углубились в теорию и показали, как превратить нейросеть в цифрового оракула. Специалисты студии Plarium Krasnodar знают еще один способ предсказания. О нем мы и поговорим.

Это не тот RFM, что нам нужен
RFM — это метод, который используется для сегментации клиентов и анализа их поведения. На основе полученных данных можно создать программу лояльности для каждой группы, построить распределение пользователей и спрогнозировать, когда они вернутся за покупками.
История разработки RFM началась в 1987 году, когда была опубликована статья
Counting Your Customers: Who Are They and What Will They Do Next. В ней описывался метод анализа, основанный на распределении Парето (двухпараметрическое семейство абсолютно непрерывных распределений).
Модель называлась Pareto/NBD и учитывала лишь историю покупок пользователей. В классической трактовке работа этого метода строилась на пяти столпах, или приближениях:
- Пока пользователи активны, количество транзакций, сделанных покупателем в течение периода t, подчиняется распределению Pareto со средним λt.
- Неоднородность параметра λ (transaction rate) следует гамма-распределению с параметрами r и α.
- Каждый покупатель имеет необозримый промежуток времени «жизни» τ. Точка, в которой пользователь становится неактивным, распределена экспоненциально с параметром μ (dropout rate).
- Неоднородность параметра μ среди пользователей следует гамма-распределению с параметрами s (shape) и β (scale).
- Параметры λ и μ могут независимо изменяться среди покупателей.
Недостатками такой модели были как высокая сложность вычисления гипергеометрических функций Гаусса, так и поиск максимума функции правдоподобия.
В статье 2003 года
«Counting Your Customers» the Easy Way: An Alternative to the Pareto/NBD Model была опубликована идея реализации более совершенной модели. Помимо истории покупок, в ней использовались еще два параметра: частота и давность. Главным ее отличием от Pareto/NBD было то, как определяется момент ухода покупателя.
В классической постановке предполагалось, что пользователь способен уйти в любое время, независимо от частоты и рисунка его покупок в прошлом. Новый подход основан на гипотезе, что покупатель может начать терять интерес сразу после завершения сделки.
Это упростило вычисления и привело к модели beta-geometric (BG/NBD). В ней используются три основных параметра: recency, frequency, monetary, — а также четыре дополнительных: r, α, a, b (параметры a и b добавились из
бета-распределения).
RFM помогает предсказать, совершит ли клиент покупку в будущем. Специалисты Plarium Krasnodar модифицировали этот метод.
Предсказываем отток просто и со вкусом
Для расчетов нам понадобится массив данных об игровых сессиях. Он пересчитывается в матрицу, состоящую из параметров R-F-M, и еще в четыре коэффициента, которые выбираются моделью в процессе обучения.
В контексте игры параметры приобретают следующие значения:
- Recency — как долго пользователь играл в момент последнего входа;
- Frequency — как часто пользователь повторно заходил в игру;
- Monetary — как долго пользователь играет (время «жизни»).
Параметры агрегируются в матрицу. Затем она загружается в модель, которая рассчитывает вероятность «жизни» пользователей — шанс того, что они продолжат играть.
Вычисления производятся по формуле:
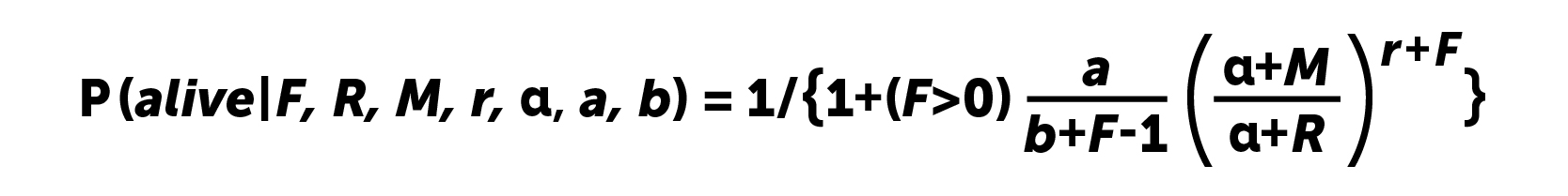
Очевидно, что для пользователей без повторных входов вероятность «жизни» будет равна единице. В 2008 году авторы статьи
Computing P(alive) Using the BG/NBD Model предложили решение этой проблемы. Игровые компании могут использовать два варианта, которые дают похожие результаты.
Метод 1 — для всех пользователей вводится параметр π. Он показывает, какие игроки считаются неактивными.
Метод 2 — добавляется единица к параметру Frequency. Эта мера позволяет избежать вырождения формулы при Frequency = 0, но искусственно добавляет еще один вход в игру для каждого пользователя.
Как адаптировать метод RFM для геймдева
Предположим, что у нас есть новый пользователь. Он только что вошел в игру. Параметр
F = 1 (либо 0, в зависимости от расчетов), так как первый вход не считается, а повторных у игрока еще не было.
Пользователь играет три дня. Параметры меняются:
F учитывает только ежедневные входы, поэтому его значение равно 2, а показатели
М и
R равны 3. Используя эти данные, мы получаем вероятность «жизни», приближенную к единице.
На следующий день пользователь не заходит в игру. Параметр
М обновляется, а
F и
R остаются прежними. Подставляя все значения в формулу, мы видим, что показатель вероятности стал ниже.
Если в течение недели пользователь не играет, то показатель
М вновь обновляется и вероятность «жизни» падает еще больше.
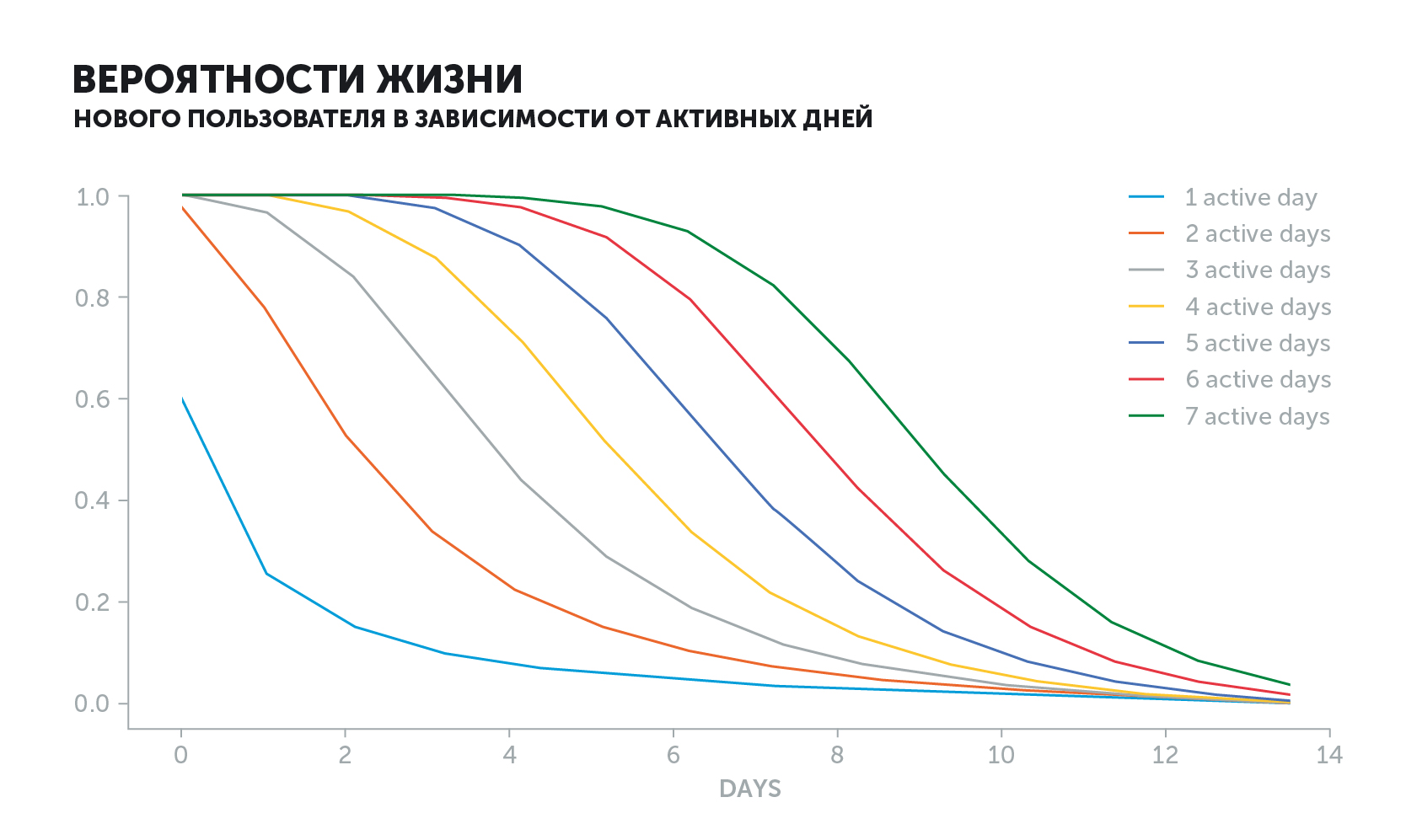
График активного пользователя выглядит иначе. Вероятность «жизни» будет уменьшаться в зависимости от его истории. Если он ежедневно заходил в игру и внезапно перестал, то значение показателя упадет намного быстрее, чем если бы он играл раз в два дня.

Весомые плюсы и неочевидные минусы RFM
Главное достоинство этого метода — простота:
- для расчетов не нужно использовать сложный математический аппарат;
- показатели рассчитываются по относительно простой формуле;
- можно обойтись без сложных пайплайнов для данных;
- все оптимальные параметры модели подбираются автоматически.
Помимо этого, данные RFM легко интерпретировать. Изучая историю пользователя, можно понять, почему у него такая вероятность «жизни». Часто при работе с более сложными методами труднее сделать конкретные выводы.
Минусы у RFM тоже есть.
Во-первых, это не самый точный метод. Он работает хорошо, но при расчетах не используется ряд параметров. Например, многие пользователи, начинающие терять интерес, по привычке заходят в игру. То есть среднее количество игровых сессий в сутки падает, а частота повторных входов не изменяется.
Во-вторых, метод не учитывает активность пользователя: сколько ресурсов он передал, атаковал ли противника, создал ли войска. Если мы возьмем всех игроков с вероятностью «жизни» равной ~0,8, то в зависимости от параметров и их истории кроме активных будут и те, которые заходят раз в три дня.
В-третьих, ушедший пользователь становится «живым», когда снова запускает игру. При чем он может сделать это спустя месяц с момента последнего входа. Такие ситуации усложняют детекцию игроков с большими паузами между сессиями. В целом это не критично, хотя и вносит определенный дисбаланс, когда мы пытаемся понять, «жив» пользователь или нет.
Не лучше ли использовать нейросеть?
Лучше, но в первую очередь нужно понять, как реализовать проект: решать масштабные задачи с наскока или постепенно двигаться к цели.
RFM-анализ показывает вероятность «жизни» пользователя в момент, когда производится расчет. Мы не сможем понять, уйдет игрок через две или три недели, а нейросеть сможет. Учитывая всю инфраструктуру, создать такую комплексную систему для анализа поведения игроков с нуля гораздо сложнее. Более того, необходима baseline, с которой можно сравнить качество работы нейронной сети. Подобный подход, скорее всего, обернется финансовыми потерями, если не рассчитать силы.
Наш опыт показывает, что глобальные задачи нужно реализовывать постепенно. Создать рабочий прототип несложно, а вот собрать и обработать данные, настроить и обучить нейросеть — другое дело. Эти процессы могут растянуться на долгое время, которого всегда не хватает.
Именно поэтому мы решили сначала воспользоваться более простой моделью: провели исследования, выявили плюсы и минусы, опробовали ее в работе. Результаты нас устроили. У RFM есть недостатки, но они щедро компенсируются простотой использования. А нейронная сеть — следующий шаг к улучшению системы.