news.shamcode.ru | Похоже, я придумал свой алгоритм поиска кратчайшего пути (upd_1: увы, но нет. upd

Всем привет! Я реализовал, похоже, собственный алгоритм поиска кратчайшего пути с отрицательными ребрами графа.

Почему собственный? Я искал подобное решение, но не нашел, возможно, оно уже было реализовано, просто плохо поискал. Жду Нобелевскую премию =)

Додумался я до него путем модификации классического Дейкстры. Прошу адекватно отнестись к содержимому, ибо это моя первая статья, и, возможно, я ничего не придумывал и, вообще, этот алгоритм не работает вовсе (но по моим тестам он работает правильно).

Повторюсь, алгоритм работает с отрицательными ребрами графа (но не с циклическими отрицательными). Чем этот алгоритм отличается от известного Беллмана-Форда?

Сложностью! У известного алгоритма сложность составляет O(n³). У "моего" алгоритма по моим расчетам сложность не превышает оригинальной сложности алгоритма Дейкстры, а именно O(n²). Если это не так, поправьте, пожалуйста, после ознакомления с реализацией на языке Python

Реализация

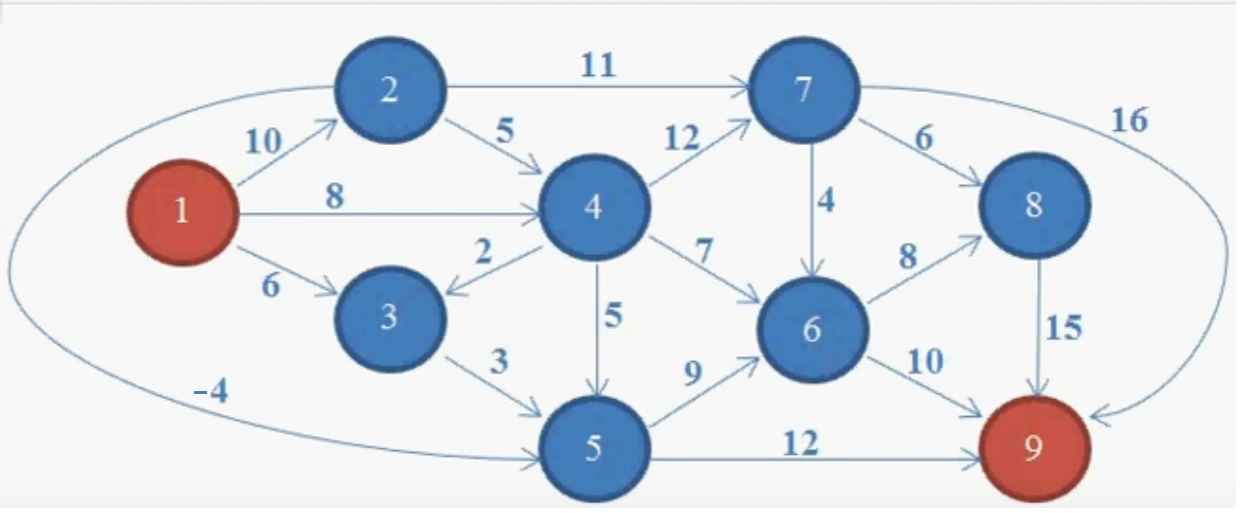
Итак, у нас есть граф с отрицательным ребром между 2-м и 5-м узлом. Наша задача - найти кратчайший путь от источника (1-го узла) до 9-го узла.

Граф будет храниться в виде хэш таблицы, где:

graph = {
нода_1_(источник): {сосед_1: вес до него, сосед_2: вес до него, ...},
нода_2: {сосед_1: вес до него, сосед_2: вес до него, ...},
...
}

graph = {
    1: {2: 10, 3: 6, 4: 8},
    2: {7: 11, 4: 5, 5: -4},
    3: {5: 3},
    4: {7: 12, 3: 2, 5: 5, 6: 7},
    5: {6: 9, 9: 12},
    6: {8: 8, 9: 10},
    7: {6: 4, 8: 6, 9: 16},
    8: {9: 15},
    9: {}
}

Важно! Нужно писать узлы графа в порядке их отдаленности от источника. Т.е. сперва описываем первых соседей источника. После того, как описали их, приступаем к следующим соседям соседей. Т.е. описываем поуровнево, будто это не взвешенный граф, а обыкновенное дерево, где реализовываем поиск в ширину. В Python словари являются упорядоченными (начиная с версии 3.6), поэтому нам не стоит прибегать к другим структурам данных, типа Ordered dict из модуля collections.
Можно описать граф матрицей смежностей, но мне так проще.

P.S. Тот, кто задается подобным вопросом:

Определение графа знаете? Набор вершин и дуг, в котором дуги являются парами связных вершин, плюсом веса для дуг в нашем случаи. Никакого порядка там в принципе не предусмотрено.

Заранее отвечаю.

Хорошо, буду от вашей структуры отталкиваться. У нас какая задача? Найти кратчайший путь из точки А в точку В. Находим в вашем представлении графа точку А и смотрим на его соседей. Потом находим этих соседей и смотрим их соседей и т.д. Вот это "находим" в вашей беспорядочной структуре будет за N выполняться N раз. Это будет в том случае, если ноды у вас просто беспорядочно расположены в массиве (если вы используете эту структуру данных для хранения). Обычно в программе номер ноды совпадает с номером ячейки в массиве, что позволяет получить к этой ноде доступ за константу. В алгоритме Дейкстры (не я придумал его) как раз таки задача решается именно таким представлением графа, где номер ноды (или буква в лексиграфическом порядке) совпадает с номером ячейки в массиве. То, как вы пытаетесь представить граф - это по сути выстрел себе в ногу. Если отталкиваться от реальной жизни, нужно еще реализовать построение такой структуры графа. Условно ты находишься на перекрестке 1, мне надо в перекресток 10. А дай ка гляну, какие там дороги исходят из перекрестка 7 и запишу. Хотя можно было на второе место записать дороги перекрестка 2. В общем, замечание ваше понятно, но это всё общепринятая условность представления данных графа, я это не придумывал.
Поиск в ширину же выполнится за линейное время, поэтому он никак не увеличивает сложность алгоритма.

Так же нам понадобится еще 2 хэш таблицы.
Минимальные веса от источника до этой ноды в виде:
costs = {
нода_1_(источник): 0,
нода_2: infinity,
нода_3: infinity,
...
}
Заполнять и обновлять мы ее будем по мере прохождения по "детям" узлов.

costs = {}  # Минимальный вес для перехода к этой ноде (кратчайшие длины пути до ноды от начального узла)

Таблица родителей нод, от которых проходит кратчайший путь до этой ноды:

parents = {}  # {Нода: его родитель}

Ее так же будем заполнять и обновлять по мере прохождения по детям узлов.

Как и в алгоритме Дейкстры, будем отмечать еще неизвестные до узлов расстояния бесконечностью. Инициализируем эту переменную:

infinity = float('inf')  # Бесконечность (когда минимальный вес до ноды еще неизвестен)

Далее создаем пустое множество. Там будут храниться обработанные узлы (что значит "обработанные", поясню далее, а пока просто создаем множество)

processed = set()  # Множество обработанных нод

Приступим к самому алгоритму!

Начинаем с источника (первого узла). Смотрим на веса всех его соседей в таблице costs. Путь до них бесконечный, а любое число уже меньше бесконечности, поэтому обновляем веса. Так же вносим родителей всех узлов, т.к. мы обнаружили путь до ноды короче. Когда посмотрели всех соседей, вносим наш рассматриваемый узел в множество обработанных узлов processed (этот узел мы не будем обрабатывать в дальнейшем).
Здесь важный момент и отличие от алгоритма Дейкстры. Мы будем смотреть не минимальный по весу необработанный узел, а смотреть вообще ВСЕХ соседей поочередно. Т.е. у нас есть соседи после первого этапа алгоритма.
Мы поочередно так же будем искать уже их соседей и обновлять минимальные веса. Если же достижимый вес окажется меньше, чем внесенный в таблицу, то мы его заменяем. Так же заменяем его родителя в таблице parents.
Когда посмотрели всех соседей, вносим узел в множество обработанных. Т.е. множество обработанных - это те узлы, у которых мы рассмотрели всех его соседей!
И так повторяем поуровнево (не приступаем к соседям соседей, пока не обработаем первых соседей), пока не будут обработаны все узлы.
Код:

graph = {
    1: {2: 10, 3: 6, 4: 8},
    2: {7: 11, 4: 5, 5: -4},
    3: {5: 3},
    4: {7: 12, 3: 2, 5: 5, 6: 7},
    5: {6: 9, 9: 12},
    6: {8: 8, 9: 10},
    7: {6: 4, 8: 6, 9: 16},
    8: {9: 15},
    9: {}
}

parents = {}  # {Нода: его родитель}
costs = {}  # Минимальный вес для перехода к этой ноде (кратчайшие длины пути до ноды от начального узла)
infinity = float('inf')  # Бесконечность (когда минимальный вес до ноды еще неизвестен)

processed = set()  # Множество обработанных нод
for node in graph.keys():
    if node not in processed:  # Если нода уже обработана не будем ее заново смотреть (иначе м.б. беск. цикл)
        for child, cost in graph[node].items():  # Проходимся по всем детям
            new_cost = cost + costs.get(node,
                                        0)  # Путь до ребенка = путь родителя + вес до ребенка (если родителя нет, то путь до него = 0)
            min_cost = costs.get(child,
                                 infinity)  # Смотрим на минимальный путь до ребенка (если его до этого не было, то он беск.)
            if new_cost < min_cost:  # Если новый путь будет меньше минимального пути до этого,
                costs[child] = new_cost  # то заменяем минимальный путь на вычисленный
                parents[child] = node  # Так же заменяем родителя, от которого достигается мин путь
        processed.add(node)  # Когда все дети (ребра графа) обработаны, вносим ноду в множество обработанных

print(f'Минимальные стоимости от источника до ноды: {costs}')
print(f'Родители нод, от которых исходит кратчайший путь до этой ноды: {parents}')

# -> Минимальные стоимости от источника до ноды: {2: 10, 3: 6, 4: 8, 7: 20, 5: 6, 6: 15, 9: 18, 8: 23}
# -> Родители нод, от которых исходит кратчайший путь до этой ноды: {2: 1, 3: 1, 4: 1, 7: 4, 5: 2, 6: 4, 9: 5, 8: 6}

Мы получили кратчайшие расстояния от источника до каждого достижимого узла в графе, а так же родителей этих узлов. Как же нам построить цепочку интересующего нас пути от источника до 9-ой ноды (либо до любой другой достижимой)? Ответ в коде ниже:

def get_shortest_path(start, end):
    '''
    Проходится по родителям, начиная с конечного пути,
    т.е. ищет родителя конечного пути, потом родителя родителя и т.д. пока не дойдет до начального пути.
    Тем самым мы строим обратную цепочку нод, которую мы инвертируем в конце, чтобы получить
    истинный кратчайший путь
    '''
    parent = parents[end]
    result = [end]
    while parent != start:
        result.append(parent)
        parent = parents[parent]
    result.append(start)
    result.reverse()
    shortest_distance = 0
    for i in range(len(result)-1):  # Узнаем кратчайшее расстояние
        node_1 = result[i]
        node_2 = result[i + 1]
        shortest_distance += graph[node_1][node_2]
    result = map(str, result)  # В случае если имена нод будут числами, а не строками (для дальнейшего join)
    print(f'Кратчайший путь от {start} до {end}:  {shortest_distance}')
    return result


shortest_path = get_shortest_path(start=1, end=9)
print('-->'.join(shortest_path))

# -> Кратчайший путь от 1 до 9:  18
# -> 1-->2-->5-->9

Итак, мы нашли кратчайший путь до 9 узла, и обратите внимание, он проходит через ребро с отрицательным весом! Т.е. нас теперь не пугает наличие такого ребра, в отличие от оригинальной Дейкстры.

Сложность

В оригинальном алгоритме Дейкстры сложность в худшем случае складывается из

Прохода по всем узлам графа (n)
В этот цикл вложен еще один - поиск минимального не посещенного узла. Он работает за O(n), но можно сделать и за O(Elogn) путем реализации кучи (heapq)
Прохождение по соседям узла. Занимает O(E), где Е - количество ребер в графе. Т.к. это константа, то ее опускают.

Итого алгоритм занимает O(n²+E), а с реализацией кучи, скорость возрастает до O(Elogn) (на самом деле это будет не всегда так, но в большинстве случаев)

Что касается "моего" алгоритма, то если где-то не ошибаюсь:

Проход по всем узлам графа O(n)
Проход по всем соседям O(n)
Обновление весов O(1)

Итого O(n²). Not bad! Что по памяти? costs - O(n), parents - O(n), processed - O(n)
Считаю, неплохо для такого рода алгоритма.

Еще деталь такая. При реализации классической Дейкстры, в случае, когда поиск МИНИМАЛЬНОГО по весу узла совпадет с нашим конечным целевым узлом,
то мы можем прервать дальнейшую обработку, т.к. мы уже нашли кратчайший путь до интересующего узла. В "моем" же алгоритме мы все равно будем обрабатывать все узлы.

Выводы

В случае, если нам могут встретится отрицательные ребра в графе, можно пользоваться данным алгоритмом. Можно воспользоваться и известным Беллмана-Форда, кому как нравится, но мне показался он более сложным в понимании.
В случае, если нам известно, что граф не содержит отрицательных весов, тогда можно смело пользоваться Дейкстрой.

ЕЩЕ РАЗ ПОДЧЕРКИВАЮ!

Я не знаю, был ли этот алгоритм до этого или нет. Может он вообще работает некорректно, но я тестировал его с разными данными, и он работал правильно.

Если будут какие-то поправки или замечания, жду обратную связь. Может быть, реализация вообще работает только с определенными графами, возможно, есть и такие, которые все сломают :)

Всем спасибо, жду Ваше мнение по поводу этой статьи!

Update_1:

Все-таки алгоритм не работает с определенными графами :(

Приведу пример, подсказанный с комментариев (спасибо большое за него):

Хотим попасть с источника 1 до конечной ноды 5.

graph = {    
    1: {2: 1, 3: 20, 5: 10},
    2: {4: 1},
    3: {5: 1},
    5: {},
    4: {3: 1},
}

# OUT
"""
Минимальные стоимости от источника до ноды: {2: 1, 3: 3, 5: 10, 4: 2}
Родители нод, от которых исходит кратчайший путь до этой ноды: {2: 1, 3: 4, 5: 1, 4: 2}
Кратчайший путь от 1 до 5:  10
1-->5
"""
# Правильный ответ - 4
# 1-->2-->4-->3-->5

Происходит это, потому что мы обновляем веса уже обработанных нод, но не обновляем в свою очередь их соседей (по идее веса соседей с учетом обновления веса родителя могут быть короче).

Чтобы все работало, нужно заново обрабатывать этого родителя, что в свою очередь приводит к росту сложности. Я даже уже не знаю, в какую, по-моему кубическую, что по сути уже бесполезно использовать, т.к. есть уже известный алгоритм Беллмана-Форда с такой же ассимптотикой. Возможно, можно как-то и оптимизировать хитрым способом, но пока в голову ничего не пришло. Если есть какие-то мысли по этому поводу, какие-то идеи - welcome! Присылайте идеи в комментариях.

Всем спасибо за помощь и фидбэк! Я добился своей цели - ответил себе на вопрос, корректный ли алгоритм или нет. Спасибо людям за это, я получил опыт и закрепил знания, а это уже победа!

Update_2:

Ситуация немного изменилась. Как мне объяснили в комментариях более подготовленные люди, сложность алгоритма была не O(n²), а O(n+E), где n - количество узлов, E - количество ребер в графе. Т.е. алгоритм был быстрее мной предполагаемой сложности. Соответственно, у меня появилась мысль: "а почему бы не обработать тот случай, который ломал алгоритм? Сложность возрастет, ну и пусть, она явно не будет выше квадратичной".

Каждая вершина обрабатывается во внутреннем цикле ровно один раз. Учитывая, что граф обрабатывается списками смежности, то суммарное количество итераций внутреннего цикла -- в точности количество ребер. Если быть более точным, то оценка O(N+E).

Что ж, я попробовал это сделать. Мы немного изменим код и введем новую структуру данных - список очередности обработки узлов графа. Что за список, как он работает?

lst = [key for key in graph.keys()]  # Формируем очередность прохождения узлов графа

Он будет служить нашей итерабельной последовательностью первого цикла. Зачем? Если вдруг у ноды соседом будет уже обработанная нода (т.е. будет проблема, описанная ранее), то мы эту ноду снова будем обрабатывать. Код:

graph = {
    1: {2: 1, 3: 20, 5: 10},
    2: {4: 1},
    3: {5: 1},
    5: {},
    4: {3: 1},
}
lst = [key for key in graph.keys()]  # Формируем очередность прохождения узлов графа
parents = {}  # {Нода: его родитель}
costs = {}  # Минимальный вес для перехода к этой ноде (кратчайшие длины пути до ноды от начального узла)
infinity = float('inf')  # Бесконечность (когда минимальный вес до ноды еще неизвестен)

processed = set()  # Множество обработанных нод
for node in lst:
    if node not in processed:  # Если нода уже обработана не будем ее заново смотреть (иначе м.б. беск. цикл)
        for child, cost in graph[node].items():  # Проходимся по всем детям
            new_cost = cost + costs.get(node,
                                        0)  # Путь до ребенка = путь родителя + вес до ребенка (если родителя нет, то путь до него = 0)
            min_cost = costs.get(child,
                                 infinity)  # Смотрим на минимальный путь до ребенка (если его до этого не было, то он беск.)
            if new_cost < min_cost:  # Если новый путь будет меньше минимального пути до этого,
                costs[child] = new_cost  # то заменяем минимальный путь на вычисленный
                parents[child] = node  # Так же заменяем родителя, от которого достигается мин путь
                if child in processed:  # UPDATE: если ребенок был в числе обработанных
                    lst.append(child)  # Вновь добавляем эту ноду в список для того, чтобы обработать его заново
                    processed.remove(child) # Удаляем из обработанных
        processed.add(node)  # Когда все дети (ребра графа) обработаны, вносим ноду в множество обработанных

print(f'Минимальные стоимости от источника до ноды: {costs}')
print(f'Родители нод, от которых исходит кратчайший путь до этой ноды: {parents}')


def get_shortest_path(start, end):
    '''
    Проходится по родителям, начиная с конечного пути,
    т.е. ищет родителя конечного пути, потом родителя родителя и т.д. пока не дойдет до начального пути.
    Тем самым мы строим обратную цепочку нод, которую мы инвертируем в конце, чтобы получить
    истинный кратчайший путь
    '''
    parent = parents[end]
    result = [end]
    while parent != start:
        result.append(parent)
        parent = parents[parent]
    result.append(start)
    result.reverse()
    shortest_distance = 0
    for i in range(len(result)-1):  # Узнаем кратчайшее расстояние
        node_1 = result[i]
        node_2 = result[i + 1]
        shortest_distance += graph[node_1][node_2]
    result = map(str, result)  # В случае если имена нод будут числами, а не строками (для дальнейшего join)
    print(f'Кратчайший путь от {start} до {end}:  {shortest_distance}')
    return result


shortest_path = get_shortest_path(start=1, end=5)
print('-->'.join(shortest_path))

# -> Кратчайший путь от 1 до 5:  4
# -> 1-->2-->4-->3-->5

По предложенным мне графам проводил тесты, все работает корректно. Пытался сам сломать алгоритм, но не получалось. Я сам не силен в тестировании, поэтому я и прошу помощи на этой площадке, чтобы более компетентные люди попробовали меня опровергнуть. Я все равно считаю на 99.99%, что этот алгоритм не рабочий. Но никак не могу себе это доказать и понять :) Быть может, у Вас, дорогие друзья, получится сломать алгоритм? Если получилось, пришлите мне, пожалуйста, пример графа. Если у Вас есть опровержение, то тоже интересно будет на него взглянуть.

P.S. Что в итоге после некоторых рассуждений?

Алгоритм, похоже, рабочий :)
Ошибся со сложностью Беллмана-Форда. Его сложность составляет O(N*E).

Что касается сложности данного алгоритма, то в наихудшем случае она будет такая же O(N*E). Но я так и не нашел наихудший случай. Во всех случаях, которые я тестировал, он работал быстрее Беллмана-Форда. Давайте рассуждать.

Смоделируем ситуацию "в лоб". Посчитаем количество операций на наихудшем графе, который мне прислали, где алгоритм чувствуте себя несколько хуже, чем на других примерах. Пример графа (извиняюсь за ручной рисунок)

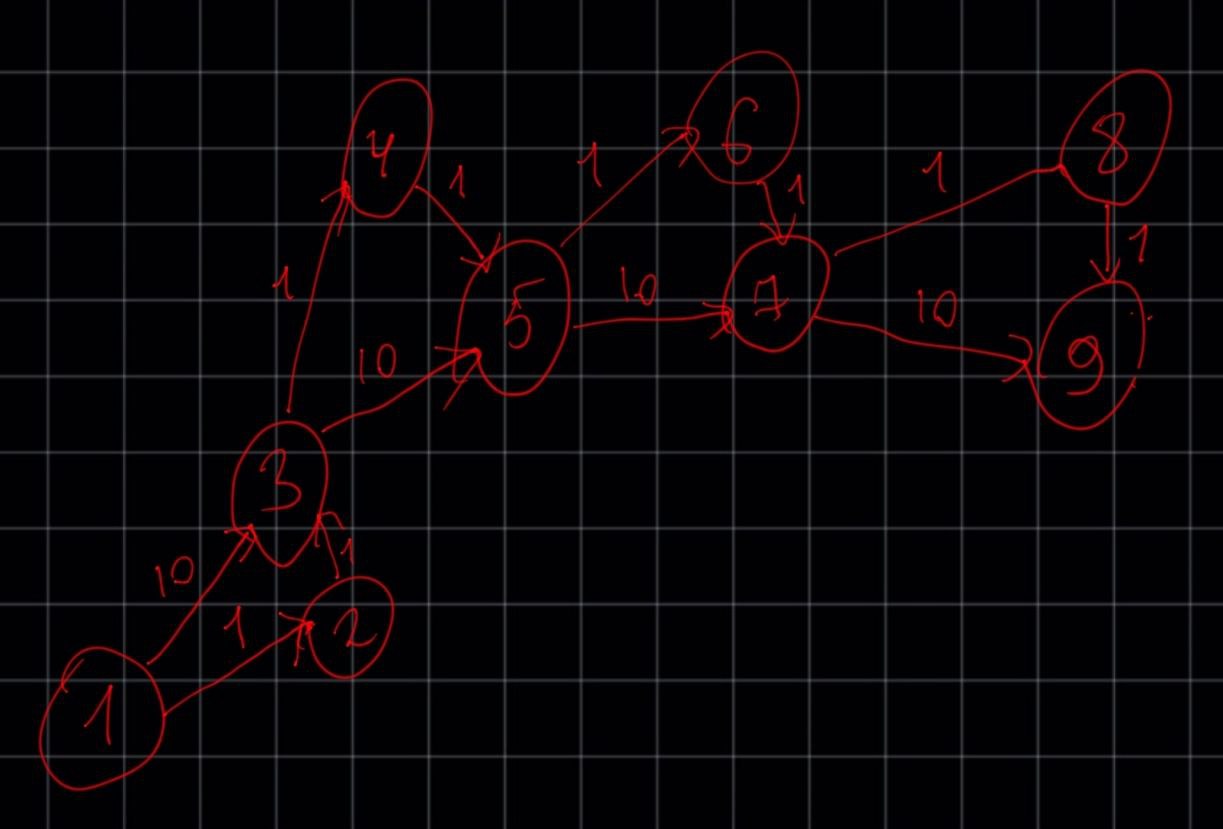
graph = {
  1: {3:10, 2:1}, 

  3: {5:10, 4:1 }, 
  2: {3:1}, 

  5: {7:10, 6:1 }, 
  4: {5:1}, 

  7: {9:10, 8:1}, 
  6: {7:1}, 

  9: {},
  8: {9:1}, 
}

cycle_count = 0
processed = set()  # Множество обработанных нод
for node in lst:
    if node not in processed:  # Если нода уже обработана не будем ее заново смотреть (иначе м.б. беск. цикл)
        for child, cost in graph[node].items():  # Проходимся по всем детям
            cycle_count += 1
            new_cost = cost + costs.get(node,
                                        0)  # Путь до ребенка = путь родителя + вес до ребенка (если родителя нет, то путь до него = 0)
            min_cost = costs.get(child,
                                 infinity)  # Смотрим на минимальный путь до ребенка (если его до этого не было, то он беск.)
            if new_cost < min_cost:  # Если новый путь будет меньше минимального пути до этого,
                costs[child] = new_cost  # то заменяем минимальный путь на вычисленный
                parents[child] = node  # Так же заменяем родителя, от которого достигается мин путь
                if child in processed:  # UPDATE: если ребенок был в числе обработанных
                    lst.append(child)  # Вновь добавляем эту ноду в список для того, чтобы обработать его заново
                    processed.remove(child) # Удаляем из обработанных
        processed.add(node)  # Когда все дети (ребра графа) обработаны, вносим ноду в множество обработанных
        
print(f'Количество операций: {cycle_count}')
# -> Количество операций: 30
# По Беллману-Форду было бы: 9*12=108 судя по формуле

По Беллману-Форду количество операций, судя по формуле, превышает более чем в 3 раза!

Вы можете сказать: "да это просто граф такой попался". Что-ж рассмотрим граф, который является 100% наихудшим случаем для Беллмана-Форда, судя по информации из открытых источников.

Представим такого вида линейный граф: 1-->2-->3-->4-->5. Где каждое ребро имеет вес 1. По Беллману-Форду кол-во операций свелось бы как раз к его формуле (наихудшему случаю), а именно 5*4=20. В моем алгоритме:

graph = {
    1: {2:1},
    2: {3:1},
    3: {4:1},
    4: {5:1},
    5: {},
}
# -> Количество операций: 4

Т.е. по сути за линию выполнил.

Если я что-то неправильно сделал, может быть, глупость совершил, что в "лоб" посчитал количество операций, то с радостью выслушаю, в чем мой "косяк". Но вроде как взял наихудшие случаи.

Таким образом имеем отличный по ассимптотике алгоритм поиска кратчайших путей с отрицательными весами. Быстрее стандартного алгоритма Беллмана-Форда! Спасибо за пояснения и уточнения, если, вдруг, снова нашли какой-то случай уникальный, то, повторюсь, присылайте такой случай. Всем спасибо!

Похоже, я придумал свой алгоритм поиска кратчайшего пути (upd_1: увы, но нет. upd_2: или да?)

Реализация

Сложность

Выводы