https://habrahabr.ru/post/331560/- Разработка под Windows
- Математика
- Python
О чём могут «рассказать» законы распределения случайных величин, если научиться их «слушать»
Законы распределения случайных величин наиболее «красноречивы» при статистической обработке результатов измерений. Адекватная оценка результатов измерений возможна лишь в том случае, когда известны правила, определяющие поведение погрешностей измерения. Основу этих правил и составляют законы распределения погрешностей, которые могут быть представлены представлены в дифференциальной
(pdf) или интегральной
(cdf) формах.
К основным характеристикам законов распределения относятся: наиболее вероятное значение измеряемой величины под названием математическое ожидание
(mean); мера рассеивания случайной величины вокруг математического ожидания под названием среднеквадратическое отклонение
(std).
Дополнительными характеристиками являются – мера скученности дифференциальной формы закона распределения относительно оси симметрии под названием асимметрия
(skew) и мера крутости, огибающей дифференциальной формы под названием эксцесс
(kurt). Читатель уже догадался, что приведенные сокращения взяты из библиотек scipy. stats, numpy, которые мы и будем использовать.
Рассказ о законах распределения погрешности измерений был бы неполным, если не упомянуть об связи между энтропийным и среднеквадратичным значением погрешности. Не утомляя читателей длинными выкладками из информационной теории измерений [1], сразу сформулирую результат.
С точки зрения информации, нормальное распределение приводит к получению точно такого же количества информации, как и равномерное. Запишем выражение для погрешности
delta0 с использованием функций приведённых выше библиотек для распределения случайной величины
x.
Это позволяет заменить любой закон распределения погрешности равномерным с тем же значением
delta0.
Введём ещё один показатель – энтропийный коэффициент k, который для нормального распределения равен:
Следует отметить, что любое распределение отличное от нормального, будет иметь меньший энтропийный коэффициент.
Лучше один раз увидеть, чем семь раз прочитать. Для дальнейшего сравнительного анализа интегральных распределений: равномерного, нормального и логистического модернизируем примеры, приведённые в документации [2].
Программа для нормального распределения:from scipy.stats import norm
import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots(1, 1)
# Calculate a few first moments:
mean, var, skew, kurt = norm.stats(moments='mvsk')
# Display the probability density function (``pdf``):
x = np.linspace(norm.ppf(0.01), norm.ppf(0.99), 100)
ax.plot(x, norm.pdf(x),
'r-', lw=5, alpha=0.6, label='norm pdf')
ax.plot(x, norm.cdf(x),
'b-', lw=5, alpha=0.6, label='norm cdf')
# Check accuracy of ``cdf`` and ``ppf``:
vals = norm.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], norm.cdf(vals))
# True
# Generate random numbers:
r = norm.rvs(size=1000)
# And compare the histogram:
ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2)
ax.legend(loc='best', frameon=False)
plt.show()
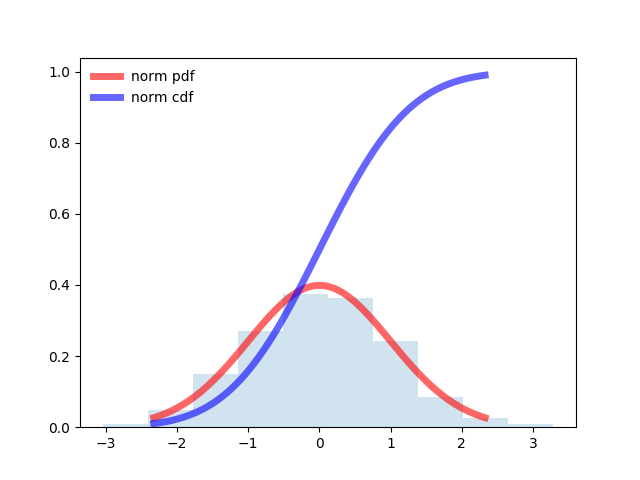
Программа для равномерного распределения:from scipy.stats import uniform
import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots(1, 1)
# Calculate a few first moments:
#mean, var, skew, kurt = uniform.stats(moments='mvsk')
# Display the probability density function (``pdf``):
x = np.linspace(uniform.ppf(0.01), uniform.ppf(0.99), 100)
ax.plot(x, uniform.pdf(x),'r-', lw=5, alpha=0.6, label='uniform pdf')
ax.plot(x, uniform.cdf(x),'b-', lw=5, alpha=0.6, label='uniform cdf')
# Check accuracy of ``cdf`` and ``ppf``:
vals = uniform.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], uniform.cdf(vals))
# True
# Generate random numbers:
r = uniform.rvs(size=1000)
# And compare the histogram:
ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2)
ax.legend(loc='best', frameon=False)
plt.show()
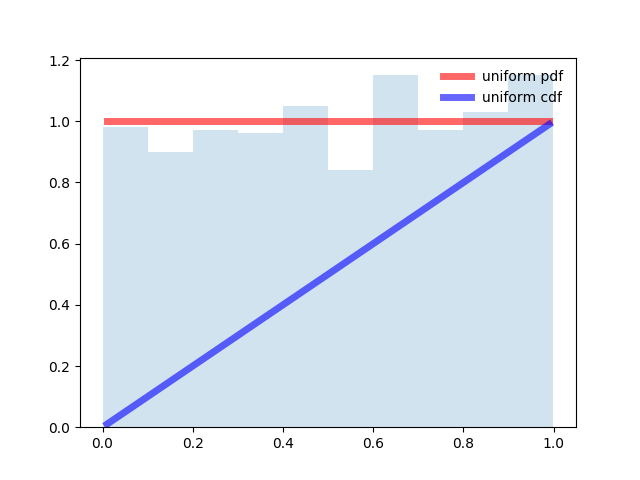
Программа для логистического распределения.from scipy.stats import logistic
import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots(1, 1)
# Calculate a few first moments:
mean, var, skew, kurt = logistic.stats(moments='mvsk')
# Display the probability density function (``pdf``):
x = np.linspace(logistic.ppf(0.01),
logistic.ppf(0.99), 100)
ax.plot(x, logistic.pdf(x),
'g-', lw=5, alpha=0.6, label='logistic pdf')
ax.plot(x, logistic.cdf(x),
'r-', lw=5, alpha=0.6, label='logistic cdf')
vals = logistic.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], logistic.cdf(vals))
# True
# Generate random numbers:
r = logistic.rvs(size=1000)
# And compare the histogram:
ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2)
ax.legend(loc='best', frameon=False)
plt.show()
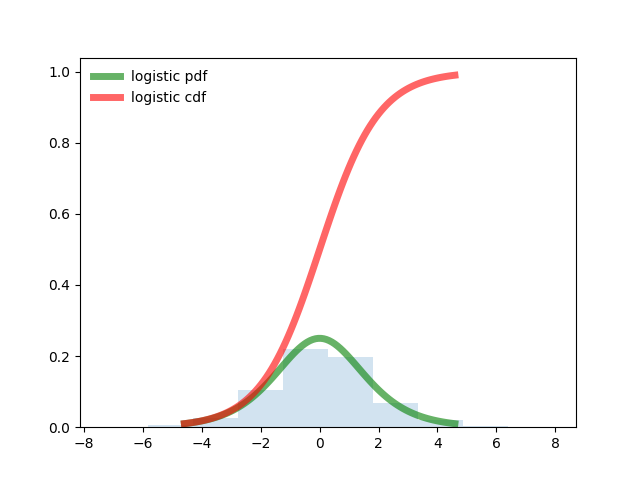
Теперь мы знаем, как выглядят интегральные формы нормального, равномерного и логистического законов и можем приступить к их сравнению с тестовым распределением поставив более общий вопрос — подбора закона распределения случайной величины по данным статистической выборки.
Как подобрать закон распределения, имея интегральное распределения вероятности тестовой выборки
Подготовим первую часть программы, которая будет осуществлять сравнение перечисленных интегральных распределений с тестовой выборкой. Для этого зададим общие для законов распределения основные параметры — математическое ожидание и среднеквадратичное отклонение, используя равномерное распределение.
Первая часть программы предназначена для подготовки к сравнению трёх законов распределения в интегральной форме.from scipy.stats import logistic,uniform,norm,pearsonr
from numpy import sqrt,pi,e
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1)
n=1000# объём выборки
x=uniform.rvs(loc=0, scale=150, size=n)#равномерное распределение
x.sort()#сортировка
print("Математическое ожидание по выборке(общее для сравниваемых распределений) -%s"%str(round(np.mean(x),3)))
print("СКО по выборке(общее для сравниваемых распределений) -%s"%str(round(np.std(x),3)))
print("Энтропийное значение погрешности-%s"%str(round(np.std(x)*sqrt(np.pi*np.e*0.5),3)))
pu=uniform.cdf(x/(np.max(x)))#равномерное интегральное распределение
ax.plot(x,pu, lw=5, alpha=0.6, label='uniform cdf')
pn=norm.cdf(x, np.mean(x), np.std(x))#нормальное интегральное распределение
ax.plot(x,pn, lw=5, alpha=0.6, label='norm cdf')
pl=logistic.cdf(x, np.mean(x), np.std(x))# логистическое интегральное распределение
ax.plot(x,pl, lw=5, alpha=0.6, label='logistic cdf')
Здесь и далее результаты для сравнения введены в функцию print для контроля за ходом вычислений.
Тестовое интегральное распределение и результаты сравнения приведены во второй части программы. В ней определяются коэффициенты корреляции между тестовым и каждым из трёх интегральных законов распределения.
Поскольку коэффициенты корреляции могут отличатся незначительно, введено дополнительное определение возвещённых квадратов отклонения.
Вторая часть программыp=np.arange(0,n,1)/n
ax.plot(x,p, lw=5, alpha=0.6, label='test')
ax.legend(loc='best', frameon=False)
plt.show()
print("Корреляция между нормальным распределением и тестовым - %s"%str(round(pearsonr(pn,p)[0],3)))
print("Корреляция между логистическим распределением и тестовым - %s"%str(round(pearsonr(pl,p)[0],3)))
print("Корреляция между равномерным распределением и тестовым - %s"%str(round(pearsonr(pu,p)[0],3)))
print('Взвешенная сумма квадратов отклонения нормального распределения от теста -%i'%round(n*sum(((pn-p)/pn)**2)))
print('Взвешенная сумма квадратов отклонения логистического распределения от теста -%i'%round(n*sum(((pl-p)/pl)**2)))
print('Взвешенная сумма квадратов отклонения равномерного распределения от теста -%i'%round(n*sum(((pu-p)/pu)**2)))
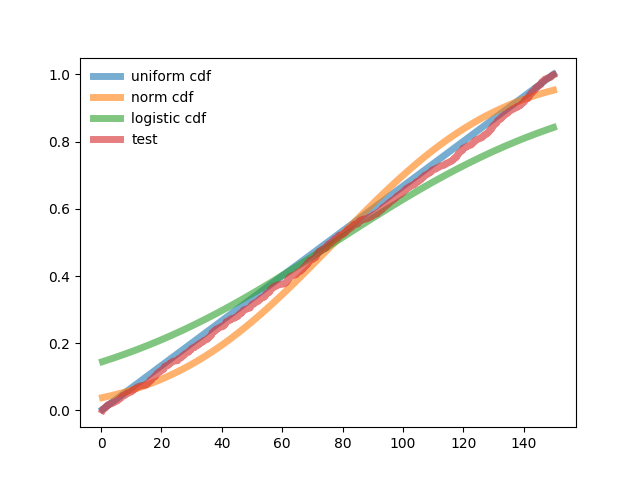
Тестовая функция интегральной формы закона распределения построена в виде ступенчатого накопления –0+ 1/n +2/n+……+1
График и результат роботы программы.
Математическое ожидание по выборке (общее для сравниваемых распределений) -
77.3
СКО по выборке (общее для сравниваемых распределений) -
43.318
Энтропийное значение погрешности-
89.511
Корреляция между нормальным распределением и тестовым —
0.994
Корреляция между логистическим распределением и тестовым —
0.998
Корреляция между равномерным распределением и тестовым —
1.0
Взвешенная сумма квадратов отклонения нормального распределения от теста -
37082
Взвешенная сумма квадратов отклонения логистического распределения от теста -
75458
Взвешенная сумма квадратов отклонения равномерного распределения от теста -
6622
Тестовое распределение вероятностей в интегральной форме является равномерным. При минимальном отличии по коэффициенту корреляции для равномерного распределения взвешенное отклонение от тестового в 5,6 раза меньше, чем у нормального и в 11 раз меньше, чем у логистического.
Вывод
Приведенная реализация подбора закона распределения случайной величины по данным статистической выборки возможно будет полезной при решении аналогичных задач.
1.
Элементы информационной теории измерений.
2.
Statistical functions. 


