http://habrahabr.ru/post/243023/

Привет, уважаемые криптографы и математики!

Мне, не профессиональному математику и не криптографу, бывает сразу сложно понять, как устроен алгоритм шифрования. Перед вами попытка разобраться с отдельными функциями одного алгоритма. А так же, понять, почему Spritz алгоритм сейчас более обсуждаем специалистами, чем, например, Keccak. На Хабре было несколько статей, которые описывали Sponge функцию, или, по-русски, губку (один, два). Эта функция может использоваться несколькими способами: как криптор\декриптор, как хеш, как хеш с раздельными доменами, формировать код аутентичности сообщения (MAC) или имитовставку, работать как потоковый шифр и как потоковый шифр с произвольным доступом, для аутентификации с ассоциированными данными (Authenticated Encryption with Associated Data), как генератор псевдослучайных чисел и для генерации симметричных ключей из паролей.

Что бы разобраться, я использовал оригинальную статью и презентацию, а так же исходные коды с GitHub (Си, JS).

Так как я не специалист, то разбираться начну с примеров. В частности — с функции hash(M, r).

M — входной массив байтов.
r — длина выходного хеш массива в байтах.

Как видно из примера, входной массив имеет длину 3 байта, а выходной 32 байта. Таким образом, длина массива увеличивается на 29 байтов.

Посмотрим как это происходит

Вначале происходит инициализация переменных и массива перестановок.

i = j = k = z = a = 0;
w = 1;

i, j — позиции двух элементов.
к — ключ
z — последнее вычисленное значение.
a — количество использованных полубайтов (нибблов)

Все эти значения изначально равны нулю А массив перестановок изначально имеет упорядоченные значения от 1 до N. В нашем примере N равен 256.

w — ширина хопа равна 1, но может меняться в зависимости от наличия наибольшего общего множителя с N.

Впитываем

Далее вызывается функция absorb(M) — впитывание, как мы помним массив M в примере состоит из 3 байтов. Для определённости пусть это будут байты 'А', 'В' и 'С'. «Губка» имеет довольно большой размер 256 байтов, для наших 3 байтов, которые надо впитать. Для каждого байта вызываем функцию absorbByte('A'), аналогично для 'B' и 'C'.

Каждый байт разбиваем на два ниббла — старший и младший и для каждого из них вызываем функцию absorbNibble('младшие 4 бита'), то же самое для старших 4 битов байта.
Как происходит впитывание текущего ниббла? Функция absorbNibble берёт первый байт из массива перестановок (он равен 1) и помешает его на позицию равную середине массива
перестановок плюс значение самого ниббла. Так как код A равен 65. То младший ниббл равен 1 То новая позиция для первого элемента равна 128+1=129.
А на первой позиции у нас окажется число 129.

Далее мы увеличиваем счётчик использованных ниблов на 1 (a=2).

То же самое проделываем для старшего ниббла и для оставшихся 2 байт. Всего в нашем примере должно быть осуществлено 6 перестановок, по числу использованных нибблов.

Тасуем

После этого запускаем функцию shuffle() — перетасовать.

Вот как она выглядит:

     /*
         Shuffle()
         1 Whip(2N)
         2 Crush()
         3 Whip(2N)
         4 Crush()
         5 Whip(2N)
         6 a=0
       */
       function shuffle() {
         whip(TWO_N);
         crush();
         whip(TWO_N);
         crush();
         whip(TWO_N);
         a = 0;
       }

Первым делом запускается функция update() — обновление 2N раз. Именно в этой функции видны отличия Spritz от RC4 (презентация, анализ).

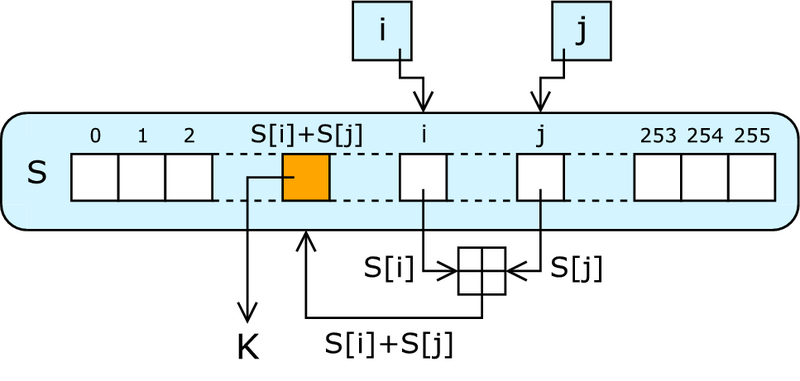
Сравниваем операции с RC4

RC4:

1: i = i + 1
2: j = j + S[i]
3: SWAP(S[i];S[j])
4: z = S[S[i] + S[j]]
5: Return z

Spritz:

1: i = i + w
2: j = k + S[j + S[i]]
2a: k = i + k + S[j]
3: SWAP(S[i];S[j])
4: z = S[j + S[i + S[z + k]]]
5: Return z

Spritz c моей модификацией для лучшего понимания:

1: i = i + w
2: j = j + S[i]
2a: j = k + S[j]
2b: k = i + j
3: SWAP(S[i];S[j])
4a: i = i + S[k+z]   // z=S[j] c предыдущего шага
4b: j = j + S[i]
4c: z = S[j]
5: Return z

Встряхиваем и давим

Появился параметр w — который должен быть нечётным числом. В RC4 он равен всегда 1.
Появился ещё один зависимый параметр k — ключ.
Название функции Whip(2N) можно перевести как встряхивать, а Crush() как давить.

Функция Whip выполняет операции 1,2,2a,3. Затем увеличивает параметр w на единицу столько раз, сколько раз будет найден наибольший общий делитель для w и N.

i пробегает все значения от 1 до 512. Предположим что k=0. Так он установлен при инициализации. Тогда до первой итерации j будет равен 0. А после первой итерации j = S[S[1]], но S[1]=129, и если при absorb первый и 129 элемент переставлялись только один раз, то j=1. Тогда k на шаге 2a примет значение k=129.

Функция Crush() меняет симметричные относительно центра массива перестановок значения, если значение в правой части больше значения в левой части.

Выжимаем

Это итоговая операция squeeze( r ). В нашем выходном массиве\хеше нужно получить r байтов. После вызова drip() и update() выполняется итоговая операция output():

  /*
  Output()
    1 z = S[j+S[i+S[z+k]]]
    2 return z
  */
  function output() {
    z = S[
      madd(j, S[
        madd(i, S[
          madd(z, k)
        ])
      ])
    ];
    return z;
  } 

Как видим, в отличии от RC4 эта операция зависит от вычисленного на предыдущем шаге значения z. Получается несколько фрактальный алгоритм.

Замечаем

Это совершенно новый шифр, пройдёт время, прежде чем появится настоящий анализ. В результате просмотра кода я обратил на следующие особенности.

  /*
    addition modulo N
  */
  function madd(a, b) {
    return (a + b) % N;
    // return (a + b) & 0xff;      // when N = 256, 0xff = N - 1
  }

  /*
    subtraction modulo N. assumes a and b are in N-value range
  */
  function msub(a, b) {
    return madd(N, a - b);
  }

Все суммирования и вычитания делаются по циклическому буферу с размером N (это оговорено в статье). Вероятно, это особенность именно этой реализации, но мне показалось, что в некоторых достаточно простого суммирования или разности. Если я правильно понял, размер буфера может быть различный.

Код чувствителен к начальному значению w. При инициализации этот параметр устанавливается в 1. А что будет, если его установить в N?

Массив перестановок S инициализируется значениями от 1 до N, следовательно S[i]=i, если длина входного буфера маленькая — то это будет верно и на последующих раундах.

При специальном подборе ключа и вектора инициализации (IV), возможно, некоторые операции сильно упростятся. И будут иметь низкую алгебраическую сложность в целом. Например, 2a может быть эквивалентна j=k+(i+j)<<1.

Итого

Очень интересный подход к шифрованию развит в Spritz. По моему мнению, существующие реализации требуют значительной доработки. Также, пройдёт время, прежде чем станут ясно надёжный этот шифр или нет. Уже сейчас видно, что он медленнее, чем RC4. Этот шифр выложен в открытый доступ и не имеет каких либо лицензионных ограничений.

Вероятно, Spritz может стать популярным так как в нём реализованы следующие Sponge functions: AbsorbStop function, Encryption, Hash function, Domain separation hash function, Message Authentication Code (MAC), Authentication Encryption with Associated Data (AEAD), Deterministic Random Bit Generator (DRBG).

Возможно, эти функции можно использовать для распределённых баз данных, для передачи аудио и видео через интернет и т.д.

P.S. Спаисибо Ivan_83 за ссылку Низкая алгебраическая сложность Keccak/Keyak облегчает кубические атаки