Программа
calculator.c родилась как школьный проект в рамках Student Innovation Scholarship. Сперва я решил написать простой инструмент для построения графиков функций с помощью символов ASCII, но после завершения первого прототипа понял, что задача намного сложнее, чем предполагалось. Вернувшись к проекту год спустя, я увидел, что в нём есть много неочевидных нюансов. Поэтому предлагаю разобрать весь процесс разработки моего графического калькулятора с нуля.

Создание ASCII-дисплея
Первая версия калькулятора начинается с массива пикселей, выступающих в качестве графического дисплея. Каждый пиксель содержит один отображаемый символ, а также относительные координаты
x и
y, определяемые границами окна. Помимо этого, инициализация дисплея требует определения этих относительных координат для каждого пикселя, чтобы можно было точно вычислять выход последующей математической функции.
// преобразует индексы пикселей из абсолютных позиций в массив позиций относительно точки отсчёта на плоскости x – y
pixel **quantify_plane(long double x_steps, long double y_steps, long double xmin, long double ymax) {
pixel **display = initialize_display();
for(int y = 0; y < WINDOW_HEIGHT; y++) {
for(int x = 0; x < WINDOW_WIDTH; x++) {
*&display[y][x].x = (xmin + (x_steps * x));
*&display[y][x].y = (ymax - (y_steps * y));
}
}
return display;
}
Здесь
x_steps и
y_steps представляют шаги между каждой парой пикселей с учётом максимального и минимального значений дисплея на каждой оси относительно абсолютного разрешения окна всего дисплея.
// вычисляет ширину и высоту каждого пикселя на плоскости (x, y), используя границы.
long double x_steps = ((xmax-xmin) / WINDOW_WIDTH);
long double y_steps = ((ymax-ymin) / WINDOW_HEIGHT);
Чтобы фактически отрисовать математическую функцию, нам нужно визуализировать координатную плоскость, используя оси
x и
y. Для этого нам потребуется функция, отрисовывающая пустую плоскость
x-y.
// устанавливает для каждого пикселя нужный символ ASCII.
void draw_plane(pixel **display, long double x_steps, long double y_steps) {
long double rel_x, rel_y, output;
for(int y = 0; y < WINDOW_HEIGHT; y++) {
for(int x = 0; x < WINDOW_WIDTH; x++) {
pixel *pixel = &display[y][x];
rel_x = pixel -> x;
rel_y = pixel -> y;
bool x_zero = close_to(rel_x, 0, x_steps/2.1);
bool y_zero = close_to(rel_y, 0, y_steps/2.1);
bool origin = x_zero && y_zero;
if(origin)
pixel -> display = '+';
else if(x_zero)
pixel -> display = '|';
else if(y_zero)
pixel -> display = '-';
else
pixel -> display = ' ';
}
}
}
Функция
close_to решает фундаментальную проблему с использованием ASCII-дисплея, которая заключается в том, что каждый пиксель является не точной точкой на плоскости, а лишь аппроксимацией значений, содержащихся внутри определённой области. В связи с этим нам нужно приблизительно оценить, когда значение попадает в область пикселя, чтобы можно было затенить этот пиксель для правильного отражения вывода математической функции.

Отрисовка функций
После инициализации пустого дисплея, можно приступить к реализации отрисовки на нём математических функций.
К счастью, это делается легко – достаточно затенить пиксель, когда тот представляет вывод заданного метода в собственной относительной координате
x. Для этого мы используем функцию, аналогичную
draw_plane.
// устанавливает отображение пикселя на #, если он аппроксимируется к выводу функции.
void draw_line(pixel **display, long double x_steps, long double y_steps) {
long double rel_x, rel_y, output;
for(int y = 0 ; y < WINDOW_HEIGHT ; y++) {
for(int x = 0 ; x < WINDOW_WIDTH ; x++) {
pixel *pixel = &display[y][x];
rel_x = pixel -> x;
rel_y = pixel -> y;
output = function(rel_x);
if(close_to(output, rel_y, y_steps/2.1))
pixel -> display = '#';
}
}
}
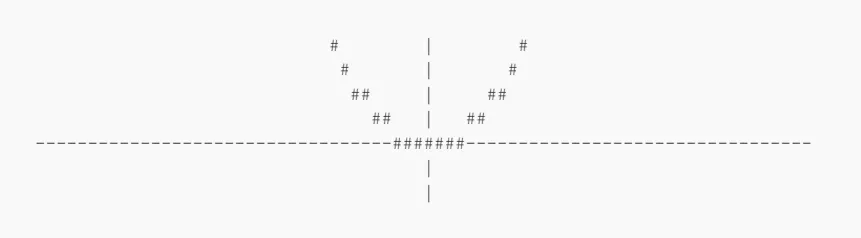
Попробуем выполнить полученный код, используя функцию
x^2.

Итак. Хорошие новости в том, что наш код работает. Но есть и плохие, которые, собственно, очевидны. График выглядит ужасно. Чтобы его исправить, нужно найти источник проблемы. Сейчас мы устанавливаем отображение каждого пикселя на символ решётки, если он аппроксимируется к выводу математической функции, но что, если найти более удачный способ визуально аппроксимировать вывод внутри каждого отдельного пикселя?
▍ Добро пожаловать в мир ASCII-творчества!

Если посмотреть на всевозможные художественные творения с использованием символов ASCII, становится ясно, что нам доступно гораздо больше вариантов отображения символов, нежели одна решётка. И хотя не стоит ожидать, что простой алгоритм достигнет уровня произведений, создаваемых людьми, можно использовать некоторые художественные приёмы использования ASCII, которые позволят значительно улучшить получаемые изображения.
Для максимальной отдачи нам нужно сосредоточиться на области, где наш дисплей больше всего страдает в плане визуальной точности. Высота ячеек символов моноширинного шрифта терминала больше их ширины, значит нам нужен способ искусственно увеличить вертикальное разрешение дисплея. Для этого потребуется определить символы, которые мы хотим использовать.
Если мы сравним символы
'.' и
'-', то увидим, что один слегка выше другого. Используя этот принцип, можно создать ASCII-диапазон, который будет представлять более плавное изменение значения
y. В качестве такого диапазона калькулятор использует
"_,.-~*'`", который хорошо подходит по двум причинам: его можно выводить в любой части терминала, и он представляет ровно то, что нам нужно в плане постепенного перехода между значениями
y.
Чтобы реализовать искусственно растянутое вертикальное разрешение, нам нужно использовать функцию, аппроксимирующую значение
y входных данных внутри пикселя.
Соответствующий код может выглядеть так:
// возвращает символ ASCII на основе того, насколько близко находится значение к концу диапазона.
char ycompress(long double num, long double pixel, long double range) {
char *table = "_,.-~*'`";
// разделяет высоту пикселя на 1/8
long double steps = range/8;
long double goal = num - (pixel - (range/2) );
int counter = 0;
long double step = 0;
while(step < goal) {
step += steps;
counter++;
}
return table[counter - 1];
}
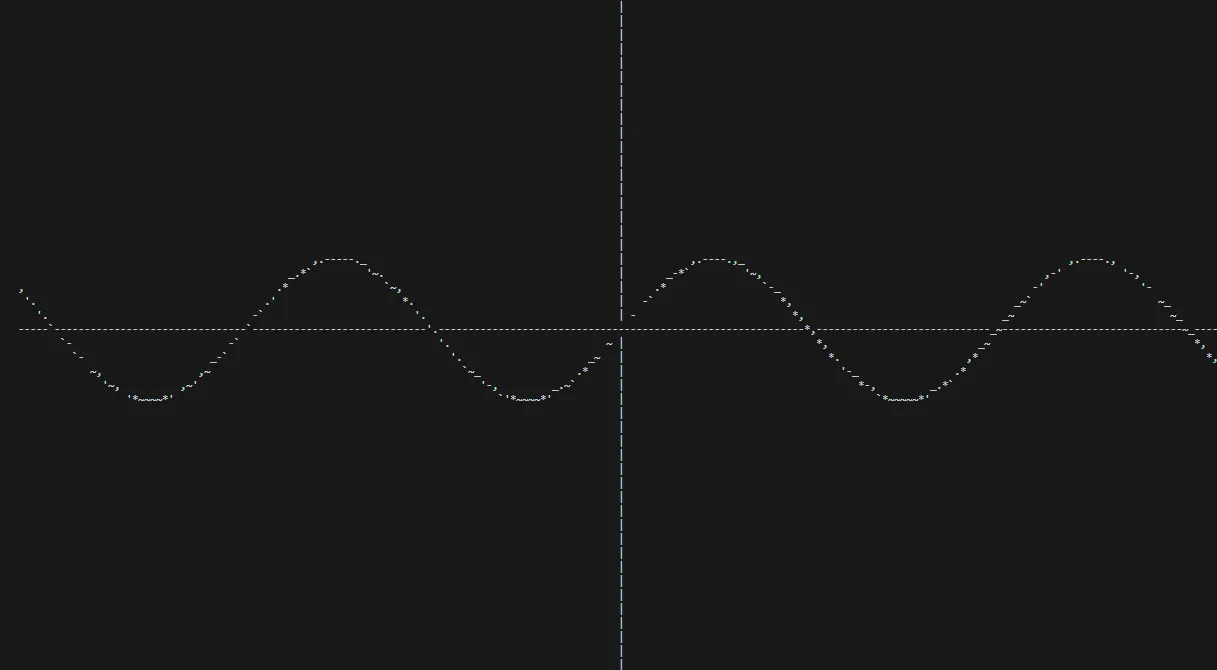
Результаты увеличения вертикального разрешения говорят сами за себя. Вот та же функция
x^2, отрисованная с помощью новой системы:

Мы не только исправили проблему визуальной точности, но также привнесли изящество ASCII, которое и послужило основным вдохновением для создания этой программы.
В текущем состоянии калькулятор выполняет свой графический алгоритм для функции
function, которая получает значение
x и возвращает значение
y. А что, если мы захотим получать ввод от пользователя калькулятора? Реализовать это не так просто, как может показаться. Для получения внешнего ввода нам потребуется парсить математические выражения, что удвоит необходимую работу.

Интерпретация математических выражений
Чтобы проиллюстрировать поставленную задачу, мы используем в качестве примера выражение
x^(2x+4). На первый взгляд для человека нет проблем его вычислить, если будет известно значение
x, но для компьютера всё иначе. Для того, чтобы компьютер правильно вычислил математическое выражение, написанное для человека, потребуется это выражение предварительно обработать. Самый распространённый подход для этого подразумевает переработку такого выражения в легко усваиваемый компьютером формат. Одним из таких форматов является обратная польская запись (Reverse Polish Notation, RPN) или, проще говоря, постфиксная запись.
Прежде чем определять такую запись, нужно более внимательно рассмотреть способ, которым люди записывают выражения. Например, в случае
x^(2x+4) мы видим, что операнды выражения (то есть числа и переменные) размещаются по обе стороны от оператора. Такая запись называется инфиксной, и именно её используют люди. В противоположность ей, постфиксная запись подразумевает расположение операторов после операндов.
Применив это правило к нашему примеру, мы из
x^(2x+4) получим
x2x*4+^. Здесь мы видим два значительных отличия между постфиксной и инфиксной записями, о которых я ещё не говорил. Во-первых, подразумеваемые операции умножения записаны явно, например,
2x становится
2x*, что устраняет с десяток пограничных случаев при последующем вычислении выражения. Во-вторых, после преобразования в постфиксную запись исчезает потребность в скобках, так как вычисление по умолчанию выполняется слева направо. Оба этих отличия значительно повышают производительность, когда дело доходит до алгоритмического вычисления постфиксной записи для каждого ввода функции.
▍ Токенизация строк
Процесс фактического преобразования в постфиксную запись требует отделения операндов от операторов и правильного парсинга скобок во всём уравнении. Это называется токенизацией. Токенизацию строки можно выполнить по-разному, мы же используем для этого конечный автомат. По сути, текущее состояние парсера определяется считанным в этот момент символом, что также определяет, как именно будет токенизирована строка.
Но для начала нам нужно выполнить предварительную обработку выражения, сделав его более алгоритмически усвояемым. Для этого потребуется структура, которая будет хранить все текущие данные парсера. Вот её определение:
// текущие данные парсера.
typedef struct {
char *input;
int pos;
int token_pos;
int token_cnt;
char **tokens;
p_type *types;
p_state state;
char *mkstr;
} p_data;
Здесь у нас изначальное математическое выражение сохраняется в качестве входных данных вместе с инкрементируемыми переменными для сохранения прогресса токенизации. Структуры
p_type и
p_state являются перечислениями, представляющими тип текущего токена и текущее состояние парсера соответственно. Это поможет нам при оценке вывода и логировании ошибок. Наконец, мы определяем
mkstr (функционально аналогична makefile для Cи), где будет храниться вывод предварительно обработанного математического выражения.
Теперь можно начать создавать
mkstr, предварительно обработав и упростив
input. Мы это сделаем в два шага, которые позволят нам далее правильно токенизировать
makestring:
- Заменить все явные математические функции одним символом, их идентифицирующим (например, вставить
s вместо sin, S вместо csc, l вместо log и так далее).
- Вставить в нужных местах символы умножения (например,
2*x вместо 2x и 2*(4) вместо 2(4).
Вот, как эти шаги реализуются в коде Си:
// препроцессинг ввода для создания makestring.
void preprocess(p_data *data) {
int length = strlen(data -> input);
data -> mkstr = (char *) calloc(length * 2, sizeof(char));
// кодирование тригонометрических функций.
char *b_string = (char *) calloc(length, sizeof(char));
for(int i = 0, j = 0; j < length; i++, j++) {
if(isin(data -> input[j], "sctl")) {
if(encode_trig(data -> input + j) != '\0') {
b_string[i] = encode_trig(data -> input + j);
j+=2;
} else data -> state = STATE_err;
} else b_string[i] = data -> input[j];
}
// вставка символа умножения туда, где он должен находиться согласно математической нотации: 2x, xsinx, 3(2-1) и так далее.
for(int i = 0, j = 0; i < strlen(b_string); i++, j++) {
if((isin(b_string[i+1], "sScCtTl" ) && !isin(b_string[i] , "sScCtTl({[/+-*^" ))
|| (isin(b_string[i+1], "([{" ) && !isin(b_string[i] , "([{sScCtTl/+-*^" ))
|| (isin(b_string[i] , ")}]" ) && isin(b_string[i+1], "([{xpesScCtTl1234567890"))
|| (isin(b_string[i] , "0123456789." ) && isin(b_string[i+1], "([{xsScCtTlpe" ))
|| (isin(b_string[i] , "xpe" ) && isin(b_string[i+1], "0123456789sScCtTl([{x" ))) {
data -> mkstr[j] = b_string[i]; j++;
data -> mkstr[j] = '*';
} else { data -> mkstr[j] = b_string[i]; }
} free(b_string);
}
Здесь нам пришлось вручную определить расположение символов умножения, подразумевая каждый пограничный случай, который может включать современная математическая модель.
Теперь, когда у нас есть прекомпилированная
mkstr, можно её токенизировать. Общий процесс токенизации, который мы реализуем, будет включать просмотр и идентификацию каждого символа строки
input. Для этого мы используем функцию, проверяющую тип текущего символа и возвращающую соответствующее ему
p_state. Этот механизм также известен как конечный автомат.
// возвращает текущее состояние парсера на основе типа анализируемого символа.
p_state identify(char c) {
if(isin(c, function_shorthand)) return STATE_trg;
else if(isin(c, "^+/*-")) return STATE_opr;
else if(isin(c, "pe")) return STATE_con;
else if(isin(c, "()[]{}")) return STATE_par;
else if(c == 'x') return STATE_var;
else if((c >= '0' && c <= '9') || c == '.') return STATE_num;
else if(c == '\0' || c == '\n') return STATE_end;
return STATE_err;
}
Заметьте, что использование конечного автомата обеспечивает простую проверку и обработку ошибок.
С помощью этого метода можно перебирать каждый символ во входной строке и определять токен, используя правила, соответствующие каждому типу символов. Важно, что по мере перебора мы будем сохранять тип токена как
p_type в массиве
types. Это поможет нам впоследствии при переупорядочивании и вычислении представленного строкой выражения.
// преобразует строку в токенизированный ввод.
void tokenize(p_data *data) {
if(data -> state == STATE_err) {
throw_error("invalid token");
} data -> state = STATE_str;
// цикл выполнения конечного автомата до завершения строки или возникновения ошибки.
char *curstr = data -> mkstr;
while(data -> state != STATE_err && data -> state != STATE_end) {
switch(data -> state) {
// STATE_str – это состояние по умолчанию, во время которого определяется токен очередного символа.
case STATE_str:
data -> state = identify(curstr[0]); break;
// findnum вызывается в случае числа.
case STATE_num:
data -> types[data -> token_pos] = TYPE_num;
findnum(data, curstr);
data -> state = STATE_str; break;
// скобки рассматриваются как односимвольные токены.
case STATE_par:
data -> types[data -> token_pos] = TYPE_par;
add_ctoken(data, curstr[0]);
data -> state = STATE_str; break;
// переменные рассматриваются как односимвольные токены.
case STATE_var:
data -> types[data -> token_pos] = TYPE_var;
add_ctoken(data, curstr[0]);
data -> state = STATE_str; break;
// если это константа, то она рассматривается как число.
case STATE_con:
data -> types[data -> token_pos] = TYPE_con;
add_ctoken(data, curstr[0]);
if(curstr[0] == 'p') data -> pos++;
data -> state = STATE_str; break;
// тригонометрические функции рассматриваются как односимвольные токены.
case STATE_trg:
data -> types[data -> token_pos] = TYPE_trg;
add_ctoken(data, curstr[0]);
data -> state = STATE_str; break;
// операции рассматриваются как односимвольные токены.
case STATE_opr:
// если операцией является вычитание, то по факту это может быть знак отрицательного числа, а не часть операции.
if(curstr[0] == '-' && (data -> pos == 0 || !isin(data -> mkstr[ + data -> pos - 1], "1234567890)]}xpe"))) {
// для обработки этой ситуации в массив токенов добавляется нулевой токен, и знак минуса начинает рассматриваться как оператор.
data -> types[data -> token_pos] = TYPE_num;
add_ctoken(data, '0');
data -> pos--;
data -> types[data -> token_pos] = TYPE_opr;
add_ctoken(data, curstr[0]);
data -> state = STATE_str;
} else {
data -> types[data -> token_pos] = TYPE_opr;
add_ctoken(data, curstr[0]);
data -> state = STATE_str;
} break;
case STATE_end: return; break;
case STATE_err: return; break;
}
curstr = data -> mkstr + data -> pos;
}
}
Теперь, после успешной токенизации входной строки, можно написать алгоритм, который перестроит полученный массив в постфиксную запись.
▍ Преобразование в постфиксную запись
Для решения проблемы с преобразованием в постфиксную запись нужно подойти к токенизированной строке алгоритмически. Традиционно это делается с помощью так называемого алгоритма сортировочной станции, который действует так:
Перебирает токенизированную строку:
- если текущий токен является операндом, передаёт его на вывод;
- если текущий токен является оператором:
- если оператор, находящийся на вершине стека, в последовательности операций идёт после текущего токена, передаёт вершину стека на вывод;
- в противном случае помещает текущий токен на вершину стека;
- если текущий токен представляет открывающую скобку, передаёт его в стек;
- если текущий токен представляет закрывающую скобку, передаёт на вывод вершину стека, пока не будет встречена открывающая скобка.
Вот реализация этого алгоритма на Си:
// преобразует токены из инфиксной записи (x+2, 2x^3, sin(cos(x)) и т.д.) в постфиксную (x2+, 2x3^*, xcs и т.д.).
void infix_to_postfix(p_data *data) {
int length = strlen(data -> mkstr);
char **output = (char **) calloc(length, sizeof(char*));
char **stack = (char **) calloc(length, sizeof(char*));
int top = 0, output_position = 0, pcount = 0;
if(data -> state == STATE_err) {
throw_error("invalid token");
} data -> state = STATE_str;
// выполняет перебор до конца массива токенов.
for( ; data -> token_pos < data -> token_cnt ; data -> token_pos++) {
switch(data -> types[data -> token_pos]) {
// числа добавляются к выводу сразу же.
case TYPE_num:
output[output_position] = data -> tokens[data -> token_pos];
output_position++;
break;
// операции добавляются в стек в порядке приоритета.
case TYPE_opr:
if(!(stack[top])) {
stack[top] = data -> tokens[data -> token_pos];
} else if(isin(stack[top][0], "[{(")) {
top++;
stack[top] = data -> tokens[data -> token_pos];
} else if(operation_order(data -> tokens[data -> token_pos][0]) > operation_order(stack[top][0])) {
output[output_position] = stack[top];
stack[top] = data -> tokens[data -> token_pos];
output_position++;
} else {
top++;
stack[top] = data -> tokens[data -> token_pos];
}
break;
// переменные рассматриваются как числа.
case TYPE_var:
output[output_position] = data -> tokens[data -> token_pos];
output_position++;
break;
case TYPE_con:
output[output_position] = data -> tokens[data -> token_pos];
output_position++;
break;
// открывающая скобка добавляется в стек; закрывающая инициирует цикл, который выводит вершину стека, пока не будет встречена открывающая скобка.
case TYPE_par:
if(isin(data -> tokens[data -> token_pos][0], "[{(")) {
if(stack[top])
top++;
stack[top] = data -> tokens[data -> token_pos];
} else {
while(!isin(stack[top][0], "[{(")) {
output[output_position] = stack[top];
top--;
output_position++;
}
top--;
if(top >= 0 && isin(stack[top][0], "sScCtTl")) {
output[output_position] = stack[top];
top--;
output_position++;
}
} pcount++;
break;
// тригонометрические функции добавляются в стек и рассматриваются как операции, пока не будут вычислены.
case TYPE_trg:
top++;
stack[top] = data -> tokens[data -> token_pos];
break;
}
}
// добавляет все операции из стека к выводу.
while(top > -1) {
output[output_position] = stack[top];
top--;
output_position++;
}
data -> tokens = output;
data -> token_cnt -= pcount;
data -> token_pos = 0;
}
Здесь мы видим, что главная структура
infix_to_postfix соответствует шаблону функции
tokenize за одним важным отличием – теперь кейсы соответствуют не состоянию парсера, а
p_type текущего индекса в массиве
types. Это экономит нам время не только в текущем выполнении, но и позднее, когда потребуется вычислить результат математического выражения.

Компиляция и вычисление
Теперь, когда у нас есть все необходимые инструменты для компиляции
makestring, осталось лишь собрать их в одну функцию, которую мы сможем вызывать для каждого нового выражения, получаемого в качестве ввода от пользователя.
void compile(p_data *data) {
preprocess(data);
data -> tokens = (char **) calloc(MAX_COMPLEXITY, sizeof(char *));
data -> types = (p_type *) calloc(MAX_COMPLEXITY, sizeof(p_type));
data -> pos = 0;
data -> token_pos = 0;
tokenize(data);
data -> token_cnt = data -> token_pos;
data -> pos = 0;
data -> token_pos = 0;
infix_to_postfix(data);
}
Мы это сделали! Мы официально завершили все необходимые шаги, предшествующие фактическому вычислению результата изначального математического выражения. К счастью, этот этап намного проще, поскольку мы правильно подготовили все нужные для этого ресурсы. Теперь, когда массив
tokens находится в постфиксном представлении, можно использовать стек совместно с циклом для вычисления каждой операции по-отдельности слева направо.
// вычисляет постфиксную строку.
long double evaluate(long double xvalue, p_data *data, long double base) {
long double *stack = calloc(data -> token_cnt, sizeof(long double));
bool *states = calloc(data -> token_cnt, sizeof(bool));
int top = 0;
// перебирает массив токенов до его завершения.
for( ; data -> token_pos < data -> token_cnt ; data -> token_pos++) {
// если встречается операнд, он помещается в стек.
if(isin(data -> tokens[data -> token_pos][0], "1234567890.xpe")) {
if(states[top])
top++;
// x заменяется значением x и передаётся в стек.
if(data -> tokens[data -> token_pos][0] == 'x') {
stack[top] = xvalue;
states[top] = true;
} else if(data -> tokens[data -> token_pos][0] == 'p') {
stack[top] = atan(1) * 4;
states[top] = true;
} else if(data -> tokens[data -> token_pos][0] == 'e') {
stack[top] = exp(1);
states[top] = true;
} else {
stack[top] = atof(data -> tokens[data -> token_pos]);
states[top] = true;
}
} else if(isin(data -> tokens[data -> token_pos][0], "+-/^*sScCtTl")) {
// если встречается оператор, он выполняется с использованием двух верхних элементов стека.
switch(data -> tokens[data -> token_pos][0]) {
case '+':
if(top-1 < 0)
throw_error("invalid operation");
long double sum = stack[top] + stack[top-1];
top--;
stack[top] = sum;
break;
case '-':
if(top-1 < 0)
throw_error("invalid operation");
long double difference = stack[top-1] - stack[top];
top--;
stack[top] = difference;
break;
case '*':
if(top-1 < 0)
throw_error("invalid operation");
long double product = stack[top] * stack[top-1];
top--;
stack[top] = product;
break;
case '/':
if(top-1 < 0)
throw_error("invalid operation");
long double quotient = stack[top-1] / stack[top];
top--;
stack[top] = quotient;
break;
case '^':
if(top-1 < 0)
throw_error("invalid operation");
long double result = (long double) pow(stack[top-1], stack[top]);
top--;
stack[top] = result;
break;
// если встречается тригонометрическая функция, она рассматривается как оператор и выполняется в отношении верхнего элемента стека.
case 's':
if(!states[top])
throw_error("invalid sin");
stack[top] = (long double) sin(stack[top]);
break;
case 'S':
if(!states[top])
throw_error("invalid csc");
stack[top] = (long double) (1/sin(stack[top]));
break;
case 'c':
if(!states[top])
throw_error("invalid cos");
stack[top] = (long double) cos(stack[top]);
break;
case 'C':
if(!states[top])
throw_error("invalid sec");
stack[top] = (long double) (1 / cos(stack[top]));
break;
case 't':
if(!states[top])
throw_error("invalid tan");
stack[top] = (long double) tan(stack[top]);
break;
case 'T':
if(!states[top])
throw_error("invalid cot");
stack[top] = (long double) (1 / tan(stack[top]));
break;
case 'l':
if(!states[top])
throw_error("invalid log");
stack[top] = (long double) (log(stack[top])/log(base));
break;
}
} else {
throw_error("syntax");
}
}
data -> token_pos = 0;
return stack[top];
}
После этого парсинга у нас, наконец, готов рабочий калькулятор. Теперь можно получать пользовательский ввод, сохранять его как строку
input в структуре
p_data и…
 По умолчанию log() имеет основание 10
По умолчанию log() имеет основание 10
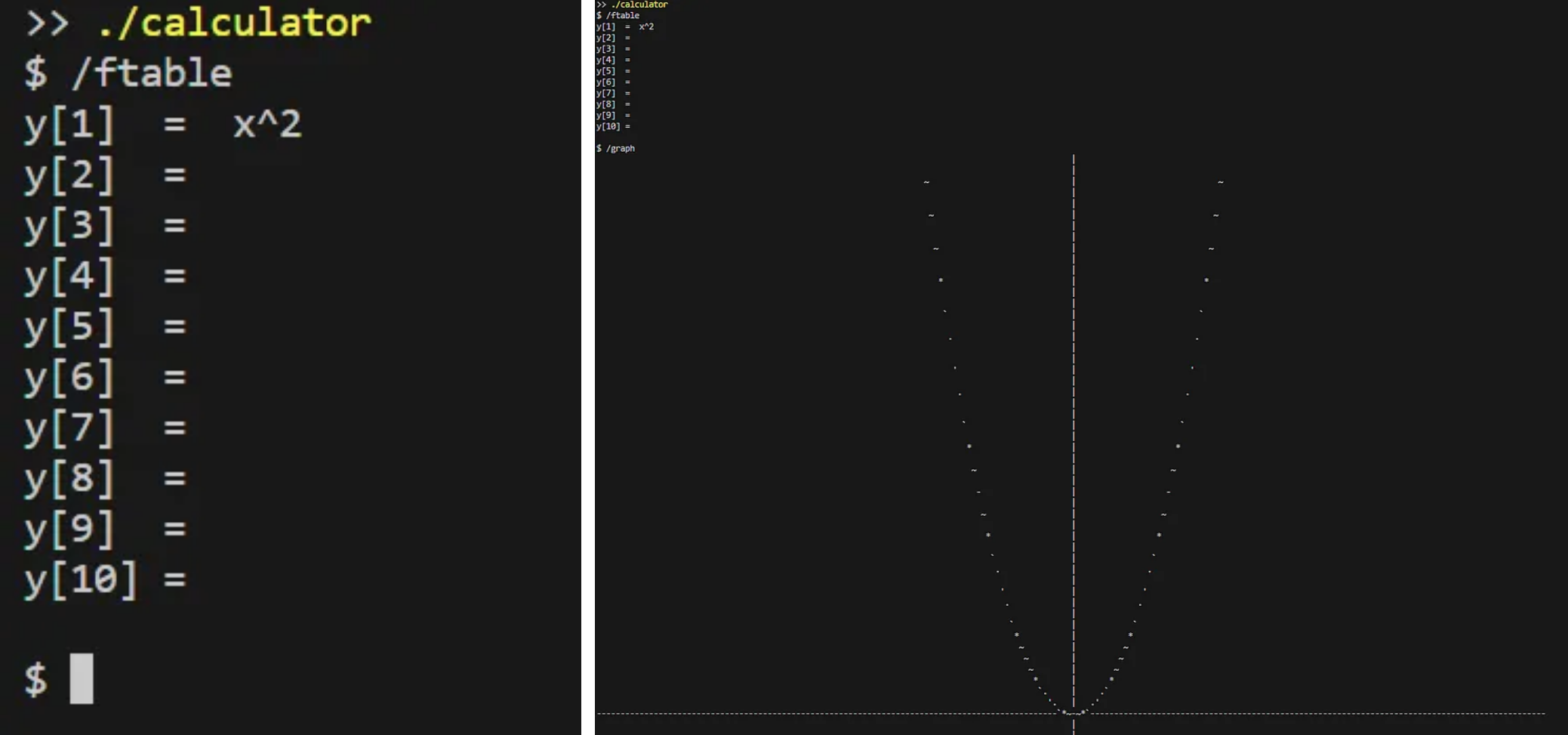
Можно легко адаптировать его под интерфейс стандартного графического калькулятора с помощью команд терминала. Создать таблицу функций для построения графиков пользовательского ввода и сохранить их в файл, в последствии загружая при выполнении программы. То же самое можно сделать и для границ окна. В результате поведение нашей программы будет намного ближе к поведению реального графического калькулятора.
 В таблицу функций предварительно загружена функция y=x²
В таблицу функций предварительно загружена функция y=x²
Но на этом ещё не всё. Изначальной нашей целью было создание калькулятора, и хотя мы этого добились, в нём недостаёт одного элемента, который чётко свяжет всё воедино.

Добавление математического анализа
Вот здесь уже возникают реальные сложности, поскольку без внешних библиотек математического анализа (calculus) попытка в точности реализовать эту функциональность с нуля представляет сущий кошмар, практически тех же масштабов, какие мы только что наблюдали. Поэтому, предлагаю быть сдержанными и ограничить функциональность матанализа в калькуляторе производными и интегралами.
Как это сделать? Как вариант, можно адаптировать формальные определения производной и интеграла, используя очень небольшое значение дельты для достижения максимально точной аппроксимации, необходимой для этого случая.
// возвращает производную на основе определения предела с использованием дельты x.
long double derive(long double x_value, p_data *data, long double b) {
return (evaluate(x_value + DELTA, data, base) - evaluate(x_value, data, b)) / DELTA;
}
И для интегралов…
// возвращает определённый интеграл на основе заданных границ и определения суммирования с использованием дельты x.
long double integrate(long double left_bound, long double right_bound, p_data *function) {
long double x_value = left_bound;
long double def_int = 0;
long double steps = (right_bound - left_bound) * .00001;
while(x_value < right_bound) {
def_int += evaluate(x_value, function, base) * steps;
x_value += steps;
}
return def_int;
}
Очень важно отметить, что поскольку эта программа написана на Си (или, говоря точнее, на компилируемом языке программирования), то, когда дело доходит до использования чисел с плавающей запятой, возникают присущие таким языкам неточности. По факту это является серьёзным ограничением калькулятора, о котором я не упомянул. И хотя сильно оно на результаты вычислений не влияет, при более точных операциях вроде неопределённого интегрирования и получения площади под кривой возникают лёгкие отклонения.
Тем не менее после внесения этих функций в набор команд калькулятора мы всё равно можем спокойно наслаждаться красотой нашей машины матанализа, использующей символы ASCII.
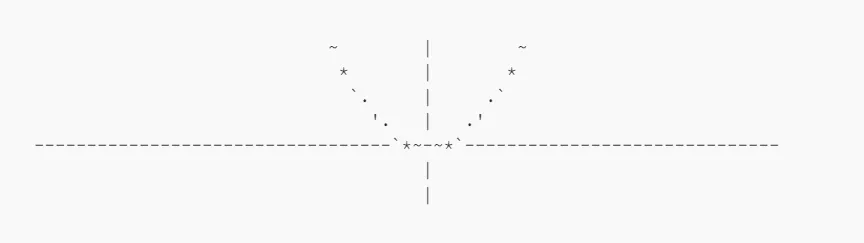
 Слева представлен результат вычисления производной x², а справа – результат определённого интеграла x² для (-3. 3).
Слева представлен результат вычисления производной x², а справа – результат определённого интеграла x² для (-3. 3).
Для выделения интегрируемой затенённой области можно использовать символ решётки.

Завершающие штрихи и ограничения
Теперь нам нужно лишь внести дополнительные удобства вроде команды
/help, возможности изменять основания
log(), а также использовать и устанавливать переменную
x в общих выражениях. После этого мы, наконец, закончим!
Кроме того, наша программа хоть и функциональна, но не идеальна, так как имеет четыре серьёзных ограничения:
- Самое большое – это неточность при вычислениях с плавающей запятой. Это может быть заметно, когда мы работаем со сложными выражениями, используя общую функциональность калькулятора, но в основном проявляется при работе с интегрированием. Вычисляемая площадь под кривой всегда будет немного неточной, хотя и очень близкой к реальной. Мне удалось существенно минимизировать эту погрешность за счёт использования типа
long double вместо float или double, но, к сожалению, полностью компенсировать её не получится.
- Присутствуют неизбежные ограничения при использовании в качестве способа отображения символов ASCII. И хотя это намеренное решение с целью стилизовать калькулятор, всё равно возникает необходимость, чтобы ширина терминала как минимум соответствовала ширине графического дисплея. По умолчанию ширина дисплея составляет 200 символов, так что, если размер шрифта терминала будет достаточно мал, чтобы в строку вмещалось 200 символов, проблем не возникнет.
- В парсере есть один пограничный случай, который не удалось устранить при отладке. По какой-то неизвестной причине, парсер даёт сбой, когда выражение начинается со скобок, сопровождаемых чем-угодно другим. Например,
(x)2, (23)x или (23)+x.
- В калькуляторе реализована очень примитивная система обработки ошибок, не охватывающая интегрирование несуществующих выводов. Поэтому, если вы, например, интегрируете что-либо ниже
log(x), то ввод нижней границы меньше или равной 0 приведёт к ошибке сегментации, потому что невозможно выполнить интегрирование между 0 и значением меньше log(x). Это также касается функций с точками разрыва и других функций с вертикальными асимптотами.
И, возможно, самое большое ограничение заключается в том, что пока для нашего творения нет никакого практического применения, помимо, разве что, тренировки ваших алгоритмических навыков и демонстрации прекрас ASCII.
 Но, честно говоря, разве это можно назвать ограничением?
Но, честно говоря, разве это можно назвать ограничением?
Весь код этого проекта, включая скачиваемые материалы и инструкции, доступен в моём
репозитории github.
Узнавайте о новых акциях и промокодах первыми из нашего Telegram-канала 💰