https://habrahabr.ru/post/279665/

• Математика
• Python

О чем статья?

В этой статье я хочу рассмотреть один из наиболее известных примеров парадокса Симпсона, попутно немного рассказав о MultiIndex в Pandas.
Обо всем по порядку.

Парадокс Симпсона — контринтуитивное явление в Статистике, когда мы видим в каждой из групп данных определенную зависимость, но при объеденении этих групп зависимость исчезает или становится противоположной. Например, если смотреть изменение среднего заработка женщин 25 лет и старше, работающих полный день, между 2000 и 2012 годами с различным уровнем образования, то мы получим следующие цифры (все расчеты проводились с поправкой на инфляцию):

• Less than 9th grade -3.7%
• 9th-12th but didn’t finish -6.7%
• High school graduate -3.3%
• Some college but no degree -3.7%
• Associate’s degree -10.0%
• Bachelor’s degree or more -2.7%

По этим цифрам можно сделать вывод, что заработок женщин за 12 лет снизился. Однако, на самом деле, средний заработок женщин с полной занятостью вырос на 2.8% (подробнее про этот пример можно почитать тут).

Одним из наиболее известных примеров парадокса Симпсона является случай половой дискриминации при поступлении в Калифорнийский унивеситет Berkeley. Его и будем рассматривать далее.

UC Berkeley case

Общая статистика

Поcчитаем долю принятых в университет среди мужчин и женщин (исходные данные можно найти на wiki, весь код лежит на github'e).

import pandas as pd
flat_df = pd.read_csv('berkeley_case.csv', sep = ';')
total_stats = pd.pivot_table(flat_df, aggfunc = sum, index = 'gender', columns = 'param', values = 'number')
total_stats['perc_admitted'] = map(round_2digits, 100*total_stats.accepted/total_stats.applied)

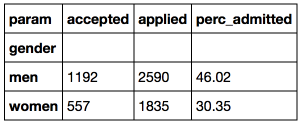
Мы видим, что поступили 46% подавших заявление мужчин и всего 30% женщин. 16% пунктов — это достаточно большая разница и маловероятно, что это просто случайное отклонение. В связи с этим в 1976 году на Berkeley был подан судебный иск за половую дискриминацию.
Однако, закопаемся в данные чуть глубже и посмотрим на процент принятых мужчин и женщин в разбивке по факультетам.

Доля поступивших в разбивке по факультетам

Вот здесь нам и пригодятся MultiIndex или иерархические индексы в Pandas. Иерархические индексы это достаточно полезная функциональность, которая позволяет представлять в табличном виде данные более высоких размерностей и избегать циклов (на мой взгляд, на Pandas код без циклов смотрится более органично, но это, конечно, вкусовщина). Самый понятный способ создания DataFrame с иерархическими индексами это использование функции pivot_table (аналог сводных таблиц в Excel).

df = pd.pivot_table(flat_df, index = 'faculty', values = 'number', columns = ['gender', 'param'])

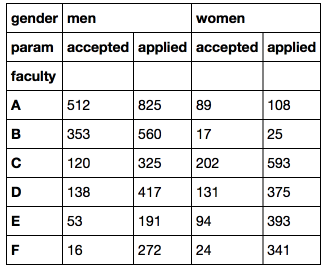
DataFrame с иерархическим индексом можно фильтровать различными способами (подробнее можно почитать в документации)

df['men']['accepted'] # взять определенную колонку в df
df['men'] # отфильтровать колонки на верхнем уровне (level = 0)
# отфильтровать колонки на втором уровне, только accepted
idx = pd.IndexSlice
df.loc[idx[:], idx[:, 'accepted']]

Давайте также посчитаем суммарное количество подавших заявление и поступивших в университет и добавим срез 'total'в исходный DataFrame.

df_total = (df['men'] + df['women']).T # считаем суммарные показатели и сохраняем как отдельный dataframe
df_total['gender'] = 'total'
df_total.set_index('gender', append = True, inplace = True) # добавляем дополнительный уровень в индекс
df_total = df_total.reorder_levels(['gender', 'param']).T # изменяем порядок уровней в индексе
df = pd.concat([df, df_total], axis = 1) # объединяем с исходным df

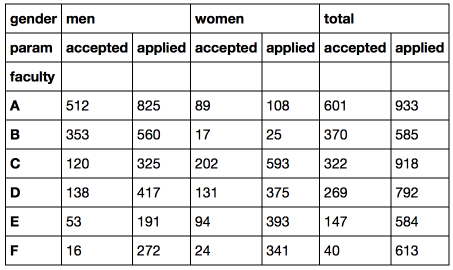
Теперь мы можем легко посчитать процент поступивших среди мужчин, женщин и в общем.

df_inv = df.reorder_levels(['param', 'gender'], axis = 1).sort_index(level = 0, axis = 1) # изменим порядок уровней в индексе для удобства расчетов
admitted_perc = (100*df_inv.accepted/df_inv.applied)
admitted_perc[['total', 'men', 'women']].plot(kind = 'bar', title = 'Percentage of admitted to UC Berkeley')

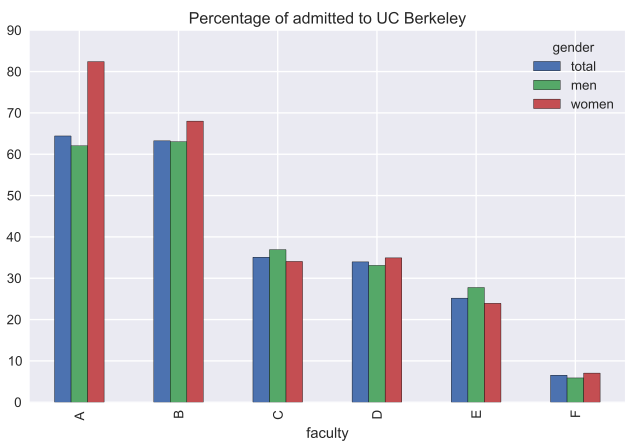
Как оказалось, на большинстве факультетов процент поступивших женщин выше чем у мужчин (для факультета A разница составляет порядка 20% в пользу женщин). На факультетах C и E доля поступивших женщин меньше, но незначительно. Таким образом, гипотеза о половой дискриминации женщин не подтверждается. Для того, чтобы разобраться в этом парадоксе, рассмотрим, на какие факультеты подавали заявление мужчины и женщины.

Популярность факультетов среди мужчин и женщин

Посчитаем распределение заявлений мужчин и женщин по разным факультетам и сравним это со средним процентом поступивших на данный факультет.

gender_faculty_applications = pd.pivot_table(flat_df[flat_df.param == 'applied'], 
                                             index = 'faculty', values = 'number', columns = 'gender')
gender_faculty_applications = gender_faculty_applications.apply(lambda x: 100*x/gender_faculty_applications.sum(), axis = 1)
gender_faculty_applications.columns += '_faculty_share'
faculty_stats = admitted_perc[['total']].join(gender_faculty_applications)
faculty_stats.columns = ['total_perc_admitted', 'men_faculty_share', 'women_faculty_share']
faculty_stats.plot(kind = 'bar', title = 'Statistics on UC Berkeley faculties')

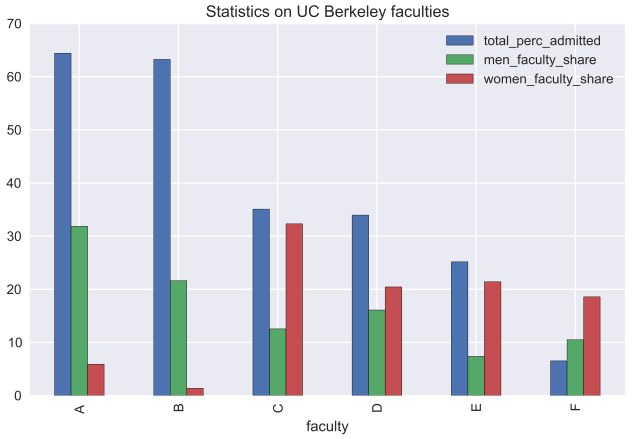
Вот и объяснение парадоксу: большинство мужчин (более 50%) подали заявление на факультеты A и B с высоким процентом поступивших, в то время как большинство женщин решили поступать на более "сложные" факультеты.

В заключении

Мы рассмотрели пример парадокса Симпсона и разобрались, почему нельзя переносить выводы об отдельных группах объектов на объединение этих групп.
Кроме того, познакомились с иерархическими индексами в Pandas, которые позволяют в ряде случаев избежать циклов и упрощают работу с многомерными данными.
Для заинтересовавшихся, советую также посмотреть на эту статью: в ней можно найти интерактивные визуализации, объясняющие парадокс Симпсона.