https://habr.com/ru/post/456176/

• Python
• Data Mining
• Big Data
• Искусственный интеллект

Хабр, привет.

Сегодня у нас пост с интересным заданием — будем обучать логистическую регрессию с L1 и L2 регуляризациями с помощью метода Stochastic Gradient Descent (SGD).



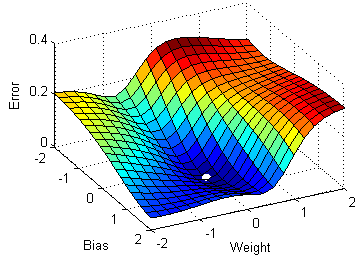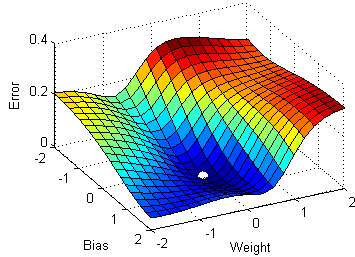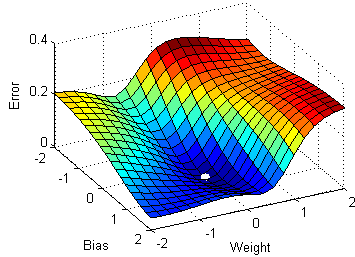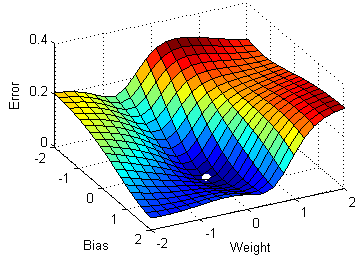
Перед тем как приступить к статье и коду, беглым шагом пробежимся по основным понятиям L1 и L2 регуляризации, логистической регрессии и стахостического градиентного спуска (Stochastic Gradient Descent — SGD).

• Логистическая регрессия;
• L1 регуляризация и L2 регуляризация;
• Стахостический градиентный спуск.

Итак, самое время поставить перед собой цели, которые к концу статьи должны быть достигнуты:

1. Реализовать обучение логистической регрессии с L1 и L2 регуляризациями с помощью метода стахостического градиентного спуска;
2. Для отладки работы алгоритма, реализовать возможность сохранения или вывода ошибки модели, после очередной итерации;
3. Запустить алгоритм на синтетических данных;
4. Вывести полученные веса и нарисовать разделяющую границу между классами;
5. Показать сходимость метода: изобразить графики зависимости значения функции потерь (по всей выборке) после очередной итерации/эпохи (выбрать одно) для разных alpha.

Поехали.

Реализация модели с L1 и L2 регуляризацией с методом SGD

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.base import BaseEstimator, ClassifierMixin
import numpy as np
import math
%matplotlib inline

#Предположим, что в выборке всегда 2 класса
class MySGDClassifier(BaseEstimator, ClassifierMixin):

    def __sigma(self, t):
        t = np.clip(t, -10, 10)
        return 1 / (1 + np.exp(-t))
    #L1 регуляризация
    def __l1_penalty(self):
        return 1/self.C * np.sign(self.theta)
    #L2 регуляризация
    def __l2_penalty(self):
        return 1/self.C * self.theta

    def __none_penalty(self):
        return 0
    
    def __init__(self, **kwargs):
        self.C = kwargs.get('C', 1)
        #Коэф. регуляризации
        self.alpha = kwargs.get('alpha', 1)               
        # Скорость спуска
        self.max_epoch = kwargs.get('max_epoch', 10)      
        #Максимальное количество эпох при обучении модели
        self.chunk_size = kwargs.get('chunk_size', 5)     
        #Количество элементов в чанке (от 1 до общего числа точек)
        self.min_err = kwargs.get('min_err', 0.1)        
        #Пороговое значение ошибки
        penalty = kwargs.get('penalty', 'none')           
        #Способ расчета регуляризации
        
        if penalty == 'l1':
            self.penalty = self.__l1_penalty 
        elif penalty == 'l2':
            self.penalty = self.__l2_penalty
        else:
            self.penalty = self.__none_penalty

        self.theta = None
        self.errors = None
        
    #Обучение модели
    def fit(self, X, y=None):

        import time
        np.random.seed(int(time.time()))
        eps = 1e-15
        n, m = X.shape   
        #n - число строк, m - столбцов        
        sigma = self.__sigma
        chunk_size = self.chunk_size
        errors = np.empty(self.max_epoch)
        errors[:] = np.nan
        X_b = np.c_[X, np.ones(n)]
        self.theta = np.random.randn(m + 1, 1)
        Y = np.vstack(y)

        for epoch in range(self.max_epoch):
            lst = list(range(n))
            np.random.shuffle(lst)
            chunks = [lst[i : i+chunk_size] for i in range(0, n, chunk_size)]
            for chunk in chunks:
                xi = X_b[chunk]
                yi = Y[chunk]
                gradients = xi.T.dot(sigma(xi.dot(self.theta)) - yi)
                self.theta = self.theta - self.alpha * (gradients + self.penalty())
            p = sigma(X_b.dot(self.theta))
            p = np.clip(p, eps, 1-eps)
            epoch_error = 1 / n * np.sum(-(Y * np.log(p) + (1 - Y)*np.log(1 - p)))
            errors[epoch] = epoch_error
            if epoch_error <= self.min_err:
                break
        self.errors = errors
        return self

   #Возвращение метки класса
    def predict(self, X):
        y_hat_proba = self.predict_proba(X)
        y_hat = np.where(y_hat_proba[0] >= 0.5, 0, 1)
        return y_hat

   #Возвращение вероятности каждого из классов
    def predict_proba(self, X):
        if self.theta is None:
            raise Exception("Model is not fitted yet. Use method 'fit'")

        n, m = X.shape
        X_b = np.c_[X, np.ones(n)]
        y1 = self.__sigma(X_b.dot(self.theta))
        y0 = 1 - y1
        y_hat_proba = np.c_[y0, y1]
        return y_hat_proba

Запуск алгоритма на синтетических данных и вывод полученных весов с нарисованной разделяющей границей между классами

max_epoch = 20

C1 = np.array([[0., -0.8], [1.5, 0.8]])
C2 = np.array([[1., -0.7], [2., 0.7]])
gauss1 = np.dot(np.random.randn(200, 2) + np.array([5, 3]), C1)
gauss2 = np.dot(np.random.randn(200, 2) + np.array([1.5, 0]), C2)

X = np.vstack([gauss1, gauss2])
y = np.r_[np.ones(200), np.zeros(200)]

fig, ax = plt.subplots()
fig.set_size_inches(20,10)
ax.scatter(X[:,0], X[:,1], c=y)
x_min, x_max = X[:, 0].min(), X[:, 0].max()
y_min, y_max = X[:, 1].min(), X[:, 1].max()

model = MySGDClassifier(alpha=.01, max_epoch=max_epoch, penalty = 'none', C = 100)
model.fit(X, y)

print("theta = ", model.theta)

t0 = model.theta.item(0)
t1 = model.theta.item(1)
t2 = model.theta.item(2)

x_ = np.array([x_min, x_max])
y_ = -(x_ * t0 + t2) / t1

ax.plot(x_, y_)
ax.set_xlim(x_min - 1, x_max + 1)
ax.set_ylim(y_min - 1, y_max + 1)
plt.show()

Демонстрация сходимости метода с графиками зависимости значения функции потерь после очередной итерации/эпохи для разных alpha

alphas = [0.1, 0.01, 0.001]
penalties = ['None', 'L1', 'L2']
penalty_coef = 10

x_min, x_max = X[:, 0].min(), X[:, 0].max()
y_min, y_max = X[:, 1].min(), X[:, 1].max()

for penalty in penalties:
    fig, ax = plt.subplots(1, 2, figsize=(20, 7))    
    ax[1].scatter(X[:,0], X[:,1], c=y)
   
    ax[0].set_xlim(0, max_epoch)
    ax[0].set_ylim(0.2, 1.5)
    ax[0].set_title('Метод штрафной функции {}'.format(penalty))
    for alpha in alphas:
        model = MySGDClassifier(alpha=alpha, max_epoch=max_epoch, penalty = penalty, C = penalty_coef, min_err = 0.05)
        model.fit(X, y)
        ax[0].plot(range(max_epoch), model.errors, label=r'$\alpha$ = {}'.format(alpha))
        
        t0 = model.theta.item(0)
        t1 = model.theta.item(1)
        t2 = model.theta.item(2)

        x_ = np.array([x_min, x_max])
        y_ = -(x_ * t0 + t2) / t1
        ax[1].plot(x_, y_, label=r'$\alpha$ = {}'.format(alpha))
        ax[1].set_xlim(x_min - 1, x_max + 1)
        ax[1].set_ylim(y_min - 1, y_max + 1)

    ax[0].legend(loc='upper right')    
    ax[1].legend(loc='lower right')    
plt.show()

На этом все наши цели, которые мы ставили перед собой в начале статьи, были достигнуты. Выводы по графикам каждый может сделать сам. Если у кого-то есть, что дополнить или поделиться — пишите в комментариях.

Всем знаний!