http://habrahabr.ru/post/233587/

При построении и анализе поведения решений систем обыкновенных дифференциальных уравнений иногда требуется определять матричную экспоненту [1]. Классический метод связан с тем, что приходится рассчитывать большие степени матриц. В данном топике рассматривается алгоритм приближенного вычисления матричной экспоненты, который за фиксированное число матричных операций дает результат с заданной точностью. Проведен вычислительный эксперимент с целью анализа эффективности алгоритма.
1. Вычисление матричной экспоненты
Вычисление экспоненты
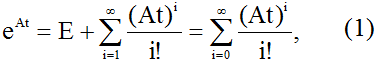
где
E — единичная матрица,
t — время, связано с необходимостью расчета высоких степеней матрица
A. Получим формулу, позволяющую определить матричную экспоненту с помощью
n степеней матрицы
A (
n — ее порядок).
Пусть характеристическое уравнение матрицы
A имеет вид

По теореме Гамильтона-Кэли [2] матрица
A удовлетворяет матричному уравнению, аналогичному (2):

откуда

Следуя методу Д.К. Фаддеева [2], коэффициенты характеристического уравнения определяются по рекуррентному соотношению

где

— след матрицы
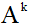
(сумма элементов, стоящих на главной диагонали),
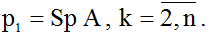
Далее введем обозначение: если
m=0, то

; иначе (при натуральном
m)

Умножим обе части соотношения (3) на матрицу
A с учетом введенных обозначений. Получим

Выражение (5) можно переписать как

Теперь умножим обе части равенства (6) на матрицу
A, подставив при этом в полученное соотношение формулу (3):

Тогда из выражения (7) с помощью последовательного умножения на матрицу
A обеих его частей следует, что

Теперь представим матричную экспоненту как

Откуда имеем

2. Описание алгоритма
Для реализации вычисления матричной экспоненты, согласно (8), был применен следующий алгоритм. Сначала нужно инициировать результат значением нулевой матрицы. Вычислить
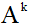
для
k от
0 до
n. Далее выполнить для
k от
0 до
n–1 следующую последовательность операций:
1. Вычислить сумму

. В качестве критерия прекращения суммирования использовать условие

, где
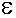
— положительное число, характеризующее точность вычисления суммы.
2. Используя значения, полученные ранее, определить произведение

и прибавить его к текущему значению результата.
При вычислении матричной экспоненты с помощью данного алгоритма используется рекуррентное соотношение (4). При больших значениях
m и
k большинство значений
q будут рассчитываться повторно много раз. Поскольку
q(m,k) является чистой функцией (зависит только от входных аргументов), то будет разумно применить стратегию мемоизации.
Мемоизация — оптимизационная техника, заключающаяся в запоминании результатов вычисления функции для предотвращения множественного расчета значения функции от одних и тех же аргументов. Данная оптимизация позволяет улучшить временные характеристики алгоритма за счет увеличения затрат памяти.
3. Сравнение с классическим алгоритмом
Разработанный алгоритм обеспечивает вычисление матричной экспоненты, используя только
n степеней матрицы, в то время как классический алгоритм (1) не детерминирован, и вычисления степеней матрицы продолжаются, пока не выполнится условие останова алгоритма. Обычно таким условием является

Заметим, что классический алгоритм имеет потребление памяти

. Описанный алгоритм, в виду необходимости хранить
n-1 степень матрицы
A, имеет потребление памяти

.
Нами был проведен вычислительный эксперимент с целью сравнить быстродействие алгоритмов. Для этого была разработана
KipDblK программа из комплекса [3] на языке C++, реализующая оба алгоритма. С помощью данной программы были произведены расчеты матричной экспоненты для матриц различного размера. Порядок матрицы изменялся от
2 до
100. Матрица инициализировалась случайными числами в диапазоне
[0;1]. Экспонента вычислялась для
t=1. Результаты сравнительного эксперимента представлены на рис. 1. По оси абсцисс отложен порядок матрицы
A, по оси ординат — время счета. Полученные точки соединены сплайнами для наглядности.
 Рис. 1. Сравнение временных характеристик классического алгоритма (верхняя кривая) вычисления матричной экспоненты и описанного в данном топике (нижняя кривая).
Рис. 1. Сравнение временных характеристик классического алгоритма (верхняя кривая) вычисления матричной экспоненты и описанного в данном топике (нижняя кривая).P.S.
Данный топик был подготовлен по материалам нашей статьи [4].
Литература
1. Демидович Б.П. Лекции по математической теории устойчивости. — М.: Наука, 1967.
2. Гантмахер Ф.Р. Теория матриц. – М.: Наука, 1967.
3.
KipDblK maxima_comm.tar.gz.
4. Безгин С.В., Пчелинцев А.Н. Организация матричных и символьных вычислений для исследования поведения решений обыкновенных дифференциальных уравнений // Системы управления и информационные технологии, 2012. Т. 47, №1. — С. 4-7.

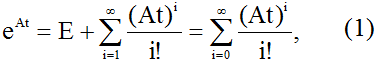




 — след матрицы
— след матрицы 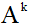 (сумма элементов, стоящих на главной диагонали),
(сумма элементов, стоящих на главной диагонали), 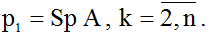
 ; иначе (при натуральном m)
; иначе (при натуральном m)






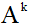 для k от 0 до n. Далее выполнить для k от 0 до n–1 следующую последовательность операций:
для k от 0 до n. Далее выполнить для k от 0 до n–1 следующую последовательность операций: . В качестве критерия прекращения суммирования использовать условие
. В качестве критерия прекращения суммирования использовать условие  , где
, где 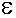 — положительное число, характеризующее точность вычисления суммы.
— положительное число, характеризующее точность вычисления суммы. и прибавить его к текущему значению результата.
и прибавить его к текущему значению результата.
 . Описанный алгоритм, в виду необходимости хранить n-1 степень матрицы A, имеет потребление памяти
. Описанный алгоритм, в виду необходимости хранить n-1 степень матрицы A, имеет потребление памяти  .
.