https://habr.com/ru/post/471194/- Python
- Алгоритмы
- Математика
Привет.
Наверняка всем доводилось быть свидетелями оценки на глазок степени сходства ребенка с родителями: что-нибудь типа «вылитый папа, но на маму тоже похож!!!»

(
взято отсюда)
Как в примере на изображении, можно оценить степень похожести в процентах. Можно задействовать еще родственников, для более точного описания лица малыша в виде взвешенной суммы лиц родни…
И будет это выглядеть и восприниматься вполне естественно для «обычного» человека, не связанного с антропологией, или, например, криминалистикой. Для профессионала в области анализа и распознавания лиц, человеческое лицо представляется, скорее, набором параметров. То есть, точкой (набор координат) в некотором пространстве с базисом (оси, соответствующие параметрам). И если описывать лицо ребенка в сравнении с его родственниками, то скорее всего, точка, соответствующая лицу ребенка окажется в этом пространстве параметров внутри выпуклой оболочки облака точек, соответствующих лицам ближайших родственников (но это не точно).
Собственное, к чему я это все… Эти два подхода к описанию лиц соответствуют двум системам координат:
- барицентрической, описание точки в пространстве (в нашем примере: лица) через взвешенную смесь других точек;
- аффинной, описание точки в пространстве через координаты в некотором базисе.
Так что же такое барицентрические координаты?
Пусть в

-мерном пространстве заданы

точка

с радиус-векторами

,

. Причем, ни одна из точек не лежит в линейной оболочке радиус-векторов остальных точек… Проще говоря, совсем просто: пусть эти точки образуют фигуру, которую нельзя полноценно представить в пространстве с размерностью меньше

.
В случае одномерного пространства (линия), нам необходимы 2 не совпадающие точки, случае двумерного пространства — невырожденный треугольник, в случае трехмерного — тетраэдр.
Тогда любая точка пространства
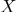
может быть представлена радиус-вектором
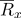
:
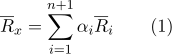
Набор
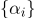
и есть барицентрические координаты.
Чем барицентрические координаты лучше/хуже аффинных?
Пожалуй, начнем с относительных недостатков:
- в барицентрическом представлении нам необходимо на одну координату больше, чем в аффинном;
- расстояние между точками, заданными барицентрически, нельзя напрямую вычислять в этих координатах.
Отчасти первый недостаток компенсируется тем, что не смотря на необходимость использования

барицентрической координаты при описании точки в

-мерном пространстве, количество степеней не повышается. Барицентрические координаты, определенные в формуле (1), связаны соотношением:
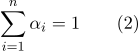
Что касается второго недостатка, если есть необходимость вычисления расстояния между точками, представленными барицентрически, то имеет смысл посчитать скалярные произведения

и использовать аналог расстояния Махаланобиса.
Каковы же бонусы от использования барицентрических координат?
- Барицентрические координаты инвариантны к аффинным преобразованиям пространства. Это свойство используется, например, для линейной интерполяции в компьютерной графике. Пусть в вершинах треугольного элемента поверхности определены текстурные координаты
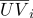 и нормали
и нормали  (
(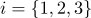 ), тогда каждая точка этого участка поверхности будет обладать барицентрическими координатами
), тогда каждая точка этого участка поверхности будет обладать барицентрическими координатами 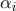 , ее текстурные координаты
, ее текстурные координаты 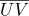 и нормаль
и нормаль 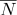 могут быть вычислены как:
могут быть вычислены как:
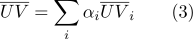
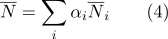
- По барицентрическим координатам легко определить, принадлежит ли точка
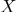 части пространства, ограниченной многогранником с вершинами
части пространства, ограниченной многогранником с вершинами  : это выполняется только в том случае, если
: это выполняется только в том случае, если  . Равенство i-й барицентрической координаты 1 означает, что точка
. Равенство i-й барицентрической координаты 1 означает, что точка  совпадает с
совпадает с  . Если несколько барицентричесих координат равны 0, то это означает, что точка принадлежит подпространству, натянутому на радиус-вектора остальных точек, соответствующие координаты которых больше 0.
. Если несколько барицентричесих координат равны 0, то это означает, что точка принадлежит подпространству, натянутому на радиус-вектора остальных точек, соответствующие координаты которых больше 0.
Наверное, они очень сложно вычисляются?
Не сложнее, чем любое линейное преобразование системы координат. Потому что по сути вычисление барицентрических координат таковым преобразованием и является.
Перепишем радиус-вектора точек в следующем виде:

, где
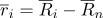
— радус-вектора в системе координат с центром в точке
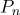
.
Тогда формулу (1) можно переписать в следующем виде:
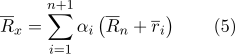
Раскроем скобки в сумме:
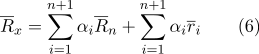
Согласно свойства (2):
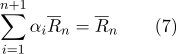
Соответственно:

,
где

Учитывая (2), ограничимся вычислением первых n барицентрических координат. Представим переход в барицентрические координаты как линейное преобразование:

,
где

— вектор n барицентрических координат (кроме последней),

— матрица преобразования.
Учитывая свойства барицентрического представления, если в качестве

подставить один из векторов

(

), то мы получим вектор с нулевыми компонентами, кроме одной i-й, которая будет равна 1.
Если матрицу

умножить на матрицу

, составленную по столбцам из

, то мы должны получить единичную матрицу (матрицу с единицами на главной диагонали и нулями в остальных элементах):

,
где

,

— единичная матрица (

— символ Кронекера: 1, если

, иначе — 0).
Из (10) находим

:

Таким образом, имея набор из точек с радиус-векторами

,

мы можем вычислить матрицу для преобразования в барицентрические координаты:

Используя эту матрицу, мы можем получить первые

барицентрических координат точки

с радиус-вектором

:

Вновь воспользовавшись соотношением (2), получим последнюю барицентрическую координату:

Заключение
Может с первого взгляда барицентрика и кажется неуклюжей и сложной. Но на самом деле, это очень удобный и незаменимый во многих задачах инструмент, к которому довольно быстро привыкаешь. Потому, что тут нет никакой магии, это линейная алгебра в чистом виде!

 с радиус-векторами
с радиус-векторами  ,
,  . Причем, ни одна из точек не лежит в линейной оболочке радиус-векторов остальных точек… Проще говоря, совсем просто: пусть эти точки образуют фигуру, которую нельзя полноценно представить в пространстве с размерностью меньше
. Причем, ни одна из точек не лежит в линейной оболочке радиус-векторов остальных точек… Проще говоря, совсем просто: пусть эти точки образуют фигуру, которую нельзя полноценно представить в пространстве с размерностью меньше 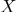 может быть представлена радиус-вектором
может быть представлена радиус-вектором 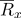 :
: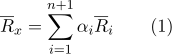
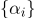 и есть барицентрические координаты.
и есть барицентрические координаты.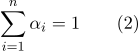
 и использовать аналог расстояния Махаланобиса.
и использовать аналог расстояния Махаланобиса.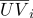 и нормали
и нормали  (
(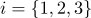 ), тогда каждая точка этого участка поверхности будет обладать барицентрическими координатами
), тогда каждая точка этого участка поверхности будет обладать барицентрическими координатами 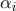 , ее текстурные координаты
, ее текстурные координаты 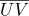 и нормаль
и нормаль 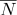 могут быть вычислены как:
могут быть вычислены как: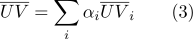
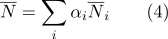
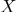 части пространства, ограниченной многогранником с вершинами
части пространства, ограниченной многогранником с вершинами  : это выполняется только в том случае, если
: это выполняется только в том случае, если  . Равенство i-й барицентрической координаты 1 означает, что точка
. Равенство i-й барицентрической координаты 1 означает, что точка  . Если несколько барицентричесих координат равны 0, то это означает, что точка принадлежит подпространству, натянутому на радиус-вектора остальных точек, соответствующие координаты которых больше 0.
. Если несколько барицентричесих координат равны 0, то это означает, что точка принадлежит подпространству, натянутому на радиус-вектора остальных точек, соответствующие координаты которых больше 0. , где
, где 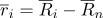 — радус-вектора в системе координат с центром в точке
— радус-вектора в системе координат с центром в точке 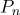 .
.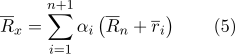
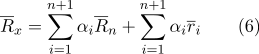
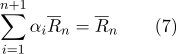
 ,
,  мы можем вычислить матрицу для преобразования в барицентрические координаты:
мы можем вычислить матрицу для преобразования в барицентрические координаты: