https://habr.com/ru/post/458724/

• Python
• Программирование
• Искусственный интеллект

Когда человек учится играть в гольф, большую часть времени он обычно проводит за постановкой базового удара. К другим ударам он подходит потом, постепенно, изучая те или иные хитрости, основываясь на базовом ударе и развивая его. Сходным образом мы пока что фокусировались на понимании алгоритма обратного распространения. Это наш «базовый удар», основа для обучения для большей части работы с нейросетями (НС). В этой главе я расскажу о наборе техник, которые можно использовать для улучшения нашей простейшей реализации обратного распространения, и улучшить способ обучения НС.

Среди техник, которым мы научимся в этой главе: лучший вариант на роль функции стоимости, а именно функция стоимости с перекрёстной энтропией; четыре т.н. метода регуляризации (регуляризации L1 и L2, исключение нейронов [dropout], искусственное расширение обучающих данных), улучшающих обобщаемость наших НС за пределы обучающих данных; лучший метод инициализации весов сети; набор эвристических методов, помогающих выбирать хорошие гиперпараметры для сети. Я также рассмотрю и несколько других техник, чуть более поверхностно. Эти обсуждения по большей части не зависят друг от друга, поэтому их можно по желанию перепрыгивать. Мы также реализуем множество технологий в рабочем коде и используем их для улучшения результатов, полученных для задачи классификации рукописных цифр, изученной в главе 1.

Конечно, мы рассматриваем лишь малую толику огромного количества техник, разработанных для использования с нейросетями. Суть в том, что лучший способ войти в мир изобилия доступных техник – это подробное изучение нескольких самых важных из них. Овладение этими важными техниками не только полезно само по себе, оно ещё углубит ваше понимание того, какие проблемы могут возникать при использовании нейросетей. В итоге вы будете подготовлены для быстрой адаптации новых техник по необходимости.

Функция стоимости с перекрёстной энтропией

Большинству из нас неприятно быть неправым. Вскоре после начала обучения игре на пианино я дал небольшой концерт перед аудиторией. Я нервничал, и начал играть произведение на октаву ниже, чем надо. Я запутался, и не мог продолжать, пока кто-то не указал мне на ошибку. Мне было очень стыдно. Однако, хотя это и неприятно, мы также очень быстро обучаемся, решив, что мы ошиблись. И уж точно в следующий раз, когда я выступал перед аудиторией, я играл в нужной октаве! И наоборот, мы обучаемся медленнее, когда наши ошибки определены не очень хорошо.

В идеале мы ожидаем, что наши нейросети будут обучаться быстро на своих ошибках. Происходит ли это на практике? Для ответа на этот вопрос посмотрим на надуманный пример. В нём участвует нейрон всего с одним входом:



Мы обучаем этот нейрон делать нечто до смешного простое: принять на вход 1 и выдать 0. Конечно, решение такой тривиальной задачи мы могли бы найти, подобрав вес и смещение вручную, не используя обучающий алгоритм. Однако довольно полезно будет попытаться использовать градиентный спуск, чтобы получить в результате обучения вес и смещение. Давайте посмотрим на то, как обучается нейрон.

Для определённости я выберу изначальный вес 0,6 и изначальное смещение 0,9. Это некие общие величины, назначенные в качестве отправной точки, и я не выбирал их специально. Изначально нейрон на выходе выдаёт 0,82, поэтому нам нужно многому научиться, чтобы он приблизился к желаемому выводу 0,0. В оригинале статьи есть интерактивная форма, на которой можно кликнуть «Run» и наблюдать процесс обучения. Это не записанная заранее анимация, браузер реально вычисляет градиент, а потом использует его для обновления веса и смещения, и демонстрирует результат. Скорость обучения η=0,15, достаточно медленная, чтобы могли видеть, что происходит, но достаточно быстрая, чтобы обучение шло за секунды. Функция стоимости С – квадратичная, введённая в первой главе. Я вскоре напомню вам об её точной форме, поэтому не обязательно возвращаться и рыться там. Обучение можно запускать несколько раз, просто нажимая на кнопку «Run».

Как видите, нейрон быстро выучивает вес и смещение, понижающие стоимость, и даёт на выходе 0,09. Это не совсем желаемый результат 0,0, но достаточно неплохой. Допустим, что мы вместо этого выберем начальные вес и смещение 2,0. В данном случае изначальный выход будет равен 0,98, что совсем неверно. Давайте посмотрим, как в этом случае нейрон будет учиться выдавать 0.

Хотя этот пример использует ту же скорость обучения (η=0,15), мы видим, что обучение проходит медленнее. Порядка 150 первых эпох веса и смещения почти не меняются. Затем обучение разгоняется, и, почти как в первом примере, нейрон быстро движется к 0,0. такое поведение странное, не похожее на обучение человека. Как я сказал в начале, мы часто быстрее всего учимся, когда сильно ошибаемся. Но мы только что видели, как наш искусственный нейрон с большим трудом учится, сильно ошибаясь – гораздо труднее, чем когда он ошибался немного. Более того, оказывается, что такое поведение возникает не только в нашем простом примере, но и в НС более общего назначения. Почему обучение идёт так медленно? Можно ли найти способ избежать данной проблемы?

Чтобы понять источник проблемы, вспомним, что наш нейрон обучается через изменение веса и смещения со скоростью, определяемой частными производными функции стоимости, ∂C/∂w и ∂C/∂b. Так что сказать «обучение идёт медленно», это всё равно, что сказать, что эти частные производные малы. Проблема в том, чтобы понять, почему они малы. Для этого давайте вычислим частные производные. Вспомним, что мы используем квадратичную функцию стоимости, которая задаётся уравнением (6):

$$

где a – выход нейрона, когда на входе используется x=1, и y=0 – желаемый выход. Чтобы записать это непосредственно через вес и смещение, вспомним, что a=σ(z), где z=wx+b. Используя цепное правило для дифференцирования по весу и смещению, получаем:

$$

$$

где я подставил x=1 и y=0. Чтобы понять поведение этих выражений, давайте подробнее взглянем на член σ'(z) справа. Вспомним форму сигмоиды:



Из графика видно, что когда выход нейрона близок к 1, кривая становится очень плоской, и σ'(z) становится маленькой. Уравнения (55) и (56) говорят нам о том, что ∂C/∂w и ∂C/∂b становятся очень маленькими. Отсюда и растёт замедление обучения. Более того, как мы увидим чуть позже, замедление обучения происходит, по сути, по той же причине и в НС более общего характера, а не только в нашем простейшем примере.

Представляем функцию стоимости с перекрёстной энтропией

Как нам быть с замедлением обучения? Оказывается, мы можем решить проблему, заменив квадратичную функцию стоимости другой функцией стоимости, известной под названием перекрёстной энтропии. Чтобы понять перекрёстную энтропию, отойдём от нашей простейшей модели. Допустим, мы обучаем нейрон с несколькими входными значениями x₁,x₂,… соответствующими весами w₁,w₂,… и смещением b:



Выход нейрона, конечно, будет a=σ(z), где z=∑_jw_jx_j+b – взвешенная сумма входов. Мы определяем функцию стоимости с перекрёстной энтропией для данного нейрона, как

$$

где n – общее количество единиц обучающих данных, сумма идёт по всем обучающим данным x, а y – соответствующий желаемый выход.

Не очевидно, что у равнение (57) решает проблему замедления обучения. Честно говоря, даже не очевидно, что имеет смысл называть это функцией стоимости! Перед тем, как обратиться к замедлению обучения, посмотрим, в каком смысле перекрёстную энтропию можно интерпретировать как функцию стоимости.

Два свойства в особенности делают разумным интерпретацию перекрёстной энтропии как функции стоимости. Во-первых, она больше нуля, то есть, C>0. Чтобы увидеть это, отметьте, что (а) все отдельные члены суммы в (57) отрицательны, поскольку оба логарифма берутся от чисел в диапазоне от 0 до 1, и (б) перед суммой стоит знак минуса.

Во-вторых, если реальный выход нейрона близок к желаемому выходу для всех обучающих входов x, тогда перекрестная энтропия будет близка к нулю. Для доказательства нам нужно будет предположить, что желаемые выходы y будут равны либо 0, либо 1. Обычно так и бывает при решении проблем классификации, или вычислении булевых функций. Чтобы понять, что происходит, если не делать такого предположения, обратитесь к упражнениям в конце раздела.

Чтобы доказать это, представим, что y=0 и a≈0 for для некоего входного x. Так будет, когда нейрон хорошо обрабатывает такой вход. Мы видим, что первый член выражения (57) для стоимости исчезает, поскольку y=0, а второй будет равен −ln(1−a) ≈0. То же выполняется, когда y=1 и a≈1. Поэтому вклад стоимости будет небольшим, если реальный выход будет близким к желаемому.

Подытоживая, получим, что перекрёстная энтропия положительна, и стремится к нулю, когда нейрон лучше вычисляет желаемый выход y для всех обучающих входов x. Наличия обоих свойств мы ожидаем у функции стоимости. И действительно, оба эти свойства выполняет и квадратичная стоимость. Поэтому, для перекрёстной энтропии это хорошие новости. Однако у функции стоимости с перекрёстной энтропией есть преимущество, поскольку, в отличии от квадратичной стоимости, она избегает проблемы замедления обучения. Чтобы увидеть это, давайте подсчитаем частную производную стоимости с перекрёстной энтропией по весам. Подставим a=σ(z) в (57), дважды применим цепное правило, и получим:

$$

$$

Приводя к общему знаменателю и упростив, получим:

$$

Используя определение сигмоиды, σ(z)=1/(1+e^−z) и немножко алгебры, можно показать, что σ′(z) = σ(z)(1 − σ(z)). Проверить это я попрошу вас в упражнении далее, но пока что примем это, как истину. Члены σ′(z) и σ(z)(1−σ(z)) сокращаются, и это приводит к

$$

Прекрасное выражение. Из него следует, что скорость, с которой обучаются веса, контролируется σ(z)−y, то есть, ошибкой на выходе. Чем больше ошибка, тем быстрее обучается нейрон. Этого можно было интуитивно ожидать. Этот вариант избегает замедления обучения, вызванного членом σ’(z) в аналогичном уравнении для квадратичной стоимости (55). Когда мы используем перекрёстную энтропию, член σ’(z) сокращается, и нам уже не приходится волноваться о его малости. Это сокращение – особое чудо, гарантируемое функцией стоимости с перекрёстной энтропией. На самом деле, конечно, это не совсем чудо. Как мы увидим позднее, перекрёстную энтропию специально выбрали именно за это свойство.

Сходным образом можно вычислить частную производную для смещения. Не буду приводить заново все детали, но можно легко проверить, что

$$

Это опять-таки помогает избежать замедления обучения из-за члена σ’(z) в аналогичном у равнении для квадратичной стоимости (56).

Упражнение

• Проверьте, что σ′(z) = σ(z)(1 − σ(z)).

Вернёмся к нашему надуманному примеру, с которым мы игрались ранее, и посмотрим, что случится, если вместо квадратичной стоимости мы будем использовать перекрёстную энтропию. Чтобы настроиться, мы начнём со случая, в котором квадратичная стоимость отлично сработала, когда начальный вес был 0,6 а смещение – 0,9. В оригинале статьи есть интерактивная форма, в которой можно нажать кнопку «Run» и посмотреть, что происходит при замене квадратичной стоимости на перекрёстную энтропию.

Ничего удивительного, нейрон в данном случае обучается прекрасно, как и ранее. Теперь посмотрим на случай, в котором раньше нейрон застревал, с весом и смещением, начинающимися с величины 2,0.



Успех! На этот раз нейрон обучился быстро, как мы и хотели. Если наблюдать пристально, можно увидеть, что наклон кривой стоимости изначально более крутой, по сравнению с плоским регионом соответствующей кривой квадратичной стоимости. Эту крутость даёт нам перекрёстная энтропия, и не даёт застрять там, где мы ожидаем наискорейшее обучение нейрона, когда он начинает с очень больших ошибок.

Я не сказал, какая скорость обучения использовалась в последних примерах. Ранее с квадратичной стоимостью мы использовали η=0,15. Должны ли мы использовать такую же скорость и в новых примерах? На самом деле, меняя функцию стоимости, нельзя точно сказать, что значит – использовать «такую же» скорость обучения; это будет сравнения яблок с апельсинами. Для обеих функций стоимости я экспериментировал, подыскивая скорость обучения, позволяющую увидеть происходящее. Если вам всё же интересно, то в последних примерах η=0,005.

Вы можете возразить, что изменение скорости обучения лишает графики смысла. Кому какая разница, как быстро обучается нейрон, если мы могли произвольно выбирать скорость обучения? Но это возражение не учитывает главного. Смысл графиков не в абсолютной скорости обучения, а в том, как меняется эта скорость. При использовании квадратичной функции обучение идёт медленнее, если нейрон сильно ошибается, а потом идёт быстрее, когда нейрон подходит к нужному ответу. С перекрёстной энтропией обучение идёт быстрее, когда нейрон сильно ошибается. И эти утверждения не зависят от заданной скорости обучения.

Мы исследовали перекрёстную энтропию для одного нейрона. Однако это легко обобщить на сети со многими слоями и многими нейронами. Допустим, что y=y₁, y₂,… — желаемые значения выходных нейронов, то есть, нейронов в последнем слое, а a^L₁, a^L₂,… — сами выходные значения. Тогда перекрёстную энтропию можно определить, как:

$$

Это то же самое, что уравнение (57), только теперь наша ∑_j суммирует по всем выходным нейронам. Не буду подробно разбирать производную, однако разумно предположить, что с использованием выражения (63) мы можем избежать замедления в сетях с многими нейронами. Если интересно, вы можете взять производную в задаче ниже.

Между прочим, используемый мною термин «перекрёстная энтропия» запутал некоторых ранних читателей книги, поскольку он противоречит другим источникам. В частности, нередко перекрёстную энтропию определяют для двух распределений вероятности, pj
и qj, как ∑_jp_jlnq_j. Это определение можно связать с (57), если считать один сигмоидный нейрон выдающим распределение вероятности, состоящее из активации нейрона a и дополняющей её величины 1-a.

Однако, если у нас в последнем слое много сигмоидных нейронов, вектор a^L_j обычно не даёт распределения вероятностей. В итоге определение типа ∑_jp_jlnq_j лишено смысла, поскольку мы не работаем с распределениями вероятности. Вместо этого (63) можно представлять себе, как просуммированный набор перекрёстных энтропий каждого нейрона, где активация каждого нейрона интерпретируется как часть двухэлементного распределения вероятности (конечно, в наших сетях нет никаких вероятностных элементов, поэтому это на самом деле никакие не вероятности). В этом смысле (63) будет обобщением перекрёстной энтропии для распределений вероятностей.

Когда использовать перекрёстную энтропию вместо квадратичной стоимости? На самом деле, перекрёстную энтропию почти всегда будет использовать лучше, если выходные нейроны у вас сигмоидные. Чтобы понять это, вспомним, что настраивая сеть, мы обычно инициализируем веса и смещения при помощи некоего случайного процесса. Может так получиться, что этот выбор приведёт к тому, что сеть будет совершенно неверно интерпретировать некие обучающие входные данные – к примеру, выходной нейрон будет стремиться к 1, когда должен стремиться к 0, или наоборот. Если мы используем квадратичную стоимость, которая замедляет обучение, она не остановит обучение совсем, поскольку веса будут продолжать обучаться на других обучающих примерах, но такая ситуация, очевидно, является нежелательной.

Упражнения

• Один подвох перекрёстной энтропии состоит в том, что сначала может быть трудно запомнить соответствующие роли y и a. Легко запутаться, как будет правильно, −[ylna+(1−y)ln(1−a)] или −[alny+(1−a)ln(1−y)]. Что будет со вторым выражением, когда y=0 или 1? Влияет ли эта проблема на первое выражение? Почему?
• В обсуждении единственного нейрона в начале раздела, я говорил, что перекрёстная энтропия мала, если σ(z)≈y для всех обучающих входящих данных. Аргумент основывался на том, что y равен 0 или 1. Обычно в задачах классификации так и есть, но в других задачах (например, регрессии) y иногда может принмать значения между 0 и 1. Покажите, что перекрёстная энтропия всё равно минимизируется, когда σ(z)=y для всех обучающих входов. Когда так происходит, значение перекрёстной энтропии равно

  $$

  . Величину −[ylny+(1−y)ln(1−y)] иногда называют бинарной энтропией.

Задачи

• Многослойные сети с многими нейронами. В записи из последнего раздела покажите, что для квадратичной стоимости частная производная по весам в выходном слое равна

  $$

  Член σ'(z^L_j) заставляет обучение замедляться, когда нейрон склоняется к неверному значению. Покажите, что для функции стоимости с перекрёстной энтропией выходная ошибка δ^L для одного обучающего примера x задаётся уравнением

  $$

  Используйте это выражение, чтобы показать, что частная производная по весам в выходном слое задаётся уравнением

  $$

  Член σ'(z^L_j) исчез, поэтому перекрёстная энтропия избегает проблемы замедления обучения, не только при использовании с одним нейроном, но и в сетях с многими слоями и многими нейронами. С небольшим изменением этот анализ подходит и для смещений. Если это неочевидно для вас, вам лучше проделать и этот анализ также.
• Использование квадратичной стоимости с линейными нейронами во внешнем слое. Допустим, у нас многослойная сеть с многими нейронами. Допустим, в финальном слое все нейроны линейные, то есть сигмоидная функция активации не применяется, а их выход просто определяется, как a^L_j = z^L_j. Покажите, что при использовании квадратичной функции стоимости выходная ошибка δL для одного обучающего примера x задаётся

  $$

  Как и в прошлой задаче, используйте это выражение, чтобы показать, что частные производные по весам и смещениям во внешнем слое определяются, как

  $$

  $$

  Это показывает, что если выходные нейроны линейные, тогда квадратичная стоимость не вызовет никаких проблем с замедлением обучения. В этом случае квадратичная стоимость вполне подходит для использования.

Использование перекрёстной энтропии для классификации цифр из MNIST

Перекрёстную энтропию легко реализовать в виде части программы, обучающей сеть при помощи градиентного спуска и обратного распространения. Позже мы сделаем это, разработав улучшенную версию нашей ранней программы классификации рукописных цифр из MNIST, network.py. Новая программа называется network2.py, и включает не только перекрёстную энтропию, но и несколько других техник, разработанных в этой главе. А пока посмотрим, насколько хорошо наша новая программа классифицирует цифры MNIST. Как и в главе 1, мы будем использовать сеть с 30 скрытыми нейронами, и мини-пакетом размером в 10. Установим скорость обучения η=0,5 и будем обучаться 30 эпох.

Как я уже говорил, нельзя точно сказать, какая скорость обучения подойдёт в каком случае, поэтому я экспериментировал с подбором. Правда, существует способ очень грубо эвристически связать скорость обучения с перекрёстной энтропией и квадратичной стоимостью. Раньше мы видели, что в членах градиента для квадратичной стоимости есть дополнительный член σ'=σ(1-σ). Допустим, мы усредним эти значения для σ, ∫¹₀dσ σ (1−σ)=1/6. Видно, что (очень грубо) квадратичная стоимость в среднем обучается в 6 раз медленнее для той же скорости обучения. Это говорит о том, что хорошей отправной точкой будет поделить скорость обучения для квадратичной функции на 6. Конечно, это совершенно не строгий аргумент, и не стоит принимать его слишком серьёзно. Но он иногда может быть полезным в качестве отправной точки.

Интерфейс для network2.py немного отличается от network.py, но всё равно должно быть понятно, что происходит. Документацию по network2.py можно получить при помощи команды help(network2.Network.SGD) в оболочке python.

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data,
... monitor_evaluation_accuracy=True)

Отметьте, кстати, что команда net.large_weight_initializer() используется для инициализации весов и смещений так же, как описано в главе 1. Нам нужно прогнать её, потому что позже мы изменим инициализацию весов по умолчанию. В итоге, после запуска всех указанных выше команд, мы получим сеть, работающую с точностью в 95,49%. Это очень близко к результату из первой главы, 95.42%, использовавшему квадратичную стоимость.

Давайте также посмотрим на случай, где мы используем 100 скрытых нейронов и перекрёстную энтропию, а всё остальное оставляем таким же. В этом случае точность получается 96,82%. Это серьёзное улучшение по сравнению с результатами из первой главы, где мы достигли точности в 96.59%, используя квадратичную стоимость. Изменение может показаться небольшим, но подумайте о том, что ошибка упала с 3,41% до 3,18%. То есть, мы устранили примерно 1/14 ошибок. Это довольно неплохо.

Довольно приятно, что функция стоимости с перекрёстной энтропией даёт нам сходные или лучшие результаты по сравнению с квадратичной стоимостью. Однако они не доказывают однозначно, что перекрёстная энтропия – лучший выбор. Дело в том, что я вовсе не старался выбирать гиперпараметры – скорость обучения, размер мини-пакета, и т.д. Чтобы улучшение получилось более убедительным, нам нужно как следует заняться их оптимизацией. Но результаты всё равно вдохновляющие, и подтверждают наши теоретические выкладки о том, что перекрёстная энтропия – лучший выбор, чем квадратичная функция стоимости.

В этом ключе пройдёт вся эта глава и, в принципе, остаток книги. Мы будем вырабатывать новую технику, испытывать её, и получать «улучшенные результаты». Конечно, хорошо, что мы видим эти улучшения. Но интерпретировать их всегда сложно. Убедительно будет только, если мы увидим улучшения после серьёзной работы по оптимизации всех остальных гиперпараметров. А это довольно сложная работа, требующая больших вычислительных ресурсов, и обычно мы не будем заниматься таким тщательным расследованием. Вместо этого мы будем идти дальше на базе неформальных тестов, как тех, что приведены выше. Но вам нужно иметь в виду, что такие тесты не являются однозначным доказательством, и внимательно следить за теми случаями, когда аргументы начинают сбоить.

Пока что мы подробно обсуждали перекрёстную энтропию. Зачем тратить столько сил, если она даёт такое небольшое улучшение наших результатов по MNIST? Позже в этой главе мы увидим другие техники – в частности, регуляризацию – дающие куда как более сильные улучшения. Так зачем мы концентрируемся на перекрёстной энтропии? В частности потому, что перекрёстная энтропия – это часто используемая функция стоимости, поэтому в ней стоит хорошо разобраться. Но более важной причиной будет то, что насыщение нейронов – важная в области нейросетей проблема, к которой мы будем постоянно возвращаться на протяжении книги. Поэтому я так подробно обсуждал перекрёстную энтропию, поскольку это хорошая лаборатория для того, чтобы начать разбираться в насыщении нейронов и в том, как можно искать подходы к этой проблеме.

Что означает перекрёстная энтропия? Откуда она берётся?

Наше обсуждение перекрёстной энтропии вращалось вокруг алгебраического анализа и практической реализации. Это полезно, но в итоге остаются без ответа более широкие концептуальные вопросы, например: что означает перекрёстная энтропия? Есть ли интуитивный способ её представлять? Как люди вообще могли придумать перекрёстную энтропию?

Начнём с последнего: что могло подвигнуть нас на размышление о перекрёстной энтропии? Допустим, мы обнаружили замедление обучения, описанное ранее, и поняли, что его причиной были члены σ'(z) в уравнениях (55) и (56). Немного поглазев на эти уравнения, мы могли бы задуматься, нельзя ли выбрать такую функцию стоимости, чтобы член σ'(z) исчез. Тогда стоимость C = C_x одного обучающего примера удовлетворяла бы уравнениям:

$$

$$

Если бы мы выбрали функцию стоимости, делающую их истинными, то они бы довольно просто описали бы интуитивное понимание того, что чем больше изначальная ошибка, тем быстрее обучается нейрон. Они бы также устранили проблему с замедлением обучения. На самом деле, начав с этих уравнений, мы бы показали, что возможно вывести форму перекрёстной энтропии, просто следуя математическому чутью. Чтобы увидеть это, отметим, что, исходя из цепного правила, мы получаем:

$$

Используя в последнем уравнении σ′(z) = σ(z)(1−σ(z)) = a(1−a), получим:

$$

Сравнив с уравнением (72), получим:

$$

Интегрируя это выражение по a, получим:

$$

Это вклад отдельного обучающего примера x в функцию стоимости. Чтобы получить полную функцию стоимости, нам нужно усреднить по всем обучающим примерам, и мы приходим к:

$$

Константа тут – средняя по отдельным константам каждого из обучающих примеров. Как видим, уравнения (71) и (72) уникальным образом определяют форму перекрёстной энтропии, плоть до общей константы. Перекрёстную энтропию не доставали волшебным образом из воздуха. Её можно было найти простым и естественным образом.

Что насчёт интуитивного представления о перекрёстной энтропии? Как нам её себе представлять? Подробное объяснение привело бы к тому, что мы бы обогнали наш учебный курс. Однако можно упомянуть о существовании стандартного способа интерпретации перекрёстной энтропии, происходящего из области теории информации. Грубо говоря, перекрёстная энтропия – это мера неожиданности. Например, наш нейрон пытается подсчитать функцию x→y=y(x). Но вместо этого он подсчитывает функцию x→a=a(x). Допустим, мы представляем себе a, как оценку нейроном вероятности того, что y=1, а 1-a – вероятность того, что правильным значением для y будет 0. Тогда перекрёстная энтропия измеряет то, насколько мы «удивлены», в среднем, когда обнаруживаем истинное значение y. Мы не сильно удивлены, если выход нами ожидаем, и сильно удивлены, если выход неожиданный. Конечно, я не давал строгого определения «удивлению», поэтому всё это можно показаться пустым разглагольствованием. Но на самом деле в теории информации существует точный способ определения неожиданности. К сожалению, мне неизвестно ни одного примера хорошего, короткого и самодостаточного обсуждения этого момента в интернете. Но если вам интересно копнуть поглубже, то в статье в Википедии есть хорошая общая информация, которая отправит вас в нужном направлении. Детали можно почерпнуть из 5-й главы, касающейся неравенства Крафта, в книжке по теории информации [англ.].

Задача

• Мы подробно обсудили замедление обучения, которое может произойти при насыщении нейронов в сетях с использованием квадратичной функции стоимости при обучении. Ещё один фактор, способный подавлять обучение – наличие члена x_j в уравнении (61). Из-за него, когда выход x_j приближается к нуля, соответствующий вес w_j будет обучаться медленно. Поясните, почему невозможно устранить член x_j выбором какой-нибудь хитроумной функции стоимости.

Softmax (функция мягкого максимума)

В данной главе мы по большей части будем использовать функцию стоимости с перекрёстной энтропией для решения проблем замедления обучения. Однако мне хочется кратко обсудить ещё один подход к этой проблеме, основанный на т.н. softmax-слоях нейронов. Мы не будем использовать Softmax-слои в оставшейся части главы, поэтому, если вы очень торопитесь, можете пропустить этот раздел. Однако в Softmax всё же стоит разобраться, в частности, потому, что она интересна сама по себе, и в частности потому, что мы будем использовать Softmax-слои в главе 6, в нашем обсуждении глубоких нейросетей.

Идея Softmax состоит в том, чтобы определить новый тип выходного слоя для НС. Он начинается так же, как сигмоидный слой, с формирования взвешенных входов $$. Однако мы не применяем сигмоиду для получения ответа. В Softmax-слое мы применяем Softmax-функцию к z^L_j. Согласно ей, активация a^L_j выходного нейрона №j равна:

$$

где в знаменателе мы суммируем по всем выходным нейронам.

Если Softmax-функция вам незнакома, уравнение (78) покажется вам загадочным. Совершенно неочевидно, зачем нам использовать такую функцию. Также неочевидно, что она поможет нам решить проблему замедления обучения. Чтобы лучше понять уравнение (78), предположим, что у нас есть сеть с четырьмя выходными нейронами и четырьмя соответствующими взвешенными входами, которые мы будем обозначать, как z^L₁, z^L₂, z^L₃ и z^L₄. В оригинале статьи имеются интерактивные регулировочные ползунки, которым назначены возможные значения взвешенных входов и график соответствующих выходных активаций. Хорошей отправной точкой для их изучения будет использование нижнего ползунка для увеличения z^L₄.





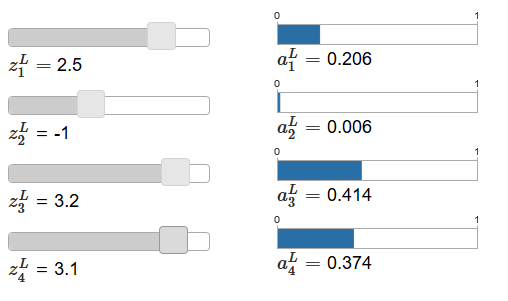
Увеличивая z^L₄, можно наблюдать увеличение соответствующей выходной активации, a^L₄, и уменьшение остальных выходных активаций. При уменьшении z^L₄ a^L₄ будет уменьшаться, а все остальные выходные активации – увеличиваться. Присмотревшись, вы увидите, что в обоих случаях общее изменение других активаций точно компенсирует изменение, происходящее в a^L₄. Причина этого в наличии гарантии того, что все выходные активации в сумме дают 1, что мы можем доказать при помощи уравнения (78) и кое-какой алгебры:

$$

В итоге, с увеличением a^L₄ остальные выходные активации обязаны уменьшаться на то же значение в сумме, чтобы гарантировать, что сумма всех выходных активаций будет равной 1. И, конечно, сходные утверждения будут верны для всех остальных активаций.

Из уравнения (78) также следует, что все выходные активации положительны, поскольку функция экспоненты положительна. Сочетая это с наблюдением из предыдущего параграфа, получим, что выход Softmax-слоя будет набором положительных чисел, дающих в сумме 1. Иначе говоря, выход Softmax-слоя можно представить, как распределение вероятности.

То, что выход Softmax-слоя – это распределение вероятности, весьма приятно. Во многих задачах удобно иметь возможность интерпретировать выходные активации a^L_j как оценку сетью вероятности того, что правильным вариантом булет j. Так что, к примеру в задаче классификации MNIST мы можем интерпретировать a^L_j как оценку сетью вероятности того, что правильным вариантом классификации цифры будет j.

И наоборот, если выходной слой был сигмоидным, тогда мы определённо не можем предполагать, что активации формируют распределение вероятности. Я не буду доказывать это строго, но разумно считать, что активации сигмоидного слоя в общем случае не формируют распределение вероятности. Поэтому с использованием сигмоидного выходного слоя мы не получим такой простой интерпретации выходных активаций.

Упражнение

• Составьте пример, показывающий, что в сети с сигмоидным выходным слоем выходные активации a^L_j не всегда в сумме дают 1.

Мы начинаем немного разбираться в Softmax-функции и том, как ведут себя Softmax-слои. Просто чтобы подвести промежуточный итог: экспоненты в уравнении (78) гарантируют, что все выходные активации будут положительными. Сумма в знаменателе уравнения (78) гарантирует, что выход Softmax в сумме даст 1. Поэтому этот вид уравнения уже не кажется загадочным: это естественный способ гарантировать, чтобы выходные активации формировали распределение вероятности. Softmax можно представить себе, как способ изменения масштаба z^L_j с последующим сжатием их в кучку для формирования распределения вероятности.

Упражнения

• Монотонность Softmax. Покажите, что ∂a^L_j / ∂z^L_k положительна, если j=k, и отрицательна, если j≠k. Как следствие, увеличение z^L_j гарантированно увеличивает соответствующую выходную активацию a^L_j, и уменьшает все остальные выходные активации. Мы уже видели это эмпирически на примере ползунков, однако данное доказательство будет строгим.
• Нелокальность Softmax. Приятной особенностью сигмоидных слоёв является то, что выход a^L_j — функция соответствующего взвешенного входа, a^L_j = σ(z^L_j). Поясните, почему с Softmax-слоем это не так: любая выходная активация a^L_j зависит от всех взвешенных входов.

Задача

• Инвертирование Softmax-слоя. Допустим, у нас есть НС с выходным Softmax-слоем и активации a^L_j известны. Покажите, что соответствующие взвешенные входы имеют форму z^L_j = ln a^L_j + C, где C – константа, не зависящая от j.

Проблема замедления обучения

Мы уже достаточно близко познакомились с Softmax-слоями нейронов. Но пока что мы не видели, как Softmax-слои позволяют нам решить проблему замедления обучения. Чтобы понять это, давайте определим функцию стоимости на основе «логарифм-правдоподобия». Мы будем использовать x для обозначения обучающего входа сети, и y для соответствующего желаемого выхода. Тогда ЛПС, связанная с этим обучающим входом, будет:

$$

Так что, если мы, к примеру, обучаемся на изображениях MNIST, и на вход пошло изображение 7, тогда ЛПС будет равной −ln a^L₇. Чтобы понять это интуитивно, рассмотрим случай, когда сеть хорошо справляется с распознаванием, то есть, уверена, что на входе 7. В этом случае она оценит значение соответствующей вероятности a^L₇ как близкое к 1, поэтому стоимость −ln a^L₇ будет малой. И наоборот, если сеть работает плохо, то вероятность a^L₇ будет меньше, а стоимость −ln a^L₇ будет больше. Поэтому ЛПС ведёт себя так, как можно ожидать от функции стоимости.

Что насчёт проблемы замедления обучения? Для её анализа вспомним, что главное в замедлении – поведение величин ∂C/∂w^L_jk и ∂C/∂b^L_j. Не буду подробно расписывать взятие производной – попрошу вас сделать это в задачах, но с применением кое-какой алгебры можно показать, что:

$$

$$

Я тут немного поиграл с обозначениями, и использую «y» немного не так, как в прошлом параграфе. Там y обозначало желаемый выход сети – то есть, если на выходе «7», то на входе было изображение 7. А в этих уравнениях y обозначает вектор выходных активаций, соответствующий 7, то есть вектор, у которого все нули, кроме единички в 7-й позиции.

Эти уравнения такие же, как и аналогичные выражения, полученные нами в более раннем анализе перекрёстной энтропии. Сравните, к примеру, уравнения (82) и (67). Это то же уравнение, хотя в последнем проведено усреднение по обучающим примерам. И, как и в первом случае, эти выражения гарантируют отсутствие замедления обучения. Полезно представлять себе, что выходной Softmax-слой с ЛПС довольно сильно похожи на слой с сигмоидным выходом и стоимостью на основе перекрёстной энтропии.

Учитывая их схожесть, что нужно использовать – сигмоидный выход и перекрёстную энтропию, или Softmax-выход и ЛПС? На самом деле, во многих случаях хорошо работают оба подхода. Хотя далее в этой главе мы будем использовать сигмоидный выходной слой со стоимостью на основе перекрёстной энтропии. Позже, в главе 6, мы иногда будем использовать Softmax-выход и ЛПС. Причина изменений – сделать некоторые из следующих сетей более похожими на сети, встречающиеся в некоторых влиятельных научных работах. С более общей точки зрения, Softmax и ЛПС стоит использовать, когда вам нужно интерпретировать выходные активации как вероятности. Такое нужно не всегда, но может оказаться полезным в задачах классификации (типа MNIST), куда входят не пересекающиеся классы.

Задачи

• Выведите уравнения (81) и (82).
• Откуда взялось название Softmax? Допустим, мы изменим Softmax-функцию так, чтобы выходные активации задавались уравнением

  $$

  где c – положительная константа. Отметим, что c = 1 соответствует стандартной Softmax-функции. Но используя другое значение c, мы получим другую функцию, которая качественно всё равно будет похожей на Softmax. Покажите, что выходные активации формируют распределение вероятности, как и в случае с обычной Softmax. Допустим, мы сделаем c очень большой, то есть c → &inf;. Какого ограничивающее значение выходных активаций a^L_j? После решения этой задачи должно быть ясно, почему функция с c = 1 считается «смягчённой версией» функции максимума. Отсюда и происходит термин softmax.
• Обратное распространение с Softmax и ЛПС. В прошлой главе мы вывели алгоритм обратного распространения для сети, содержащей сигмоидные слои. Чтобы применить этот алгоритм к сети и Softmax-слоями, нам надо вывести выражение для ошибки δ^L_j ≡ ∂C/∂z^L_j. Покажите, что подходящим выражением будет

  $$

  Исползуя это выражение, мы можем применить алгоритм обратного распространения к сети, используя выходной Softmax-слой и ЛПС.

Переобучение и регуляризация

У нобелевского лауреата Энрико Ферми как-то спросили мнение по поводу математической модели, предложенной несколькими коллегами для решения важной нерешённой физической проблемы. Модель прекрасно соответствовала эксперименту, но Ферми отнёсся к ней скептически. Он спросил, сколько свободных параметров в ней можно менять. «Четыре», — сказали ему. Ферми ответил: «Помню, как мой друг Джонни фон Нейман любил говорить, что с четырьмя параметрами туда можно запихнуть и слона, а с пятью можно заставить его махать хоботом».

Смысл истории, конечно, в том, что модели с большим количеством свободных параметров могут описывать удивительно широкий круг явлений. Даже если такая модель хорошо работает с доступными данными, это не делает её автоматически хорошей моделью. Это просто может означать, что у модели достаточно свободы, чтобы она могла описать почти любой набор данных заданного размера, не выявляя основной идеи явления. Когда это происходит, модель хорошо работает с существующими данными, но не сможет обобщить новую ситуацию. Истинная проверка модели – её способность делать предсказания в ситуациях, с которыми она не сталкивалась ранее.

Ферми и фон Нейман подозрительно относились к моделям с четырьмя параметрами. У нашей НС с 30 скрытыми нейронами для классификации цифр MNIST есть почти 24 000 параметров! Это довольно много параметров. У нашей НС с 100 скрытыми нейронами есть почти 80 000 параметров, а у передовых глубоких НС этих параметров иногда миллионы или даже миллиарды. Можем ли мы доверять результатам их работы?

Давайте усложним эту проблему, создав ситуацию, в которой наша сеть плохо обобщает новую для неё ситуацию. Мы будем использовать НС с 30 скрытыми нейронами и 23 860 параметрами. Но мы не будем обучать сеть при помощи всех 50 000 изображений MNIST. Вместо этого используем только первые 1000. Использование ограниченного набора сделает проблему обобщения более очевидной. Мы будем обучаться так, как и раньше, используя функцию стоимости на основе перекрёстной энтропии, со скоростью обучения η=0,5 и размером мини-пакета 10. Однако мы будем обучаться 400 эпох, что немного больше, чем было раньше, поскольку обучающих примеров у нас не так много. Давайте используем network2, чтобы посмотреть на то, как меняется функция стоимости:

>>> import mnist_loader 
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2 
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) 
>>> net.large_weight_initializer()
>>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data,
... monitor_evaluation_accuracy=True, monitor_training_cost=True)

Используя результаты, мы можем построить график изменения стоимости при обучении сети (графики сделаны при помощи программы overfitting.py):



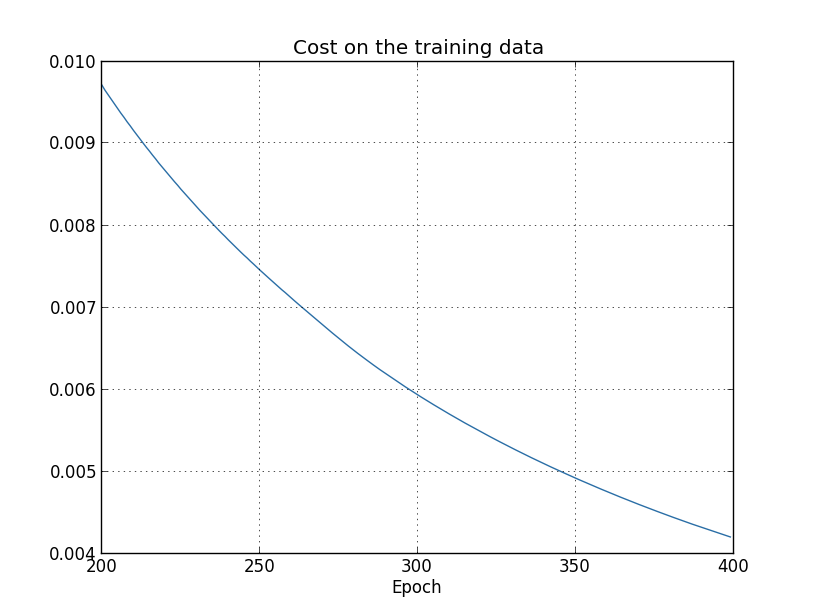
Выглядит обнадёживающе, идёт гладкое уменьшение стоимости, как и ожидалось. Учтите, что я показал только эпохи с 200 по 399. В итоге мы видим в увеличенном масштаба поздние этапы обучения, на которых, как мы увидим далее, и происходит всё самое интересное.

Теперь посмотрим, как меняется точность классификации на проверочных данных во времени:



Тут я снова увеличил график. В первые 200 эпох, которых тут не видно, точность растёт почти до 82%. Затем обучение постепенно замедляется. Наконец, примерно на 280-й эпохе точность классификации перестаёт улучшаться. На поздних эпохах наблюдаются лишь небольшие стохастические флуктуации вокруг значения точности, достигнутого на 280-й эпохе. Сравните это с предыдущим графиком, где стоимость, связанная с обучающими данными, плавно уменьшается. Если изучать только эту стоимость, то будет казаться, что модель улучшается. Однако результаты работы с проверочными данными говорят нам, что это улучшение – лишь иллюзия. Как и в модели, которая не понравилась Ферми, то, что наша сеть изучает после 280-й эпохи, уже не обобщается на проверочных данных. Поэтому это обучение перестаёт быть полезным. Мы говорим, что после 280-й эпохи сеть переобучается, или переподгоняется [overfitting or overtraining].

Вы можете задуматься над тем, не является ли проблемой то, что я изучаю стоимость на основе обучающих данных, а не точности классификации проверочных данных. Иначе говоря, возможно, проблема в том, что мы сравниваем яблоки с апельсинами. Что будет, если мы сравним стоимость обучающих данных со стоимостью проверочных, то есть, будем сравнивать сравнимые меры? Или, возможно, мы могли бы сравнить точность классификации как обучающих, так и проверочных данных? На самом деле, то же явление проявляется вне зависимости от того, как проводить сравнение. Но изменяются детали. К примеру, давайте посмотрим стоимость проверочных данных:



Видно, что стоимость проверочных данных улучшается примерно до 15-й эпохи, а потом вообще начинает ухудшаться, хотя стоимость обучающих данных продолжает улучшаться. Это ещё один признак переобученной модели. Однако встаёт вопрос, какую эпоху мы должны считать точкой, в которой переобучение начинает преобладать над обучением – 15 или 280? С практической точки зрения нас всё же интересует улучшение точности классификации проверочных данных, а стоимость – это всего лишь посредник точности классификации. Поэтому имеет смысл считать эпоху 280 точкой, после которой переобучение начинает преобладать над обучением нашей НС.

Ещё один признак переобучения можно увидеть в точности классификации обучающих данных:



Точность растёт, доходя до 100%. То есть, наша сеть правильно классифицирует все 1000 обучающих изображений! Тем временем, проверочная точность вырастает лишь до 82,27%. То есть, наша сеть лишь изучает особенности обучающего набора, а не учится распознавать цифры вообще. Похоже на то, что сеть просто запоминает обучающий набор, недостаточно хорошо поняв цифры для того, чтобы обобщить это на проверочный набор.

Переобучение – серьёзная проблема НС. Особенно это верно для современных НС, в которых обычно есть огромное количество весов и смещений. Для эффективного обучения нам нужен способ определять, когда возникает переобучение, чтобы не переобучать. А ещё нам хотелось бы уметь уменьшать эффекты переобучения.

Очевидный способ обнаружить переобучение – использовать подход выше, следить за точностью работы с проверочными данными в процессе обучения сети. Если мы увидим, что точность на проверочных данных уже не улучшается, надо прекращать обучение. Конечно, строго говоря, это не обязательно будет признаком переобучения. Возможно, точность работы с проверочными и с обучающими данными прекратят улучшаться одновременно. И всё же применение такой стратегии предотвратит переобучение.

А мы будем использовать небольшую вариацию этой стратегии. Вспомним, что когда мы загружаем в MNIST данные, мы делим их на три набора:

>>> import mnist_loader 
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()

Пока что мы использовали training_data и test_data, и игнорировали validation_data [подтверждающие]. В validation_data содержится 10 000 изображений, отличающихся как от 50 000 изображений обучающего набора MNIST, так и от 10 000 изображений проверочного набора. Вместо использования test_data для предотвращения переобучения мы будем использовать validation_data. Для этого мы будем использовать практически ту же стратегию, что была описана выше для test_data. То есть, мы будем вычислять точность классификации validation_data в конце каждой эпохи. Как только точность классификации validation_data насытится, мы перестанем обучаться. Эта стратегия называется ранней остановкой. Конечно, на практике мы не сможем сразу же узнать, что точность насытилась. Вместо этого мы будем продолжать обучение, пока не удостоверимся в этом (причём решить, когда нужно остановиться, не всегда просто, и можно использовать для этого более или менее агрессивные подходы).

Зачем использовать validation_data для предотвращения переобучения, а не test_data? Это часть более общей стратегии – использовать validation_data для оценки разных вариантов выбора гиперпараметров – количества эпох для обучения, скорости обучения, наилучшей архитектуры сети, и т.д. Эти оценки мы используем, чтобы найти и присвоить хорошие значения гиперпараметрам. И хотя я пока ещё этого не упоминал, частично благодаря этому я и сделал выбор гиперпараметров в ранних примерах в книге.

Конечно, это замечание не отвечает на вопрос о том, почему мы используем validation_data, а не test_data, для предотвращения переобучения. Оно просто заменяет ответ на более общий вопрос – почему мы используем validation_data, а не test_data, для выбора гиперпараметров? Чтобы понять это, учтите, что при выборе гиперпараметров нам, скорее всего, придётся выбирать из множества их вариантов. Если мы будем назначать гиперпараметры на основе оценок из test_data, мы, возможно, слишком сильно подгоним эти данные именно под test_data. То есть, мы, возможно, найдём гиперпараметры, хорошо подходящие под особенности конкретных данных из test_data, однако работа нашей сети не будет обобщаться на другие наборы данных. Этого мы избегаем, подбирая гиперпараметры при помощи validation_data. А потом, получив нужные нам ГП, мы проводим итоговую оценку точности с использованием test_data. Это даёт нам уверенность в том, что наши результаты работы с test_data являются истинной мерой степени генерализации НС. Иначе говоря, подтверждающие данные – это такие особые обучающие данные, помогающие нам обучиться хорошим ГП. Такой подход к поиску ГП иногда называют методом удержания, поскольку validation_data «удерживают» отдельно от training_data.

На практике, даже после оценки качества работы на test_data мы захотим поменять наше мнение и попробовать другой подход – возможно, другую архитектуру сети – который будет включать поиски нового набора ГП. В этом случае не возникнет ли опасность того, что мы излишне приспособимся к test_data? Не потребуется ли нам потенциально бесконечное количество наборов данных, чтобы мы были уверены в том, что наши результаты хорошо обобщаются? В целом это глубокая и сложная проблема. Но для наших практических целей мы не будем слишком сильно переживать по этому поводу. Мы просто нырнём с головой в дальнейшие исследования, используя простой метод удержания на основе training_data, validation_data и test_data, как описано выше.

Пока что мы рассматривали переобучение с использованием 1000 обучающих изображений. Что будет, если мы используем полный обучающий набор из 50 000 изображений? Все остальные параметры мы оставим без изменений (30 скрытых нейронов, скорость обучения 0,5, размер мини-пакета 10), но будем обучаться 30 эпох с использованием всех 50 000 картинок. Вот график, на котором показана точность классификации на обучающих данных и проверочных данных. Отметьте, что здесь я использовал проверочные [test], а не подтверждающие [validation] данные, чтобы результаты было проще сравнивать с более ранними графиками.



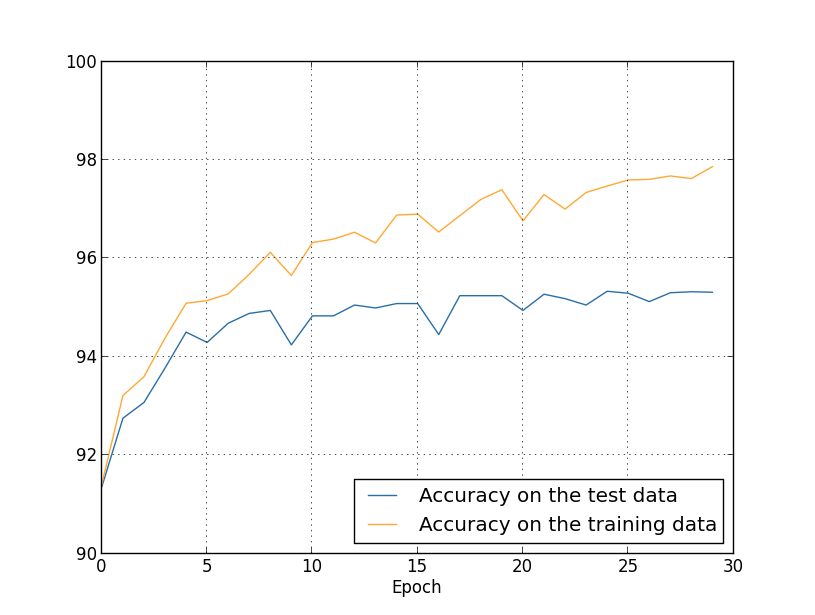
Видно, что показатели точности на проверочных и обучающих данных остаются ближе друг к другу, чем при использовании 1000 обучающих примеров. В частности, наилучшая точность классификации, 97,86%, всего на 2,53% выше, чем 95,33% проверочных данных. Сравните с ранним разрывом в 17,73%! Переобучение происходит, но сильно уменьшилось. Наша сеть гораздо лучше обобщает информацию, переходя с обучающих на проверочные данные. В целом, один из лучших способов уменьшения переобучения — увеличение объёма обучающих данных. Взяв достаточно обучающих данных, сложно переобучить даже очень крупную сеть. К сожалению, получить обучающие данные бывает дорого и/или сложно, поэтому такой вариант не всегда оказывается практичным.

Регуляризация

Увеличение количества обучающих данных – один из способов уменьшения переобучения. Есть ли другие способы уменьшения проявлений переобучения? Один из возможных подходов – уменьшение размера сети. Правда, у больших сетей возможностей потенциально больше чем у малых, поэтому к такому варианту мы прибегаем неохотно.

К счастью, существуют и другие техники, способные уменьшить переобучение, даже когда у нас фиксированы размер сети и обучающих данных. Они известны, как техники регуляризации. В данной главе я опишу одну из наиболее популярных техник, которую иногда называют ослаблением весов, или регуляризацией L2. Её идея в том, чтобы добавить к функции стоимости дополнительный член под названием член регуляризации. Вот перекрёстная энтропия с регуляризацией:

$$

Первый член – обычное выражение для перекрёстной энтропии. Но мы добавили второй, а именно, сумму квадратов всех весов сети. Он масштабируется множителем λ/2n, где λ>0 – это параметр регуляризации, а n, как обычно – размер обучающего набора. Мы обсудим, как выбрать λ. Также стоит отметить, что в член регуляризации не входят смещения. Об этом ниже.

Конечно, возможно регуляризировать и другие функции стоимости, например, квадратичную. Это можно сделать схожим образом:

$$

В обоих случаях можно записать регуляризированную функцию стоимости, как

$$

где C₀ — оригинальная функция стоимости без регуляризации.

Интуитивно ясно, что смысл регуляризации склонить сеть к предпочтению более малых весов, при прочих равных. Крупные веса будут возможны, только если они значительно улучшают первую часть функции стоимости. Иначе говоря, регуляризация – это способ выбора компромисса между нахождением малых весов и минимизацией изначальной функции стоимости. Важно, что эти два элемента компромисса зависят от значения λ: когда λ мала, мы предпочитаем минимизировать оригинальную функцию стоимости, а когда λ велика, то предпочитаем малые веса.

Совершенно не очевидно, почему выбор подобного компромисса должен помочь уменьшить переобучение! Но оказывается, помогает. Мы разберёмся в том, почему он помогает, в следующей секции. Но сначала давайте поработаем с примером, показывающим, что регуляризация действительно уменьшает переобучение.

Чтобы сконструировать пример, сначала нам нужно понять, как применить обучающий алгоритм со стохастическим градиентным спуском к регуляризованной НС. В частности, нам надо знать, как подсчитывать частные производные, ∂C/∂w и ∂C/∂b для всех весов и смещений в сети. После взятия частных производных в уравнении (87) получим:

$$

$$

Члены ∂C₀/∂w и ∂C₀/∂w можно вычислить через ОР, как описано в предыдущей главе. Мы видим, что подсчитать градиент регуляризованной функции стоимости легко: просто нужно, как обычно, использовать ОР, а потом добавить λ/n w к частной производной всех весовых членов. Частные производные по смещениям не меняются, поэтому правило обучения градиентным спуском для смещений не отличается от обычного:

$$

Правило обучения для весов превращается в:

$$

$$

Всё то же самое, что и в обычном правиле градиентного спуска, кроме того, что мы сначала масштабируем вес w на множитель 1 — ηλ/n. Это масштабирование иногда называют ослаблением весов, поскольку оно уменьшает веса. На первый вщгляд кажется, что веса неудержимо стремятся к нулю. Но это не так, поскольку другой член может привести к увеличению весов, если это приводит к уменьшению нерегуляризованной функции стоимости.

Хорошо, пусть градиентный спуск работает так. Что насчёт стохастического градиентного спуска? Ну, как и в нерегуляризованном варианте стохастического градиентного спуска, мы можем оценить ∂C₀/∂w через усреднение по мини-пакету m обучающих примеров. Поэтому регуляризованное правило обучения для стохастического градиентного спуска превращается в (см. уравнение (20)):

$$

где сумма идёт по обучающим примерам x в мини-пакете, а C_x — нерегуляризованная стоимость для каждого обучающего примера. Всё то же самое, что и в обычно правиле стохастического градиентного спуска, за исключением 1 — ηλ/n, фактора ослабления веса. Наконец, для полноты картины, позвольте записать регуляризованное правило для смещений. Оно, естественно, точно такое же, как и в нерегуляризованном случае (см. уравнение (21)):

$$

где сумма идёт по обучающим примерам x в мини-пакете.

Давайте посмотрим, как регуляризация меняет эффективность нашей НС. Мы будем использовать сеть с 30 скрытыми нейронами, мини-пакет размера 10, скорость обучения 0,5, и функцию стоимости с перекрёстной энтропией. Однако на этот раз мы исполоьзуем параметр регуляризации λ=0,1. В коде я назвал эту переменную lmbda, поскольку слово lambda зарезервировано в python для не связанных с нашей темой вещей. Я также снова использовал test_data again вместо validation_data. Но я решил использовать test_data, поскольку результаты можно сравнивать напрямую с нашими ранними, нерегуляризованными результатами. Вы легко можете поменять код так, чтобы он использовал validation_data, и убедиться, что результаты получаются схожими.

>>> import mnist_loader 
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper() 
>>> import network2 
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data[:1000], 400, 10, 0.5,
... evaluation_data=test_data, lmbda = 0.1,
... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True,
... monitor_training_cost=True, monitor_training_accuracy=True)

Стоимость обучающих данных постоянно уменьшается, как и раннем случае, без регуляризации:



Но на этот раз точность на test_data продолжает увеличиваться в течение всех 400 эпох:



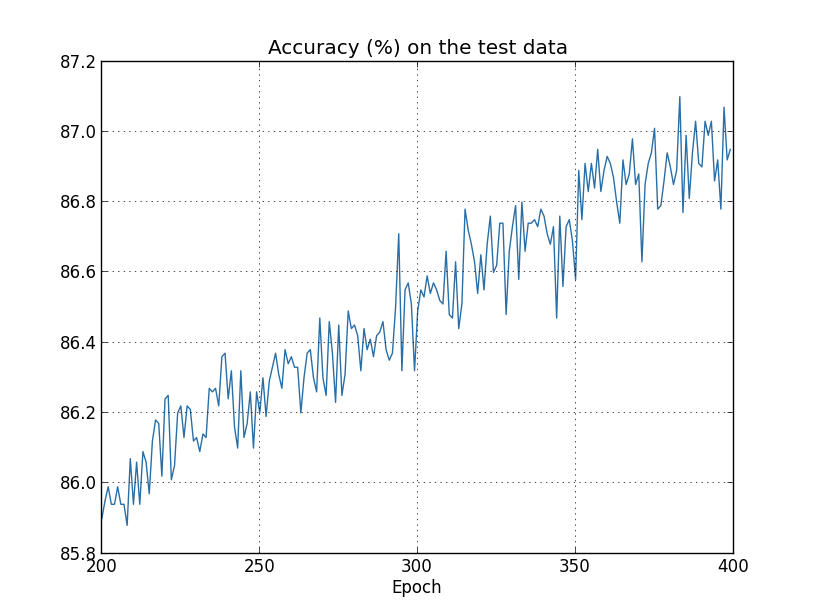
Очевидно, регуляризация подавила переобучение. Более того, точность значительно возросла, и пиковая точность классификации достигает 87,1%, по сравнению с пиком 82,27%, достигнутым в случае без регуляризации. И вообще, мы почти наверняка достигаем лучших результатов, продолжая обучение после 400 эпох. Судя по всему, эмпирически, регуляризация заставляет нашу сеть лучше обобщать знания, и значительно уменьшает эффекты переобучения.

Что произойдёт, если мы оставим наше искусственное окружение, в котором используется всего 1 000 обучающих картинок, и вернёмся к полному набору из 50 000 изображений? Конечно, мы уже увидели, что переобучение представляет куда как меньшую проблему с полным набором из 50 000 изображений. Помогает ли улучшить результат регуляризация? Давайте оставим прежние значения гиперпараметров – 30 эпох, скорость 0,5, размер мини-пакета 10. Однако, нам нужно поменять параметр регуляризации. Дело в том, что размер n обучающего набора скакнул от 1000 до 50 000, а это меняет фактор ослабления весов 1 — ηλ/n. Если мы продолжим использовать λ=0,1, это означало бы, что веса ослабляются куда меньше, и в итоге эффект от регуляризации уменьшается. Мы компенсируем это, приняв λ=5,0.

Хорошо, давайте обучим нашу сеть, сначала повторно инициализировав веса:

>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5,
... evaluation_data=test_data, lmbda = 5.0,
... monitor_evaluation_accuracy=True, monitor_training_accuracy=True)

Мы получаем результаты:



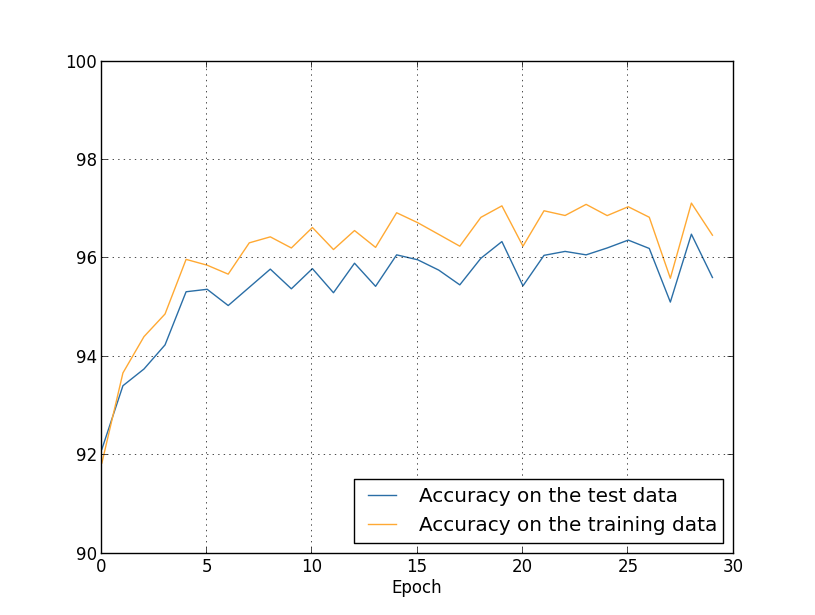
Много всего приятного. Во-первых, наша точность классификации на проверочных данных подросла, с 95,49% без регуляризации до 96,49% с регуляризацией. Это серьёзное улучшение. Во-вторых, можно видеть, что разрыв между результатами работы на обучающем и проверочном наборах гораздо ниже, чем раньше, менее 1%. Разрыв всё равно приличный, но мы, очевидно, достигли значительного прогресса в уменьшении переобучения.

Наконец, посмотри, какую точность классификации мы получим при использовании 100 скрытых нейронов и параметра регуляризации &lambda=5,0. Не буду приводить подробный анализ переобучения, это делается просто ради интереса, чтобы посмотреть, насколько большой точности можно достигнуть с нашими новыми хитростями: функцией стоимости с перекрёстной энтропией и регуляризацией L2.

>>> net = network2.Network([784, 100, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5, lmbda=5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True)

Конечный результат – точность классификации в 97,92% на подтверждающих данных. Большой скачок по сравнению со случаем с 30 скрытыми нейронами. Можно подстроить ещё немного, запустить процесс на 60 эпох с η=0,1 и λ=5,0, и преодолеть барьер в 98%, достигнув точность 98,04 на подтверждающих данных. Неплохо для 152 строк кода!

Я описал регуляризацию как способ уменьшения переобучения и увеличения точности классификации. Но это не единственные её преимущества. Эмпирически, испробовав через множество запусков нашу сеть MNIST, меняя каждый раз веса, я обнаружил, что запуски без регуляризации иногда «застревали», очевидно, попав в локальный минимум функции стоимости. В итоге разные запуски иногда выдавали сильно разные результаты. А регуляризация, наоборот, позволяет получать гораздо легче воспроизводимые результаты.

Почему так получается? Эвристически, когда у функции стоимости нет регуляризации, длина вектора весов, скорее всего, будет расти, при прочих равных. Со временем это может привести к очень большому вектору весов. А из-за этого вектор весов может застрять, показывая примерно в одном и том же направлении, поскольку изменения из-за градиентного спуска делают лишь крохотные изменения в направлении при большой длине вектора. Я считаю, что из-за этого явления нашему алгоритму обучения очень тяжело как следует изучить пространство весов, и, следовательно, тяжело найти хороший минимум функции стоимости.