Нейронные сети в борьбе с раком
- суббота, 8 апреля 2017 г. в 03:14:23

В прошлом году мы с Артуром Кадуриным решили присоединиться к новой волне обучения нейронных сетей — к глубокому обучению. Сразу стало ясно, что машинное обучение во многих сферах практически не используется, а мы в свою очередь понимаем как его можно применить. Оставалось найти интересную область и сильных экспертов в ней. Так мы и познакомились с командой из Insilico Medicine (резидент БМТ-кластера фонда «Сколково») и разработчиками из МФТИ и решили вместе поработать над задачей поиска лекарств против рака.
Ниже вы прочитаете обзор статьи The cornucopia of meaningful leads: Applying deep adversarial autoencoders for new molecule development in oncology, которую мы с коллегами из Insilico Medicine и МФТИ подготовили для американского журнала Oncotarget, с упором на реализацию предложенной модели во фреймворке tensorflow. Исходная задача была следующей. Есть данные вида: вещество, концентрация, показатель роста раковых клеток. Нужно сгенерировать новые вещества, которые останавливали бы рост опухоли при определенной концентрации. Датасет доступен на сайте NCI Wiki.
Давайте более подробно опишем данные.
Вещества представлены в стандартном для биоинформатики виде — SMILES, фактически это унифицированный способ записи соединений в ASCII. К сожалению, здесь нет полной унификации, разные пакеты генерируют разные SMILES. Мы пользовались теми, что созданы с помощью пакета CACTVS. Подробнее об этом написано, например, тут. Каждый SMILES можно перевести в бинарное представление размерности 166: Molecular ACCess System (MACCS) chemical fingerprint. Каждый бит в этом представлении — ответ на вопрос о соответствующей молекуле, MACCS keys — набор соответствующих вопросов. Примеры вопросов: в молекуле меньше трех атомов кислорода? Есть ли в молекуле кольцо размера три? Более подробное описание — здесь.
Индекс роста определяется следующим образом:
где — начальный размер опухоли, — размер опухоли через какой-то интервал времени в присутствии препарата, — размер опухоли в контрольной группе без добавления препарата. Фактически показывает, насколько медленнее растет опухоль или как быстро она уменьшается.
После описанной обработки получается 78 728 троек вида fingerprint, log(concentration), GI, описывающие 6252 молекулы. Для валидации модели мы использовали бинарные представления почти для 100 миллионов молекул из базы Pubchem (The PubChem Project).
Пример полученных исходных данных:
| Fingerprint | Log(concentration) | Growth inhibition percentage |
|---|---|---|
| 000011100010... | –5 | 10 % |
| 00000110101… | –7 | –15 % |
| 10010011000… | –4,8 | 75 % |
Первый приходящий в голову подход: обучить регрессор (например, xgboost) определять по двойке вида fingerprint, log(concentration) показатель роста, а дальше семплировать такие двойки из большой базы и выделять лучшие.

Мы не смогли довести такой подход до чего-либо хорошего.
Другой вариант: научиться генерировать пары (fingerprint, концентрация) и дальше искать похожие молекулы из большой базы соединений. Один из первых вопросов: как сравнивать разные молекулы? К счастью (?), опытным путем выяснили, что в данном случае можно использовать меру Жаккара, причем для многих приложений молекулы с коэффициентом Жаккара больше 0,8 уже считаются близкими.
Кроме решения задачи как таковой мы преследовали цель научиться использовать новые генеративные нейросетевые подходы. Известны две современных генеративных модели — VAE (variational autoencoder) и GAN (generative adversarial encoder). Так как обе модели уже несколько раз были описаны на Хабре, ограничимся небольшим рассказом о них.
В случае VAE решается задача приближения в виде
где — входные данные, — латентное представление, а — параметры модели.
Стандартный VAE предполагает, что распределения и нормальные, и приближает с помощью нейронной сети со структурой autoencoder.
Входные данные подаются на вход энкодеру, на выходе которого получается нормальное распределение . Далее из этого распределения семплируется вектор , который, в свою очередь, подается на вход декодеру. На выходе — вектор , реконструкция вектора .
При обучении нейронной сети оптимизируется среднее между двумя функциями потерь: KL divergence между распределением на латентном слое и и ошибка реконструкции — расстояние между и .
В случае GAN обучаются две нейронных сети: генератор и дискриминатор. Генератор переводит латентную переменную , семплированную из приорного распределения , в пространство входных данных, а дискриминатор учится отличать семплированные данные от настоящих. Задачу можно сформулировать в теоретико-игровой форме:

Наконец, в статье Adversarial Autoencoders вводится смесь моделей VAE и GAN. Так же, как и в обычном AE, вход подается в энкодер, выход которого , в свою очередь, попадает на вход декодеру. Сеть-дискриминатор учится различать вектор , семплированный из , и вектор . Как и в GAN, оптимизируются две функции потерь:
При этом вводится дополнительная функция потерь — ошибка реконструкции. Оптимизация по функциям потерь происходит поочередно. Например, первый цикл обучения будет выглядеть следующим образом: обучить дискриминатор на мини-батче, обучить энкодер на следующем мини-батче и обучить автоэнкодер на третьем мини-батче.

Модели VAE и GAN в последнее время особенно популярны в задачах генерации изображений, причем модели, основанные на GAN, на практике показывают себя лучше (например, NIPS 2016 Tutorial: Generative Adversarial Networks).
По этой причине и из-за простоты добавления индекса роста в латентный слой автоэнкодера мы остановились на последнем подходе для решения конкретной задачи (ждем публикации нашей новой статьи с детальным сравнением разных моделей). К тому же в решении задачи мы так и не смогли найти гиперпараметры стандартной архитектуры GAN, с которыми она бы стабильно работала.
Модель, к которой мы пришли, выглядит следующим образом:
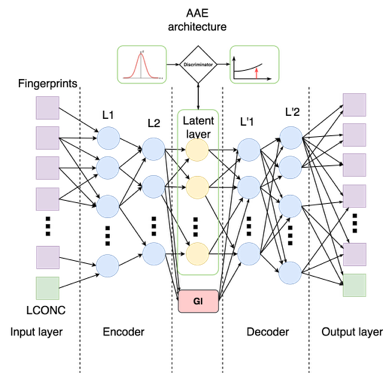
Для того чтобы концентрация как можно меньше влияла на выход энкодера, мы добавили еще одну функцию потерь — manifold loss:
где — энкодер, а — косинусная мера.
Наконец, в латентном слое мы решаем задачу регрессии: по латентному представлению фингерпринта и концентрации определить , добавив соответствующую функцию потерь. В итоге каждый шаг обучения состоит из пяти этапов:
Код всего процесса обучения лежит здесь (в данный момент мы продолжаем эксперименты с кодом и собираемся в ближайшем будущем выложить улучшенную версию).
Разберем подробнее реализацию архитектуры сети и метрики. Веса каждой части сети мы выделяем в отдельный tf.name_scope, чтобы иметь возможность их по отдельности оптимизировать. Дополнительно мы выделяем концентрацию из входного слоя в отдельную переменную и отдельно считаем для нее ошибку реконструкции.
Как обычно, сеть является последовательностью линейных слоев и функций активации. Например, энкодер устроен следующим образом (aae_v3.py, строки 109—127):
# Encoder net: 166+1->128->64->3+1
with tf.name_scope("encoder"):
encoder = [self.visible_tensor]
sizes = [self.input_space + 1, 128, 64, self.latent_space]
for layer_number in xrange(encoder_layers):
with tf.name_scope("encoder-%s" % layer_number):
enc_l = layer_output(sizes[layer_number], sizes[layer_number + 1], encoder[-1], 'enc_l')
encoder.append(enc_l)
with tf.name_scope("encoder-fp"):
self.encoded_fp = layer_output(sizes[-2], sizes[-1], encoder[-1], 'encoded_fp', batch_normed=False, activation_function=identity_function)
with tf.name_scope("tgi-encoder"):
self.encoded_tgi = layer_output(sizes[-2], 1, encoder[-1], 'encoded_tgi', batch_normed=False, activation_function=identity_function)
self.encoded = tf.concat(1, [self.encoded_fp, self.encoded_tgi])Функция потерь дискриминатора:
Для борьбы с переполнением мы считаем сигмоиду не сразу на выходе дискриминатора, а прямо внутри функции потерь. В коде:
self.disc_loss = tf.reduce_mean(tf.nn.relu(self.disc_prior) - self.disc_prior + tf.log(1.0 +tf.exp(-tf.abs(self.disc_prior)))) + tf.reduce_mean(tf.nn.relu(self.disc_enc) + tf.log(1.0 + tf.exp(-tf.abs(self.disc_enc))))Функция потерь энкодера:
В коде:
self.enc_fp_loss = tf.reduce_mean(tf.nn.relu(self.disc_enc) - self.disc_enc + tf.log(1.0 + tf.exp(-tf.abs(self.disc_enc))))Функция потерь автоэнкодера:
В коде:
self.dec_fp_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(self.decoded_fp, self.fingerprint_tensor))
self.dec_conc_loss = tf.reduce_mean(tf.square(tf.sub(self.conc_tensor, self.decoded_conc)))
self.dec_loss = self.dec_fp_loss + self.dec_conc_lossРегрессор:
В коде:
self.enc_tgi_loss = tf.reduce_mean(tf.square(tf.sub(self.tgi_tensor, self.encoded_tgi)))Manifold loss в коде:
fp_norms = tf.sqrt(tf.reduce_sum(tf.square(self.encoded_fp), keep_dims=True, reduction_indices=[1]))
normalized_fp = tf.div(self.encoded_fp, fp_norms)
cosines_fp = tf.matmul(normalized_fp, tf.transpose(normalized_fp))
self.manifold_cost = tf.reduce_mean(1 - tf.boolean_mask(cosines_fp, self.targets_tensor))В наших экспериментах сеть с разными конфигурациями вела себя нестабильно. Чтобы увеличить стабильность перед основным процессом обучения, мы повторяли шаги 1, 2 и 5, пока дискриминатор и энкодер не пришли в состояние равновесия: discriminator_loss < 0,7 и encoder_loss < 0,7.
После обучения мы стандартным для GAN образом генерируем случайную выборку из 1000 пар (fingerprint, концентрация) с условием :
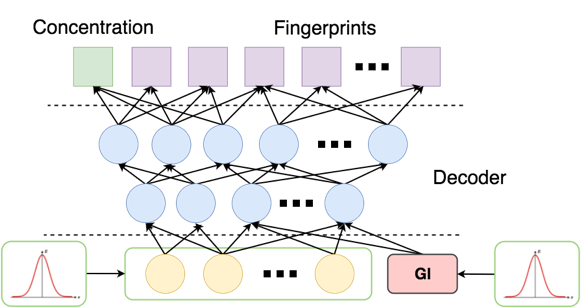
Подаем в латентный слой приорное распределение, а вместо — небольшие числа с нормальным шумом (нули подавать плохо, так как функция в этой точке имеет разрыв). На выходе мы получили 32 вектора вероятностей битов фингерпринта с концентрацией < –5.
Наконец, осталось найти настоящие молекулы из большой базы, похожие на полученные векторы. Есть как минимум три подхода:
По каждому вектору вероятностей мы нашли топ-10 «похожих» молекул для каждого из трех подходов и получили сходные результаты.
Как результат мы обнаружили 69 уникальных веществ, которых не было в обучающей выборке. По данным из базы The PubChem Project, примерно половина веществ либо уже применяется против рака, либо имеет доказанное действие против раковых опухолей. Мы ожидаем, что оставшаяся половина веществ также потенциально может бороться с раком.
Таким образом, достаточно наивный подход со сравнительно маленькими входными данными позволил получить хороший результат. Ожидается, что многие задачи биоинформатики можно будет решать похожими методами.
К сожалению, в каждом конкретном случае соперничающие сети ведут себя по-разному и при неверном выборе гиперпараметров сходятся к неправильным решениям (генератор побеждает дискриминатор, или наоборот). Мы работаем над тем, чтобы найти более стабильные структуры и методы обучения.