news.shamcode.ru | НеДождь. Модель для сборки. «Нервный Техник» #1 Аппарат для тренировки нейросети изгтовлен в кустарн

НеДождь. Модель для сборки. «Нервный Техник» #1 Аппарат для тренировки нейросети изгтовлен в кустарн

суббота, 7 декабря 2019 г. в 00:27:21

Python
Машинное обучение

Дорогой читатель!

Сегодня мы встречаемся не впервые: ушаты ~~помоев~~ объективной критики уже были вылиты хабровчанами на ранее выложенные мной наивные рассуждения об автоматической поэзии. Основными претензиями были «неприменимость этих рассуждений на практике» и «баян». Между строк читалась невероятная сложность, с которой, якобы, сопряжены манипуляции с машинным обучением. Пришло время показать, что всё намного проще, чем это принято считать.

«Мы не знаем, кем ты мечтаешь стать, наш читатель, — пилотом космического корабля, или исследователем тайн атомного ядра…

… Но одно твёрдо известно: даже если ты мечтаешь стать артистом, писателем, художником, то и тогда тебе всё равно необходимо знать основы машинного обучения»

(с) журнал «Юный Техник» №1 1956г. (нет)

Для самых маленьких:

Нефтью машинного обучения являются данные, которые, при «обучении с учителем» следует структурировать в однородные «таблицы» (массивы) — вход-выход, или иначе, задача-ответ. Такой набор принято называть Data Set. В университетах студентов тренируют на уже готовых дата сетах. Эти наборы можно собирать и самостоятельно. Программу для сбора информации называют парсер

Для матёрых:

Судя по комментариям, большинство хабровцев закончили МФТИ, а некоторые и не по одному разу. Это означает, что все уже знают кто именно «выжил на Титанике» и сколько стоила «однушка в Америке в 198х». Выход только один — самостоятельно собрать дата сет. Иначе пост будет смердеть баянами.

Определимся с задачей. В предложенном мной примере будем пытаться при помощи сети увеличить разрешение изображения. Соответственно, дата сет будет выглядеть как набор «плохая картинка»-«хорошая картинка».

Пример

Задача:

Ответ:

Разрешения у картинок бывают разные. Не все машины могут потянуть тяжёлые вычисления. Чтобы производительность и размеры картинок не стали ограничением, определим размеры наших картинок. задача 32х32 пикселей, ответ 64х64.

Пиксель (не всегда) — это сумма 3х чисел (см RGB), на выходе из парсера мы должны получить 2 массива с размерностями (N, 32, 32, 3) и (N, 64, 64, 3), где N — число примеров.

Далее предлагаю свои простые алгоритмы программ, и их не оптимальные, но работоспособные решения на Python:

Алгоритм парсера:

Из указанной директории берёт изображения высокого разрешения, делит их на небольшие квадраты, одновременно, уменьшая разрешение изображения вдвое, сохраняет в массивы оба варианта.

1 — с уменьшенным разрешением, 2 — с полным.

Сохраняет массивы на диск.
Вход: папка с фото
Выход: 2 файла содержащих дата сет x_train, y_train

Python код

import os
import pickle
import numpy as np
from PIL import Image as PLi
from tensorflow.keras.preprocessing import image as TFi

path = './source/'
temp_path = 'temp.bmp'
l = 64 
s = 32
x_train = []
y_train = []

def cut (image_path, coords):
    
    obj = PLi.open(image_path)
    cuted = obj.crop(coords)
    cuted.save(temp_path)  

    large = TFi.load_img(temp_path, target_size=(l,l))
    small = TFi.load_img(temp_path, target_size=(s,s))

    y = TFi.img_to_array(large)
    x = TFi.img_to_array(small)
    
    y = y.reshape(l,l,3)
    x = x.reshape(s,s,3)
    
    y_train.append(y) 
    x_train.append(x) 

filelist = sorted(os.listdir(path))
for name in filelist:
    try:
        target = PLi.open(path+name)  
        width, height = target.size 
        print(name+' '+str(width)+'x'+str(height))
        h = height//l
        w = width//l
        for j in range(0, h+1):
            for i in range(0, w+1):
                crds = (l*i, l*j, l*(i+1), l*(j+1))
                cut(path+name, crds)
            
    except BaseException:
        print ('Err '+name)

x_train = np.array(x_train)
y_train = np.array(y_train)
x_train = x_train/255
y_train = y_train/255
print(x_train.shape)
print(y_train.shape)

with open('./x_train.pickle', 'wb') as f:
    pickle.dump(x_train, f)
with open('./y_train.pickle', 'wb') as f:
    pickle.dump(y_train, f)

Следует учесть, что этот алгоритм «насилует» жёсткий диск, так как постоянно производит перезапись. В моём случае это не принципиально — имеется копеечный SSD, именно для таких случаев. Есть и ещё нюанс — нельзя просто взять и сохранить файл более 4Gb в FAT32. Исходных картинок не должно быть слишком много.

Алгоритм программы обучения нейронной сети:

Загружает дата сет из указанной директории
Создаёт нейронную свёрточную сеть
Используя дата сет, обучает сеть
Сохраняет лучшие веса для нейронной сети
Вход: 2 файла x_train, y_train
Выход: файл с весами обученной нейронной сети.

Python код

import pickle
from tensorflow.keras.optimizers import Adam
from tensorflow.python.keras.layers import Dense
from tensorflow.python.keras.layers import Conv2D
from tensorflow.python.keras.layers import UpSampling2D
from tensorflow.python.keras.models import Sequential
from tensorflow.keras.callbacks import ModelCheckpoint as ChPt



with open('./x_train.pickle', 'rb') as f:
    x_train = pickle.load( f)
with open('./y_train.pickle', 'rb') as f:
    y_train = pickle.load( f)
    
model = Sequential([
    Dense(3, input_shape=(32,32,3) ,activation='linear'),
    UpSampling2D(size=(2), data_format=None),
    Conv2D(3, (3, 3), activation='relu', padding='same'),
])

model.compile(loss='mse', optimizer=Adam(learning_rate=0.00002),metrics=['accuracy'])

print(model.summary())

best_w=ChPt('./fcn_best.h5',
            monitor='val_accuracy',
            verbose=1,
            save_best_only=True,
            save_weights_only=True,
            mode='auto',
            save_freq='epoch')
last_w=ChPt('./fcn_last.h5',
            monitor='val_accuracy',
            verbose=1,
            save_best_only=False,
            save_weights_only=True,
            mode='auto',
            save_freq='epoch')
callbacks=[best_w, last_w]

model.fit(x_train, y_train ,
          steps_per_epoch=80,
          callbacks=callbacks,
          validation_split=0.25,
          batch_size=9, epochs=99,
          verbose=1, shuffle=True, 
          use_multiprocessing=True )

Архитектура сети приведена элементарная, но даже она работает, хотя результат не далеко ушёл от интерполяции.

Задача:

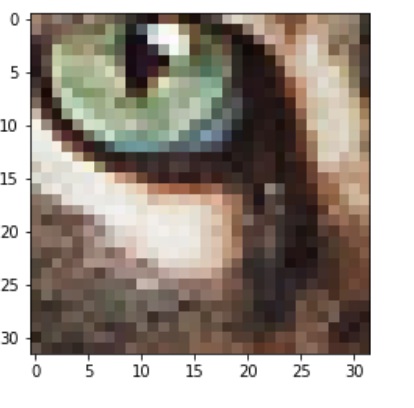
Правильный ответ:

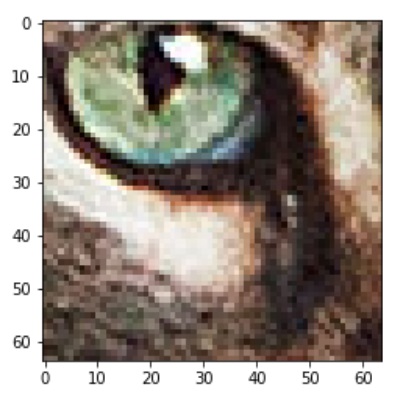
Предсказание нейронной сети:

В нейронных сетях самое интересное — придумать внутреннюю структуру, чем и предлагаю заняться читателю.

Дальше всё просто — разрезаем картинку, прогоняем кусочки через сетку с загруженными весами. Что бы результат работы нейронки можно было разглядывать не по одному квадрату, а целиком, картинку следует склеить обратно.

У получаемых в ответе квадратов 64х64 точек, периметром являются 252 из 4096 — более 6% точек. Это — область с низкой вероятностью предсказания, так как их соседи утрачены на этапе разрезания. А значит, на полученной картинке будут полосы в местах стыков квадратов.

Эти места мы прикроем предсказаниями этой же картинки, но разрезанной со сдвигом на пол квадрата.

Алгоритм сборщика:

Создаёт нейронную сеть
Из указанных директорий загружает веса нейронной сети и целевое изображение, делит его на квадраты, использует эти квадраты для предсказания при помощи нейронной сети. Из полученных квадратов собирает улучшенное изображение.
Сохраняет полученное изображение на диск.
Вход: файл с весами нейронной сети, картинка.
Выход: — картинка с удвоенным разрешением.

Python-код

import os
import pickle
import numpy as np
from PIL import Image as PLi
from tensorflow.keras.preprocessing import image as TFi
from tensorflow.keras.optimizers import Adam
from tensorflow.python.keras.layers import Dense
from tensorflow.python.keras.layers import Conv2D
from tensorflow.python.keras.layers import UpSampling2D
from tensorflow.python.keras.models import Sequential
from tensorflow.keras.callbacks import ModelCheckpoint as ChPt

with open('./x_train.pickle', 'rb') as f:
    x_train = pickle.load( f)
with open('./y_train.pickle', 'rb') as f:
    y_train = pickle.load( f)
    
model = Sequential([
    Dense(3, input_shape=(32,32,3) ,activation='linear'),
    UpSampling2D(size=(2), data_format=None),
    Conv2D(3, (3, 3), activation='relu', padding='same'),
])

model.compile(loss='mse', metrics=['accuracy'])
   
model.load_weights('fcn_best.h5')
path = './target/'
temp_location = './target/temp/builded.bmp'
out_location = "./target/temp/out.bmp"
x0_build = []
x1_build = []
x2_build = []
x3_build = []
def build(image_path, coords, target):
    
    obj = PLi.open(image_path)
    builded = obj.crop(coords)
    builded.save(temp_location) 
    img = TFi.load_img(temp_location, target_size=(32, 32))
    x = np.array(TFi.img_to_array(img))
    x = x.reshape(32,32,3)
    target.append(x) 
   
filelist = sorted(os.listdir(path))
for img in filelist:
    try:
        if img.endswith('.bmp') or img.endswith('.jpg'):
            image = PLi.open(path+img) 
            width, height = image.size
            print(img + ' ' + str(width) + 'x' + str(height))
            a = height//32
            b = width//32
            for j in range(1,a+2):
                for i in range(1,b+2):
                    build(path+img, (32*(i-1),32*(j-1),32*i,32*j), x0_build) 
                    build(path+img, ((32*i-16),32*(j-1),(32*i+16),32*j), x1_build)
                    build(path+img, (32*(i-1),32*j-16,32*i,32*j+16), x2_build)
                    build(path+img, (32*i-16,32*j-16,32*i+16,32*j+16), x3_build)
            
    except BaseException:
        print ('Err ' + img)

x0_build = np.array(x0_build)
x0_build = x0_build.astype('float')
x1_build = np.array(x1_build)
x1_build = x1_build.astype('float')
x2_build = np.array(x2_build)
x2_build = x2_build.astype('float')
x3_build = np.array(x3_build)
x3_build = x3_build.astype('float')
predictionsB = model.predict(x0_build)
predictionsB1 = model.predict(x1_build)
predictionsB2 = model.predict(x2_build)
predictionsB3 = model.predict(x3_build)  
filelist = sorted(os.listdir(path))
n = 4
for img in filelist:
    try:
        if img.endswith('.bmp') or img.endswith('.jpg'):
            image = PLi.open(path+img) 
            width, height = image.size 
            out = PLi.new('RGB', (width*2, height*2))
            a = height//32
            b = width//32
            k = 0
            for i in range (0,a+1):
                for j in range (0,b+1):
                
                    im = predictionsB[k]
                    im = im.astype(np.uint8)
                    _image = PLi.fromarray(im ,'RGB')
                    _image_ = _image.crop((n,n,64-n,64-n))
  
                    im1 = predictionsB1[k]  
                    im1 = im1.astype(np.uint8)
                    _image1 = PLi.fromarray(im1 ,'RGB')
                    _image1_ = _image1.crop((n,n,64-n,64-n))

                    im2 = predictionsB2[k]   
                    im2 = im2.astype(np.uint8)
                    _image2 = PLi.fromarray(im2 ,'RGB')
                    _image2_ = _image2.crop((n,n,64-n,64-n))

                    im3 = predictionsB3[k]
                    im3 = im3.astype(np.uint8)
                    _image3 = PLi.fromarray(im3 ,'RGB')
                    _image3_ = _image3.crop((n,n,64-n,64-n))
                
                    out.paste(_image_, (j*64+n,i*64+n))
                    out.paste(_image1_, ((j*64+32+n),(i*64+n)))
                    out.paste(_image2_, ((j*64+n),(i*64+32+n)))
                    out.paste(_image3_, ((j*64+32+n),(i*64+32+n)))
                    k = k+1 

            out.save(out_location, quality=100)
    except BaseException:
        print ('Err ')
print('Done')

Набор предложенных программ достаточно вариативен, при минимальном вмешательстве в код. Например, если немного изменить парсер, то легко получить набор данных с шумами, и тогда можно попробовать собрать «денойзер» или «шумодав». Надеюсь, дорогой читатель, теперь и ты будешь весело проводить занятные эксперименты. А я смогу безнаказанно выложить свои рассуждения по поводу возможной архитектуры сети для озвученной выше задачи. Но это уже в следующий раз.

7.3.