https://habr.com/ru/post/526460/

• Python
• Программирование

Данная статья — пятая в серии. Ссылки на предыдущие статьи: первая, вторая, третья, четвертая

5.1 Информационная энтропия (Средний объем информации)

При создании дерева решений из данных алгоритм ID3 использует индекс, называемый информационной энтропией, чтобы определить, какой атрибут следует использовать для ветвления с наиболее эффективным распределением данных.

В начале, определимся с понятием объем информации. Интуитивно понятно, что объем данных = сложность, запутанность данных. Дерево решений собирает данные с одинаковыми значениями классов с каждого ветвления, таким образом снижая степень запутанности значений класса. Следовательно, при выборе атрибута, согласно которому лучше всего проводить ветвление, опираться стоит на то, насколько простыми стали данные после разветвления.

5.1.1 Определяем понятие объем информации

Объем данных, по сути, это ценность полученной информации.
Предположим, что информация о явлениях с низкой вероятностью возникновения (например, данные, согласно которым произойдет то или иное явление), встречается гораздо чаще, чем информация о событиях, которые произойдут с высокой вероятностью.

Например, знание правильного ответа из пяти предложенных вариантов, по объему информации больше, чем знание правильного ответа из двух вариантов.

И для того, чтобы передать это знание другому человеку, представим, что оно закодировано как двоичное число и отправлено по каналу связи. В данном случае объем такого сообщения (длина в битах) и будет определяться как объем информации.



Когда вероятность того, что событие E произойдет, равна P (E), объем информации I (E), который знает, что событие E произошло, определяется следующим образом.

I(E)=log2(1/P(E))=−log2P(E)

5.1.2 Что такое информационная энтропия (средний объем информации)

У любого атрибута есть несколько значений. Например атрибут “Погода” представлен в 3 вариантах: “Ясно”, “Облачно”, “Дождь”. Среднее значение атрибутов того объема информации, который был получен из каждой вероятности появления события и называется энтропией (средним объемом информации).

В следующей формуле она представления буквой Н.

H=−∑E∈ΩP(E)log2⁡P(E)

Например, рассчитать значение энтропии 2-ух представленных на рисунке атрибутов, можно следующим образом. Более смешанная, хаотичная левая сторона имеет высокое значение энтропии, по сравнению с черной правой стороной, имеющей низкое значение энтропии.



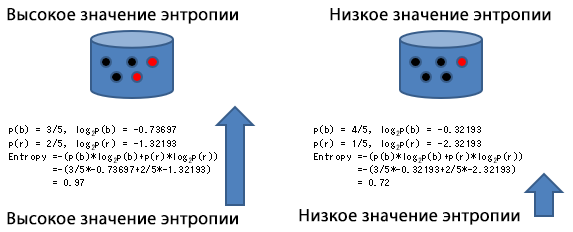
Однако, даже не используя запутанные формулы, из примера сверху можно понять, что правой стороне не хватает сложности, если посмотреть на количество черных точек. Можно, например, рассмотреть случай с добавлением желтой точки, создав тем самым ситуацию с 3 значениями. Информационную энтропию можно вычислить одинаковым образом как для двух значений, так и для трех значений, что делает ее, можно сказать, унифицированной и простой в обращении.

В примере ниже, несмотря на одинаковое количество черных точек с обеих сторон, значение энтропии будет выше на стороне, где присутствуют желтый и красный цвет, нежели чем на стороне, где оставшиеся точки только красные.



И алгоритм ID3 ищет значения атрибутов, которые разделяют данные на группы с более низкой энтропией.

5.2 Вычисление информационной энтропии

Информационная энтропия может быть вычислена с помощью следующего лямбда-выражения с DataFrame в качестве ввода и значением энтропии в качестве вывода.

entropy = lambda df:-reduce(lambda x,y:x+y,map(lambda x:(x/len(df))*math.log2(x/len(df)),df.iloc[:,-1].value_counts()))

Так как в данном лямбда-выражении уже присутствует другое лямбда-выражение, можно все немного упорядочить, и получится следующее:

entropy = lambda df:-reduce( #4.reduce создает одно значение из всех элементов массива.
    lambda x,y:x+y,#5.Складываем значения энтропии, полученные из индивидуальных значений (9,5).
    map( #2.Преобразовываем число (9,5) частотного массива (["○": 9, "×": 5]) в энтропию согласно следующему лямбда-выражению
        lambda x:(x/len(df))*math.log2(x/len(df)),#3.Вычисляем P(E)log2(P(E))
        df.iloc[:,-1].value_counts() #1.Частота последнего столбца DataFrame（например:["○":9,"×":5]）
    )
)

Данное выражение можно упорядочить следующим образом:

1. df.iloc[:,-1]извлекает последний столбец DataFrame, а value_counts дает его частотное распределение (пример частотного распределения: ["○": 9, "×": 5])
2. map преобразует каждое из значений частотного распределения (например, 9,5) в значения энтропии.
3. (x / len (df)) * math.log2 (x / len (df)) вычисляет формулу P (E) log2⁡P (E) для одного значения энтропии.
4. reduce используется для создания единого значения из всех элементов массива. Например, его можно использовать для расчета сумм, средних значений и т. д.
5. Лямбда-выражение x, y: x + y дает сумму двух аргументов (x, y), то есть сумму массивов. Это часть с “сигмой” в формуле энтропии (−∑E∈ΩP(E)log2⁡P(E)). Так как выражение имеет минус в начале, оно также имеет минус перед reduce в программе.

5.2.1 Вычисление информационной энтропии

Информационная энтропия для следующих данных составляет 0,9402859586706309.

d = {"Гольф":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"]}
# Энтропия равна 0.9402859586706309

С другой стороны, в случае, если первые два x изменяются на ○, ○ станут доминирующими данными (сложность снизится), то энтропия будет равна 0,74959525725948.

d = {"Гольф":["○","○","○","○","○","×","○","×","○","○","○","○","○","×"]}
# Энтропия равна 0.74959525725948

Ниже приведен список всех программ, вычисляющих информационную энтропию.

import pandas as pd
from functools import reduce
import math

d = {"Гольф":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"]}
df0 = pd.DataFrame(d)

entropy = lambda df:-reduce(
    lambda x,y:x+y,
    map(
        lambda x:(x/len(df))*math.log2(x/len(df)),
        df.iloc[:,-1].value_counts()
    )
)

print(entropy(df0)) # Вывод 0.9402859586706309

Спасибо за прочтение!

Мы будем очень рады, если вы расскажете нам, понравилась ли вам данная статья, понятен ли перевод, была ли она вам полезна?