https://habrahabr.ru/post/326296/Введение
В статье [1] я в строгом соответствии с общеизвестной теорией колебательных процессов рассмотрел колебательное звено, построив переходные процессы с применением библиотек SymPy и NumPy.
Первым был рассмотрен случай апериодических и свободных затухающих колебаний, инициируемых бесконечным импульсом силы постоянной амплитуды.
Вторым был рассмотрен случай отрицательного демпфирования (который я не прокомментировал). Отрицательное демпфирование можно наблюдать, когда под горизонтально подвешенного в центре на двух пружинах кубике движется лента качающееся его одной его гранью.
Лента вовлекает кубик в движение силой трения о поверхность грани. Когда упругие силы пружин, действующие в одну сторону, превышают силу трения, кубик возвращается в начальное положение и колебательный цикл повторяется. Всё что касается колебательного звена, достаточно исследовано и разуметься не претендует на научное исследование. Однако надеюсь, что любителям Python само решение было не безинтересно. Теперь с той же надеждой хочу разобрать более сложный случай поведения колебательного звена под действием возбуждающей силы изменяющейся по гармоническому закону на частоте резонанса системы.
Начну с тривиального дифференциального уравнения движения, которое описывает механическую колебательную систему с сосредоточенной массой, жёсткостью и демпфированием.
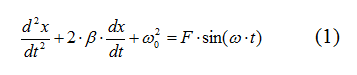
В уравнении (1) использованы следующие обозначения:
F = f / m ─ приведенная амплитуда вынуждающей колебания силы;
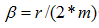
─ коэффициент затухания;
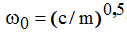
─ собственная частота колебаний системы;

─ частота вынуждающей колебания силы; m ─ сосредоточенная масса; r ─ коэффициент демпфирования; c ─ сосредоточенная жёсткость колебательной системы; x ─ координата перемещения; t ─ координата времени; f ─ амплитуда вынуждающей колебания силы.
Рассмотрим код программы для численного решения уравнения (1)import numpy as np
from sympy import *
from IPython.display import *
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
init_printing(use_latex=True)
var('t C1 C2')
u = Function("u")(t)
B=0.1#затухание
w=10#круговая частота
f=1#амплитуда силы
de = Eq(u.diff(t, t) +2*B*u.diff(t) +w**2* u, f*sin(w*t))#данные для символьного решения ДУ
display(de)# вывод данных в IDLE интерфейс
des = dsolve(de,u)#символьное решение для введенных данных
display(des)#вывод решения ДУ в IDLE интерфейс
eq1=des.rhs.subs(t,0)# начальные условия для координаты перемещения
display(eq1)#)вывод первого уравнения для С1,С2 в IDLE интерфейс
eq2=des.rhs.diff(t).subs(t,0)#начальные условия для скорости перемещения
display(eq2)#вывод второго уравнения для С1,С2 в IDLE интерфейс
seq=solve([eq1,eq2],C1,C2)#решение системы уравнений для С1,С2
display(seq)#вывод решения уравнения для С1,С2 в IDLE интерфейс
rez=des.rhs.subs([(C1,seq[C1]),(C2,seq[C2])])#постановка С1,С2 в решение ДУ
display(rez)#)вывод решения уравнения в IDLE интерфейс
g= lambdify(t, rez, "numpy")# перевод из символьного решения в числовое для NumPy
t= np.linspace(0,2*w,1000)# оцифровка в диапазоне 0-2*w с 1000 отсчётов
tt=[ i for i in t if g(i)==max(g(t))]# промежуток времени для стабилизации амплитуды АК
plt.title('Переходной процесс при затухании B -%f,'%B)# далее график
plt.xlabel('Время в секундах до стабилизации амплитуды - %iа% tt[0], fontsize=12)
plt.ylabel('Размах амплитуды при резонансе -%f'%(2*max(g(t))),fontsize=16)
plt.plot(t,g(t),color='b', linewidth=3)
plt.grid(True)
plt.show()
Предложенный код предназначен именно для исследования резонансных когда частота вынуждающей силы w равна собственной частоте w механической системы. Для наглядности графиков частота выбрана низкой w=10 c-1
Использование Python+SymPy+NumPy в отличии от известных мне публикаций в сети позволяет не только решить уравнение (1) но и установить размах амплитуды — max(g(t)), но и определить время на установление автоколебаний — tt=[ i for i in t if g(i)==max(g(t))]
Результаты решения дифференциального уравнения в приведенной программе на Python сравним с решением в ONLINE сервисе [2].
Исходное уравнение на Python. Строки кода для вывода.
de = Eq(u.diff(t, t) +2*B*u.diff(t) +w**2* u, f*sin(w*t))
display(de)
Реpультат
: Eq(100*u(t) + 0.2*Derivative(u(t), t) + Derivative(u(t), t, t), sin(10*t))
Для сервиса.
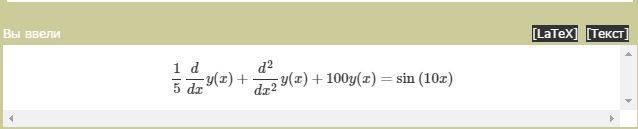
Общее решение на Python: Eq(u(t), (C1*sin(3*sqrt(1111)*t/10) + C2*cos(3*sqrt(1111)*t/10))/exp(t)**(1/10) — 0.5*cos(10*t))
Общее решение на сервисе:
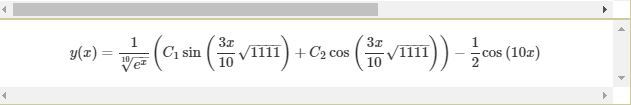
Постоянные коэффициенты C1, C2 на Python
{C2: 0.500000000000000, C1: 0.00500025001875156}
На сервисе.

Проведенное сравнение подтверждает идентичность разработанной схемы решения сервису [2] как по этапам решения, так и по результату.
Вернёмся к колебательному звену. Установим следующие значения затухания B=[0.1,0.25,0.5] оставляя неизменными остальные параметры колебательной системы получим следующие графики.
 Этапы решения дифференциального уравнения колебаний.
Этапы решения дифференциального уравнения колебаний.
Eq(100*u(t) + 0.2*Derivative(u(t), t) + Derivative(u(t), t, t), sin(10*t))
Eq(u(t), (C1*sin(3*sqrt(1111)*t/10) + C2*cos(3*sqrt(1111)*t/10))/exp(t)**(1/10) — 0.5*cos(10*t))
C2 — 0.5
3*sqrt(1111)*C1/10 — C2/10
{C2: 0.500000000000000, C1: 0.00500025001875156}
(0.00500025001875156*sin(3*sqrt(1111)*t/10) + 0.5*cos(3*sqrt(1111)*t/10))/exp(t)**(1/10) — 0.5*cos(10*t)
 Этапы решения дифференциального уравнения колебаний.
Этапы решения дифференциального уравнения колебаний.
Eq(100*u(t) + 0.5*Derivative(u(t), t) + Derivative(u(t), t, t), sin(10*t))
Eq(u(t), (C1*sin(sqrt(1599)*t/4) + C2*cos(sqrt(1599)*t/4))/exp(t)**(1/4) — 0.2*cos(10*t))
C2 — 0.2
sqrt(1599)*C1/4 — C2/4
{C2: 0.200000000000000, C1: 0.00500156323280355}
(0.00500156323280355*sin(sqrt(1599)*t/4) + 0.2*cos(sqrt(1599)*t/4))/exp(t)**(1/4) — 0.2*cos(10*t)
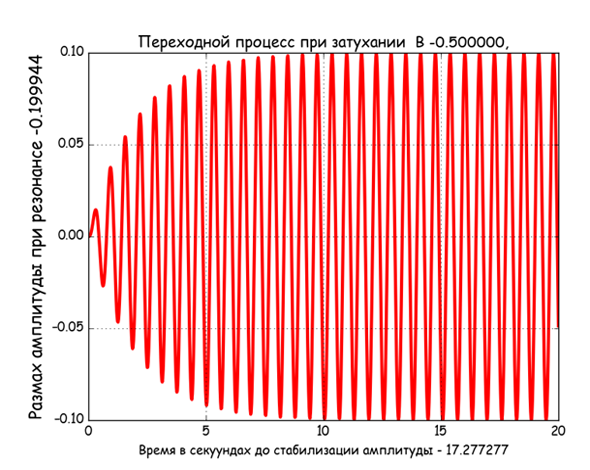 Этапы решения дифференциального уравнения колебаний.
Этапы решения дифференциального уравнения колебаний.
Eq(100*u(t) + 1.0*Derivative(u(t), t) + Derivative(u(t), t, t), sin(10*t))
Eq(u(t), (C1*sin(sqrt(399)*t/2) + C2*cos(sqrt(399)*t/2))/sqrt(exp(t)) — 0.1*cos(10*t))
C2 — 0.1
sqrt(399)*C1/2 — C2/2
{C1: 0.00500626174321759, C2: 0.100000000000000}
(0.00500626174321759*sin(sqrt(399)*t/2) + 0.1*cos(sqrt(399)*t/2))/sqrt(exp(t)) — 0.1*cos(10*t)
Из приведенных графиков следует, что время установления резонансных колебаний при малых затуханиях изменяются не значительно (19,8 -19,16. С ростом затухания изменение времени становиться заметным(19,16-- 17,28). Тогда как размах амплитуды уменьшается пропорционально росту затухания. Время восстановления стационарной амплитуды резонансных колебаний важный параметр при использовании таких колебаний, например при измерении присоединённой массы.
Вывод
Предложенная модель может быть использована как при изучении резонансных процессов, так и в учебных целях.
Ссылки
- Модель колебательного звена с применением символьного и численного решений дифференциального уравнения на SymPy и NumPy.
- Pешение дифференциальных уравнений онлайн.

