https://habrahabr.ru/post/324158/

• Python

Зачем это нужно

Метод гармонической линеаризации широко используется для анализа нелинейных систем [1]. Этот метод используется для определения условий возникновения автоколебаний в системах второго и более высокого порядка. При гармонической линеаризации должны выполняться два следующих условия. Замкнутая линейная система должна состоять из двух частей ─ линейной и нелинейной. Линейная часть должна обладать хорошими фильтрующими свойствами для высших гармоник[2]. Системы автоматического управления и регулирования содержат исполнительные механизмы, содержащие нелинейные элементы, поэтому их анализ является весьма актуальной проблемой.

Основной алгоритм

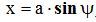
Пусть на вход нелинейного элемента поступает гармонический сигнал , где Преобразовав выходной сигнал в ряд Фурье только для первой гармоники. Получим:
С учётом (1),(2) общее уравнение нелинейного элемента можно представить в виде[3]:
где ─ действительная «а» – мнимая составляющая коэффициента гармонической линеаризации полученных из условия последующей фильтрации высших гармоник; ─ круговая частота; — оператор дифференцирования.

Постановка задачи

Будем сравнивать два нелинейных элемента приведённых на рис.1,2, с целью выяснить стабильность амплитуды.

Рис.1 Нелинейность типа «насыщение»

Используя (1), пока только для действительной части, получим:


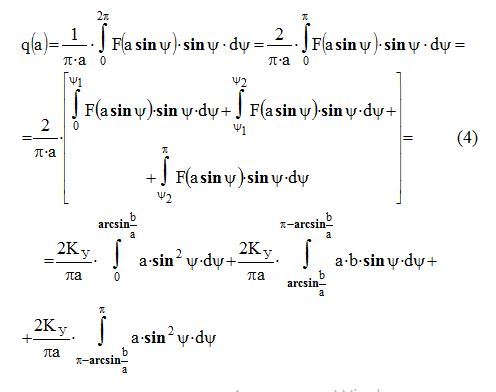
Рис.2 Нелинейность типа «обрыв»

Аналогично используя (1), пока только для действительной части, получим:

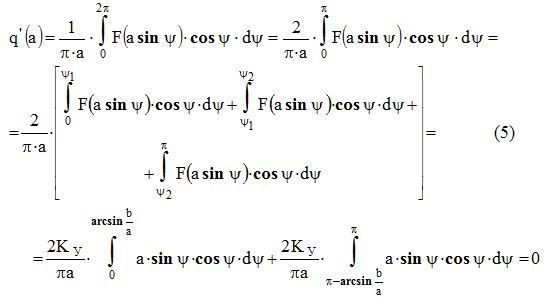
Реализация (4),(5) на Python

#!/usr/bin/python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt # модуль для построения графика
import matplotlib as mpl #модуль для установки шрифта
mpl.rcParams['font.family'] = 'fantasy'# шрифт
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Aria'# шрифт
import scipy.integrate as spint # модуля для числового интегрирования
import math # модуль для элементарных функций
import numpy as np# модуль для работы с массивами
q=[]# список для коэффициента -насыщение
p=[]#список для коэффициента -обрыв
c=[]# список для границы линейной области
k=1#переменная для установки линейной области
for  m in np.arange(1.0,4,0.1):  # задание диапазона относительной амплитуды  
    def f(x): # вычисление интегралов для коэффициентов ряда Фурье
        return k*(math.sin(x))**2
    a = 0# нижний предел интегрирования
    b =math.asin(1/m)# верхний предел интегрирования
    z=spint.quad(f,a,b)[0]# результат интегрирования
    a =math.pi-math.asin(1/m)#нижний предел интегрирования
    b =math.pi#верхний предел интегрирования
    z1=spint.quad(f,a,b)[0]#результат интегрирования
    q.append(round(z+z1,3))# числовые значения коэффициента - обрыв
    def f1(x):# вычисление интегралов для коэффициентов ряда Фурье
        return (k/m)*(math.sin(x))
    a =math.asin(1/m)#нижний предел интегрирования
    b =math.pi-math.asin(1/m)#верхний предел интегрирования
    z2=spint.quad(f1,a,b)[0] #результат интегрирования
    p.append(round(z+z1+z2,3))#числовые значения коэффициента - насыщение
x=np.arange(1.0,4,0.1)# числовые значения для координаты х для коэффициентов
x2=np.arange(0.0,1.1,0.1)#числовые значения для координаты х для линейной области
for  i in np.arange(0.0,1.1,0.1):# диапазон значений для линейной  области
    c.append(p[0])
plt.title('Коэффициенты гармонической линеаризации', size=14)# заголовок графика
plt.xlabel('Относительная амплитуда сигнала', size=14)# подпись под осью х
plt.ylabel('Приведенный коэффициен усиления', size=14)# подпись под осью у
plt.plot(x, q, color='r', linewidth=2, label='Нелинейность-- обрыв')# построение графика и легенда
plt.plot(x, p, color='b',linewidth=2, label='Нелинейность насыщение')#построение графика и легенда
plt.plot(x2, c, color='g', linewidth=2, label='Линейная область')#построение графика и легенда
plt.legend(loc='best')# лучшее расположение легенды
plt.grid(True)# сетка
plt.show()# визуализация

Результат (да в jpeg, но это график!)
Кстати интегрирование при помощи import scipy.integrate as spint осуществляться стабильно и без ошибок.



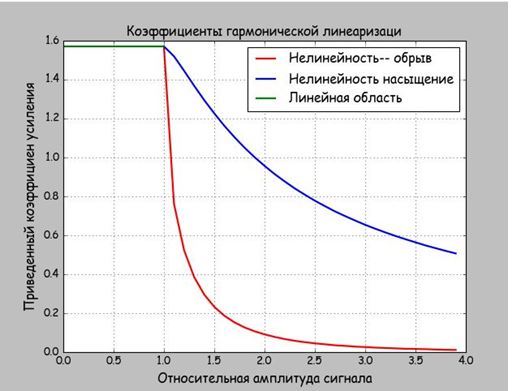
Из графика с полной очевидностью следует, что нелинейный элемент, приведенный на рис.2, при условии фильтрации высших гармоник обеспечит большую стабильность амплитуды, чем приведённый на рис.1. Более детальный анализ покажет и меньший процент гармоник, но это тема другой статьи.

Вы, конечно, спросите «А как же другие нелинейности, может они ещё лучше?». Я делал это для низкочастотного (до 5кгц) усилителя специального назначения с типовыми характеристиками, приведенными на рис.1,2. Кстати, характеристики рис.2 нет ни в одном справочнике.

Вариант сокращения кода программы

Можно использовать символьные вычисления, например, так:

from sympy import *
import matplotlib.pyplot as plt
import numpy as np
x=Symbol('x')
m=Symbol('m')
z=integrate(sin(x)**2, (x,0,asinh(m)))+integrate(sin(x)**2, (x,pi-asinh(m),pi)) #символьное преобразование для коэффициент - обрыв
z1=integrate(sin(x)**2, (x,0,asinh(m)))+integrate(m*sin(x), (x,asinh(m),pi-asinh(m)) )+integrate(sin(x)**2, (x,pi-asinh(m),pi))#  то же для насыщения 
print(z)
print(z1)

Получим:-sin(asinh(m))*cos(asinh(m)) + asinh(m)2*m*cos(asinh(m)) — sin(asinh(m))*cos(asinh(m)) + asinh(m)

Программное упрощение (simplify(z)) ничего не даёт, поэтому используем соотношения: , получим:

Вводим отношение амплитуды к порогу ограничения и окончательно получим:

Соотношение (6) решение уравнения (5), система (7) решение уравнения (4).

Выводы

В статье рассмотрена методика сравнительного анализа нелинейных элементов методом гармонической линеаризации.

Ссылки

1. Воронов А.А. Основы теории автоматического управления. Особыелинейные и нелинейные системы. – М.: Энергоиздат, 1981, 300 с.
2. Гольдфарб Л.С., Балтрушевич А.В., Нетушил А.В. Теорияавтоматического управления. – М.: Высшая школа, 1976, 430 с
3. Хлыпало Е.Н. Нелинейные системы автоматического регулирования / Е.Н. Хлыпало. – Л.: Энергия, 1967. – 343 с.