https://habrahabr.ru/post/345714/- Разработка под Windows
- Математика
- Анализ и проектирование систем
- Алгоритмы
- Python
 Введение
Введение
Важнейшей задачей автоматического управления любыми технологическими процессами является разработка математического описания, расчет и анализ динамики автоматических систем регулирования (АСР).
Практика промышленного использования микропроцессорных регулирующих приборов (МРП) показала, что “идеальные алгоритмы” физически не реализуемы. Синтезированная на их основе АСР не отражает поведение реальной системы [1].
Отклонения алгоритмов от идеализированных при определенных условиях, например, для релейно-импульсных регуляторов, когда скорость исполнительного механизма соответствует реальной динамике объекта, поведение реальной системы с достаточной степенью точности соответствует результатам математической модели.
Релейно-импульсные регуляторы применяются в микропроцессорных регулирующих приборах, где наблюдается следующая тенденция. Например, в публикации [2] описаны возможности применения протокола modbus для создания собственной Scada системы на базе Python.
В публикации [3] описано использование Python для работы с Arduino. Продолжаю эту тенденцию и я в надежде, что Python окончательно овладеет этой новой областью применения.
1.Типовые линейные алгоритмы регулирования
Привожу идеальные алгоритмы регулирования, которые определяются уравнениями:
П- алгоритм:
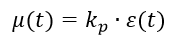
ПИ- алгоритм:
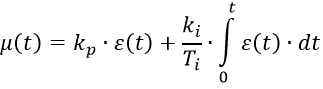
ПИД- алгоритм:

где
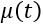
– регулирующее воздействие;
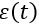
– сигнал рассогласования; Kp,Ki,Kd — коэффициент передачи и Ti,Td постоянные времени соответствующих звеньев (параметры настройки регуляторов).
Все переходные характеристики регуляторов с учётом параметров настройки можно представить одной общей формулой, избегая неопределённости от деления на 0:
from numpy import e,arange
def hp(t,Kp,Ki,Kd,Td):
if t<0:
z=0
elif Td==0:
z=Kp+Ki*t
else:
z=Kp+Ki*t+Kp*Kd*e**(-t/Td)
return z
Следует заметить, что ПИД-регулятор в идеальном виде физически не реализуем, поэтому представлен в виде:
Kp+Ki*t+Kp*Kd*e**(-t/Td) для имитации идеальности.
Переходные характеристики идеальных регуляторов#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
from numpy import e,arange
def hp(t,Kp,Ki,Kd,Td):
if t<0:
z=0
elif Td==0:
z=Kp+Ki*t
else:
z=Kp+Ki*t+Kp*Kd*e**(-t/Td)
return z
x=arange(-2,10,0.01)
y=[hp(t,2,0,0,0) for t in x]
y1=[hp(t,2,0.25,0,0) for t in x]
y2=[hp(t,2,0.25,2,2) for t in x]
plt.title('Переходные характеристики регуляторов')
plt.plot(x, y, linewidth=2, label='П регулятор')
plt.plot(x, y1, linewidth=2, label='ПИ регулятор')
plt.plot(x, y2, linewidth=2, label='ПИД регулятор ')
plt.legend(loc='best')
plt.grid(True)
plt.show()
Характер переходных процессов показан на графике:
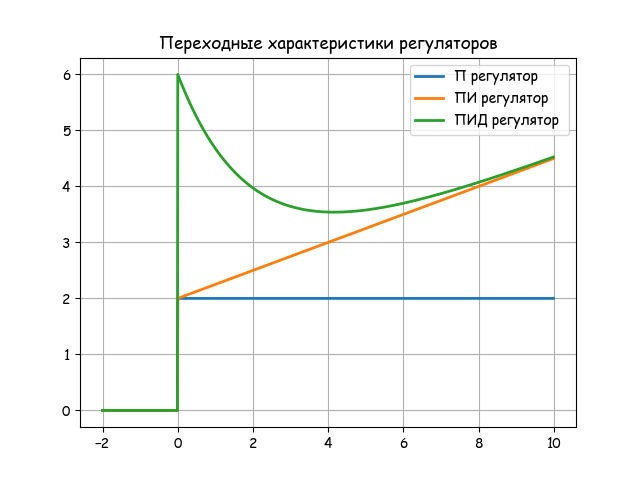
На основе типовых идеальных алгоритмов регулирования в теории управления развиты методы оптимального параметрического синтеза и исследованы общие свойства АСР.
В промышленных автоматических регуляторах типовые алгоритмы реализуется приближенно. Отклонение алгоритма регулирования от идеального не оказывает существенного влияния на поведение системы, если регулятор работает в области “нормальных” режимов.
Для этого необходимо знать и учитывать существенные особенности реального алгоритма, обусловленные способом его технической реализации. В практике автоматизации получили широкое распространение электрические (электронные) регуляторы косвенного действия в форме виртуальных модулей микропроцессорных контроллеров.
Рассмотрим классификацию автоматических электрических регуляторов по способу реализации алгоритма [1]:
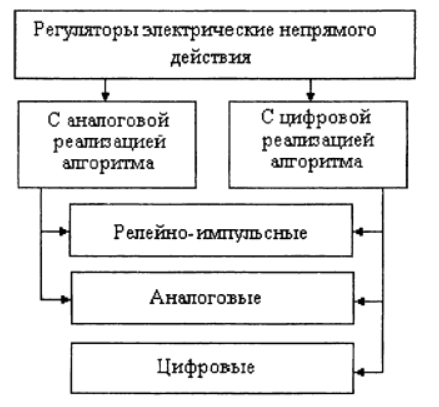
В соответствии с представленной классификацией в этой и следующих публикациях будет рассматриваться реализация математических моделей регуляторов средствами Python.
2. Регуляторы релейно-импульсного действия
В автоматических системах управления технологическими процессами используются исполнительные механизмы (ЭИМ) с электрическими асинхронными реверсивными двигателями с постоянной частотой вращения выходного вала. Это и определило способ реализации алгоритма регулирования.
Принцип реализации ПИ-алгоритма при наличии ЭИМ постоянной скорости иллюстрирует схема, представленная на рисунке:
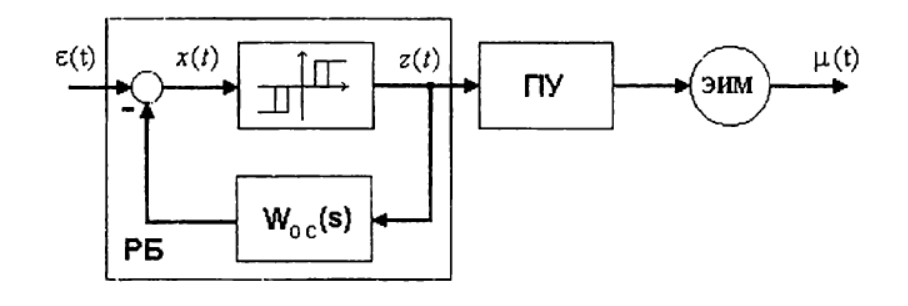
Регулирующий блок (РБ) формирует управляющие ЭИМ прямоугольные импульсы постоянной амплитуды, длительность и скважность которых зависят от значений параметров настройки регулятора и значения входного сигнала.
Прямой канал РБ содержит нелинейный элемент – трехпозиционное реле с зоной нечувствительности ∆н зоной возврата ∆в, приведённое на рисунке:
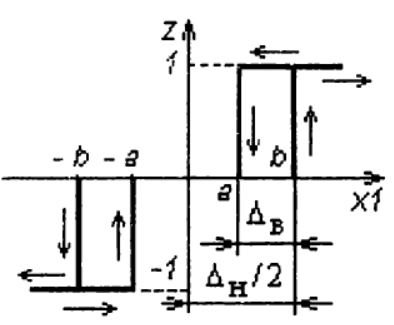
Модель нелинейного элемента#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
from numpy import arange,sin,cos,sign
def z(t,a,b):
if -a<4*sin(t)<b and 4*cos(t)>0:
z=0
elif -b<4*sin(t)<a and 4*cos(t)<0:
z=0
else:
z=sign(sin(t))
return z
x=arange(0,6,0.005)
y=[4*sin(t) for t in x]
y1=[z(t,2,3) for t in x]
y2=[2 for t in x]
y3=[3 for t in x]
plt.figure()
plt.title('Дискретная модель РЭ: вход -выход')
plt.plot(x, y, linewidth=2, label='Входной сигнал')
plt.plot(x, y1, linewidth=2, label='Выходной сигнал')
plt.plot(x, y2, linewidth=1, label='2 ')
plt.plot(x, y3,linewidth=1, label='3')
plt.legend(loc='best')
plt.grid(True)
plt.figure()
plt.title('Дискретная модель РЭ. Характеристика РЭ')
plt.plot(y, y1, linewidth=2, label=' Характеристика РЭ')
plt.legend(loc='best')
plt.grid(True)
plt.show()
Анализируем результат работы модели по двум следующим графикам:
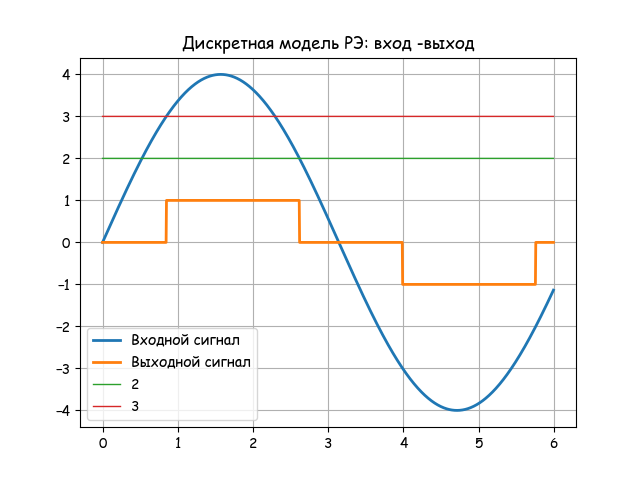
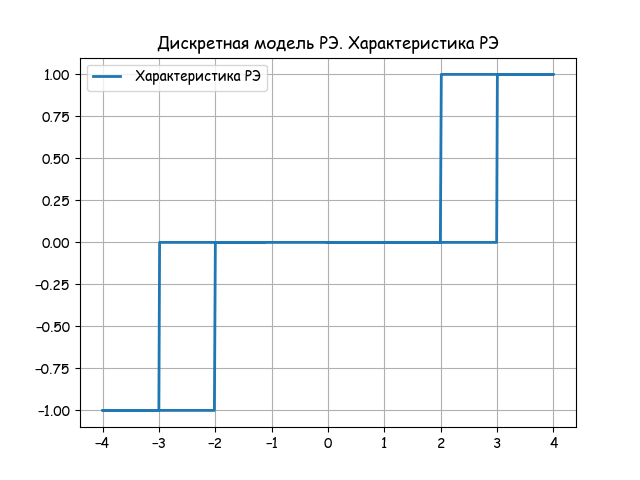
Дискретная модель РЭ основана на разностных уравнениях. Формирующая ПИ-алгоритм обратная связь реализована с использованием апериодического звена с передаточной функцией:
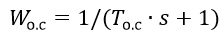
Регулирующий блок (РБ) представляет собой широтно-импульсный модулятор (ШИМ), который может быть построен с использованием как аналоговых, так и цифровых средств.
Регулирующий блок совместно с исполнительным механизмом постоянной скорости обеспечивают при определенных условиях достаточно точную реализацию ПИ-алгоритма:
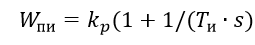
(1)
И соответственно переходной характеристики:
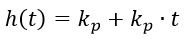
(2)
Для реализации ПИД-алгоритма ко входу ПИ-регулятора релейно-импульсного действия подключается дифференциатор W(s) по схеме:
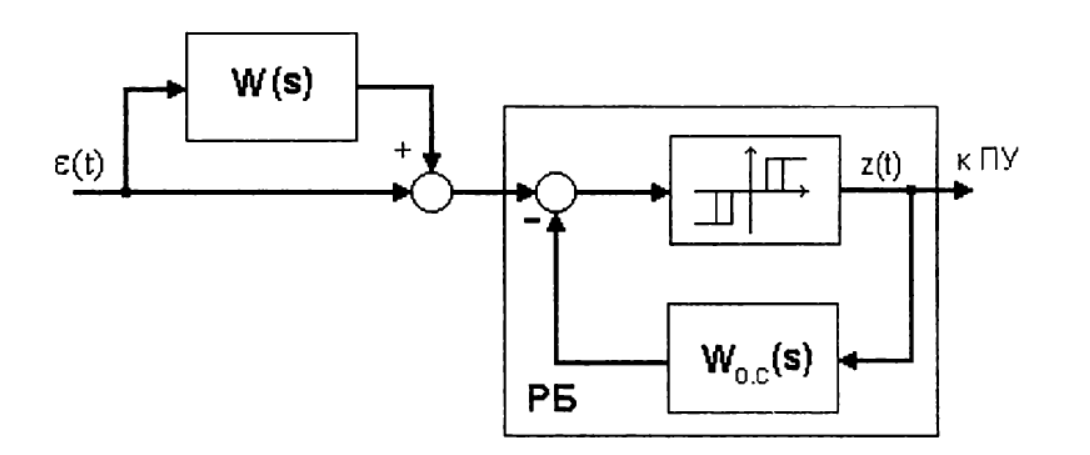
Введенная передаточная W(s) образуется одним или двумя последовательно включенными дифференцирующими звеньями. Регулирующий блок совместно с исполнительным механизмом постоянной скорости обеспечивает при определенных условиях достаточно точную реализацию ПИД-алгоритма:
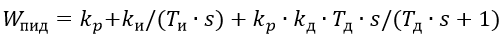
(3)
И соответственно переходной характеристики:
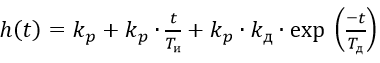
(4)
Листинг для сравнения ПИ- и ПИД-алгоритмов#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
from numpy import e,arange
def hp(t,Kp,Ti,Kd,Td):
z=Kp+Kp*t/Ti+Kp*Kd*e**(-t/Td)
return z
x=arange(0,10,0.02)
y1=[hp(t,2,2,0,0.5) for t in x]
y2=[hp(t,2,2,4,0.5) for t in x]
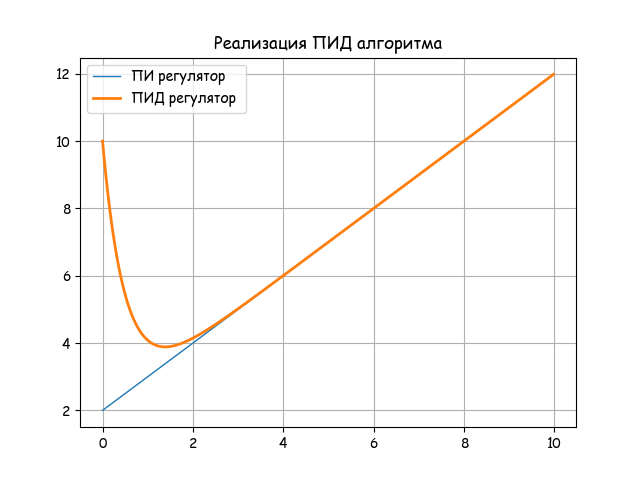
plt.title('Реализация ПИД алгоритма')
plt.plot(x, y1, linewidth=1, label='ПИ регулятор')
plt.plot(x, y2, linewidth=2, label='ПИД регулятор ')
plt.legend(loc='best')
plt.grid(True)
plt.show()
Анализируем график переходных процессов для выбранных настроек ПИ- и ПИД-алгоритмов.
Линейные модели релейно-импульсных регуляторов не исключают возможности мгновенного изменения регулирующего воздействия (выходной величины регулятора).
У реальных релейно-импульсных регуляторов перемещение выходного вала или штока ЭИМ происходит за некоторое конечное время, зависящее как от установленных значений параметров настройки, так и
скорости исполнительного механизма so.
Так, при ступенчатом изменении входного сигнала, длительность импульса на выходе регулирующего блока РБ для П-алгоритма определяется соотношением:
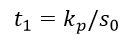
Длительность первого импульса на выходе РБ для ПИ-алгоритма определяется уравнением:
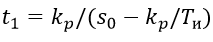
Последующие импульсы постоянной длительности tи повторяются через следующие интервалы времени:
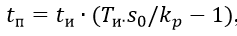
где
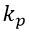
— коэффициент передачи регулятора;
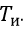
— постоянная интегрирования, с;
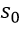
— скорость исполнительного механизма,
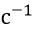
.
3. Моделирование динамики релейно-импульсных П-ПИ- и ПИД-регуляторов в неравновесных режимах
Граф релейно-импульсного ПИД-регулятора приведен на следующем рисунке:
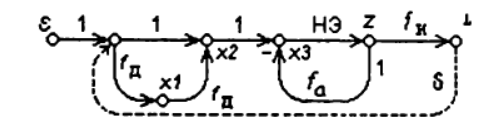
Листинг модели динамики релейно-импульсных регуляторов#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
from numpy import arange,sign
def fd(Kd,Td,dt,x,x1,y):# РД -звено (дифференциатор)
return (1-dt/Td)*y+Kd*(x-x1)
def fa(Ta,Ka,dt,x,y):# апериодическое звено (обратная связь)
return (1-dt/Ta)*y+Ka*x*dt/Ta
def fi(so,dt,x,y):# интегратор (исполнительный механизм)
return y+so*x*dt
""" Подготовка исходных данных"""
te=15;N=300;dt=0.05
x0=[0 for w in arange(0,N+1)];x1=[0 for w in arange(0,N+1)]
x2=[0 for w in arange(0,N+1)];x3=[0 for w in arange(0,N+1)]
z=[0 for w in arange(0,N+1)];z1=[0 for w in arange(0,N+1)]
z2=[0 for w in arange(0,N+1)];m=[0 for w in arange(0,N+1)]
x=[0 for w in arange(0,N+1)]
""" Численное решение"""
def P(so,Ka,Ta,a,b,Kd,Td,Dl,e):
for j in arange(0,N,1):
x0[j+1]=e-Dl*m[j]
x[j+1]=x0[j+1]+x2[j]-x3[j]
if -a<x[j+1]<b and x[j+1]>x[j]:
z1[j+1]=0
else:
z1[j+1]=sign(x[j-1])
if -b<x[j+1]<a and x[j+1]<x[j]:
z2[j+1]=0
else:
z2[j+1]=sign(x[j-1])
if x[j+1]>x[j]:
z[j+1]=z1[j+1]
else:
z[j+1]=z2[j+1]
x1[j+1]=fd(Kd,Td,dt,x0[j+1],x0[j],x1[j])
x2[j+1]=fd(1,Ta,dt,x1[j+1],x1[j],x2[j])
x3[j+1]=fa(Ta,Ka,dt,z[j+1],x3[j])
m[j+1]=fi(so,dt,z[j],m[j])
return m
NN=[j*dt for j in arange(0,N+1,1)]
#P(so,Ka,Ta,a,b,Kd,Td,Dl,e)
#PID=P(1,10,5,0.4,0.5,10,1,0,1)
#PP=P(1,0.1,0.1,0.2,0.6,0,0.2,4,1)
#PI=P(1,10,5,0.4,0.5,0,0.2,0,1)
#PI1=P(0.5,10,5,0.4,0.5,0,0.2,0,1)
plt.figure()
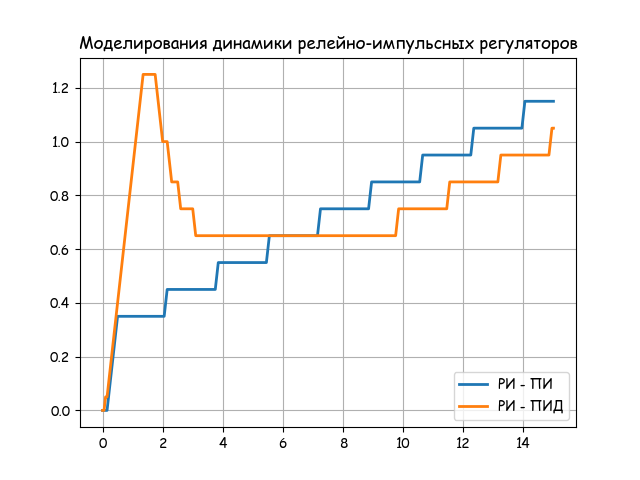
plt.title('Моделирование динамики релейно-импульсных регуляторов')
plt.plot(NN, P(1,10,5,0.4,0.5,0,0.2,0,1), linewidth=2, label='РИ - ПИ')
plt.plot(NN,P(1,10,5,0.4,0.5,10,1,0,1), linewidth=2, label='РИ - ПИД')
plt.legend(loc='best')
plt.grid(True)
plt.figure()
plt.title('Моделирование динамики релейно-импульсных регуляторов')
plt.plot(NN, P(1,10,5,0.4,0.5,0,0.2,0,1), linewidth=2, label='РИ -ПИ. Скорость ЭИМ -1 с-1')
plt.plot(NN,P(0.5,10,5,0.4,0.5,0,0.2,0,1), linewidth=2, label='РИ -ПИ.Скорость ЭИМ -0.5 с-1')
plt.plot(NN,P(1,0.1,0.1,0.2,0.6,0,0.2,4,1), linewidth=2, label='РИ -П.Скорость ЭИМ -1 с-1')
plt.legend(loc='best')
plt.grid(True)
plt.show()
Анализируем полученные результаты.
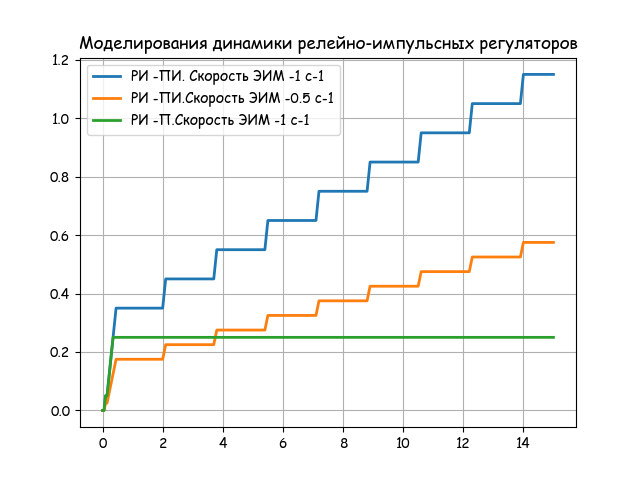
Характеристика регулятора зависит как от скорости исполнительного механизма so, так и параметров релейного элемента а, b. Значение so предопределяется типом ЭИМ и характеризуется параметром Тим — минимальное время полного хода. Для стандартных ЭИМ значения Тим равно 10,25,63, 100 и 160 с.
Значение b (половина зоны нечувствительности) устанавливается по величине допустимого отклонения, на которое регулятор не должен реагировать.
Параметры настройки регулятора Кр, Ти, Кд, Тд находятся в нелинейной зависимости от скорости исполнительного механизма so, параметров обратной связи Ка, Та и релейного элемента а, b.
Выводы
Средствами языка программирования Python, с применением метода конечных разностей, получены математические модели электронных релейно-импульсных регуляторов косвенного действия.
Полученные модели могут быть использованы при проектировании микропроцессорных регулирующих приборов.
Ссылки- Расчёт и моделирование автоматических систем регулирования в среде Mathcad.
- ScadaPy — использование OPC UA.
- Веб-сервер — ваша первая сетевая программа Arduino.

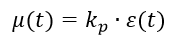
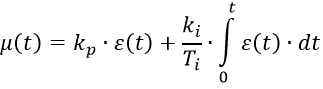

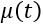 – регулирующее воздействие;
– регулирующее воздействие; 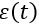 – сигнал рассогласования; Kp,Ki,Kd — коэффициент передачи и Ti,Td постоянные времени соответствующих звеньев (параметры настройки регуляторов).
– сигнал рассогласования; Kp,Ki,Kd — коэффициент передачи и Ti,Td постоянные времени соответствующих звеньев (параметры настройки регуляторов).





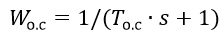
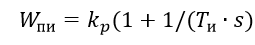 (1)
(1)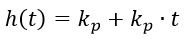 (2)
(2)
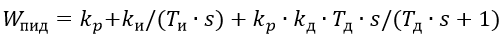 (3)
(3)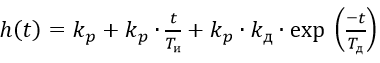 (4)
(4)
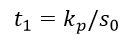
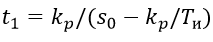
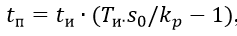
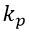 — коэффициент передачи регулятора;
— коэффициент передачи регулятора; 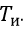 — постоянная интегрирования, с;
— постоянная интегрирования, с; 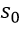 — скорость исполнительного механизма,
— скорость исполнительного механизма, 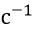 .
.

