Математическая модель динамики финансового рынка
- вторник, 31 октября 2017 г. в 03:11:47
import matplotlib.pyplot as plt
from sympy import *
from numpy import (zeros,arange,ones,matrix,linalg,linspace)
X=[797.17, 797.25, 797.15, 797.23, 797.15, 797.08, 797.05, 797.04, 797.14, 797.14, 797.1, 797.1, 797.11, 797.11, 797.11, 797.11, 797.11, 797.1, 797.1, 797.1, 797.12, 797.12, 797.12, 797.12, 797.12, 797.12, 797.1, 797.08]
n=len(X)
m=int(n/4)
Xsr=sum([w for w in X])/n
Dx=sum([(X[i]-Xsr)**2 for i in arange(0,n,1)])/(n-1)
Rxm=sum([(X[i]-Xsr)*(X[i+m]-Xsr) for i in arange(0,n-m,1)])/((n-m)*Dx)
def fRxm(m):
return sum([(X[i]-Xsr)*(X[i+m]-Xsr) for i in arange(0,n-m,1)])/((n-m)*Dx)
ym=[fRxm(m) for m in arange(0,m+1)]
xm=list(arange(0,m+1,1))
M=zeros([1,m+1])
for i in arange(0,m+1,1):
M[0,i]=fRxm(i)
plt.figure()
plt.title('График автокорреляционной функция Rx (τ). ')
plt.ylabel('Rx (τ) ')
plt.xlabel(' Номер интервала времени -m ')
plt.plot(xm, ym, 'r')
plt.grid(True)
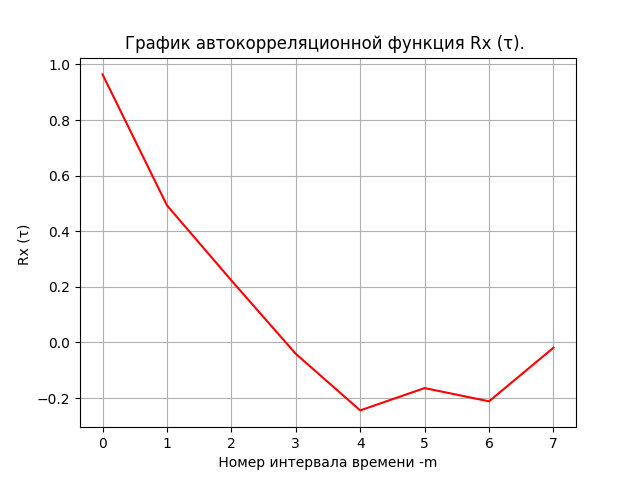
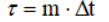 — промежуток времени (смещение) между значениями случайного процесса x(t) соответствующее значению R(m) автокорреляционной функции.
— промежуток времени (смещение) между значениями случайного процесса x(t) соответствующее значению R(m) автокорреляционной функции. влияют друг на друга, но это влияние можно предсказать со значительной ошибкой.
влияют друг на друга, но это влияние можно предсказать со значительной ошибкой.Y=[577.59, 622.61, 602.23, 554.64, 567.67, 635.47, 608.27, 620.82, 561.73, 639.0, 550.1, 609.31, 640.45, 611.92, 579.33, 552.04, 597.73, 553.4, 605.72, 647.94, 602.26, 610.99, 575.95, 638.99, 631.86, 589.89, 608.17, 619.26]
n=len(Y)
m=int(n/4)
Ysr=sum([w for w in Y])/n
Dy=sum([(Y[i]-Ysr)**2 for i in arange(0,n,1)])/(n-1)
Rxy=sum([(X[i]-Xsr)*(Y[i+m]-Ysr) for i in arange(0,n-m,1)])/((n-m)*Dx**0.5*Dy**0.5)
def fRxy(m):
return sum([(X[i]-Xsr)*(Y[i+m]-Ysr) for i in arange(0,n-m,1)])/((n-m)*Dx**0.5*Dy**0.5)
xy=[fRxy(m) for m in arange(0,m+1)]
plt.figure()
plt.title('График автокорреляционной функции Rxy (τ). ')
plt.ylabel('Rxy (τ) ')
plt.xlabel(' Номер интервала времени -m ')
plt.plot(xm, xy, 'r')
plt.grid(True)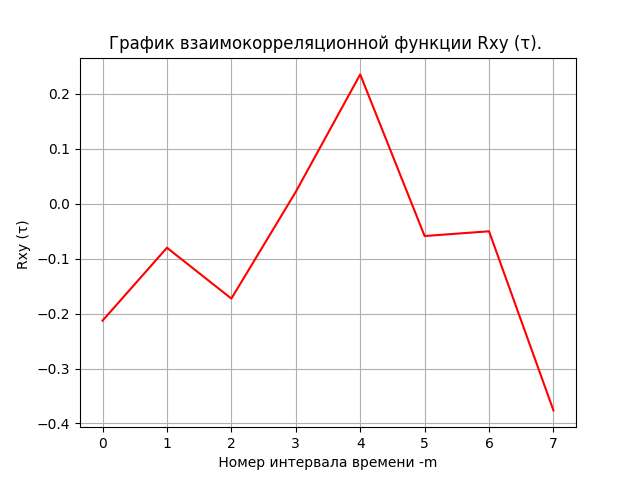
P=zeros([m,1])
for i in arange(0,m,1):
P[i,0]=fRxy(i)
Q=zeros([7,7])
for i in arange(0,7,1):
Q[0,i]=M[0,i+1]
Q[1,i]=M[0,i]
for i in arange(0,6,1):
Q[2,i+1]=M[0,i]
Q[2,0]=M[0,1]
for i in arange(0,5,1):
Q[3,i+2]=M[0,i]
Q[3,1]=M[0,1]
Q[3,0]=M[0,2]
for i in arange(0,4,1):
Q[4,i+3]=M[0,i]
Q[4,0]=M[0,3]
Q[4,1]=M[0,2]
Q[4,2]=M[0,1]
for i in arange(0,3,1):
Q[5,i+4]=M[0,i]
Q[5,0]=M[0,4]
Q[5,1]=M[0,3]
Q[5,2]=M[0,2]
Q[5,3]=M[0,1]
for i in arange(0,2,1):
Q[6,i+5]=M[0,i]
Q[6,0]=M[0,5]
Q[6,1]=M[0,4]
Q[6,2]=M[0,3]
Q[6,3]=M[0,2]
Q[6,4]=M[0,1]
H=linalg.solve(Q, P)
hxy=[H[m] for m in arange(0,int(m),1)]
xm=list(arange(1,m+1,1))
plt.figure()
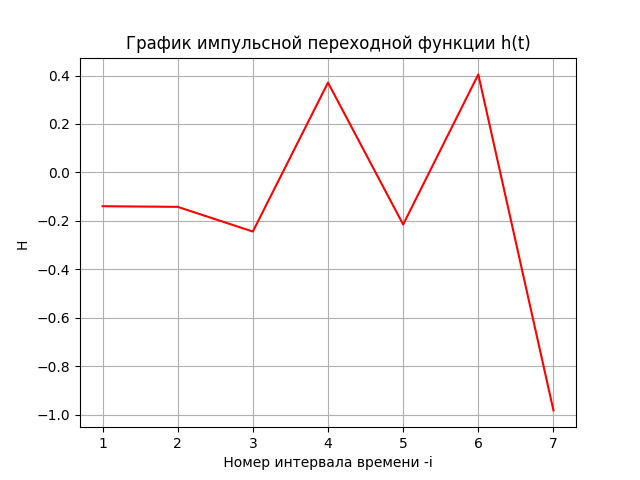
plt.title('График импульсной переходной функции h(t)')
plt.ylabel('H ')
plt.xlabel(' Номер интервала времени -i ')
plt.plot(xm, hxy, 'r')
plt.grid(True)
s1=H[0,0]/2
s2=(H[0,0]+H[1,0])/2
s3=(H[1,0]+H[2,0])/2
s4=(H[2,0]+H[3,0])/2
s5=(H[3,0]+H[4,0])/2
s6=(H[4,0]+H[5,0])/2
s7=(H[5,0]+H[6,0])/2
N=zeros([8,1])
N[0,0]=0
N[1,0]=s1
N[2,0]=N[1,0]+s2
N[3,0]=N[2,0]+s3
N[4,0]=N[3,0]+s4
N[5,0]=N[4,0]+s5
N[6,0]=N[5,0]+s6
N[7,0]=N[6,0]+s7
nxy=[N[i,0] for i in arange(0,m,1)]
xm=[i for i in arange(0,m,1)]
plt.figure()
plt.plot(xm, nxy,color='r', linewidth=3, label='Решение системы Винера-Хопфа')
var('t C1 C2')
u = Function("u")(t)
de = Eq(u.diff(t, t) +0.3*u.diff(t) + u, -0.24)
print(de)
des = dsolve(de,u)
eq1=des.rhs.subs(t,0)
eq2=des.rhs.diff(t).subs(t,0)
seq=solve([eq1,eq2],C1,C2)
rez=des.rhs.subs([(C1,seq[C1]),(C2,seq[C2])])
g= lambdify(t, rez, "numpy")
t= linspace(0,7,100)
plt.title('Динамика финансового рынка')
plt.xlabel('Номер интервала (лага) времени')
plt.ylabel('y(t), N')
plt.plot(t,g(t),color='b', linewidth=3, label='Решение ДУ финансового рынка')
plt.legend(loc='best')
plt.grid(True)
plt.show()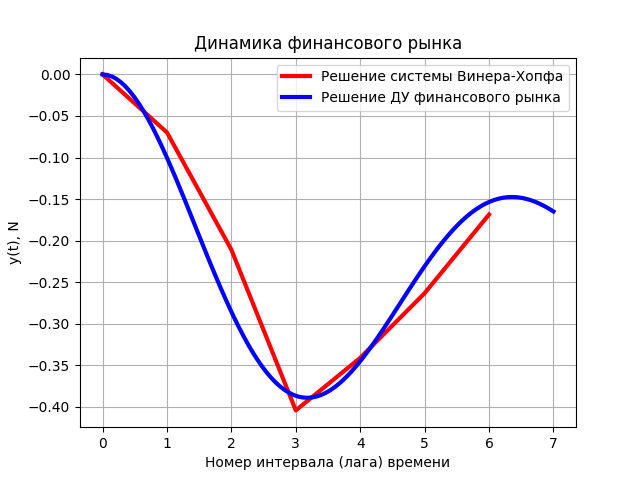
import matplotlib.pyplot as plt
from sympy import *
from numpy import (zeros,arange,ones,matrix,linalg,linspace)
"Рассчитать автокорреляционную функцию Rx (τ) и построить ее график. "
X=[797.17, 797.25, 797.15, 797.23, 797.15, 797.08, 797.05, 797.04, 797.14, 797.14, 797.1, 797.1, 797.11, 797.11, 797.11, 797.11, 797.11, 797.1, 797.1, 797.1, 797.12, 797.12, 797.12, 797.12, 797.12, 797.12, 797.1, 797.08]
n=len(X)
m=int(n/4)
Xsr=sum([w for w in X])/n
Dx=sum([(X[i]-Xsr)**2 for i in arange(0,n,1)])/(n-1)
Rxm=sum([(X[i]-Xsr)*(X[i+m]-Xsr) for i in arange(0,n-m,1)])/((n-m)*Dx)
def fRxm(m):
return sum([(X[i]-Xsr)*(X[i+m]-Xsr) for i in arange(0,n-m,1)])/((n-m)*Dx)
ym=[fRxm(m) for m in arange(0,m+1)]
xm=list(arange(0,m+1,1))
M=zeros([1,m+1])
for i in arange(0,m+1,1):
M[0,i]=fRxm(i)
plt.figure()
plt.title('График автокорреляционной функция Rx (τ). ')
plt.ylabel('Rx (τ) ')
plt.xlabel(' Номер интервала времени -m ')
plt.plot(xm, ym, 'r')
plt.grid(True)
"Рассчитать взаимокорреляционную функцию Rxy (τ) первого набора X и второго набора Y данных, построить ее график"
Y=[577.59, 622.61, 602.23, 554.64, 567.67, 635.47, 608.27, 620.82, 561.73, 639.0, 550.1, 609.31, 640.45, 611.92, 579.33, 552.04, 597.73, 553.4, 605.72, 647.94, 602.26, 610.99, 575.95, 638.99, 631.86, 589.89, 608.17, 619.26]
n=len(Y)
m=int(n/4)
Ysr=sum([w for w in Y])/n
Dy=sum([(Y[i]-Ysr)**2 for i in arange(0,n,1)])/(n-1)
Rxy=sum([(X[i]-Xsr)*(Y[i+m]-Ysr) for i in arange(0,n-m,1)])/((n-m)*Dx**0.5*Dy**0.5)
def fRxy(m):
return sum([(X[i]-Xsr)*(Y[i+m]-Ysr) for i in arange(0,n-m,1)])/((n-m)*Dx**0.5*Dy**0.5)
xy=[fRxy(m) for m in arange(0,m+1)]
plt.figure()
plt.title('График взаимокорреляционной функции Rxy (τ). ')
plt.ylabel('Rxy (τ) ')
plt.xlabel(' Номер интервала времени -m ')
plt.plot(xm, xy, 'r')
plt.grid(True)
""" Решение системы уравнений Винера-Хопфа."""
P=zeros([m,1])
for i in arange(0,m,1):
P[i,0]=fRxy(i)
Q=zeros([7,7])
for i in arange(0,7,1):
Q[0,i]=M[0,i+1]
Q[1,i]=M[0,i]
for i in arange(0,6,1):
Q[2,i+1]=M[0,i]
Q[2,0]=M[0,1]
for i in arange(0,5,1):
Q[3,i+2]=M[0,i]
Q[3,1]=M[0,1]
Q[3,0]=M[0,2]
for i in arange(0,4,1):
Q[4,i+3]=M[0,i]
Q[4,0]=M[0,3]
Q[4,1]=M[0,2]
Q[4,2]=M[0,1]
for i in arange(0,3,1):
Q[5,i+4]=M[0,i]
Q[5,0]=M[0,4]
Q[5,1]=M[0,3]
Q[5,2]=M[0,2]
Q[5,3]=M[0,1]
for i in arange(0,2,1):
Q[6,i+5]=M[0,i]
Q[6,0]=M[0,5]
Q[6,1]=M[0,4]
Q[6,2]=M[0,3]
Q[6,3]=M[0,2]
Q[6,4]=M[0,1]
H=linalg.solve(Q, P)
hxy=[H[m] for m in arange(0,int(m),1)]
xm=list(arange(1,m+1,1))
plt.figure()
plt.title('График импульсной переходной функции h(t)')
plt.ylabel('H ')
plt.xlabel(' Номер интервала времени -i ')
plt.plot(xm, hxy, 'r')
plt.grid(True)
s1=H[0,0]/2
s2=(H[0,0]+H[1,0])/2
s3=(H[1,0]+H[2,0])/2
s4=(H[2,0]+H[3,0])/2
s5=(H[3,0]+H[4,0])/2
s6=(H[4,0]+H[5,0])/2
s7=(H[5,0]+H[6,0])/2
N=zeros([8,1])
N[0,0]=0
N[1,0]=s1
N[2,0]=N[1,0]+s2
N[3,0]=N[2,0]+s3
N[4,0]=N[3,0]+s4
N[5,0]=N[4,0]+s5
N[6,0]=N[5,0]+s6
N[7,0]=N[6,0]+s7
nxy=[N[i,0] for i in arange(0,m,1)]
xm=[i for i in arange(0,m,1)]
plt.figure()
plt.plot(xm, nxy,color='r', linewidth=3, label='Решение системы Винера-Хопфа')
var('t C1 C2')
u = Function("u")(t)
de = Eq(u.diff(t, t) +0.3*u.diff(t) +u, -0.24)
print(de)
des = dsolve(de,u)
eq1=des.rhs.subs(t,0)
eq2=des.rhs.diff(t).subs(t,0)
seq=solve([eq1,eq2],C1,C2)
rez=des.rhs.subs([(C1,seq[C1]),(C2,seq[C2])])
g= lambdify(t, rez, "numpy")
t= linspace(0,7,100)
plt.title('Динамика финансового рынка')
plt.xlabel('Номер интервала (лага) времени')
plt.ylabel('y(t), N')
plt.plot(t,g(t),color='b', linewidth=3, label='Решение ДУ финансового рынка')
plt.legend(loc='best')
plt.grid(True)
plt.show()