http://habrahabr.ru/post/245801/
Здравствуй, Хабр. И сразу к делу.
Задача:
Есть два целых числа: L и R. Нужно найти максимальное значение A xor B на промежутке [L; R], где L ≤ A ≤ B ≤ R.
Казалось бы ничего сложного. Сразу напрашивается решение простым перебором.
Развернутьpublic int BruteForce(int one, int two)
{
int maxXor = 0;
while (one < two)
{
int oneTemp = one + 1;
while (oneTemp <= two)
{
int curXor = one ^ oneTemp;
if (maxXor < curXor) maxXor = curXor;
oneTemp++;
}
one++;
}
return maxXor;
}
Сложность этого решения O(n
2).
А что, если в интервале будет 1000000 чисел. Возьмем L = 1, а R = 1000001. Сколько времени понадобится cреднестатистическому компьютеру для того, чтобы посчитать максимальное значение xor на этом интервале? Моему ноутбуку потребовалось 1699914 миллисекунд.
Существует решение, которое работает значительно быстрее, именно о нем и пойдет речь в этой статье.

Основная идея.
Чтобы результирующее число было наибольшим, необходимо в как можно старшем бите этого числа получить единицу от функции xor. И так далее, по направлении к самому младшему биту. Другими словами будем последовательно работать с каждым битом результирующего числа по направлению от старших битов к младшим. Для этого очень удобно использовать структуру данных, которая называется
trie-дерево (
мне нравится как эта структура данных описана в книге Р.Сейджвика «Алгоритмы на Java»).
Trie-деревья представляют собой структуры данных, которые состоят из узлов, содержащих ссылки — или нулевые, или ссылки на другие узлы. На каждый узел указывает только один другой узел (на корневой узел не указывает ни один узел). Каждый узел содержит R ссылок, где R — размер алфавита ( в нашем случае R = 2, так как алфавит это 0 и 1). Как правило, trie-деревья содержат значительное количество нулевых ссылок, поэтому на картинках они будут опущены. Каждая ссылка соответствует очередному биту числа. Каждое целое число кодируется как путь от корня к листу.
Пример пустого trie-дерева.

Так выглядит trie-дерево после добавления 0, 1, 2, 3, 4, 5, 6, 7.
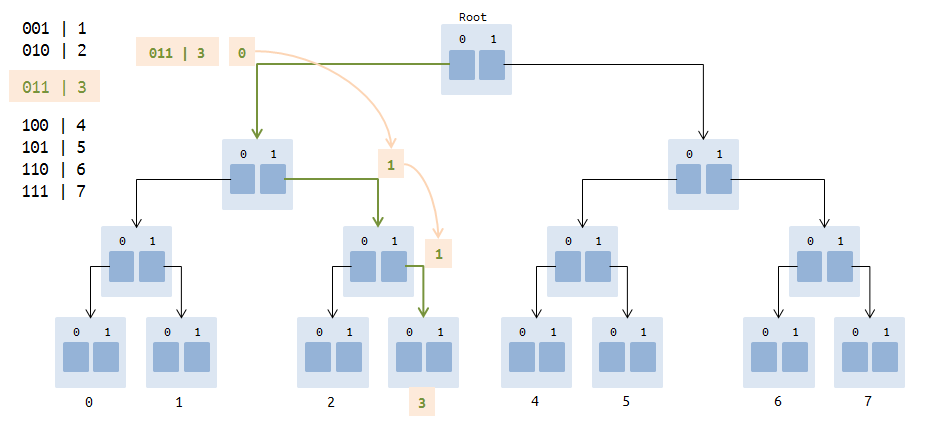
На рисунке выделен путь, состоящий из 3 ссылок —
0 ->1->1( 011 это двоичное представление числа 3).
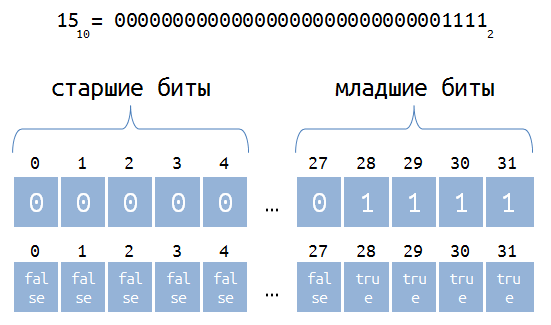
Сразу хочу пояснить, что мы будем работать только с 32-битными числами, причем старшие биты будут заполняться нулями при необходимости. Этим мы добиваемся, что числа будут храниться в массивах с одинаковой длиной. Двоичное представление целых чисел я решил хранить в массиве типа bool.
Каждый узел хранит массив ссылок на другие узлы дерева ( 2 ссылки, по одной для каждого возможного значения бита числа).
Вообще trie-дерево — это структура данных, построенная из символов строковых ключей, которая позволяет использовать символы искомого ключа для управления поиском. Строковые ключи могут быть разной длины, поэтому в каждом узле дерева дополнительно хранят значение, которое может быть нулевым или реальным значением, связанным с одним из строковых ключей. В нашем же случае, нам не обязательно хранить значение, так как ключами являются целые 32-битные числа, хранящиеся в двоичном виде в массивах одинаковой длины. Итак, trie-дерево:
using System;
namespace MaxXor
{
public class Trie
{
//for integer representation in binary system 2^32
public static readonly int MaxLengthOfBits = 32;
//size of alphabet
public static readonly int N = 2;
class Node
{
public Node[] next = new Node[Trie.N];
}
private Node _root;
}
}
Во-первых нам понадобятся функции перевода чисел из десятичной в двоичную и обратно. Тут все предельно понятно и просто. Если нужно освежить память, то можете подглядеть.
ConvertDecimalToBInaryprivate bool[] ConvertDecimalToBInary(int number)
{
int counter = Trie.MaxLengthOfBits;
bool[] result = new bool[counter];
while (number > 0)
{
result[--counter] = Convert.ToBoolean(number % 2);
number /= 2;
}
return result;
}
ConvertBinaryToDecimalprivate int ConvertBinaryToDecimal(bool[] bits)
{
int result = 0;
int base_val = 1;
for (int i = bits.Length - 1; i >= 0; i--)
{
result += Convert.ToInt32(bits[i]) * base_val;
base_val *= 2;
}
return result;
}
Во-вторых нам понадобится функция добавления целого числа в trie-дерево. Здесь остановимся по-подробнее. Для вставки в trie-дерево сначала нужно выполнить поиск нужного узла. Поиск, начинается с корня, а затем следует по ссылке, связанной с нулевым(самым старшим) битом числа; от этого узла проходит по ссылке, связанной с первым битом числа; оттуда — по ссылке, связанной со вторым битом числа; и т.д., то есть нужно просто просматривать узлы по пути от корня до некоторого узла в trie-дереве. Биты числа используются для спуска по дереву до достижения последнего бита или нулевой ссылки. Если обнаружена нулевая ссылка до выборки последнего бита числа, т.е. в trie-дереве нет узла, соответствующего последнему биту числа, то необходимо создавать узлы для каждого из отсутствующих битов.
public void AddValue(bool[] binaryNumber)
{
_root = AddValue(_root, binaryNumber, 0);
}
private Node AddValue(Node node, bool[] val, int d)
{
if (node == null) node = new Node();
//if least sagnificient bit has been added
//need return
if (d == val.Length)
{
return node;
}
// get 0 or 1 index of next array(length 2)
int index = Convert.ToInt32(val[d]);
node.next[index] = AddValue(node.next[index], val, ++d);
return node;
}
Теперь построим trie-дерево, добавив все числа из заданного промежутка.
Переходим к самому главному. Для поиска максимального значения xor, будем двигаться по trie-дереву от корня по ссылкам, то есть будем работать с битами по направлению от старших к младшим. Причем мы можем находится как в одном узле, так и в разных. При каждом проходе будем стараться получить единицу, если это возможно, от xor-а очередных битов чисел, и так далее, пока не получим все 32 бита. Получившиеся 32 бита — это и есть максимальное значение xor на нашем промежутке.
public bool[] GetMaxXor()
{
bool[] result = new bool[Trie.MaxLengthOfBits];
Node oneNode = _root, twoNode = _root;
//for each bit from most significant bit to least significant bit
for (int i = 0; i < Trie.MaxLengthOfBits; i++)
{
//getting current bit
result[i] = GetBit(oneNode, twoNode);
//go to next nodes
UpdateNodes(ref oneNode, ref twoNode);
}
return result;
}
//we need update nodes after each iteration
//we can stay on single node or split on two nodes
private void UpdateNodes(ref Node one, ref Node two)
{
if (one.Equals(two))
{
if (one.next[1] != null && one.next[0] != null)
{
two = one.next[1];
one = one.next[0];
}
else
{
one = two = ((one.next[1] != null) ? one.next[1] : one.next[0]);
}
}
else
{
if (one.next[1] != null && two.next[0] != null)
{
one = one.next[1];
two = two.next[0];
}
else if (one.next[0] != null && one.next[1] == null)
{
one = one.next[0];
two = two.next[1];
}
else
{
one = one.next[1] ?? one.next[0];
two = two.next[1] ?? two.next[0];
}
}
}
//if it's possible, we will try to get one.
private bool GetBit(Node one, Node two)
{
if (one.Equals(two))
{
// 0 xor 1 == 1; 1 xor 0 == 1
if (one.next[0] != null && one.next[1] != null) return true;
// 0 xor 0 == 0; 1 xor 1 == 0
else return false;
}
else
{
if ((one.next[1] != null && two.next[0] != null) || // 1 xor 0 == 1
(one.next[0] != null && one.next[1] == null)) // 0 xor 1 == 1
{
return true;
}
else
{// 0 xor 0 == 0; 1 xor 1 == 0
return false;
}
}
}
Пример для 3-битных чисел
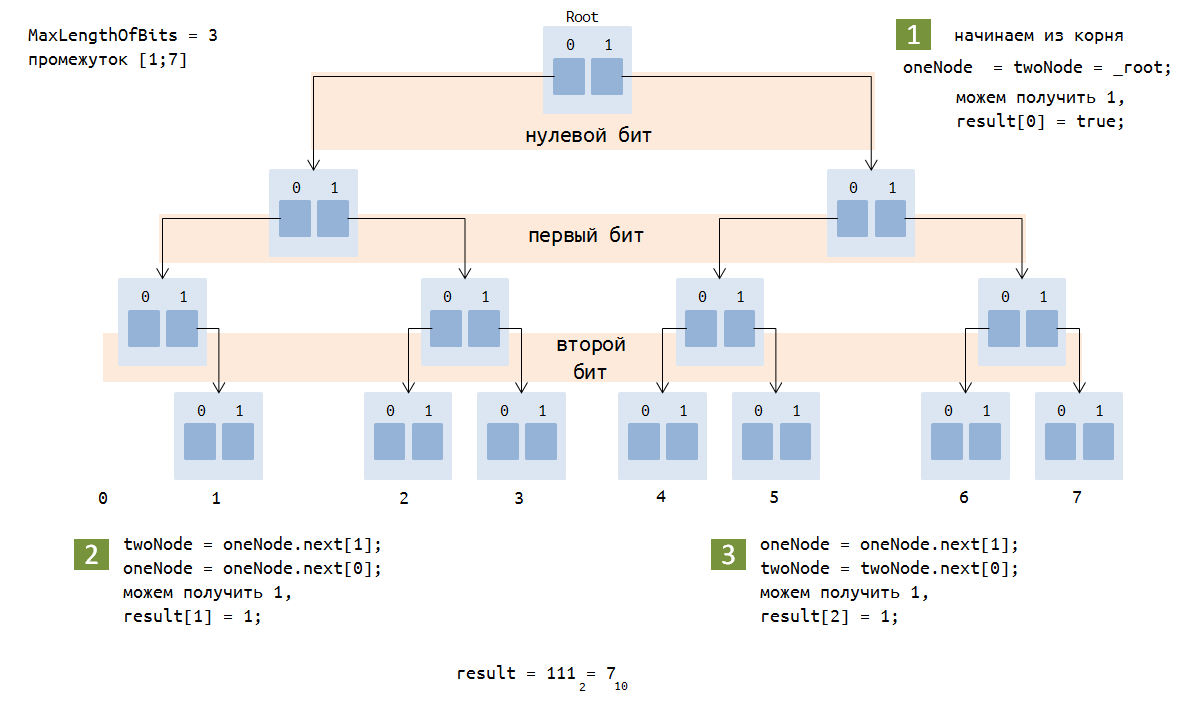
Теперь, можно сравнить время работы каждого из подходов для промежутков разной длины.
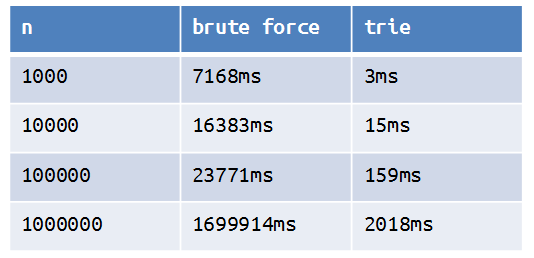
Как видно из таблицы вычисление максимального значения xor с помощью trie-дерева работает значительно быстрее. Оценка сложности алгоритма O(nlogn).
Архив с солюшеном проекта можно скачать
здесь.
P.S. Для решения данной задачи, да и вообще для хранения целых чисел в двоичном виде можно слегка упростить наше trie-дерево. Так как алфавит состоит всего из 2 символов, можно избавиться от массива и хранить просто две ссылки, например
Node left и
Node right, которые являются представлением 0 и 1 соответственно.






