https://habrahabr.ru/post/279117/- Машинное обучение
- Математика
- Python
- Data Mining
В прошлый раз мы подробно рассмотрели
многообразие линейных моделей. Теперь перейдем от теории к практике и построим самую простую, но все же полезную модель, которую вы легко сможете адаптировать к своим задачам. Модель будет проиллюстрирована кодом на R и Python, причем сразу в трех ароматах: scikit-learn, statsmodels и Patsy.
Простейшая линейная регрессия
Пусть нам даны исходные данные в виде таблицы со столбцами
x1,
x2,
x3 и
y. И мы будем строить линейную модель зависимости
y от факторов
x, то есть модель будет иметь следующий вид:
y = b0 + b1 x1 + b2 x2 + b3 x3 + ℇ
где
x,
y — исходные данные,
b — параметры модели,
ℇ — случайная величина.
Поскольку
х и
y у нас уже есть, то наша задача заключается в расчете параметров
b.
Обратите внимание, что мы ввели параметр
b0, который также называется
intercept, так как наша модельная линия совсем не обязательно будет проходить через начало координат. Если исходные данные отцентрированы, то этот параметр не требуется.
Чтобы построить модель нам также нужно ввести параметрическое предположение относительно
ℇ — без этого мы не сможем выбрать метод решения. Какой попало метод мы не имеем права применить, потому что рискуем получить сколько угодно ошибочный результат, в то время как нам требуется «достаточно хорошая» оценка параметров модели. Так что для простоты и удобства предположим, что ошибки распределены нормально, поэтому мы можем использовать метод обычных наименьших квадратов (ОНК).
Код на R# загружаем исходные данные
df <- read.csv("http://roman-kh.github.io/files/linear-models/simple1.csv")
# запускаем расчет модели
# модель glm по умолчанию включает intercept, явно его указывать в данном случае не требуется
g <- glm("y ~ x1 + x2 + x3", data=df)
# выводим коэффициенты модели
coef(g)
Код на Python: общая частьimport numpy as np
import pandas as pd
import statsmodels.api as sm
import patsy as pt
import sklearn.linear_model as lm
# загружаем файл с данными
df = pd.DataFrame.from_csv("http://roman-kh.github.io/files/linear-models/simple1.csv")
# x - таблица с исходными данными факторов (x1, x2, x3)
x = df.iloc[:,:-1]
# y - таблица с исходными данными зависимой переменной
y = df.iloc[:,-1]
Код на Python: scikit-learn# создаем пустую модель
skm = lm.LinearRegression()
# запускаем расчет параметров для указанных данных
skm.fit(x, y)
# и выведем параметры рассчитанной модели
print skm.intercept_, skm.coef_
Код на Python: statsmodels# добавим фиктивную переменную для расчета intercept'а
x_ = sm.add_constant(x)
# создаем модель для метода обычных наименьших квадратов (Ordinary Least Squares)
smm = sm.OLS(y, x_)
# запускаем расчет модели
res = smm.fit()
# теперь выведем параметры рассчитанной модели
print res.params
Код на Python: statsmodels с формуламиПереходя с R на Python, многие начинают со statsmodels, потому что в ней есть привычные R'овские формулы:
# создаем модель на основе формулы
smm = sm.OLS.from_formula("y ~ x1 + x2 + x3", data=df)
# запускаем расчет модели
res = smm.fit()
# теперь выведем параметры рассчитанной модели
print res.params
Код на Python: Patsy + numpyБлагодаря библиотеке Patsy вы легко можете использовать R-подобные формулы в любой своей программе:
# создаем матрицу факторов и результатов из формулы и исходного датафрейма
pt_y, pt_x = pt.dmatrices("y ~ x1 + x2 + x3", df)
# вызываем стандартную numpy'вскую процедуру оптимизации по МНК
# кстати, именно ее и вызывает LinearRegression из scikit-learn для неразреженной матрицы с исходными данными
# а для разреженной вызывается scipy.sparse.linalg.lsqr
res = np.linalg.lstsq(pt_x, pt_y)
# достаем коэффициенты модели
b = res[0].ravel()
print b
Обратите внимание, что все способы расчета коэффициентов дают один и тот же результат. И это совершенно не случайно. Вследствие нормальности ошибок оптимизируемый функционал (ОНК, OLS) оказывается выпуклым, а значит имеет единственный минимум, и искомый набор коэффициентов модели также будет единственным.
Однако даже незначительное изменение исходных данных, несмотря на сохранение формы распределений, приведет к изменению коэффициентов. Проще говоря, хотя реальная жизнь не меняется, и природа данных также остается неизменной, в результате неизменной методики расчета вы будете получать разные модели, а ведь по идее модель должна быть единственной. Подробнее об этом мы поговорим в статье про регуляризацию.
Изучаем данные
Итак, мы уже построили модель… Однако скорее всего мы допустили ошибку, возможно даже и не одну. Поскольку мы не изучили данные, прежде чем браться за модель, то получили модель непонятно чего. Поэтому давайте все же заглянем в данные и посмотрим что там есть.
Как вы помните, в исходной таблице было 4 столбца:
x1,
x2,
x3 и
y. И мы построили регрессионную зависимость
y от всех
x. Поскольку мы не можем одним взглядом сразу охватить весь 4-мерный гиперкуб, то посмотрим на отдельные графики
x-y.
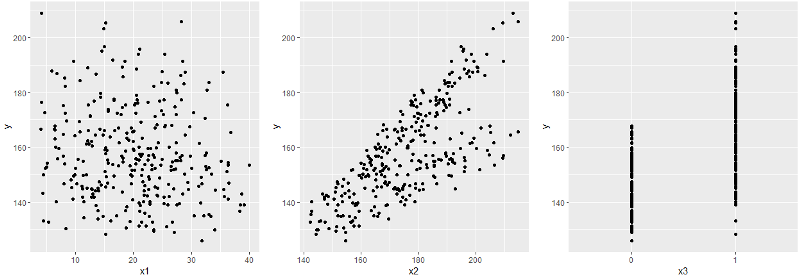
Сразу бросается в глаза
x3 — бинарный признак — а с ними стоит быть повнимательнее. В частности, имеет смысл взглянуть на совместное распределение остальных
x вместе с
x3.
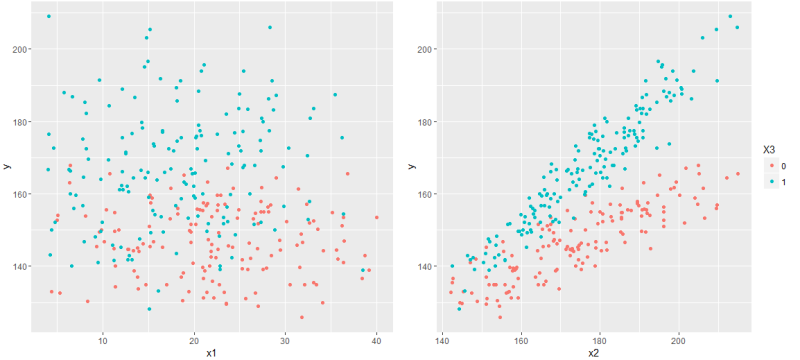
Теперь пришло время отобразить график, соответствующий построенной модели. И тут стоит обратить внимание, что наша линейная модель — это вовсе не линия, а гиперплоскость, поэтому на двумерном графике мы сможем отобразить только отдельный срез этой модельной гиперплоскости. Проще говоря, чтобы показать график модели в координатах
x1-
y надо зафиксировать значения
x2 и
x3, а, меняя их, получим бесконечное множество графиков — и все они будут графиками модели (а точнее проекцией на плоскость
x1-
y).
Поскольку
x3 — бинарный признак — можно показать отдельную линию для каждого значения признака, а
x1 и
x2 зафиксировать на уровне среднего арифметического, то есть нарисуем графики y=f(x1 | x2=E(x2)) и y=f(x2 | x1=E(x1)), где E — среднее арифметическое по всем значениям x1 и x2 соответственно.
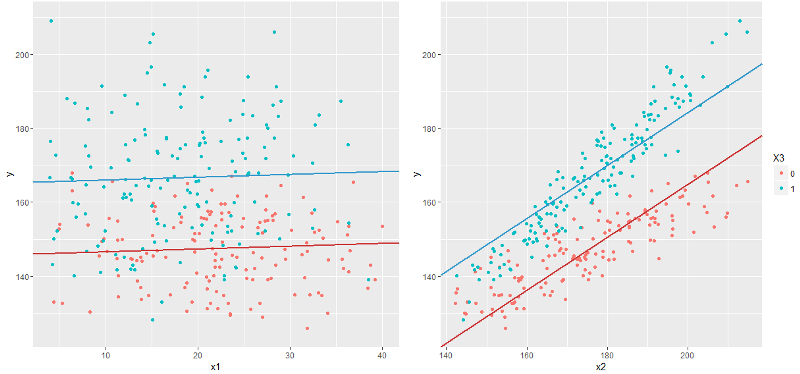
И сразу бросается в глаза, что график
y~x2 выглядит как-то неправильно. Помня, что построенная модель должна предсказывать математическое ожидание
y, тут мы видим, что модельная линия как раз математическому ожиданию совсем не сооветствует: например в начале графика голубые точки реальных значений находятся ниже голубой линии, а в конце — выше, причем у красной линии все наоборот, хотя обе линии должны проходить примерно посредине облака точек.
Приглядевшись внимательнее, можно догадаться, что голубая и красная линии должны быть даже непараллельны. Как же это сделать в линейной модели? Очевидно, что построив линейную модель
у=f(x1,x2,x3) мы можем получить бесконечное количество линий вида
y=f(x2 | x1,x3), то есть зафиксировав две из трех переменных. Так, в частности, получены красная линия
у=f(x2 | x1=E(x), x3=0) и голубая
у=f(x2 | x1=E(x), x3=1) на правом графике. Однако, все подобные линии будут параллельны.
Непараллельная линейная модель
Чтобы внести в модель непараллельность, немного усложним ее, добавив всего одно слагаемое:
y = b0 + b1 x1 + b2 x2 + b3 x3 + b4 x2 x3 + ℇ
К чему это приведет? Раньше любая линия на графике
y~x2 имела один и тот же наклон, задаваемый коэффициентом
b2. Теперь же в зависимости от значения
x3 линия будет иметь наклон
b2 (для
x3=0) или
b2+b4 (для
x3=1).
Код на R# загружаем исходные данные
df <- read.csv("http://roman-kh.github.io/files/linear-models/simple1.csv")
# запускаем расчет модели
# модель glm по умолчанию включает intercept, явно его указывать в данном случае не требуется
g <- glm("y ~ x1 + x2 + x3 + x2*x3", data=df)
# выводим коэффициенты модели
coef(g)
Код на Python: общая частьimport numpy as np
import pandas as pd
import statsmodels.api as sm
import patsy as pt
import sklearn.linear_model as lm
# загружаем файл с данными
df = pd.DataFrame.from_csv("http://roman-kh.github.io/files/linear-models/simple1.csv")
# x - таблица с исходными данными факторов (x1, x2, x3)
x = df.iloc[:,:-1]
# y - таблица с исходными данными зависимой переменной
y = df.iloc[:,-1]
Код на Python: scikit-learn# создаем новый фактор
x["x4"] = x["x2"] * x["x3"]
# создаем пустую модель
skm = lm.LinearRegression()
# запускаем расчет параметров для указанных данных
skm.fit(x, y)
# и выведем параметры рассчитанной модели
print skm.intercept_, skm.coef_
Код на Python: statsmodels# создаем новый фактор
x["x4"] = x["x2"] * x["x3"]
# добавим фиктивную переменную для расчета intercept'а
x_ = sm.add_constant(x)
# создаем модель для метода обычных наименьших квадратов (Ordinary Least Squares)
smm = sm.OLS(y, x_)
# запускаем расчет модели
res = smm.fit()
# теперь выведем параметры рассчитанной модели
print res.params
Код на Python: statsmodels с формуламиПереходя с R на Python, многие начинают со statsmodels, потому что в ней есть привычные R'овские формулы:
# создаем модель на основе формулы
smm = sm.OLS.from_formula("y ~ x1 + x2 + x3 + x2*x3", data=df)
# запускаем расчет модели
res = smm.fit()
# теперь выведем параметры рассчитанной модели
print res.params
Код на Python: Patsy + numpyБлагодаря библиотеке Patsy вы легко можете использовать R-подобные формулы в любой своей программе:
# создаем матрицу факторов и результатов из формулы и исходного датафрейма
pt_y, pt_x = pt.dmatrices("y ~ x1 + x2 + x3 + x2*x3", df)
# вызываем стандартную numpy'вскую процедуру оптимизации по МНК
# кстати, именно ее и вызывает LinearRegression из scikit-learn для неразреженной матрицы с исходными данными
# а для разреженной вызывается scipy.sparse.linalg.lsqr
res = np.linalg.lstsq(pt_x, pt_y)
# достаем коэффициенты модели
b = res[0].ravel()
print b
А теперь взглянем на обновленный график.
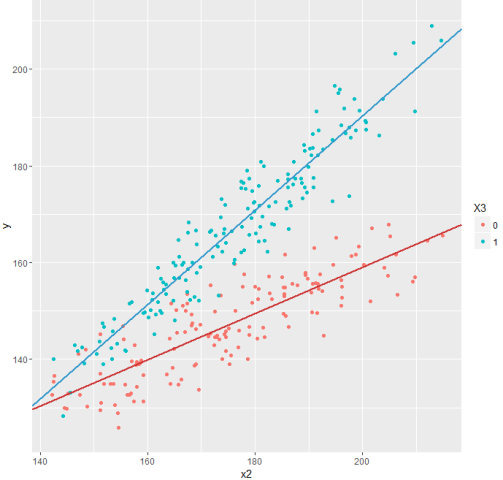
Гораздо лучше!
Этот прием — перемножение переменных — чрезвычайно полезен для бинарных и категорийный факторов и позволяет в рамках одной модели по сути построить сразу несколько моделей, отражающих особенности разных групп исследуемых объектов (мужчин и женщин, рядовых сотрудников и менеджеров, любителей классической, рок или поп-музыки). Особенно интересные модели можно получить, когда в исходных данных есть несколько бинарных и категорийных факторов.
По просьбам желающих я также создал небольшой
ipython notebook.
Подводим итог: мы построили пусть простую, но все же весьма адекватную модель, которая, судя по графикам, неплохо отражает реальные данные. Однако, все эти «весьма» и «неплохо» лучше представить в измеримых величинах. А также пока остается непонятным, насколько построенная модель устойчива к небольшим изменениям в исходных данных или к структуре этих данных (в частности, к взаимозависимости между факторами). К этим вопросам мы обязательно вернемся.



