https://habr.com/ru/post/460445/

• Open source
• Python
• Алгоритмы
• Математика
• Matlab

Всем привет!

Часто ко мне обращаются люди с вопросами по задачам из области цифровой обработки сигналов (ЦОС). Я подробно рассказываю нюансы, подсказываю нужные источники информации. Но всем слушателям, как показало время, не хватает практических задач и примеров в процессе познания этой области. В связи с этим я решил написать краткий интерактивный курс по цифровой обработке сигналов и выложить его в открытый доступ.

Большая часть обучающего материала для наглядного и интерактивного представления реализована с использованием Jupyter Notebook. Предполагается, что читатель имеет базовые знания из области высшей математики, а также немного владеет языком программирования Python.

Список лекций

Этот курс содержит материалы в виде законченных лекций по разным тематикам из области цифровой обработки сигналов. Материалы представлены с использованием библиотек на языке Python (пакеты numpy, scipy, matplotlib, и т.д.). Основная информация для этого курса взята из моих лекций, которые я, будучи аспирантом, читал студентам Московского Энергетического Института (НИУ МЭИ). Частично информация из этих лекций была использована на обучающих семинарах в Центре Современной Электроники, где я выступал в качестве лектора. Кроме того, в этот материал входит перевод различных научных статей, компиляция информации из достоверных источников и литературы по тематике цифровой обработки сигналов, а также официальная документация по прикладным пакетам и встроенным функциям библиотек scipy и numpy языка Python.

Для пользователей MATLAB (GNU Octave) освоение материала с точки зрения программного кода не составит труда, поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из Python-библиотек.

Все материалы сгруппированы по основным тематикам цифровой обработки сигналов:

1. Сигналы: аналоговые, дискретные, цифровые. Z-преобразование,
2. Преобразование Фурье: амплитудный и фазовый сигнала, ДПФ и БПФ,
3. Свертка и корреляция. Линейная и циклическая свертка. Быстрая свёртка
4. Случайные процессы. Белый шум. Функция плотности вероятностей
5. Детерминированные сигналы. Модуляция: АМ, ЧМ, ФМ, ЛЧМ. Манипуляция
6. Фильтрация сигналов: БИХ, КИХ фильтры
7. Оконные функции в задачах фильтрации. Детектирование слабых сигналов.
8. Ресемплинг: децимация и интерполяция. CIC-фильтры, фильтры скользящего среднего

Список лекций — достаточный но, разумеется, неполный для вводного знакомства с областью ЦОС. При наличии свободного времени я планирую поддерживать и развивать этот проект.

Где найти?

Все материалы — абсолютно бесплатны и доступны в виде открытого репозитория на моем гитхабе как opensource проект. Материалы представлены в двух форматах — в виде тетрадок Jupyter Notebook для интерактивной работы, изучения и редактирования, и в виде скомпилированных из этих тетрадок HTML-файлов (после скачивания с гитхаба имеют вполне пригодный формат для чтения и для печати).

Ниже приводится очень краткое описание разделов курса с небольшими пояснениями, терминами и определениями. Основная информация доступна в исходных лекциях, здесь представлен лишь краткий обзор!

Сигналы. Z-преобразование

Вводный раздел, в котором содержится основная информация по типам сигналов. Вводится понятие дискретной последовательности, дельта-функции и функции Хевисайда (единичный скачок).

Все сигналы по способу представления на множестве можно разделить на четыре группы:

• аналоговые — описываются непрерывными во времени функциями,
• дискретные — прерываются во времени с шагом заданным дискретизации,
• квантованные — имеют набор конечных уровней (как правило, по амплитуде),
• цифровые — комбинация свойств дискретных и квантованных сигналов.

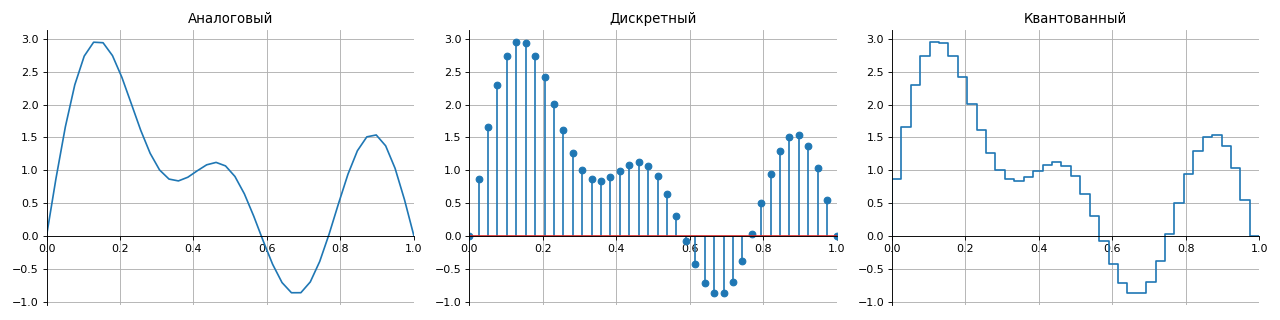
Для правильного восстановления аналогового сигнала из цифрового без искажений и потерь используется теорема отсчетов, известная как Теорема Котельникова (Найквиста-Шеннона).

Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой строго больше удвоенной верхней частоты спектра непрерывного сигнала.

Если шаг квантования и дискретизации выбраны неправильно, преобразование сигнала из аналоговой формы в дискретную будет происходить с искажениями.

Также в этом разделе описывается Z-преобразование и его свойства, показывается представление дискретных последовательностей в Z-форме.

Пример конечной дискретной последовательности:

x(nT) = {2, 1, -2, 0, 2, 3, 1, 0}

.
Пример этой же последовательности в Z-форме:

X(z) = 2 + z^-1 — 2z^-2 + 2z^-4 + 3z^-5 + 1z^-6

Преобразование Фурье. Свойства. ДПФ и БПФ

В этом разделе описывается понятие временной и частотной области сигнала. Вводится определение дискретного преобразования Фурье (ДПФ). Рассмотрены прямое и обратное ДПФ, их основные свойства. Показан переход от ДПФ к алгоритму быстрого преобразования Фурье (БПФ) по основанию 2 (алгоритмы децимации по частоте и по времени). Отражена эффективность БПФ в сравнении с ДПФ.

В частности, в этом разделе описывается Python пакет scipy.ffpack для вычисления различных преобразований Фурье (синусное, косинусное, прямое, обратное, многомерное, вещественное).

Преобразование Фурье позволяет представить любую функцию в виде набора гармонических сигналов! Преобразование Фурье лежит в основе методов свертки и проектировании цифровых корреляторов, активно применяется при спектральном анализе, используется при работе с длинными числами.

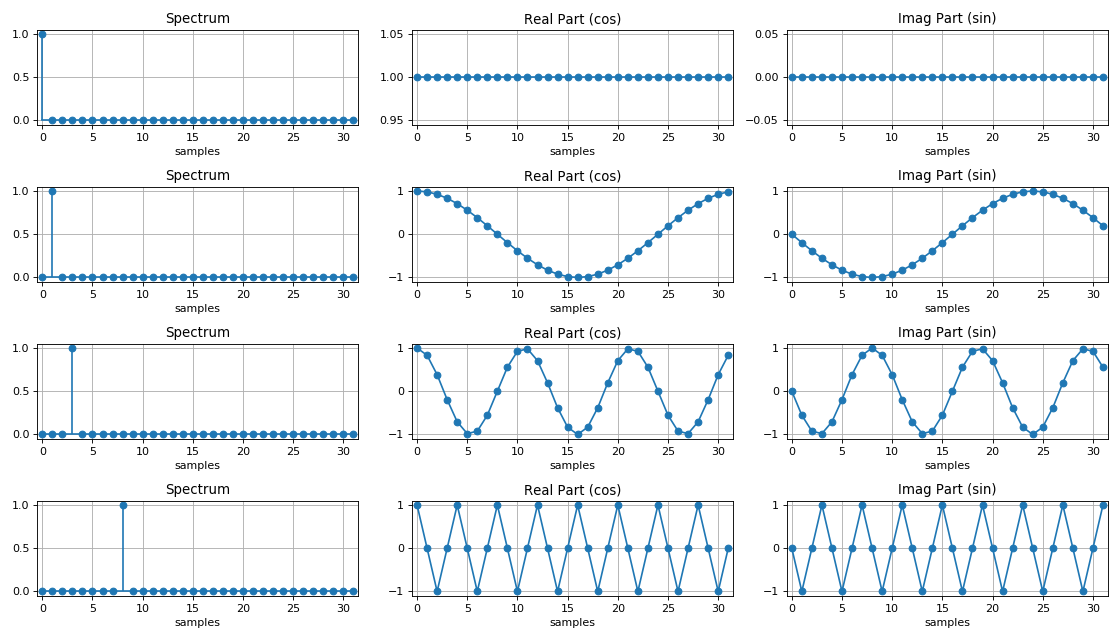
Особенности спектров дискретных сигналов:
1. Спектральная плотность дискретного сигнала – периодическая функция с периодом, равным частоте дискретизации.
2. Если дискретная последовательность вещественная, то модуль спектральной плотности такой последовательности есть четная функция, а аргумент – нечетная функция частоты.

Спектр гармонического сигнала:

Сравнение эффективности ДПФ и БПФ

Эффективность алгоритма БПФ и количество выполняемых операций линейно зависит от длины последовательности N:


Как видно, чем больше длина преобразования, тем больше экономия вычислительных ресурсов (по скорости обработки или количеству аппаратных блоков)!

Любой сигнал произвольной формы можно представить в виде набора гармонических сигналов разных частот. Иными словами, сигнал сложной формы во временной области имеет набор комплексных отсчетов в частотной области, которые называются *гармоники*. Эти отсчеты выражают амплитуду и фазу гармонического воздействия на определенной частоте. Чем больше набор гармоник в частотной области, тем точнее представляется сигнал сложной формы.

Свертка и корреляция

В этом разделе вводится понятие корреляции и свертки для дискретных случайных и детерминированных последовательностей. Показана связь автокорреляционной и взаимнокорреляционной функций со сверткой. Описываются свойства свертки, в частности, рассмотрены методы линейной и циклической свертки дискретного сигнала с подробным разбором на примере дискретной последовательности. Кроме того, показан метод вычисления «быстрой» свертки с помощью алгоритмов БПФ.

В реальных задачах часто ставится вопрос о степени похожести одного процесса на другой или же о независимости одного процесса от другого. Иными словами, требуется определить взаимосвязь между сигналами, то есть найти корреляцию. Методы корреляции используются в широком диапазоне задач: поиск сигналов, компьютерное зрение и обработка изображений, в задачах радиолокации для определения характеристик целей и определения расстояния до объекта. Кроме того, с помощью корреляции производится поиск слабых сигналов в шумах.

Свертка описывает взаимодействие сигналов между собой. Если один из сигналов — импульсная характеристика фильтра, то свертка входной последовательности с импульсной характеристикой есть ни что иное, как реакция цепи на входное воздействие. Иными словами, результирующий сигнал отражает прохождение сигнала через фильтр.

Автокорреляционная функция (АКФ) находит применение в кодировании информации. Выбор кодирующей последовательности по параметрам длины, частоты и формы во многом обусловлен корреляционными свойствами этой последовательности. Наилучшая кодовая последовательность обладает наименьшим значением вероятности ложного обнаружения или срабатывания (для детектирования сигналов, для пороговых устройств) или ложной синхронизации (для передачи и приема кодовых последовательностей).

В этом разделе представлена таблица сравнения эффективности быстрой свертки и свертки, вычисляемой по прямой формуле (по числу вещественных умножений).

Как видно, для длин БПФ до 64, быстрая свёртка проигрывает у прямого метода. Однако, при увеличении длины БПФ результаты меняются в обратную сторону — быстрая свертка начинает выигрывать у прямого метода. Очевидно, чем больше длина БПФ, тем лучше выигрыш частотного метода.

Случайные сигналы и шум

В этом разделе вводится понятие случайных сигналов, плотности распределения вероятностей, закона распределения случайной величины. Рассматриваются математические моменты — среднее (математическое ожидание) и дисперсия (среднеквадратическое отклонение). Также в этом разделе рассматривается нормальное распределение и связанное с ним понятие белого шума, как основного источника шумов (помех) при обработке сигналов.

Случайным сигналом называют функцию времени, значения которой заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью. К основным характеристикам случайных сигналов относятся:

• закон распределения (относительное время пребывания значения сигнала в определенном интервале),
• спектральное распределение мощности сигнала.

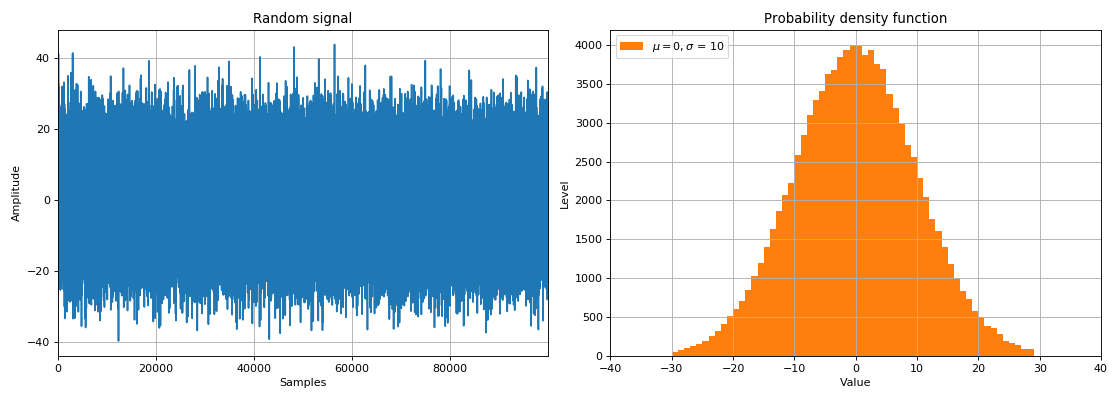
В задачах ЦОС случайные сигналы делятся на два класса:

• шумы — беспорядочные колебания, состоящие из набора разных частот и амплитуд,
• сигналы, несущие информацию, для обработки которых требуется прибегать к вероятностным методам.

С помощью случайных величин можно моделировать воздействие реальной среды на прохождение сигнала от источника к приёмнику данных. При прохождении сигнала через какое-то шумящее звено, к сигналу добавляется так называемый белый шум. Как правило, спектральная плотность такого шума равномерно (одинаково) распределена на всех частотах, а значения шума во временной области распределены нормально (Гауссовский закон распределения). Поскольку белый шум физически добавляется к амплитудам сигнала в выбранные отсчеты времени, он называется аддитивный белый гауссовский шум (AWGN — Additive white Gaussian noise).

Сигналы, модуляция и манипуляция

В этом разделе показаны основные способы изменения одного или нескольких параметров гармонического сигнала. Вводятся понятия амплитудной, частотной и фазовой модуляции. В частности, выделяется линейная частотная модуляция, применяемая в задачах радиолокации. Показаны основные характеристики сигналов, спектры модулированных сигналов в зависимости от параметров модуляции.



Для удобства на языке Python создан набор функций, осуществляющих перечисленные виды модуляции. Пример реализации ЛЧМ-сигнала:

def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs):
    """
    Create Chirp signal

    Parameters
    ----------
    amp : float
        Signal magnitude
    beta : float
        Modulation bandwidth: beta < N for complex, beta < 0.5N for real
    freq : float or int
        Linear frequency of signal
    period : integer
        Number of points for signal (same as period)
    kwargs : bool
        Complex signal if is_complex = True
        Modulated by half-sine wave if is_modsine = True
    """
    is_complex = kwargs.get('is_complex', False)
    is_modsine = kwargs.get('is_modsine', False)

    t = np.linspace(0, 1, period)
    tt = np.pi * (freq * t + beta * t ** 2)
    
    if is_complex is True:
        res = amp * (np.cos(tt) + 1j * np.sin(tt))
    else:
        res = amp * np.cos(tt)

    if is_modsine is True:
        return res * np.sin(np.pi * t)
    return res

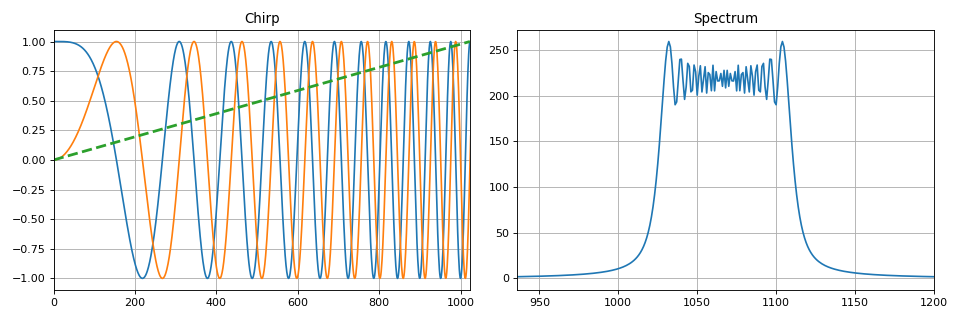
Также в этом разделе из теории передачи дискретных сообщений описаны виды цифровой модуляции — манипуляции. Как и в случае с аналоговыми сигналами, цифровые гармонические последовательности могут быть манипулированы по амплитуде, фазе и частоте (либо по нескольким параметрам сразу).

Цифровые фильтры — БИХ и КИХ

Достаточно большой раздел, посвященный вопросам цифровой фильтрации дискретных последовательностей. В задачах цифровой обработки сигналов данные проходят через цепи, которые называются фильтрами. Цифровые фильтры, как и аналоговые, обладают различными характеристиками — частотные: АЧХ, ФЧХ, временная: импульсная характеристика, а также передаточная характеристика фильтра. Цифровые фильтры используются в основном для улучшения качества сигнала — для выделения сигнала из последовательности данных, либо для ухудшения нежелательных сигналов — для подавления определенных сигналов в приходящих последовательностях отсчетов.



В разделе перечислены основные преимущества и недостатки цифровых фильтров (в сравнении с аналоговыми). Вводится понятие импульсной и передаточной характеристик фильтра. Рассматривается два класса фильтров — с бесконечной импульсной характеристикой (БИХ) и конечной импульсной характеристикой (КИХ). Показан способ проектирования фильтров по канонической и прямой форме. Для КИХ фильтров рассматривается вопрос о способе перехода к рекурсивной форме.



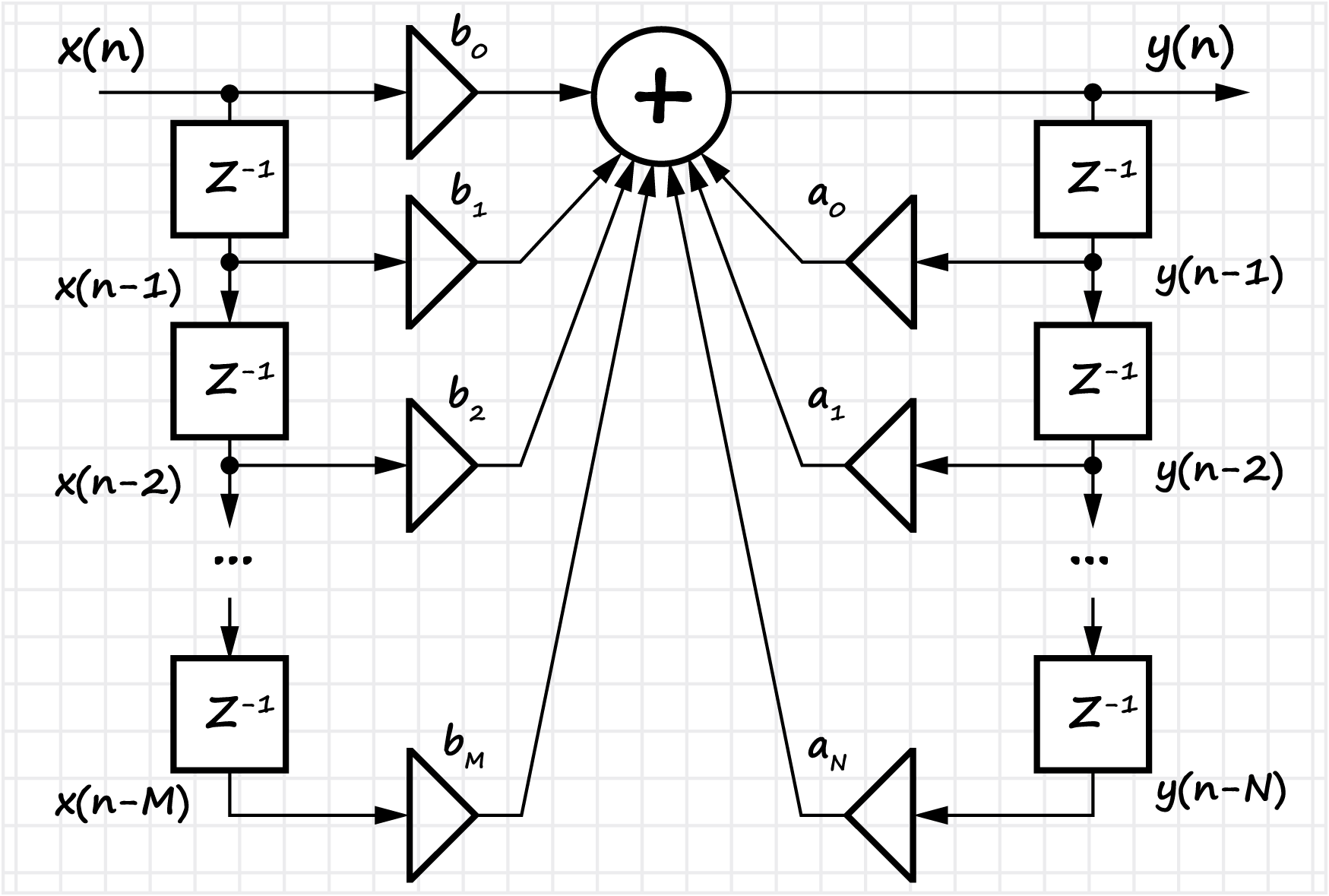
Для КИХ фильтров показан процесс проектирования фильтра от стадии разработки технического задания (с указанием основных параметров), до программной и аппаратной реализации — поиска коэффициентов фильтра (с учетом формы представления числа, разрядности данных и т.д.). Вводятся определения симметричных КИХ фильтров, линейной ФЧХ и её связи с понятием групповой задержки.

Оконные функции в задачах фильтрации

В задачах цифровой обработки сигналов используются оконные функции различной формы, которые при наложении на сигнал во временной области, позволяют качественно улучшить его спектральные характеристики. Большое количество всевозможных окон обусловлено в первую очередь одной из главных особенностей любого оконного наложения. Эта особенность выражается во взаимосвязи уровня боковых лепестков и ширины центрального лепестка. Правило:

Чем сильнее подавление боковых лепестков спектра, тем шире главный лепесток спектра и наоборот.

Одно из применений оконных функций: обнаружение слабых сигналов на фоне более сильных путём подавления уровня боковых лепестков. Основные оконные функции в задачах ЦОС — **треугольное, синусоидальное, окно Ланцоша, Ханна, Хэмминга, Блэкмана, Харриса, Блэкмана-Харриса, окно с плоской вершиной, окно Наталла, Гаусса, Кайзера** и множество других. Большая часть из них выражена через конечный ряд путём суммирования гармонических сигналов с определенными весовыми коэффициентами. Такие сигналы отлично реализуются на практике на любых аппаратных устройствах (программируемые логические схемы или сигнальные процессоры).

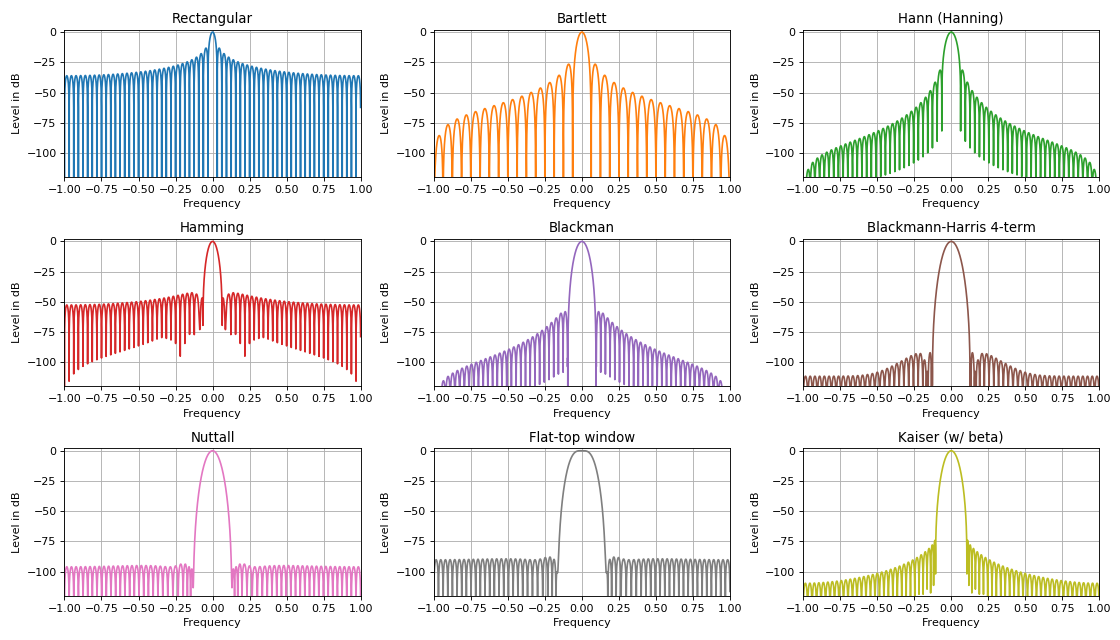
Ресемплинг. Децимация и интерполяция

В этом разделе рассматриваются вопросы многоскоростной обработки сигналов — изменения частоты дискретизации. Многоскоростная обработка сигналов (multirate processing) предполагает, что в процессе линейного преобразования цифровых сигналов возможно изменение частоты дискретизации в сторону уменьшения или увеличения, либо в дробное число раз. Это приводит к более эффективной обработке сигналов, так как открывается возможность использования минимально допустимых частот дискретизации и, как следствие, значительного уменьшения требуемой вычислительной производительности проектируемой цифровой системы.

Децимация (прореживание) – понижение частоты дискретизации. Интерполяция – повышение частоты дискретизации.

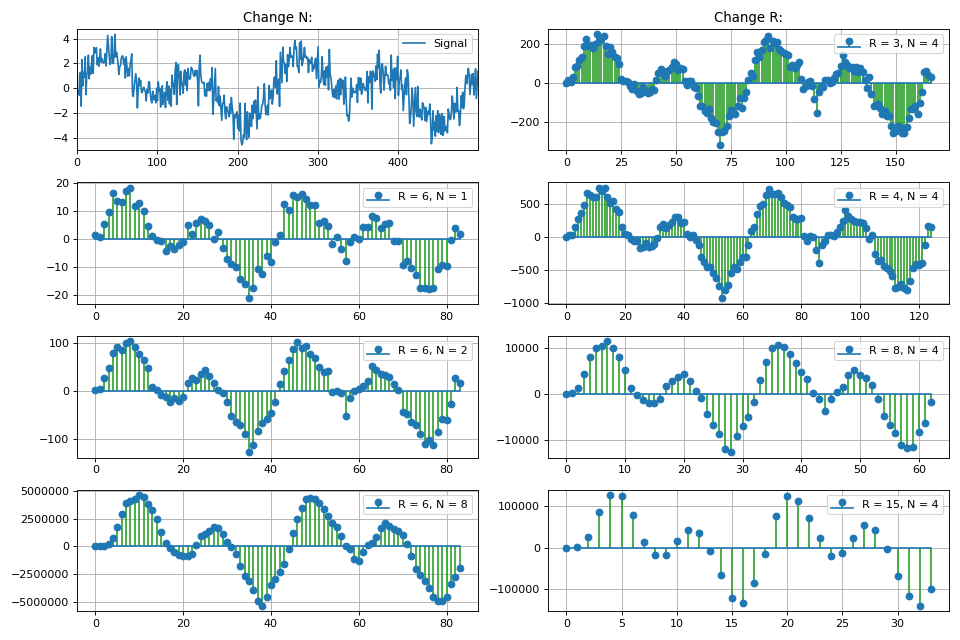
Также в разделе рассматривается класс однородных КИХ фильтров, которые называются интегрально-гребенчатыми фильтрами (CIC, Cascaded integrator–comb). Показана реализация, основные свойства и особенности CIC фильтров. В силу линейности математических операций, происходящих в CIC фильтре возможно каскадное соединение нескольких фильтров подряд, что дает пропорциональное уменьшение уровня боковых лепестков, но также увеличивает «завал» главного лепестка амплитудно-частотной характеристики.



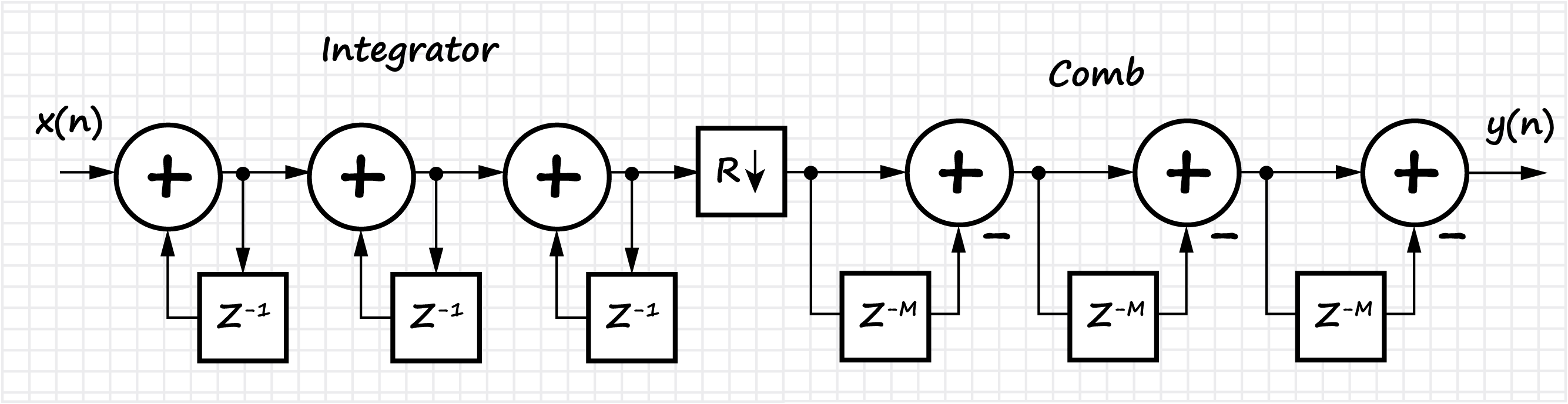
График АЧХ фильтра в зависимости от коэффициента децимации:



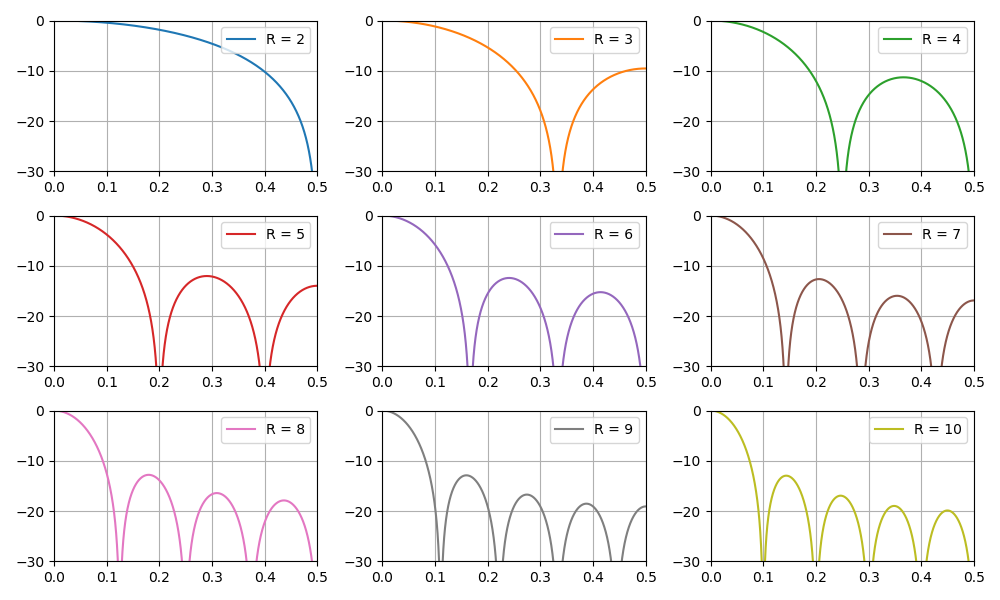
Также в этом разделе обсуждается вопрос увеличения разрядности данных на выходе CIC фильтра в зависимости от его параметров. Это особенно важно в задачах программной реализации, в частности на ПЛИС.

Для практической реализации CIC фильтров на Python разработан отдельный класс CicFilter, реализующий методы децимации и интерполяции. Также показаны примеры изменения частоты дискретизации с помощью встроенных методов из scipy пакета Python.





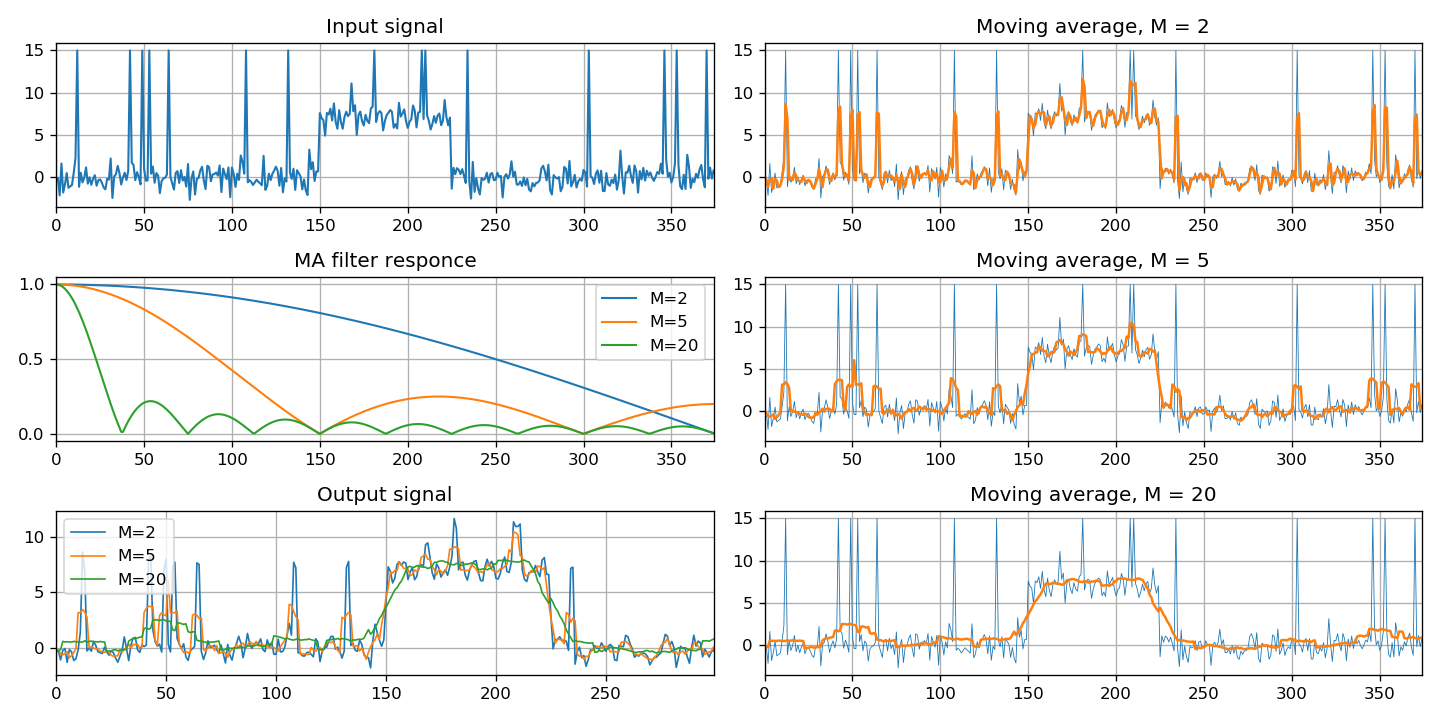
Наконец, в этом разделе приведен особый класс фильтров — скользящего среднего. Показано три способа реализации: через свертку сигналов, с помощью КИХ-фильтра и БИХ-фильтра.

Заключение

Надеюсь, этот курс лекций в совокупности с моими предыдущими статьями по цифровой обработке сигналов на ПЛИС принесет практическую пользу и поможет читателю лучше понять основы цифровой обработки сигналов. Этот проект будет улучшаться и дополняться новым полезным и не менее интересным материалом. Следите за развитием!

Дополнительно к этому материалу я поддерживаю и развиваю свой проект по основным модулям ЦОС (на языке Python). Он содержит пакет генерации различных сигналов, класс CIC фильтров для задач децимации и интерполяции, алгоритм расчета коэффициентов корректирующего КИХ-фильтра, фильтр скользящего среднего, алгоритм вычисления сверх-длинного БПФ через методы двумерного преобразования (последнее очень пригодилось в работе при аппаратной реализации на ПЛИС).

Спасибо за внимание!