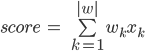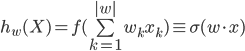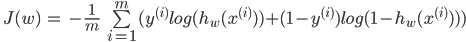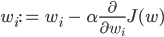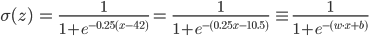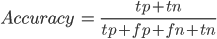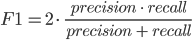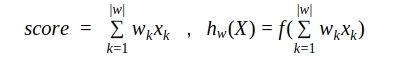Краткий курс машинного обучения или как создать нейронную сеть для решения скоринг задачи

вторник, 24 октября 2017 г. в 03:12:55

Программирование
Машинное обучение
Алгоритмы
Python
Data Mining

Мы часто слышим такие словесные конструкции, как «машинное обучение», «нейронные сети». Эти выражения уже плотно вошли в общественное сознание и чаще всего ассоциируются с распознаванием образов и речи, с генерацией человекоподобного текста. На самом деле алгоритмы машинного обучения могут решать множество различных типов задач, в том числе помогать малому бизнесу, интернет-изданию, да чему угодно. В этой статье я расскажу как создать нейросеть, которая способна решить реальную бизнес-задачу по созданию скоринговой модели. Мы рассмотрим все этапы: от подготовки данных до создания модели и оценки ее качества.

Вопросы, которые разобраны в статье:

• Как собрать и подготовить данные для построения модели?
• Что такое нейронная сеть и как она устроена?
• Как написать свою нейронную сеть с нуля?
• Как правильно обучить нейронную сеть на имеющихся данных?
• Как интерпретировать модель и ее результаты?
• Как корректно оценить качество модели?

«Вопрос о том, может ли компьютер думать, не более интересен,
чем вопрос о том, может ли субмарина плавать».
Эдсгер Вибе Дейкстра

Во многих компаниях, менеджеры по продажам общаются с потенциальными клиентами, проводят им демонстрации, рассказывают о продукте. Отдают, так сказать, свою душу по сотому разу на растерзание тем, кто, возможно, попал в их руки совершенно случайно. Часто клиенты недостаточно понимают, что им нужно, или то, что продукт может им дать. Общение с такими клиентами не приносит ни удовольствия, ни прибыли. А самое неприятное то, что из-за ограничения по времени, можно не уделить достаточно внимания действительно важному клиенту и упустить сделку.

Я математик-программист в сервисе seo-аналитики Serpstat. Недавно я получил интересную задачу по улучшению уже существующей и работающей у нас скоринговой модели, по-новому оценив факторы, которые влияют на успех продажи. Скоринг считался на основе анкетирования наших клиентов, и каждый пункт, в зависимости от ответа на вопрос, вносил определенное количество очков в суммарный балл. Все эти баллы за разные вопросы расставлялись на основе статистических гипотез. Скоринговая модель использовалась, время шло, данные собирались и в один прекрасный день попали ко мне. Теперь, когда у меня появилась достаточная выборка, можно было смело строить гипотезы, используя алгоритмы машинного обучения.

Я расскажу вам, как мы построили свою скоринг модель. Это реальный кейс с реальными данными, со всеми трудностями и ограничениями, с которыми мы столкнулись в реальном бизнесе. Итак, обо всем по порядку.

Мы подробно остановимся на всех этапах работы:

▸ Сбор данных
▸ Препроцессинг
▸ Построение модели
▸ Анализ качества и интерпретация модели

Рассмотрим устройство, создание и обучение нейросети. Все это я описываю, решая реальную скоринговую задачу, и постоянно подкрепляю новую теорию примером.

Сбор данных

Вначале нужно понять, какие вопросы будут представлять клиента (или просто объект) в будущей модели. К задаче подходим серьезно, так как на ее основании строится дальнейший процесс. Во-первых, нужно не упустить важные признаки, описывающие объект, во-вторых, создать жесткие критерии для принятия решения о признаке. Основываясь на опыте, я могу выделить три категории вопросов:

Булевы (бикатегориальные), ответом на которые является: Да или Нет (1 или 0). Например, ответ на вопрос: есть ли у клиента аккаунт?
Категориальные, ответом на которые является конкретный класс. Обычно классов больше двух (мультикатегориальные), иначе вопрос можно свести к булевому. Например, цвет: красный, зеленый или синий.
Количественные, ответами на которые являются числа, характеризующее конкретную меру. Например, количество обращений в месяц: пятнадцать.

Зачем я так подробно останавливаюсь на этом? Обычно, когда рассматривают классическую задачу, решаемую алгоритмами машинного обучения, мы имеем дело только с численными данными. Например, распознавание черно-белых рукописных цифр с картинки 20 на 20 пикселей. В этом примере 400 чисел (описывающих яркость черно-белого пикселя) представляют один пример из выборки. В общем случае данные необязательно должны быть числовыми. Дело в том, что при построении модели нужно понимать, с какими типами вопросов алгоритм может иметь дело. Например: дерево принятия решения обучается на всех типах вопросов, а нейросеть принимает только числовые входные данные и обучается лишь на количественных признаках. Означает ли это, что мы должны отказаться от некоторых вопросов в угоду более совершенной модели? Вовсе нет, просто нужно правильно подготовить данные.

Данные должны иметь следующую классическую структуру: вектор признаков для каждого i-го клиента X⁽ⁱ⁾ = {x⁽ⁱ⁾₁, x⁽ⁱ⁾₂, ..., x⁽ⁱ⁾_n} и класс Y⁽ⁱ⁾ — категория, показывающая купил он или нет. Например: клиент⁽³⁾ = {зеленый, горький, 4.14, да} — купил.

Основываясь на вышесказанном, попробуем представить формат данных с типами вопросов, для дальнейшей подготовки:

класс: (категория)	цвет: (категория)	вкус: (категория)	вес: (число)	твердый: (bool)
-	красный	кислый	4.23	да
-	зеленый	горький	3.15	нет
+	зеленый	горький	4.14	да
+	синий	сладкий	4.38	нет
-	зеленый	соленый	3.62	нет

Таблица 1 — Пример данных обучающей выборки до препроцессинга

Препроцессинг

После того как данные собраны, их необходимо подготовить. Этот этап называется препроцессинг. Основная задача препроцессинга — отображение данных в формат пригодный для обучения модели. Можно выделить три основных манипуляции над данными на этапе препроцессинга:

Создание векторного пространства признаков, где будут жить примеры обучающей выборки. По сути, это процесс приведения всех данных в числовую форму. Это избавляет нас от категорийных, булевых и прочих не числовых типов.
Нормализация данных. Процесс, при котором мы добиваемся, например того, чтобы среднее значение каждого признака по всем данным было нулевым, а дисперсия — единичной. Вот самый классический пример нормализации данных: X = (X — μ)/σ
функция нормализации
```
def normalize(X):
    return (X-X.mean())/X.std()
```
Изменение размерности векторного пространства. Если векторное пространство признаков слишком велико (миллионы признаков) или мало (менее десятка), то можно применить методы повышения или понижения размерности пространства:
- Для повышения размерности можно использовать часть обучающей выборки как опорные точки, добавив в вектор признаков расстояние до этих точек. Этот метод часто приводит к тому, что в пространствах более высокой размерности множества становятся линейно разделимыми, и это упрощает задачу классификации.
- Для понижения размерности чаще всего используют PCA. Основная задача метода главных компонент — поиск новых линейных комбинаций признаков, вдоль которых максимизируется дисперсия значений проекций элементов обучающей выборки.

Одним из важнейших трюков в построении векторного пространства — метод представления в виде числа категориальных и булевых типов. Встречайте: One-Hot (рус. Унитарный Код). Основная идея такой кодировки — это представление категориального признака, как вектора в векторном пространстве размерностью, соответствующей количеству возможных категорий. При этом значение координаты этой категории берется за единицу, а все остальные координаты обнуляются. С булевыми значениями все совсем просто, они превращаются в вещественные единицы или нули.

Например, элемент выборки может быть или горьким, или сладким, или соленым, или кислым, или умами (мясным). Тогда One-Hot кодировка будет следующей: горький = (1, 0, 0, 0 ,0), сладкий = (0, 1, 0, 0 ,0), соленый = (0, 0, 1, 0 ,0), кислый = (0, 0, 0, 1 ,0), умами = (0, 0, 0, 0, 1). Если у вас возник вопрос почему вкусов пять, а не четыре, то ознакомьтесь с этой статьей о вкусовой сенсорной системе, ну а к скорингу это никакого отношения не имеет, и мы будем использовать четыре, ограничившись старой классификацией.

Теперь мы научились превращать категориальные признаки в обычные числовые вектора, а это очень полезно. Проведя все манипуляции над данными, мы получим обучающую выборку, подходящую любой модели. В нашем случае, после применения унитарной кодировки и нормализации данные выглядят так:

class:	red:	green:	blue:	bitter:	sweet:	salti:	sour:	weight:	solid:
0	1	0	0	0	0	0	1	0.23	1
0	0	1	0	1	0	0	0	-0.85	0
1	0	1	0	1	0	0	0	0.14	1
1	0	0	1	0	1	0	0	0.38	0
0	0	1	0	0	0	1	0	-0.48	0

Таблица 2 — Пример данных обучающей выборки после препроцессинга

Можно сказать, что препроцессинг — это процесс отображения понятных нам данных в менее удобную для человека, но зато в излюбленную машинами форму.

Формула скоринга чаще всего представляет из себя следующую линейную модель:

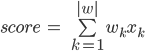
Где, k — это номер вопроса в анкете, w_k — коэффициент вклада ответа на этот k-ый вопрос в суммарный скоринг, |w| — количество вопросов (или коэффициентов), x_k — ответ на этот вопрос. При этом вопросы могут быть любыми, как мы и обсуждали: булевыми(да или нет, 1 или 0), числовыми (например, рост = 175) или категориальными, но представленными в виде унитарной кодировки (зеленый из перечня: красный, зеленый или синий = [0, 1, 0]). При этом можно считать, что категориальные вопросы распадаются на столько булевых, сколько категорий присутствует в вариантах ответа (например: клиент красный? клиент зеленый? клиент синий?).

Выбор модели

Теперь самое важное: выбор модели. На сегодняшний день существует множество алгоритмов машинного обучения, на основе которых можно построить скоринг модель: Decision Tree (дерево принятия решений), KNN (метод k-ближайших соседей), SVM (метод опорных векторов), NN (нейросеть), CNN (сверточная нейросеть). И выбор модели стоит основывать на том, чего мы от нее хотим. Во-первых, насколько решения, повлиявшие на результаты модели, должны быть понятными. Другими словами, насколько нам важно иметь возможность интерпретировать структуру модели.

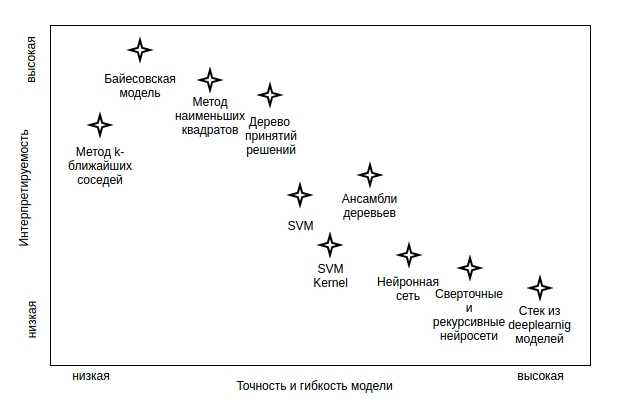Рис. 1 — Зависимость гибкости алгоритма машинного обучения и интерпретируемости полученной модели

Кроме того, не все модели легко построить, для некоторых требуются весьма специфические навыки и очень-очень мощное железо. Но самое важное — это внедрение построенной модели. Бывает так, что бизнес-процесс уже налажен, и внедрение какой-то сложной модели попросту невозможно. Или требуется именно линейная модель, в которой клиенты, отвечая на вопросы, получают положительные или отрицательные баллы в зависимости от варианта ответа. Иногда, напротив, есть возможность внедрения, и даже требуется сложная модель, учитывающая очень неочевидные сочетания входных параметров, находящая взаимосвязи между ними. Итак, что же выбрать?

В выборе алгоритма машинного обучения мы остановились на нейронной сети. Почему? Во-первых, сейчас существует много крутых фреймворков, таких как TensorFlow, Theano. Они дают возможность очень глубоко и серьезно настраивать архитектуру и параметры обучения. Во-вторых, возможность менять устройство модели от однослойной нейронной сети, которая, кстати, неплохо интерпретируема, до многослойной, обладающей отличной способностью находить нелинейные зависимости, меняя при этом всего пару строчек кода. К тому же, обученную однослойную нейросеть можно превратить в классическую аддитивную скоринг модель, складывающую баллы за ответы на разные вопросы анкетирования, но об этом чуть позже.

Теперь немного теории. Если для вас такие вещи, как нейрон, функция активации, функция потери, градиентный спуск и метод обратного распространения ошибки — родные слова, то можете смело это все пропускать. Если нет, добро пожаловать в краткий курс искусственных нейросетей.

Краткий курс искусственных нейронных сетей

Начнем с того, что искусственные нейронные сети (ИНС) — это математические модели организации реальных биологических нейронных сетей (БНС). Но в отличие от математических моделей БНС, ИНС не требует точное описание всех химических и физических процессов, таких как описание «поджигания» потенциала действия (ПД), работы нейромедиаторов, ионных каналов, вторичных посредников, белков транспортеров и пр. От ИНС требуется схожесть с работой реальных БНС только на функциональном, а не на физическом уровне.

Базовый элемент нейросети — нейрон. Попробуем составить самую простую функциональную математическую модель нейрона. Для этого опишем в общих чертах функционирование биологического нейрона.

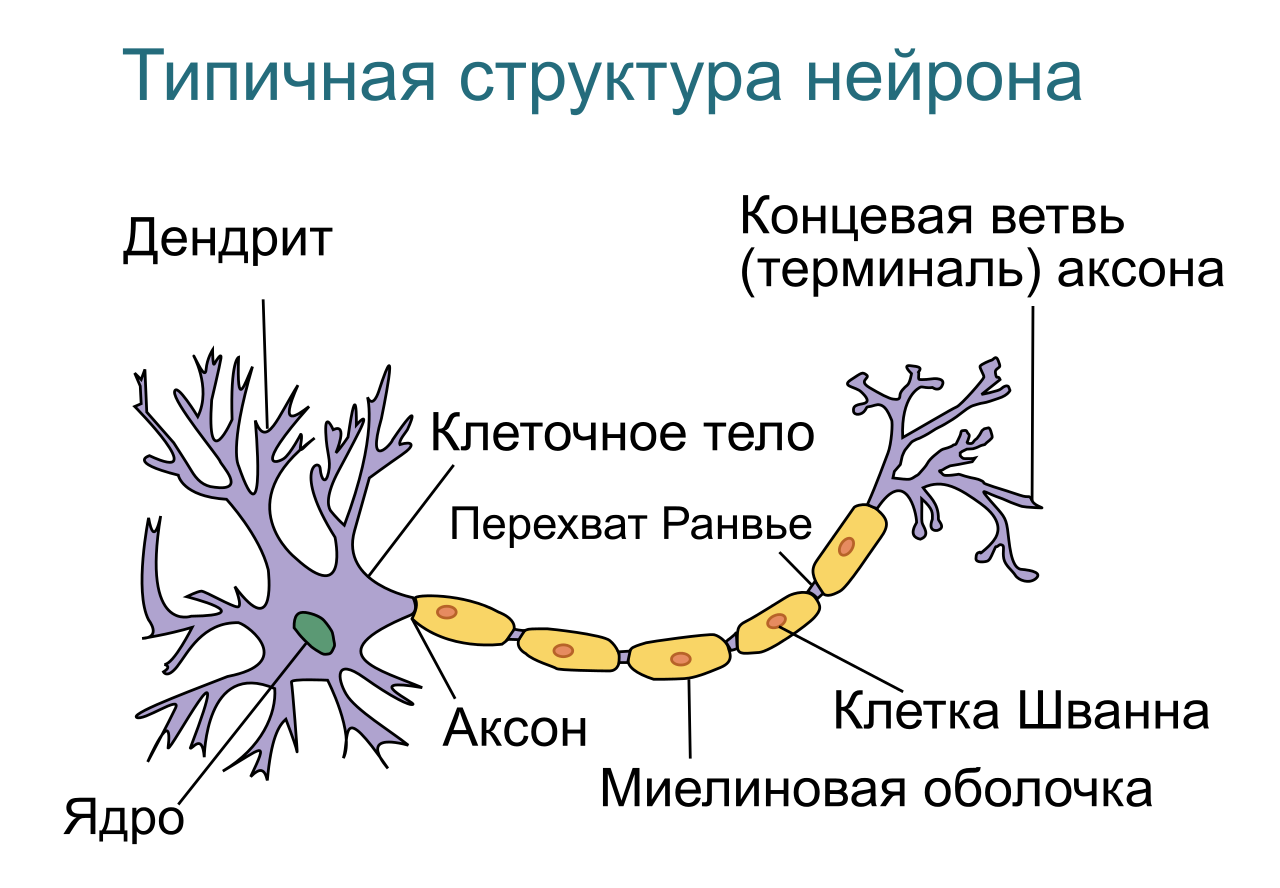Рис. 2 — Типичная структура биологического нейрона

Как мы видим, структуру биологического нейрона можно упростить до следующей: дендриты, тело нейрона и аксон. Дендриты — ветвящиеся отростки, собирающие информацию со входа в нейрон (это может быть внешняя информация с рецепторов, например с колбочки в случае цвета или внутренняя информация от другого нейрона). В том случае, если входящая информация активировала нейрон (в биологическом случае — потенциал стал выше какого-то порога), рождается волна возбуждения (ПД), которая распространяется по мембране тела нейрона, а затем через аксон, посредством выброса нейромедиатора, передает сигнал другим нервным клетками или тканям.

Основываясь на этом, Уоррен Мак-Каллок и Уолтер Питтс в 1943 году предложили модель математического нейрона. А в 1958 году Френк Розенблатт на основе нейрона Мак-Каллока-Питтса создал компьютерную программу, а затем и физическое устройство — перцептрон. С этого и началась история искусственных нейронных сетей. Теперь рассмотрим структурную модель нейрона, с которым мы будем иметь дело дальше.

Рис. 3 — Модель математического нейрона Мак-Каллока-Питтса

Где:

X — входной вектор параметров. Вектор (столбец) чисел (биол. степень активации разных рецепторов), пришедших на вход нейрону.
W — вектор весов (в общем случае — матрица весов), числовые значение, которые меняются в процессе обучения (биол. обучение на основе синаптической пластичности, нейрон учится правильно реагировать на сигналы с его рецепторов).
Сумматор — функциональный блок нейрона, который складывает все входные параметры умноженные на соответствующие им веса.
Функция активации нейрона — есть зависимость значения выхода нейрона от значения пришедшего от сумматора.
Следующие нейроны, куда на один из множества их собственных входов подается значение с выхода данного нейрона (этот слой может отсутствовать, если этот нейрон последний, терминальный).

реализация математического нейрона

import numpy as np

def neuron(x, w):
    z = np.dot(w, x)
    output = activation(z)
    return output

Затем из этих минимальных структурных единиц собирают классические искусственные нейронные сети. Принята следующая терминология:

Входной (рецепторный) слой — это вектор параметров (признаков). Этот слой не состоит из нейронов. Можно сказать, что это цифровая информация, снятая рецепторами из «внешнего» мира. В нашем случае это информация о клиенте. Слой содержит столько элементов, сколько входных параметров (плюс bias-term нужный для сдвига порога активации).
Ассоциативный (скрытый) слой — глубинная структура, способная к запоминанию примеров, нахождению сложных корреляций и нелинейных зависимостей, к построению абстракций и обобщений. В общем случае это даже не слой, а множество слоев между входными и выходными. Можно сказать, что каждый слой подготавливает новый (более высокоуровневый) вектор признаков для следующего слоя. Именно этот слой отвечает за появление в процессе обучения высокоуровневых абстракций. Структура содержит столько нейронов и слоев, сколько душе угодно, а может и вообще отсутствовать (в случае классификации линейно разделимых множеств).
Выходной слой — это слой, каждый нейрон которого отвечает за конкретный класс. Выход этого слоя можно интерпретировать как функцию распределения вероятности принадлежности объекта разным классам. Слой содержит столько нейронов, сколько классов представлено в обучающей выборке. Если класса два, то можно использовать два выходных нейрона или ограничиться всего одним. В таком случае один нейрон по-прежнему отвечает только за один класс, но если он выдает значения близкие к нулю, то элемент выборки по его логике должен принадлежать другому классу.

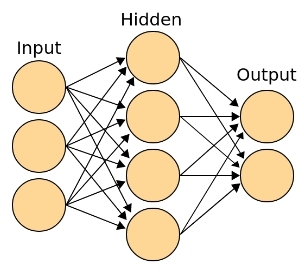Рис. 4 — Классическая топология нейросети, со входным (рецепторным), выходным, принимающим решение о классе, и ассоциативным (скрытым) слоем

Именно благодаря наличию скрытых ассоциативных слоев, искусственная нейронная сеть способна строить гипотезы, основанные на нахождении сложных зависимостей. Например, для сверточных нейросетей, распознающих изображения, на входной слой будут подаваться значения яркости пикселей изображения, а выходной слой будет содержать нейроны, отвечающие за конкретные классы (человек, машина, дерево, дом и т. д.) В процессе обучения в близких к «рецепторам» скрытых слоях начнут «сами собой» появляться (специализироваться) нейроны, возбуждающиеся от прямых линий, разного угла наклона, затем реагирующие на углы, квадраты, окружности, примитивные паттерны: чередующиеся полоски, геометрические сетчатые орнаменты. Ближе к выходным слоям — нейроны, реагирующие, например, на глаз, колесо, нос, крыло, лист, лицо и т. д.

Рис. 5 — Образование иерархических ассоциаций в процессе обучения сверточной нейронной сети

Проводя биологическую аналогию, хочется сослаться на слова замечательного нейрофизиолога Вячеслава Альбертовича Дубынина, касающиеся речевой модели:

«Наш мозг способен создавать, генерировать такие слова, которые обобщают слова более низкого уровня. Скажем, зайчик, мячик, кубики, кукла ― игрушки; игрушки, одежда, мебель ― это предметы; а предметы, дома, люди ― это объекты окружающей среды. И так еще немного, и мы дойдем до абстрактных философских понятий, математических, физических. То есть речевое обобщение ― это очень важное свойство нашей ассоциативной теменной коры, и оно, вдобавок, многоуровневое и позволяет речевую модель внешнего мира формировать, как целостность. В какой-то момент оказывается, что нервные импульсы способны очень активно двигаться по этой речевой модели, и это движение мы и называем гордым словом «мышление».

Много теории?! Но есть и хорошие новости: в самом простом случае вся нейросеть может быть представлена одним единственным нейроном! При этом даже один нейрон часто хорошо справляется с задачей, особенно, когда дело касается распознавания класса объекта в пространстве, в котором объекты этих классов являются линейно сепарабельными. Часто добиться линейно сепарабельности можно повысив размерность пространства, о чем было написано выше, и ограничиться всего одним нейроном. Но иногда проще добавить в нейросеть пару скрытых слоев и не требовать от выборки линейной сепарабельности.

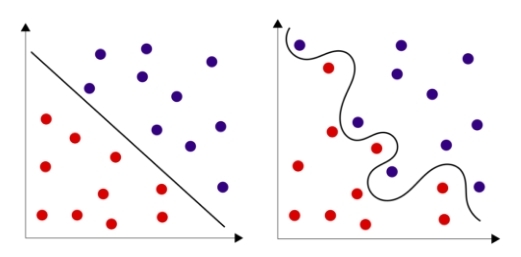Рис. 6 — Линейно разделимые множества и линейно неразделимые множества

Ну а теперь давайте опишем все это формально. На входе нейрона мы имеем вектор параметров. В нашем случае это результаты анкетирования клиента, представленные в числовой форме X⁽ⁱ⁾ = {x⁽ⁱ⁾₁, x⁽ⁱ⁾₂, ..., x⁽ⁱ⁾_n}. При этом каждому клиенту сопоставлен Y⁽ⁱ⁾ — класс, характеризующий успешность лида (1 или 0). Нейросеть, по сути, должна найти оптимальную разделяющую гиперповерхность в векторном пространстве, размерность которого соответствует количеству признаков. Обучение нейронной сети в таком случае — нахождение таких значений (коэффициентов) матрицы весов W, при которых нейрон, отвечающий за класс, будет выдавать значения близкие к единице в тех случаях, если клиент купит, и значения близкие к нулю, если нет.

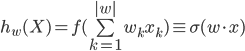
Как видно из формулы, результат работы нейрона — это функция активации (часто обозначаемая через ) от суммы произведения входных параметров на искомые в процессе обучения коэффициенты. Разберемся что же такое функция активации.

Так как на вход нейросети могут поступать любые действительные значения, и коэффициенты матрицы весов тоже могут быть какими угодно, то и результатом суммы их произведений может быть любое вещественное число от минус до плюс бесконечности. У каждого элемента обучающей выборки есть значение класса относительно этого нейрона (ноль или один). Желательно получить от нейрона значение в этом же диапазоне от нуля до единицы, и принять решение о классе, в зависимости от того, к чему это значение ближе. Еще лучше интерпретировать это значение как вероятность того, что элемент относится к этому классу. Значит, нам нужна такая монотонная гладкая функция, которая будет отображать элементы из множества вещественных чисел в область от нуля до единицы. На эту должность отлично подходит так называемая сигмоида.

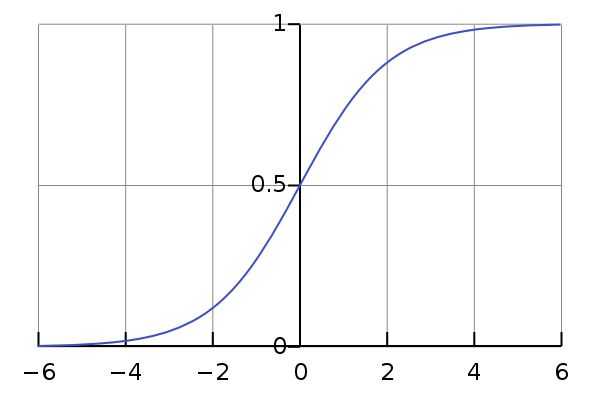Рис. 7 — График логистической кривой, одной из самых классических представительниц класса сигмоид

функция активации

def activation(z):
    return 1/(1+np.exp(-z))

Кстати, в реальных биологических нейронах такая непрерывная функция активации не реализовалась. В наших с вами клетках существует потенциал покоя, который составляет в среднем -70mV. Если на нейрон подается информация, то активированный рецептор, открывает сопряженные с ним ионные каналы, что приводит к повышению или понижению потенциала в клетке. Можно провести аналогию между силой реакции на активацию рецептора и полученным в процессе обучения одним коэффициентом матрицы весов. Как только потенциал достигает значения в -50mV, возникает ПД, и волна возбуждения доходит по аксону до пресинаптического окончания, выбрасывая нейромедиатор в межсинаптическую среду. То есть реальная биологическая активация — ступенчатая, а не гладкая: нейрон либо активировался, либо нет. Это показывает, насколько мы математически свободны в построении наших моделей. Взяв у природы основной принцип распределенного вычисления и обучения, мы способны построить вычислительный граф, состоящий из элементов, обладающих любыми желаемыми свойствами. В нашем примере мы желаем получать от нейрона континуальные, а не дискретные значения. Хотя в общем случае функция активации может быть и другой.

Вот самое важное, что стоит извлечь из написанного выше: «Обучение нейросети (синаптическое обучение) должно свестись к оптимальному подбору коэффициентов матрицы весов с целью минимизации допускаемой ошибки.» В случае однослойной нейросети эти коэффициенты можно интерпретировать как вклад параметров элемента в вероятность принадлежности к конкретному классу.

Результат работы нейросети принято называть гипотезой (англ. hypothesis). Обозначают через h(X), показывая зависимость гипотезы от входных признаков (параметров) объекта. Почему гипотезой? Так уж исторически сложилось. Лично мне этот термин нравится. В итоге мы хотим, чтобы гипотезы нейросети как можно больше соответствовали действительности (реальным классам объектов). Собственно здесь и рождается основная идея обучения на опыте. Теперь нам потребуется мера, описывающая качество нейросети. Этот функционал обычно называют «функцией потерь» (англ. loss function). Функционал обычно обозначают через J(W), показывая его зависимость от коэффициентов матрицы весов. Чем функционал меньше, тем реже наша нейросеть ошибается и тем это лучше. Именно к минимизации этого функционала и сводится обучение. В зависимости от коэффициентов матрицы весов нейросеть может иметь разную точность. Процесс обучения — это движение по гиперповерхности функционала потери, целью которого является минимизация этого функционала.

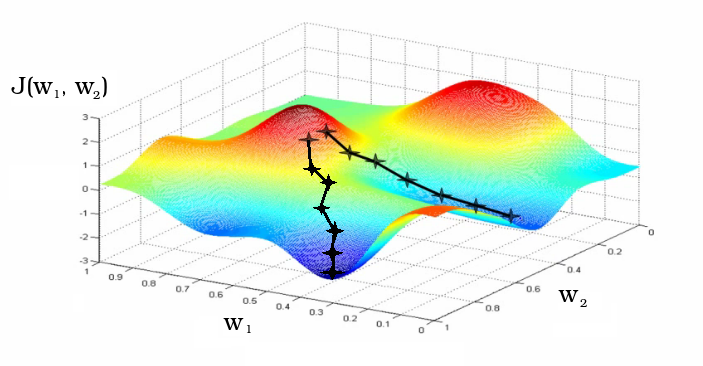Рис. 8 — Процесс обучения, как градиентный спуск к локальному минимуму функционала потери

Обычно коэффициенты матрицы весов инициализируются случайным образом. В процессе обучения коэффициенты меняются. На графике показаны два разных итерационных пути обучения как изменение коэффициентов w₁ и w₂ матрицы весов нейросети, проинициализированных в соседстве.

Теперь собственно о том, как обучить нейросеть. Для этого существует множество вариантов, но я расскажу о двух: эволюционный (генетический) алгоритм и метод градиентного спуска. Оба этих метода используются. Эволюционные алгоритмы — это направление в искусственном интеллекте, которое основывается на моделировании естественного отбора. Эволюционный метод обучения очень прост в понимании, и с него лучше начинать новичкам. Сейчас он используется в основном для тренировки глубинных слоев нейросети. Метод градиентного спуска и обратного распространения ошибки более сложный, но зато один из самых эффективных и популярных методов обучения.

Эволюционное обучение

В рамках этого метода оперируем следующей терминологией: коэффициенты матрицы весов — геном, один коэффициент — ген, «перевернутая вниз головой» функция потерь — ландшафт приспособленности (тут мы уже ищем локальный максимум, но это всего лишь условность). Этот метод и вправду очень простой. После того как мы выбрали топологию (устройство) нейросети, необходимо сделать следующее:

Проинициализировать геном (матрицу весов) случайным образом в диапазоне от -1 до 1. Повторить это несколько раз, тем самым создав начальную популяцию разных, но случайных нейросетей. Размер популяции обозначим через P — population or parents.
случайная инициализация коэффициентов матрицы весов
```
import random

def generate_population(p, w_size):
    population = []
    for i in range(p):
        model = []
        for j in range(w_size + 1): # +1 for b (bias term)
            model.append(2 * random.random() - 1)  # random initialization from -1 to 1 for b and w
        population.append(model)
    return np.array(population)
```
Создать нескольких потомков. Например, три-четыре клона каждого родителя, внеся небольшие изменения (мутации) в их геном. Например: переназначить случайным образом половину весов, или добавить случайным образом к половине весов случайные значения в диапазоне от -0.1 до 0.1.
реализация мутагенеза
```
def mutation(genom, t=0.5, m=0.1):
    mutant = []
    for gen in genom:
        if random.random() <= t:
            gen += m*(2*random.random() -1)
        mutant.append(gen)
    return mutant
```
Оценить приспособленность каждого потомка, на основе того, как он справляется с примерами из обучающей выборки (в самом простом варианте — процент верно угаданных классов, в идеале — перевернутая функция потерь). Отсортировать потомков по их приспособленности.
простейшая оценка приспособленности
```
def accuracy(X, Y, model):
    A = 0
    m = len(Y)
    for i, y in enumerate(Y):
        A += (1/m)*(y*(1 if neuron(X[i], model) >= 0.5 else 0)+(1-y)*(0 if neuron(X[i], model) >= 0.5 else 1))
    return A
```
“Оставить в живых” только P самых приспособленных. И вернуться к пункту 2, повторяя этот цикл несколько раз. Например: сто раз или пока точность не станет 80%.
реализация отбора
```
def selection(offspring, population):
    offspring.sort()
    population = [kid[1] for kid in offspring[:len(population)]]
    return population
```

реализация эволюционного алгоритма

def evolution(population, X_in, Y, number_of_generations, children):
    for i in range(number_of_generations):
        X = [[1]+[v.tolist()] for v in X_in]
        offspring = []
        for genom in population:
            for j in range(children):
                child = mutation(genom)
                child_loss = 1 - accuracy(X_in, Y, child) # or child_loss = binary_crossentropy(X, Y, child)  is better
                offspring.append([child_loss, child])
            population = selection(offspring, population)
    return population

Такую нейроэволюцию можно улучшить. Например, можно ввести дополнительные гены-параметры, как τ — темп мутагенеза и μ — сила мутагенеза. Теперь аддитивные мутации в матрицу весов нейронов будут вносится с вероятность τ, добавляя каждому параметру случайное число в выбранном диапазоне (например от -0.1 до 0.1) умноженное на μ. Эти гены тоже будут подвержены изменчивости.

В идеале, отбор должен контролировать силу и темп мутагенеза на разных этапах эволюции, увеличивая эти параметры до тех пор, пока скачком возможно выбраться из локального максимума ландшафта приспособленности, либо уменьшая их, чтобы медленно и без резких скачков двигаться к глобальному максимуму. Также можно добавить в модель кроссинговер. Теперь потомки будут образовываться путем скрещивания, получив случайным образом по половине генов от двух случайных родителей. В этой схеме тоже необходимо оставить внесение случайных мутаций в геном.

Здесь я считаю уместным привести цитату из книги Александра Маркова и Елены Наймарк:

«Вредные мутации — это движение вниз по склону, полезные — путь наверх. Мутации нейтральные, не влияющие на приспособленность, соответствуют движению вдоль горизонталей — линий одинаковой высоты. Отбраковывая вредные мутации, естественный отбор мешает эволюционирующей последовательности двигаться вниз по ландшафту приспособленности. Поддерживая мутации полезные, отбор пытается загнать последовательность как можно выше.»

Градиентный спуск и метод обратного распространения ошибки

Если следующий материал окажется трудным для понимания, то вернитесь к нему позже. К тому же множество библиотек машинного обучения дают возможность с легкостью реализовать обучение этим методом, не вдаваясь в подробности. Когда мы извлекаем корень, используя калькулятор, нас обычно мало интересует как он это делает, мы прекрасно знаем, что мы хотим получить, а сам счет отдаем машине. Но для тех кому интересен этот метод, мы рассмотрим его вкратце.

Начнем с того, что один выходной нейрон в нашей моделе отвечает только за один класс. Если это объект того класса, за который отвечает нейрон, мы желаем видеть единицу на его выходе, в противном случае — ноль. В реальном же предсказании класса, как мы уже знаем, искусственный нейрон активируется в открытом диапазоне между нулем и единицей, при этом значение может быть сколь угодно близким к этим двум асимптотам. Значит, чем точнее мы угадываем класс, тем меньше абсолютная разница между реальным классом и активацией нейрона, отвечающего за этот класс.

Попробуем создать функцию потери, которая бы возвращала числовое значение штрафа, такое, чтобы оно было маленьким в том случае, когда нейросеть выдает значения близкие к значению класса, и очень большим в том случае, в котором нейросеть выдает значения, приводящие к неправильному определению класса.

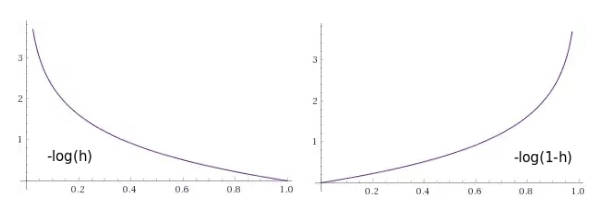Рис. 9 — Графики функции штрафов, как функции от выхода нейрона: 1) в том случае если объект принадлежит этому классу (ожидаем единицу), 2) в том случае если объект не принадлежит этому классу (ожидаем ноль)

Теперь осталось записать функцию потери в виде выражения. Еще раз напомню, что Y для каждого i-го элемента обучающей выборки размером m всегда принимает значения либо ноль, либо один, так что в выражении всегда останется только один из двух членов.

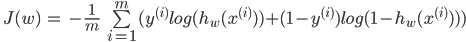
Те, кто знаком с теорией информации, узнают в этом выражении перекрестную энтропию (англ. cross entropy). C точки зрения теории информации, обучением является минимизация перекрестной энтропии между реальным классами и гипотезами модели.

функция потери

def binary_crossentropy(X, Y, model): # loss function
    J = 0
    m = len(Y)
    for i, y in enumerate(Y):
        J += -(1/m)*(y*np.log(neuron(X[i], model))+(1.-y)*np.log(1.-neuron(X[i], model)))
    return J

Проинициализировав коэффициенты матрицы весов случайным образом, мы хотим внести в них изменения, которые сделают нашу модель лучше, или по-другому выражаясь, уменьшат потерю. Если будет известно, насколько влияют веса на функцию потерь, то будет известно, насколько их нужно изменить. Тут нам поможет частная производная — градиент. Именно она показывает, как функция зависит от ее аргументов. На сколько (сверхмалых) величин нужно изменить аргумент, чтобы функция изменилась на одну (сверхмалую) величину. Значит, мы можем переинициализировать матрицу весов следующим образом:

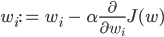
Повторять этот шаг нужно итеративно. По-сути, это и есть постепенный градиентный спуск маленькими шажками, размером с α (этот параметр еще называют темпом обучения), в локальный минимум функционала потери. Другими словами, в каждой точке, задаваемой нынешними значениями W, мы узнаем направление, в котором функционал потери изменяется самым быстрым образом, и динамика обучения напоминает шарик, постепенно скатывающийся в локальный минимум.

градиентный спуск

def gradient_descent(model, X_in, Y, number_of_iteratons=500, learning_rate=0.1):
    X = [[1]+[v.tolist()] for v in X_in]
    m = len(Y)
    for it in range(number_of_iteratons):
        new_model = []
        for j, w in enumerate(model):
            error = 0
            for i, x in enumerate(X):
                error += (1/m) * (neuron(X[i], model) - Y[i]) * X[i][j]
            w_new = w - learning_rate * error
            new_model.append(w_new)
        model = new_model
        model_loss = binary_crossentropy(X, Y, model)
    return model

Метод обратного распространения ошибки продолжает эту цепочку рассуждений на случай многослойной нейронной сети. Благодаря нему можно обучать глубинные слои на основе градиентного спуска. Обучение происходит шаг за шагом от последнего слоя к первому. Думаю, что этой информации вполне хватит, чтобы понять суть этого метода.

Пример обучения нейросети

Предположим, мы хотим узнать вероятность покупки клиента на основе всего одного параметра — его возраста. Мы хотим создать нейрон, который будет возбуждаться в тех случаях, когда вероятность покупки составляет более 50%.

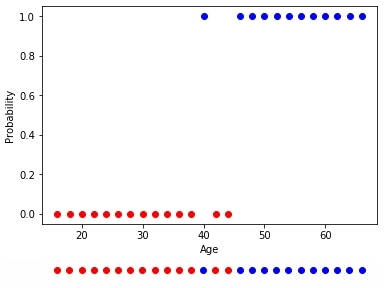Рис. 10 — Обучающая выборка купивших и не купивших

Значит, нейрон имеет один рецептор, связанный с возрастом клиента. Кроме того, мы добавляем один bias член, который будет отвечать за сдвиг. Например, хоть эти множества и линейно неразделимы, но примерная граница, по-другому выражаясь, наилучшая разделяющая гиперповерхность (в одномерном случае — точка), между ними располагается в возрасте 42 лет.

Нейросеть должна давать значения вероятности покупки меньше 0.5 при возрасте до 42 лет, больше 0.5 для более взрослых клиентов. Если вспомнить функцию активации, то она возвращает значения большие 0.5 для положительных аргументов и меньшие 0.5 для — отрицательных. Значит, нужна возможность сдвигать эту функцию активации на какое-то пороговое значение. При этом мы ожидаем такую скорость перелома функции активации, которая бы лучше всего соответствовала обучающей выборке, так как от коэффициентов матрицы весов будет зависеть степень возбуждения каждого нейрона как функция от вектора признаков x, и соответственно вероятность принадлежности элемента с таким вектором признаков к этому классу.

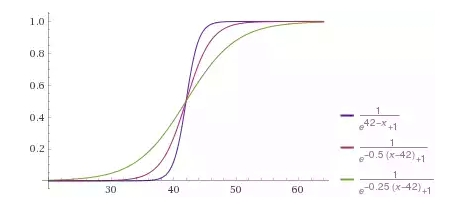Рис. 11 — Ожидаемая реакция нейрона на возраст клиента с разной степенью “уверенности” в результате, регулируемой коэффициентом при аргументе

Теперь запишем это математически и поймем, зачем нам нужен еще один bias-term в матрице весов. Чтобы сместить функцию f(x) вправо, например на 42, мы должны вычесть 42 из ее аргумента f(x-42). При этом мы хотим получить слабый перегиб функции, умножив аргумент, например на 0.25, получив следующую функцию f(0.25(x-24)). Раскрывая скобки, получим:

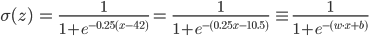
В нашем случае искомый коэффициент матрицы весов w = 0.25, а сдвиг b = -10.5. Но мы можем считать, что b это нулевой коэффициент матрицы весов (w₀=b) в том случае, если для любого примера нулевым признаком всегда будет единица (x₀=1). Тогда, например пятнадцатый «векторизированный» клиент с возрастом в 45 лет, представленный как x⁽¹⁵⁾ = {x⁽¹⁵⁾₀, x⁽¹⁵⁾₁} = [1, 30], мог бы купить с вероятностью 68%. Все эти коэффициенты даже в таком простом примере тяжело прикинуть “на глаз”. Поэтому, собственно, мы и доверяем поиск этих параметров алгоритмам машинного обучения. В нашем примере мы ищем два коэффициента матрицы весов (w₀=b и w₁).

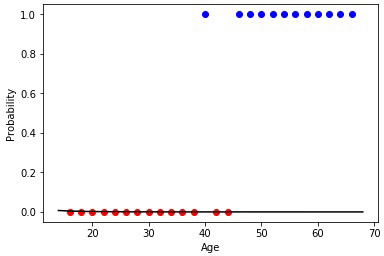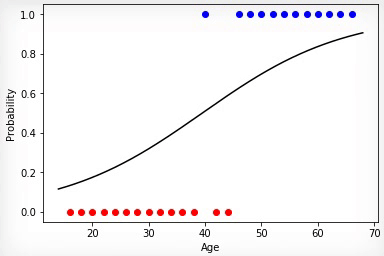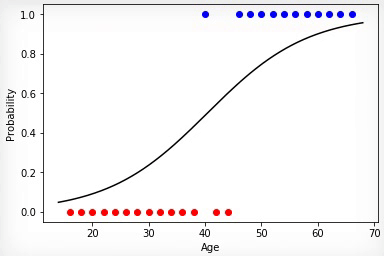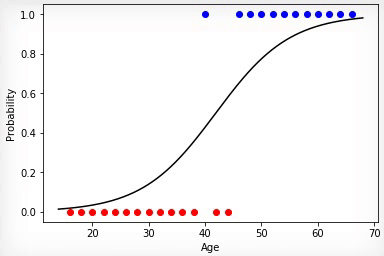Анимация 1 — Эволюционное обучение на данных без нормировки

Проинициализировав коэффициенты матрицы весов случайным образом и использовав эволюционный алгоритм, мы получили обученную нейросеть после смены ста поколений. Чтобы получить нужный результат обучения быстрее и без таких резких скачков, необходимо нормировать данные перед обучением.

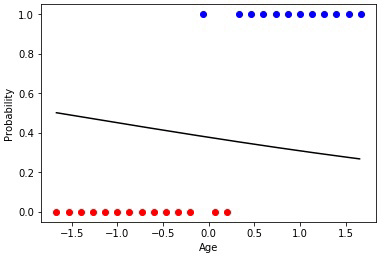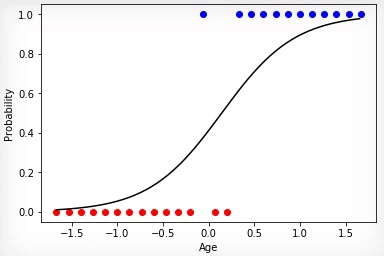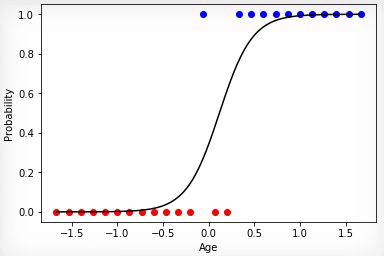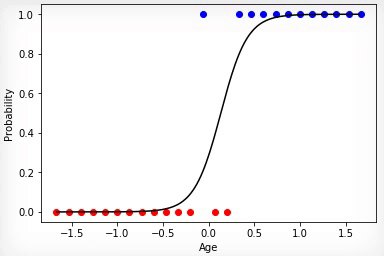Анимация 2 — Эволюционное обучение на нормированных данных

Точнее всего срабатывает метод градиентного спуска. При использовании этого метода данные всегда должны быть нормированы. В отличие от эволюционного алгоритма метод градиентного спуска не испытывает скачков связанных с «мутациями», а постепенно двигается к оптимуму. Но минус в том, что этот алгоритм может застрять в локальном минимуме и уже не выйти из него или градиент может практически «исчезнуть» и обучение прекратится.

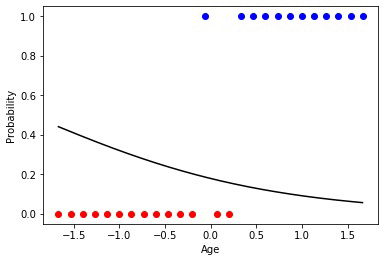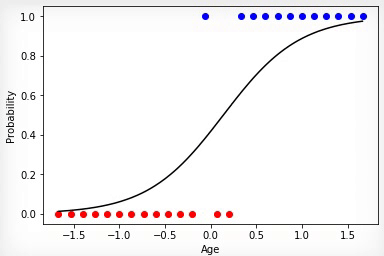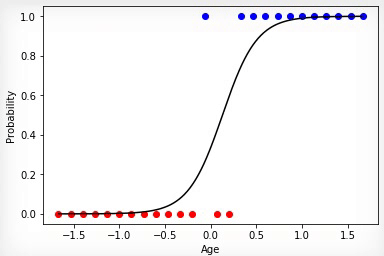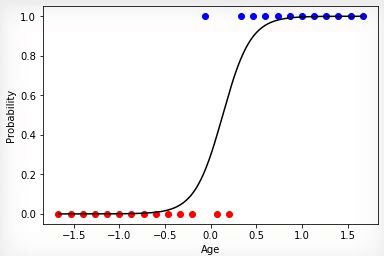Анимация 3 — Обучение на основе метода градиентного спуска

В том случае если множества классов купивших и не купивших линейно разделимы, нейрон будет более “уверен” в своих решениях и изменение степени его активации будет иметь более выраженный перелом на границе этих множеств.

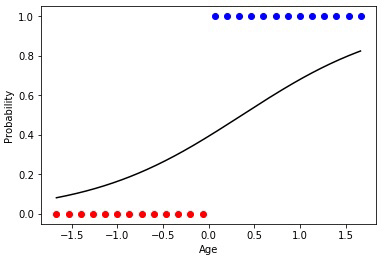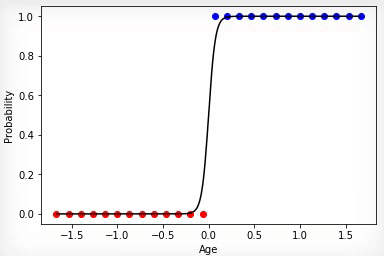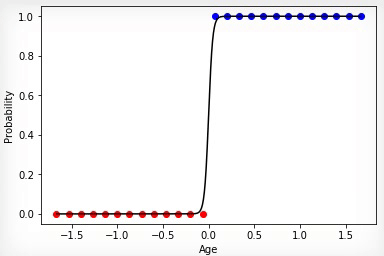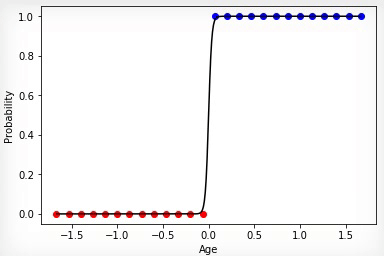Анимация 4 — Обучение на линейно разделимых множествах

На основе рассмотренного можно представить классическую нейросеть в виде вычислительного графа содержащего:

входные вершины x;
вершины, являющиеся нейронами со значениями их выхода a;
вершины, отвечающие за bias b;
ребра, умножающие значения выхода предыдущего слоя на соответствующие им коэффициенты матрицы весов w;
гипотезу h_w,b(x) — результат выхода последнего слоя.

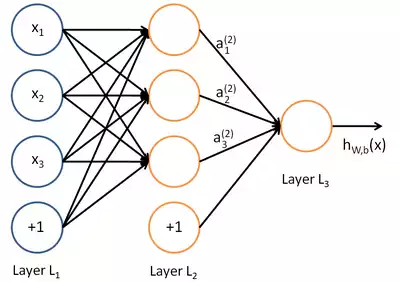Рис. 12 — Вычислительный граф классической искусственной нейросети

Рассмотрим пару примеров онлайн песочницы библиотеки TensorFlow. Во всех примерах необходимо разделить два класса, объекты которых располагаются на плоскости. Входной слой имеет два «рецептора», значения которых соответствуют координатам объекта по осям абсцисс и ординат (плюс один bias, в анимации bias не изображен). Как было сказано, для обучения на линейно разделимых множествах достаточно иметь всего один выходной нейрон, скрытый (ассоциативный) слой отсутствует. Обучение происходит на основе метода обратного распространения ошибки.

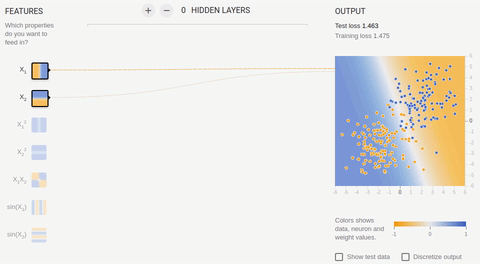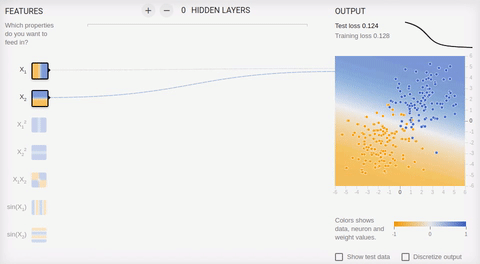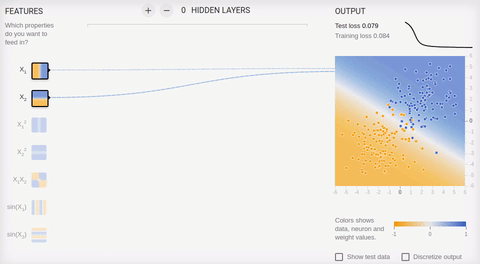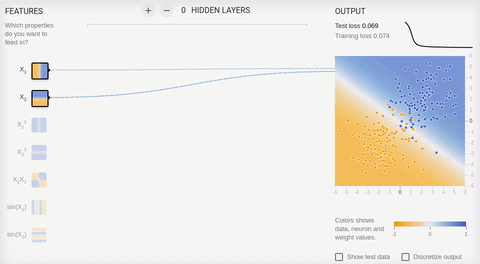Анимация 5 — Один выходной нейрон находит разделяющую прямую

Попробуем усложнить задачу и разделить множества, элементы первого из которых имеют только положительные или только отрицательные значения по обеим координатам, а элементы второго имеют одно положительное и одно отрицательное значение их координат. В этом примере уже не обойтись одной разделяющей прямой, поэтому нам потребуется наличие скрытого слоя. Попробуем начать с самого минимума и добавить два нейрона в скрытый слой.

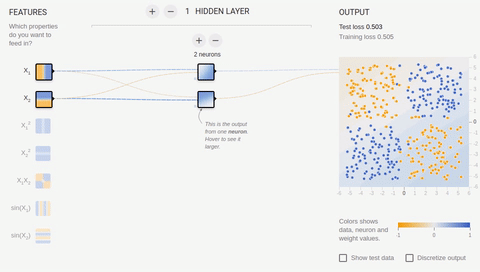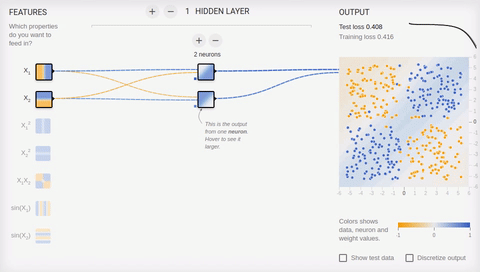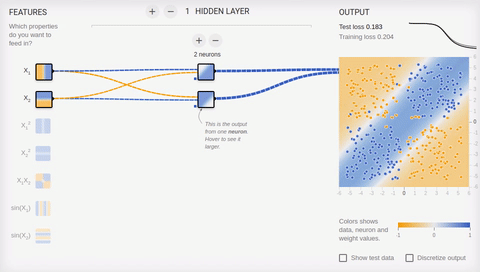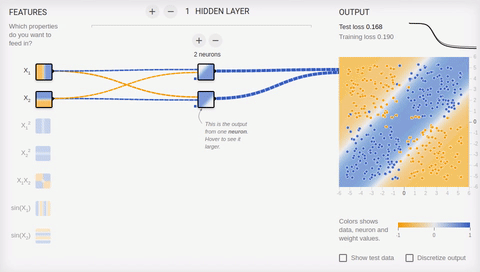Анимация 6 — Два ассоциативных нейрона и две разделяющие прямые

Как мы видим, два нейрона в скрытом слое справляются с этой задачей, хоть и не лучшим образом. Обратите внимание, как в процессе обучения происходит специализация (дифференциация) нейронов. Теперь создадим скрытый слой, состоящий из четырех нейронов.

Анимация 7 — Четыре ассоциативных нейрона и четыре разделяющие прямые

Нейросеть хорошо справилась с этой задачей. Обратите внимание на то, как происходит обучение. Сначала нейросеть нашла самое простое решение — разделяющий коридор. Затем произошла переспециализация нейронов. Теперь каждый скрытый (ассоциативный) нейрон отвечает за свой узкий сегмент.

Попробуем решить достаточно сложную задачу — разделение элементов двух множеств, лежащих в разных спиральных рукавах.

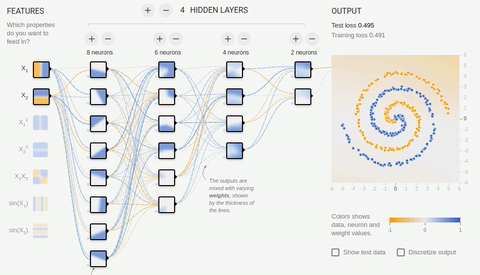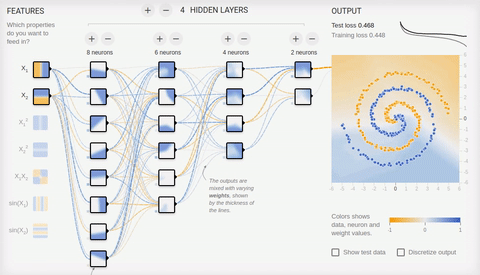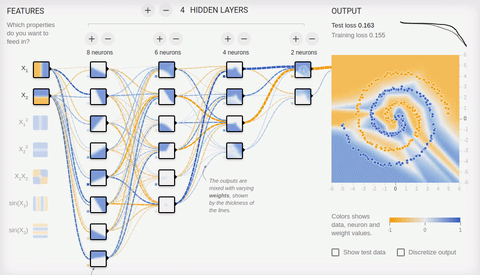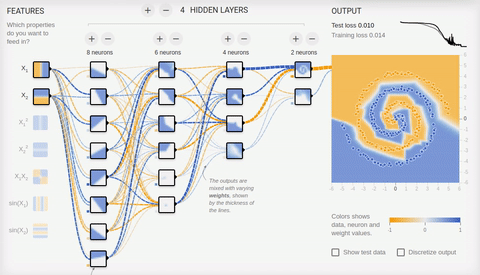Анимация 8 — Многослойная нейросеть с топологией «бутылочное горлышко»

Для решения сложной задачи необходимо множество скрытых слоев. С задачей хорошо справляется нейросеть с топологией «бутылочное горлышко», в которой количество нейронов уменьшается от первого скрытого слоя к последнему. Обратите внимание на то, какие сложные паттерны возникают при специализации ассоциативных нейронов. В случае глубоких нейронных сетей лучше использовать ReLU (rectified linear unit) функцию активации для скрытых нейронов, и обычную логистическую активацию (в идеале softmax-активацию) для последнего слоя.

На этом, я думаю, можно закончить наш сверхкраткий курс искусственных нейронных сетей, и попробовать применить наши знания на практике. Советую построить свою модель на уже готовой библиотеке, которые сейчас есть для любого языка программирования, а также постепенно углублять свои теоретические знания в этом направлении.

Обучение модели

Когда у нас есть и обучающая выборка, и теоретические знания, можем начинать обучение нашей модели. Однако проблема заключается в том, что часто элементы множеств представлены в неравных пропорциях. Купивших может быть 5%, а некупивших — 95%. Как в таком случае производить обучение? Ведь можно добиться 95% достоверности, утверждая, что никто не купит.
Наверное, метрика точности в таком случае должна быть иной, да и обучать нужно тоже разумно, чтобы нейросеть не сделала такого же очевидно неверного вывода. Для этого я предлагаю “кормить” нейросеть обучающими примерами, содержащими равное количество элементов разных классов.

Например, если у нас всего 20,000 примеров и из них 1,000 купивших, можно случайным образом выбрать из каждой группы по 500 примеров и использовать их для обучения. И повторять эту операцию раз за разом. Это немного усложняет реализацию процесса обучения, но зато помогает получить грамотную модель.

Выбрав модель и алгоритм обучения, желательно разделить вашу выборку на части: провести обучение на обучающей выборке, составляющей 70% от всей, и пожертвовать 30% на тестовую выборку, которая потребуется для анализа качества полученной модели.

Оценка качества модели

Подготовив модель, необходимо адекватно оценить ее качество. Для этого введем следующие понятия:

TP (True Positive) — истиноположительный. Классификатор решил, что клиент купит, и он купил.
FP (False Positive) — ложноположительный. Классификатор решил, что клиент купит, но он не купил. Это так называемая ошибка первого рода. Она не так страшна, как ошибка второго рода, особенно в тех случаях, когда классификатор — тест на какое-нибудь заболевание.
FN (False Negative) — ложноотрицательный. Классификатор решил, что клиент не купит, а он мог купить (или уже купил). Это так называемая ошибка второго рода. Обычно при создании модели желательно минимизировать ошибку второго, даже увеличив тем самым ошибку первого рода.
TN (True Negative) — истиноотрицательный. Классификатор решил, что клиент не купит, и он не купил.

Кроме прямой оценки достоверности в процентах существуют такие метрики, как точность (англ. precision) и полнота (англ. recall), основанные на вышеприведенных результатах бинарной классификации.

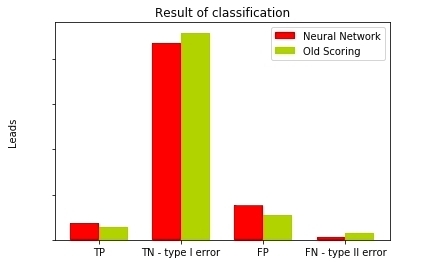Рис. 13 — Сравнение результатов классификации разных моделей

Как мы видим, нейросеть имеет в три раза меньшую ошибку второго рода по сравнению со старой скоринг-моделью, и это очень неплохо. Ведь упуская потенциальных клиентов, мы упускаем потенциальную прибыль. Давайте теперь на основе имеющихся данных выведем метрики качества наших моделей.

Метрика достоверности

Самая простая метрика — это метрика достоверности (англ. Accuracy). Но эта метрика не должна быть единственной метрикой модели, как мы уже поняли. Особенно в тех случаях, когда существует перекос в выборке, то есть представители разных классов встречаются с разной вероятностью.

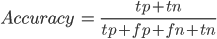
Точность и полнота

Точность (англ. precision) показывает отношение верно угаданных объектов класса ко всем объектам, которые мы определили как объекты класса. Например, мы решили, что купит 115, а из них реально купило 37, значит точность составляет 0.33. Полнота (англ. recall) показывает отношение верно угаданных объектов класса ко всем представителям этого класса. Например, среди нами угаданных реально купило 37, а всего купивших было 43. Значит наша полнота составляет 0.88.

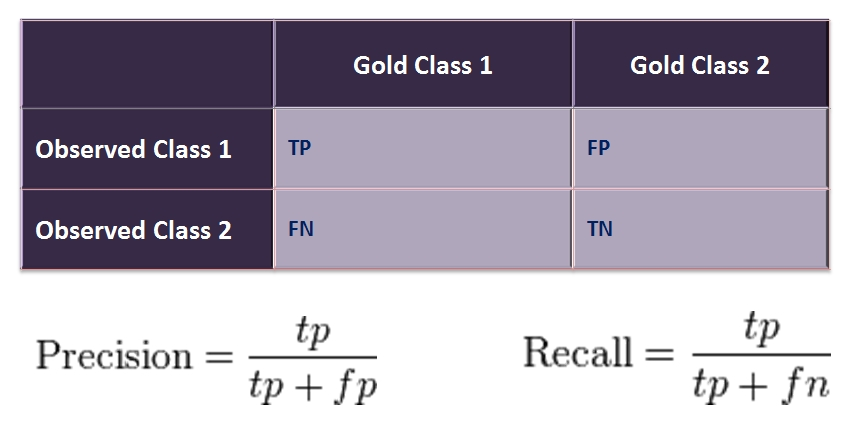Рис. 14 — Таблица ошибок или confusion matrix

F-мера

Также существует F-мера (англ. F1 score) — среднее гармонической точности и полноты. Помогает сравнить модели, используя одну числовую меру.

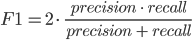
Используя все эти метрики, проведем оценку наших моделей.

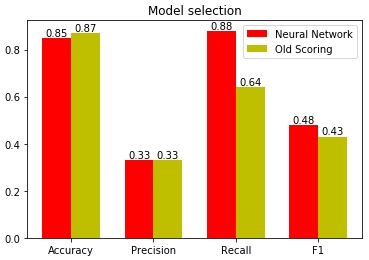Рис. 15 — Оценка качества моделей на основе разных статистических метрик

Как видно на диаграмме, самый большой перекос в качестве моделей именно в метрике полноты (англ. recall). Нейронная сеть угадывает 88% потенциальных клиентов, упуская только 12%. Старая же скоринг модель упускала 36% процентов потенциальных клиентов, пропуская к менеджерам лишь 64%. Вот собственно почему лучше доверить нейросети подбирать коэффициенты значимости разных ответов, влияющих на скоринг. Ведь машина способна удерживать в своей памяти всю выборку, находить в ней закономерности и строить модель, обладающую хорошей предсказательной способностью.

Интерпретация модели

Когда у нас есть готовая модель, мы можем использовать ее, ожидая той точности, которой нам дал анализа ее качества. Если есть возможность внедрить сложную (многослойную) модель в свой процесс, то хорошо, но если нет, то можно получить привычную скоринг модель из однослойной нейросети. Именно для этого мы так подробно ознакомились с устройством нейросетей, чтобы смело заглянуть ей под капот.

Сравним формулу линейной скоринг модели и функцию работы одного нейрона (или однослойной нейросети):

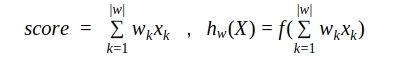
Видим, что выражение, являющееся аргументом функции активации, идентично линейной формуле скоринга. Значит, “вытащив” значения матрицы весов из однослойной нейросети, мы можем воспользоваться ими как коэффициентами скоринг модели. Только теперь эти коэффициенты аккуратно подобраны алгоритмом на основе большого количества данных.

Теперь сравним результаты линейного скоринга на основе коэффициентов до и после внедрения нейросети. Вспомним, что логистическая функция активации дает значение (с точки зрения нейросети — вероятность принадлежности к классу купивших) большее 0.5 при положительном значении аргумента (скоринга на основе матрицы весов). Мы умножили значения нейронного скоринга на сто с целью масштабирования баллов и прибавили пятьсот как пороговое значение. У старого скоринга проходной порог подбирался вручную и составлял сто семьдесят. Все это просто линейные манипуляции, никак не влияющие на саму модель.

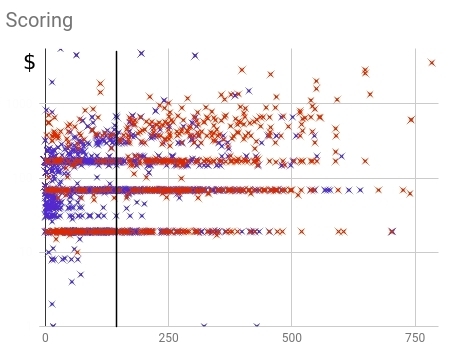Рис. 16 — Распределение купивших (красных) и не купивших (синих) клиентов в рамках старой скоринг модели

Как видно из распределения, клиенты слишком сильно размазаны по всему диапазону значений скоринга. Полнота (доля предсказанных моделью из всего числа купивших клиентов) составляет 64%.

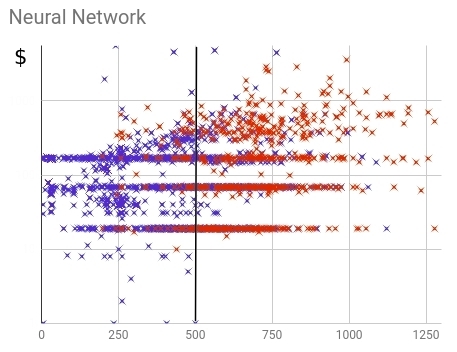Рис. 17 — Распределение купивших (красных) и не купивших (синих) клиентов в рамках нейронной скоринг модели

Из распределения видно, что нейросеть справилась с задачей разделения купивших и не купивших пользователей лучше старой модели. Не купившие, в основной своей массе, получили значения ниже порогового, купившие — выше. Полнота (доля предсказанных моделью из всего числа купивших клиентов) составляет 88%.

Результат

Решая нашу задачу мы хотели уделить как можно больше времени тем, кто купит тариф на большую сумму. Мало того, мы пожелали создать такую скоринг модель, в которой клиенты, покупающие самый дешевый тариф, не набирали бы проходной балл.

На этот раз для обучении нейронной сети мы разделили выборку на класс купивших на определенную сумму и выше, и на класс купивших на меньшую сумму или вообще не купивших.

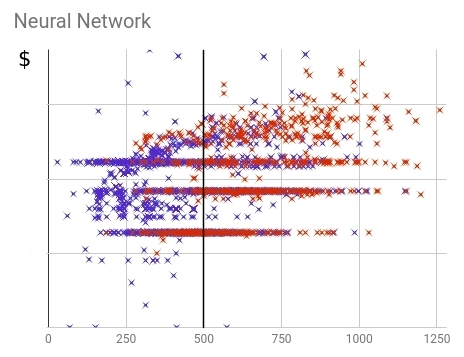Рис. 18 — Распределение купивших (красных) и не купивших (синих) клиентов в рамках финальной нейронной скоринг модели

При прочих, практически равных показателях точности, нейронная сеть смогла добиться большей полноты и смогла охватить 87% купивших дорогие тарифные планы. Для сравнения: старый скоринг справился только с 77%. Значит, в будущем мы сможем покрыть еще 10% весомых и потенциальных клиентов. При этом процент купивших дорогие тарифы из прошедших скоринг практически одинаков: 23% и 24% для нейросети и старой модели соответственно. При этом видно, что значение скоринга хорошо коррелирует с суммой покупки.

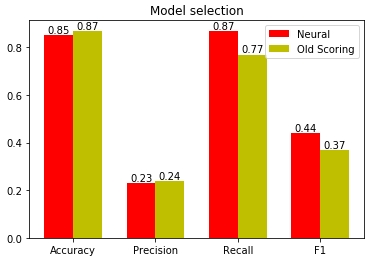Рис. 19 — Сравнение качества старой и новой скоринг модели

Итак, в этой статье мы:

Рассмотрели все основные этапы data-mining.
Узнали много полезных приемов как при подготовке данных, так и при обучении.
Достаточно глубоко познакомились с теорией классических искусственных нейронных сетей.
Рассмотрели разные статистические подходы к анализу качества модели.
Описали все этапы от создания до разбора и внедрения нейронной сети на примере построения линейной скоринг модели.
Показали, как современные алгоритмы машинного обучения могут помочь в решении реальных бизнес-задач.

Если у вас остались вопросы, пожелания или замечания, давайте обсудим в комментариях.