http://habrahabr.ru/post/248159/

Давайте знакомиться, это я.

То есть, модель моей башки, отрендеренная в программе, которую мы сделаем за ближайшие час-два.

В прошлый раз мы нарисовали проволочную сетку трёхмерной модели, в этот раз мы зальём полигоны. Точнее, треугольники, так как OpenGL практически любой полигон триангулирует, поэтому ни к чему разбирать сложный случай. Напоминаю, что этот цикл статей создан для самостоятельного программирования. Время, которое я здесь привожу — это не время чтения моего кода. Это время написания вашего кода с нуля. Мой код здесь только для того, чтобы сравнить ваш (рабочий) код с моим. Я совсем не являюсь хорошим программистом, поэтому ваш код может быть существенно лучше моего. Любая критика приветствуется, любым вопросам рад.

Пожалуйста, если вы следуете этому туториалу и пишете свой код, выкладывайте его на github.com/code.google.com и им подобные и давайте ссылки в комментариях! Это может хорошо помочь как и вам (другие люди могут чего посоветовать), так и будущим читателям.

Рисуем заполненный треугольник.

Итак, тема на сегодня (примерно на два часа для плохо программирующих, но мотивированных студентов): отрисовка двумерных треугольников. В прошлый раз мы разобрали алгоритм Брезенхэма для растеризации отрезка, теперь задача нарисовать заполненный треугольник. Вы будете смеяться, но это нетривиальная задача. Я не знаю почему, но я знаю, что это так. Большинство моих студентов без подсказок проводят над этой задачей существенно больше пары часов. Давайте определимся с методом, а затем будем программировать.

В самом начале давайте рассмотрим вот такой псевдокод:

triangle(vec2 points[3]) {
    vec2 bbox[2] = find_bounding_box(points);
    for (each pixel in the bounding box) {
        if (inside(bbox, pixel)) {
            put_pixel(pixel);
        }
    }
}

Я очень люблю этот метод. Он простой и рабочий. Найти описывающий прямоугольник крайне просто, проверить принадлежность точки двумерному треугольнику (да и любому выпуклому полигону) тоже просто.

Оффтоп: если мне нужно будет написать код, который будет крутиться на, скажем, самолёте, и этот код должен будет проверять принадлежность точки полигону, я никогда не сяду на этот самолёт. Это на удивление сложная проблема, если мы хотим её решить надёжно.

Почему я люблю этот код? Да потому, что, увидев такое, совсем новичок в программировании его воспримет с энтузиазмом, человек, немного знакомый с программированием, только самодовольно хмыкнет, мол, вот идиот писал. А эксперт в программировании компьютерной графики просто пожмёт плечами, мол, ну да, так оно и работает в реальной жизни. Массивно-параллельные вычисления в тысячах маленьких графических процессоров (я говорю про обычные потребительские компьютеры) творят чудеса. Но мы будем писать код под центральный процессор, поэтому этот метод использовать не будем. Да и какая разница, как оно там в кремнии, нашей абстракции вполне хватит для понимания принципа работы.

Окей, начальная заглушка будет выглядеть следующим образом:

void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) {
    line(t0, t1, image, color);
    line(t1, t2, image, color);
    line(t2, t0, image, color);
}

[...]

    Vec2i t0[3] = {Vec2i(10, 70),   Vec2i(50, 160),  Vec2i(70, 80)};
    Vec2i t1[3] = {Vec2i(180, 50),  Vec2i(150, 1),   Vec2i(70, 180)};
    Vec2i t2[3] = {Vec2i(180, 150), Vec2i(120, 160), Vec2i(130, 180)};


    triangle(t0[0], t0[1], t0[2], image, red);
    triangle(t1[0], t1[1], t1[2], image, white);
    triangle(t2[0], t2[1], t2[2], image, green);

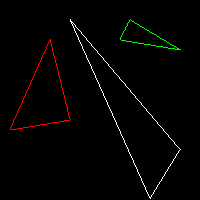
Как обычно, на гитхабе доступен отпечаток кода. В этом коде всё просто: я даю три треугольника для начальной отладки вашего кода; если внутри функции triangle просто сделать вызов line(), то получим контур треугольника. Как нарисовать заполненный треугольник?

Хороший метод отрисовки треугольника должен обладать следующими свойствами:

• Он должен быть (сюрприз) простым и быстрым
• Он должен быть симметричным: картинка не должна зависеть от порядка вершин, переданных в функцию отрисовки
• Если два треугольника имеют две общие вершины, между ними не должно быть дырок из-за округлений растеризации.

Требований можно добавлять гораздо больше, но мы довольствуемся этими тремя.

Традиционно используется line sweeping (заметание отрезком?):

• Сортируем вершины треугольника по их y-координате
• Растеризуем параллельно левую и правую границы треугольника
• Отрисовываем горзонтальный отрезок между левой и правой точкой границы

Тут мои студенты начинают теряться, кто левый, кто правый, да и вообще, в треугольнике три отрезка…
В этот момент я оставляю своих студентов примерно на час, чтение моего кода куда как менее ценно, нежели сравнение своего (выстраданного!) кода с моим.

[прошёл час]

Как рисую я? Ещё раз, если у вас есть лучший метод, то я его с огромным удовольствием возьму на вооружение. Давайте предположим, что у нас есть три точки треугольника, t0,t1,t2, они отсортированы по возрастанию y-координаты.
Тогда граница А будет между t0 и t2, граница Б будет между t0 и t1, а затем между t1 и t2.

void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) {
    // sort the vertices, t0, t1, t2 lower-to-upper (bubblesort yay!)
    if (t0.y>t1.y) std::swap(t0, t1);
    if (t0.y>t2.y) std::swap(t0, t2);
    if (t1.y>t2.y) std::swap(t1, t2);

    line(t0, t1, image, green);
    line(t1, t2, image, green);
    line(t2, t0, image, red);
}

Здесь у нас граница А нарисована красным, а граница Б зелёным.



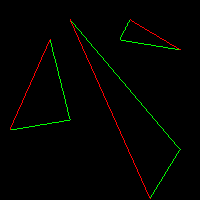
Граница Б, к сожалению, составная. Давайте отрисуем нижнюю половину треугольника, разрезав его по горизонтали в точке излома границы Б.

void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) {
    // sort the vertices, t0, t1, t2 lower-to-upper (bubblesort yay!)
    if (t0.y>t1.y) std::swap(t0, t1);
    if (t0.y>t2.y) std::swap(t0, t2);
    if (t1.y>t2.y) std::swap(t1, t2);

    int total_height = t2.y-t0.y;
    for (int y=t0.y; y<=t1.y; y++) {
        int segment_height = t1.y-t0.y+1;
        float alpha = (float)(y-t0.y)/total_height;
        float beta  = (float)(y-t0.y)/segment_height; // be careful with divisions by zero
        Vec2i A = t0 + (t2-t0)*alpha;
        Vec2i B = t0 + (t1-t0)*beta;
        image.set(A.x, y, red);
        image.set(B.x, y, green);
    }
}

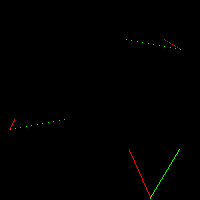
Заметьте, что в этот раз у меня получились разрывные отрезки. В отличие от прошлого раза (где мы рисовали прямые) я не заморочился поворотом изображения на 90°. Почему? Это оказывается не всем очевидным моментом. Просто если мы соединим горизонтальными линиями соответствующие пары точек, то пробелы пропадут:



Теперь осталось отрисовать вторую половину треугольника. Это можно сделать, добавив второй цикл:

void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) {
    // sort the vertices, t0, t1, t2 lower-to-upper (bubblesort yay!)
    if (t0.y>t1.y) std::swap(t0, t1);
    if (t0.y>t2.y) std::swap(t0, t2);
    if (t1.y>t2.y) std::swap(t1, t2);

    int total_height = t2.y-t0.y;
    for (int y=t0.y; y<=t1.y; y++) {
        int segment_height = t1.y-t0.y+1;
        float alpha = (float)(y-t0.y)/total_height;
        float beta  = (float)(y-t0.y)/segment_height; // be careful with divisions by zero
        Vec2i A = t0 + (t2-t0)*alpha;
        Vec2i B = t0 + (t1-t0)*beta;
        if (A.x>B.x) std::swap(A, B);
        for (int j=A.x; j<=B.x; j++) {
            image.set(j, y, color); // attention, due to int casts t0.y+i != A.y
        }
    }
    for (int y=t1.y; y<=t2.y; y++) {
        int segment_height =  t2.y-t1.y+1;
        float alpha = (float)(y-t0.y)/total_height;
        float beta  = (float)(y-t1.y)/segment_height; // be careful with divisions by zero
        Vec2i A = t0 + (t2-t0)*alpha;
        Vec2i B = t1 + (t2-t1)*beta;
        if (A.x>B.x) std::swap(A, B);
        for (int j=A.x; j<=B.x; j++) {
            image.set(j, y, color); // attention, due to int casts t0.y+i != A.y
        }
    }
}

На этом можно было бы успокоиться, но у меня случается несварение, когда я дважды вижу один и тот же код, да ещё так рядом. Поэтому сделаем его чуть менее читаемым, зато более простым для модификаций.

void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) {
    if (t0.y==t1.y && t0.y==t2.y) return; // i dont care about degenerate triangles
    // sort the vertices, t0, t1, t2 lower-to-upper (bubblesort yay!)
    if (t0.y>t1.y) std::swap(t0, t1);
    if (t0.y>t2.y) std::swap(t0, t2);
    if (t1.y>t2.y) std::swap(t1, t2);
    int total_height = t2.y-t0.y;
    for (int i=0; i<total_height; i++) {
        bool second_half = i>t1.y-t0.y || t1.y==t0.y;
        int segment_height = second_half ? t2.y-t1.y : t1.y-t0.y;
        float alpha = (float)i/total_height;
        float beta  = (float)(i-(second_half ? t1.y-t0.y : 0))/segment_height; // be careful: with above conditions no division by zero here
        Vec2i A =               t0 + (t2-t0)*alpha;
        Vec2i B = second_half ? t1 + (t2-t1)*beta : t0 + (t1-t0)*beta;
        if (A.x>B.x) std::swap(A, B);
        for (int j=A.x; j<=B.x; j++) {
            image.set(j, t0.y+i, color); // attention, due to int casts t0.y+i != A.y
        }
    }
}

Отпечаток кода для отрисовки 2d треугольников.

Рисуем модель

Мы умеем уже отрисовывать модель с пустыми треугольниками, давайте их зальём случайным цветом, это поможет нам проверить, насколько хорошо мы закодировали заполнение треугольников. Вот код.

    for (int i=0; i<model->nfaces(); i++) {
        std::vector<int> face = model->face(i);
        Vec2i screen_coords[3];
        for (int j=0; j<3; j++) {
            Vec3f world_coords = model->vert(face[j]);
            screen_coords[j] = Vec2i((world_coords.x+1.)*width/2., (world_coords.y+1.)*height/2.);
        }
        triangle(screen_coords[0], screen_coords[1], screen_coords[2], image, TGAColor(rand()%255, rand()%255, rand()%255, 255));
    }

Всё просто: как и раньше, пробегаем по всем треугольникам, превращаем мировые координаты в экранные и рисуем треугольники. Подробное описание разных систем координат в последущих статьях. Должно получиться нечто вроде этого:

Плоская тонировка.

Давайте теперь убирать эти клоунские цвета и освещать нашу модель.
Капитан Очевидность: «При одной и той же итенсивности света полигон освещён максимально ярко, если свет ему перпендикулярен».
Давайте сравним:



Нулевую освещённость мы получим, если полигон параллелен вектору света.
Перефразируем: интенсивность освещённости равна скалярному произведению вектора света и нормали к данному треугольнику.
Нормаль к треугольнику может быть посчитана просто как векторное произведение двух его рёбер.

    for (int i=0; i<model->nfaces(); i++) {
        std::vector<int> face = model->face(i);
        Vec2i screen_coords[3];
        Vec3f world_coords[3];
        for (int j=0; j<3; j++) {
            Vec3f v = model->vert(face[j]);
            screen_coords[j] = Vec2i((v.x+1.)*width/2., (v.y+1.)*height/2.);
            world_coords[j]  = v;
        }
        Vec3f n = (world_coords[2]-world_coords[0])^(world_coords[1]-world_coords[0]);
        n.normalize();
        float intensity = n*light_dir;
        if (intensity>0) {
            triangle(screen_coords[0], screen_coords[1], screen_coords[2], image, TGAColor(intensity*255, intensity*255, intensity*255, 255));
        }
    }

Но ведь скалярное произведение может быть отрицательным, что это означает? Это означает, что свет падает позади полигона. Если модель хорошая (обычно не наша забота, а 3д моделеров), то мы просто можем этот треугольник не рисовать. Это позволяет быстро убрать часть невидимых треугольников. В англоязычной литературе называется Back-face culling.


Модель моей головы выглядит детальнее? Ну так в ней четверть миллиона треугольников. Ничего, детали мы добавим позже, получив картинку, которую я дал для затравки в первой статье.

Обратите внимание, внутренняя полость рта нарисовалась поверх губ. Ну а что, такое быстрое отсечение невидимых треугольников убирает всё ненужное только для выпуклых моделей. Эти огрехи мы уберём в следующий раз, закодировав z-buffer.
Текущая версия рендерера.