Постановка задачи

Цель этого цикла статей — показать, как работает OpenGL, написав его (сильно упрощённый!) клон самостоятельно. На удивление часто сталкиваюсь с людьми, которые не могут преодолеть первоначальный барьер обучения OpenGL/DirectX. Таким образом, я подготовил краткий цикл из шести лекций, после которого мои студенты выдают неплохие рендеры.

Итак, задача ставится следующим образом: не используя никаких сторонних библиотек (особенно графических) получить примерно такие картинки:

Внимание, это обучающий материал, который в целом повторит структуру библиотеки OpenGL. Это будет софтверный рендер, я не ставлю целью показать, как писать приложения под OpenGL. Я ставлю целью показать, как сам OpenGL устроен. По моему глубокому убеждению, без понимания этого написание эффективных приложений с использованием 3D библиотек невозможно.

Я постараюсь не перевалить за 500 строк в конечном коде. Моим студентам требуется от 10 до 20 часов программирования, чтобы начать выдавать подобные рендеры. На вход получаем текстовый файл с полигональной сеткой + картинки с текстурами, на выход отрендеренную модель. Никакого графического интерфейса, запускаемая программа просто генерирует файл с картинкой.

Поскольку целью является минимизация внешних зависимостей, то я даю своим студентам только один класс, позволяющий работать с TGA файлами. Это один из простейших форматов, поддерживающий картинки в формате RGB/RGBA/чёрно-белые. То есть, в качестве отправной точки мы получаем простой способ работы с картинками. Заметьте, единственная функциональность, доступная в самом начале (помимо загрузки и сохранения изображения), это возможность установить цвет одного пикселя.

Никаких функций отрисовки отрезков-треугольников, это всё придётся писать вручную.

Я даю свой исходный код, который пишу параллельно со студентами, но не рекомендую его использовать, в этом просто нет смысла.

Весь код доступен на гитхабе, здесь находится начальный код, который я даю своим студентам.

#include "tgaimage.h"

const TGAColor white = TGAColor(255, 255, 255, 255);
const TGAColor red   = TGAColor(255, 0,   0,   255);

int main(int argc, char** argv) {
        TGAImage image(100, 100, TGAImage::RGB);
        image.set(52, 41, red);
        image.flip_vertically(); // i want to have the origin at the left bottom corner of the image
        image.write_tga_file("output.tga");
        return 0;
}

output.tga должен выглядеть примерно так:

Алгоритм Брезенхэма

Цель первой лекции — сделать рендер в проволочной сетке, для этого нужно научиться рисовать отрезки.
Можно просто пойти и почитать, что такое алгоритм Брезенхэма, но большинство моих студентов буксуют, читая сразу целочисленную версию, поэтому давайте напишем код сами.

Как выглядит простейший код, рисующий отрезок между двумя точками (x0, y0) и (x1, y1)?
Видимо, как-то так:

void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
    for (float t=0.; t<1.; t+=.01) {
        int x = x0*(1.-t) + x1*t;
        int y = y0*(1.-t) + y1*t;
        image.set(x, y, color);
    }
}

Снапшот кода доступен на гитхабе.

Проблема этого кода (помимо эффективности) это выбор константы, которую я взял равной .01.
Если вдруг мы возьмём её равной .1, то наш отрезок будет выглядеть вот так:

Мы легко можем найти нужный шаг: это просто количество пикселей, которые нужно нарисовать.
Простейший (с ошибками!) код выглядит примерно так:

void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
    for (int x=x0; x<=x1; x++) {
        float t = (x-x0)/(float)(x1-x0);
        int y = y0*(1.-t) + y1*t;
        image.set(x, y, color);
    }
}

Осторожно: наипервейший источник ошибок в подобном коде у моих студентов — это целочисленное деление типа (x-x0)/(x1-x0).

Далее, если мы попробуем этим кодом нарисовать вот такие линии:

line(13, 20, 80, 40, image, white);
line(20, 13, 40, 80, image, red);
line(80, 40, 13, 20, image, red);

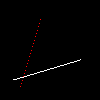
То выяснится, что одна линия хороша, вторая с дырками, а третьей вовсе нет.
Обратите внимание, что первая и вторая строчки (в коде) дают одну и ту же линию разного цвета. Белую мы уже видели, она хорошо отрисовывается. Я надеялся перекрасить белую в красный цвет, не получилось. Это тест на симметричность: результат отрисовки сегмента не должен зависеть от порядка точек: сегмент (a,b) дожен быть ровно таким же, как и сегмент (b,a).

Дырки в одном из сегментов из-за того, что его высота больше ширины.
Мои студенты часто мне предлагают такой фикс: if (dx>dy) {for (int x)} else {for (int y)}.
Ну ёлки!

void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
    bool steep = false;
    if (std::abs(x0-x1)<std::abs(y0-y1)) { // if the line is steep, we transpose the image
        std::swap(x0, y0);
        std::swap(x1, y1);
        steep = true;
    }
    if (x0>x1) { // make it left-to-right
        std::swap(x0, x1);
        std::swap(y0, y1);
    }

    for (int x=x0; x<=x1; x++) {
        float t = (x-x0)/(float)(x1-x0);
        int y = y0*(1.-t) + y1*t;
        if (steep) {
            image.set(y, x, color); // if transposed, de-transpose
        } else {
            image.set(x, y, color);
        }
    }
}

Этот код работает прекрасно. Именно подобной сложности код я хочу видеть в финальной версии нашего рендера.
Разумеется, он неэффективен (множественные деления и тому подобное), но он короткий и читаемый.
Заметьте, в нём нет ассертов, в нём нет проверок на выход за границы, это плохо.
Но я стараюсь не загромождать именно этот код, так как его много читают, при этом я систематически напоминаю про необходимости проверок.

Итак, предыдущий код прекрасно работает, но он может быть оптимизирован.

Оптимизация — опасная вещь, нужно чётко представлять, на какой платформе будет работать код.
Оптимизировать код под графическую карту или просто под центральный процессор — совсем разные вещи.
Перед и во время любой оптимизации код нужно профилировать.
Попробуйте угадать, какая операция здесь наиболее ресурсоёмкая?

Для тестов я рисую 1000000 раз 3 отрезка, которые мы рисовали перед этим. Мой процессор: is Intel® Core(TM) i5-3450 CPU @ 3.10GHz.
Этот код для каждого пикселя вызывает конструктор копирования TGAColor.
А это 1000000 * 3 отрезка * примерно 50 пикслей на отрезок. Немало вызовов.
Где начнём оптимизацию?
Профилировщик нам скажет.

Я откомпилировал код с ключами g++ -ggdb -g3 -pg -O0; затем запустил gprof:

  %   cumulative   self              self     total
 time   seconds   seconds    calls  ms/call  ms/call  name
 69.16      2.95     2.95  3000000     0.00     0.00  line(int, int, int, int, TGAImage&, TGAColor)
 19.46      3.78     0.83 204000000     0.00     0.00  TGAImage::set(int, int, TGAColor)
  8.91      4.16     0.38 207000000     0.00     0.00  TGAColor::TGAColor(TGAColor const&)
  1.64      4.23     0.07        2    35.04    35.04  TGAColor::TGAColor(unsigned char, unsigned char, unsigned char, unsigned char)
  0.94      4.27     0.04                             TGAImage::get(int, int)

10% рабочего времени — это копирование цвета.
Но ещё 70% проводятся в вызове line()! Тут и будем оптимизировать.

Заметим, что каждое деление имеет один и тот же делитель, давайте его вынесем за пределы цикла.
Переменная error даёт нам дистанцию до идеальной прямой от нашего текущего пикселя (x, y).
Каждый раз, как error превышает один пиксель, мы увеличиваем (уменьшаем) y на единицу, и на единицу же уменьшаем ошибку.

Код доступен здесь.

void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
    bool steep = false;
    if (std::abs(x0-x1)<std::abs(y0-y1)) {
        std::swap(x0, y0);
        std::swap(x1, y1);
        steep = true;
    }
    if (x0>x1) {
        std::swap(x0, x1);
        std::swap(y0, y1);
    }
    int dx = x1-x0;
    int dy = y1-y0;
    float derror = std::abs(dy/float(dx));
    float error = 0;
    int y = y0;
    for (int x=x0; x<=x1; x++) {
        if (steep) {
            image.set(y, x, color);
        } else {
            image.set(x, y, color);
        }
        error += derror;

        if (error>.5) {
            y += (y1>y0?1:-1);
            error -= 1.;
        }
    }
}

  %   cumulative   self              self     total
 time   seconds   seconds    calls  ms/call  ms/call  name
 38.79      0.93     0.93  3000000     0.00     0.00  line(int, int, int, int, TGAImage&, TGAColor)
 37.54      1.83     0.90 204000000     0.00     0.00  TGAImage::set(int, int, TGAColor)
 19.60      2.30     0.47 204000000     0.00     0.00  TGAColor::TGAColor(int, int)
  2.09      2.35     0.05        2    25.03    25.03  TGAColor::TGAColor(unsigned char, unsigned char, unsigned char, unsigned char)
  1.25      2.38     0.03                             TGAImage::get(int, int)

А зачем нам нужны плавающие точки? Едиственная причина — это одно деление на dx и сравнение с .5 в теле цикла.
Мы можем избавиться от плавающей точки, заменив переменную error другой, назовём её error2, она равна error*dx*2.
Вот эквивалентный код:

void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
    bool steep = false;
    if (std::abs(x0-x1)<std::abs(y0-y1)) {
        std::swap(x0, y0);
        std::swap(x1, y1);
        steep = true;
    }
    if (x0>x1) {
        std::swap(x0, x1);
        std::swap(y0, y1);
    }
    int dx = x1-x0;
    int dy = y1-y0;
    int derror2 = std::abs(dy)*2;
    int error2 = 0;
    int y = y0;
    for (int x=x0; x<=x1; x++) {
        if (steep) {
            image.set(y, x, color);
        } else {
            image.set(x, y, color);
        }
        error2 += derror2;

        if (error2 > dx) {
            y += (y1>y0?1:-1);
            error2 -= dx*2;
        }
    }
}

  %   cumulative   self              self     total
 time   seconds   seconds    calls  ms/call  ms/call  name
 42.77      0.91     0.91 204000000     0.00     0.00  TGAImage::set(int, int, TGAColor)
 30.08      1.55     0.64  3000000     0.00     0.00  line(int, int, int, int, TGAImage&, TGAColor)
 21.62      2.01     0.46 204000000     0.00     0.00  TGAColor::TGAColor(int, int)
  1.88      2.05     0.04        2    20.02    20.02  TGAColor::TGAColor(unsigned char, unsigned char, unsigned char, unsigned char)

Другой разговор, теперь достаточно убрать ненужные копии при вызове функции, передвая цвет по ссылке (или просто включив флаг компиляции -O3) и всё готово. Ни единого умножения, ни единого деления в коде.
Время работы снизилось с 2.95 секунды до 0.64.

Проволочный рендер.

Теперь всё готово для создания проволочного рендера. Снимок кода и тестовая модель находятся здесь.

Я использовал wavefront obj формат файла для хранения модели. Всё, что нам нужно для рендера, это прочитать из файла массив вершин вида

v 0.608654 -0.568839 -0.416318
[...]
это координаты x,y,z, одна вершина на строку файла

и граней
f 1193/1240/1193 1180/1227/1180 1179/1226/1179
[...]

Тут нас интересуют первое число после каждого пробела, это номер вершины в массиве, который мы прочитали ранее. Таким образом эта строчка говорит, что вершины 1193, 1180 и 1179 образуют треугольник.

Файл model.cpp содержит простейший парсер.

Пишем такой цикл в наш main.cpp и вуаля, наш проволочный рендер готов.

    for (int i=0; i<model->nfaces(); i++) {
        std::vector<int> face = model->face(i);
        for (int j=0; j<3; j++) {
            Vec3f v0 = model->vert(face[j]);
            Vec3f v1 = model->vert(face[(j+1)%3]);
            int x0 = (v0.x+1.)*width/2.;
            int y0 = (v0.y+1.)*height/2.;
            int x1 = (v1.x+1.)*width/2.;
            int y1 = (v1.y+1.)*height/2.;
            line(x0, y0, x1, y1, image, white);
        }
    }

В следующий раз будем рисовать 2D треугольники и подправлять наш рендер.