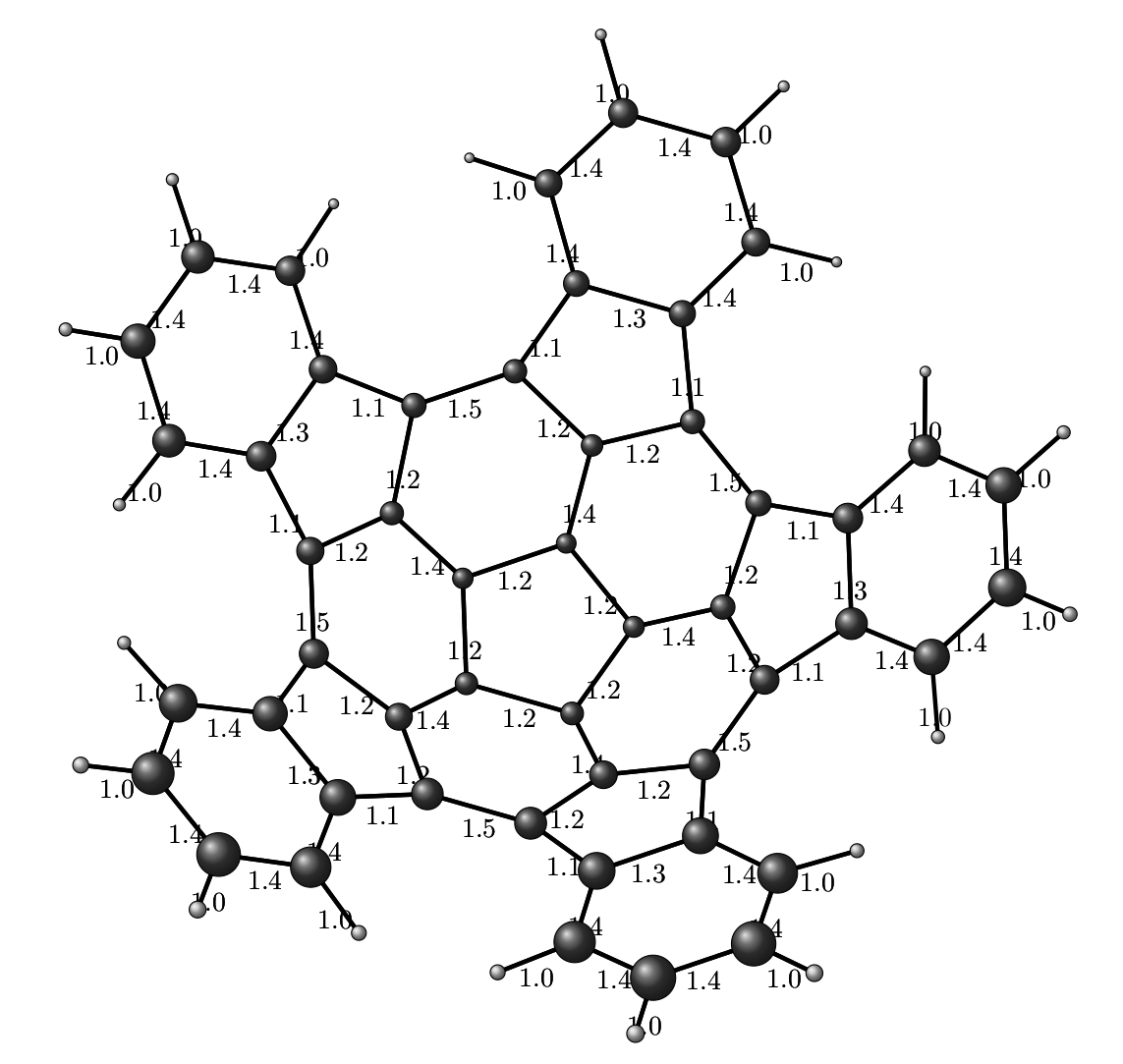
Как нарисовать в TikZ молекулу с порядками связей
- четверг, 13 января 2022 г. в 00:35:16
Иногда перед некоторыми химиками может встать задача получить картинку с публикационным качеством, на которой будет молекула, и над каждой связью будет подписан её порядок. В этом посте, на примере кораннулена, мы познакомимся с простейшими (полуэмпирическими) квантово-химическими расчётами, визуализацией молекул, узнаем про порядки связей, и напишем питоновский скрипт, который будет генерировать из результатов наших расчётов картинку при помощи LaTeX-овского пакета TikZ картинку, которую уже почти-почти можно вставлять в статью. Всё это под катом :)
Вроде мы себе со школы представляем, что есть молекулы, в них могут быть одинарные, двойные, тройные связи, всё такое. Но на самом деле, все эти концепции верны только когда в образовании химической связи участвуют только два атома. В случае же более сложных химических связей (сопряжённые, трёхцентровые, и прочие извращённые), все эти понятия очень сильно размазываются.
Но всё равно, существуют способы каждую химическую связь охарактеризовать, приписав ей порядок связи. Грубо говоря, порядок связи между двумя атомами -- это число пар электронов, которые держат эту пару атомов вместе. Электроны описываются квантовой механикой, и в приниципе, решить задачу о квантовом состоянии электронов (в низшем по энергии состоянии) для любой сейчас не вызывает никаких сложностей. Зная же состояние всех электронов в молекуле (или электронную волновую функцию), мы можем применить её для расчёта порядка связи между каждой парой атомов (даже между несвязанными).
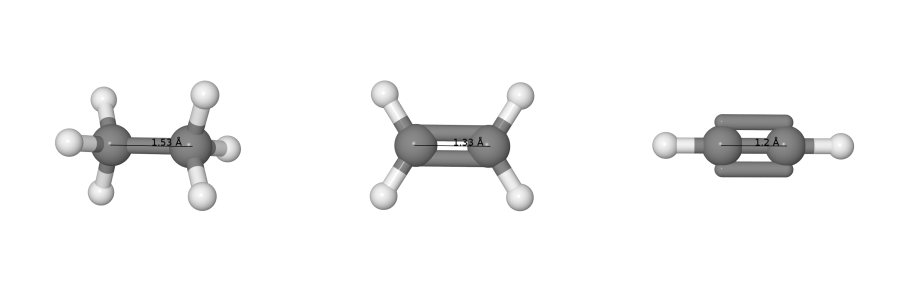
Если мы посчитаем все эти порядки связей, мы наверное захотим их визуализировать. И если с целыми порядками связей всё понятно (одинарная -- одна палочка между атомами, двойная -- две, тройная -- три, см. рисунок выше), то что делать в случае, если порядок связи равен 1.3, уже не так очевидно. Поэтому самым простым решением было бы изобразить все связи в молекулах черточками, а порядок связи подписать сверху.
Но каким бы очевидным это всё ни было для нас, мало какой визуализатор молекул с такой задачей справится. Из тех, что я знаю, это только GaussView, который, за несколько тысяч у.е. своей стоимости, сможет построить абсолютно некрасивую и непубликабельную картинку, так что этот вариант мы отклоняем. Вместо этого, мы попробуем сами сгенерировать картинку в читаемом варианте при помощи LaTeX-овского безумно мощного пакета TikZ.
Чтобы что-то построить, нам надо выбрать молекулу, и что-то с ней сделать. Более интересными вариантами должны быть достаточно большие молекулы (чтобы имело смысл вообще заморачиваться со скриптами) и с достаточно извратными связями, например сопряжённые системы.

От этого всего, у меня в голове от этого всплыл класс молекул, называемых полициклические ароматические углеводороды (ПАУ). Что же означает это название?
"Полициклические" -- значит они содержат в своей структуре несколько циклов, например, циклогексана, циклогексена, или бензола.
"Ароматические" означает, что хотя бы один из циклов должен быть сопряжённым так успешно, что образовалась бы ароматическая система, такая как в бензоле. Что такое ароматичность объяснить в двух словах очень сложно (несмотря на попытки школьного курса это сделать), и откровенно говоря, это определение ароматичности -- это один из священных граалей современной химии. Почитать об этом поподробнее можно, например, в этой статье.
"Углеводороды" же -- это самое простое. Это значит, что молекулы этого класса состоят из двух типов атомов: углерод (C) и водород (H).
Этот класс соединений очень важен как на Земле (ибо является одним из наиболее стрёмных загрязнителей воды и воздуха), так и под землёй (как один из заметных компонентов нефти), и даже давным-давно в одной далёкой-предалёкой галактике в космическом пространстве, где молекулы этого класса, по последним оценкам, ответственны за 10% всего запаса галактического углерода.

В качестве нашей пробной молекулы, выберем кораннулен (C20H10). Это очень красивая молекула, которая представляет собой пять бензольных колец, присоединённых, как лепестки цветка, к пятичленному циклу. Из-за стерического напряжения, эта молекула плоская, и напоминает чашечку. И в эту чашечку даже наливали воду (в количестве одной молекулы, см. картинку выше, выкусите, гомеопаты!).
Чтобы нам визуализировать молекулу, а после чего посчитать её электронную структуру, нам нужны координаты каждого атома. Для этого мы можем воспользоваться или программами-построителями молекулярных геометрий (например, Кемкрафтом, или Jmol-ом), или просто найти эти координаты в интернете. Неплохо можно разжиться на сайте NIST Chemistry Webbook. Почти для каждой молекулы в базе данных, там есть ссылка на скачивание "computed 3d SD file". Тыкая туда, мы скачаем файл в формате SDF. Файл по поиску "corannulene" дан тут:
его скачали с NIST Chemistry Webbook
NIST 08021410203D 1 1.00000 -768.14928
Copyright by the U.S. Sec. Commerce on behalf of U.S.A. All rights reserved.
30 35 0 0 0 0 0 0 0 0999 V2000
2.3479 2.7598 -0.4735 C 0 0 0 0 0 0 0 0 0 0 0 0
2.3108 4.1732 -0.5616 C 0 0 0 0 0 0 0 0 0 0 0 0
3.6394 4.6362 -0.7268 C 0 0 0 0 0 0 0 0 0 0 0 0
4.4974 3.5091 -0.7410 C 0 0 0 0 0 0 0 0 0 0 0 0
3.6992 2.3494 -0.5843 C 0 0 0 0 0 0 0 0 0 0 0 0
1.3863 2.0195 0.1935 C 0 0 0 0 0 0 0 0 0 0 0 0
1.3101 4.9394 0.0122 C 0 0 0 0 0 0 0 0 0 0 0 0
4.1781 1.1717 -0.0353 C 0 0 0 0 0 0 0 0 0 0 0 0
5.8271 3.5678 -0.3589 C 0 0 0 0 0 0 0 0 0 0 0 0
4.0547 5.8962 -0.3297 C 0 0 0 0 0 0 0 0 0 0 0 0
0.2292 2.7852 0.6078 C 0 0 0 0 0 0 0 0 0 0 0 0
0.1931 4.1718 0.5217 C 0 0 0 0 0 0 0 0 0 0 0 0
1.6744 6.3236 0.2317 C 0 0 0 0 0 0 0 0 0 0 0 0
2.9776 6.7779 0.0694 C 0 0 0 0 0 0 0 0 0 0 0 0
5.4848 6.0167 -0.1373 C 0 0 0 0 0 0 0 0 0 0 0 0
6.3264 4.9110 -0.1513 C 0 0 0 0 0 0 0 0 0 0 0 0
1.8210 0.6936 0.5807 C 0 0 0 0 0 0 0 0 0 0 0 0
3.1467 0.2910 0.4720 C 0 0 0 0 0 0 0 0 0 0 0 0
5.6119 1.1509 0.1665 C 0 0 0 0 0 0 0 0 0 0 0 0
6.3949 2.2886 0.0128 C 0 0 0 0 0 0 0 0 0 0 0 0
-0.6061 2.2758 1.0834 H 0 0 0 0 0 0 0 0 0 0 0 0
-0.6692 4.6919 0.9333 H 0 0 0 0 0 0 0 0 0 0 0 0
0.9312 7.0163 0.6204 H 0 0 0 0 0 0 0 0 0 0 0 0
3.2019 7.8080 0.3376 H 0 0 0 0 0 0 0 0 0 0 0 0
5.9103 6.9859 0.1137 H 0 0 0 0 0 0 0 0 0 0 0 0
7.3769 5.0594 0.0892 H 0 0 0 0 0 0 0 0 0 0 0 0
1.1133 0.0161 1.0532 H 0 0 0 0 0 0 0 0 0 0 0 0
3.4230 -0.6854 0.8639 H 0 0 0 0 0 0 0 0 0 0 0 0
6.0864 0.2438 0.5345 H 0 0 0 0 0 0 0 0 0 0 0 0
7.4508 2.2264 0.2670 H 0 0 0 0 0 0 0 0 0 0 0 0
2 1 1 0
1 5 1 0
5 4 1 0
4 3 1 0
2 3 1 0
2 7 2 0
7 12 1 0
12 11 2 0
11 6 1 0
1 6 2 0
4 9 2 0
9 16 1 0
16 15 2 0
15 10 1 0
3 10 2 0
5 8 2 0
8 19 1 0
19 20 2 0
9 20 1 0
6 17 1 0
17 18 2 0
8 18 1 0
10 14 1 0
14 13 2 0
7 13 1 0
11 21 1 0
12 22 1 0
13 23 1 0
14 24 1 0
15 25 1 0
16 26 1 0
17 27 1 0
18 28 1 0
19 29 1 0
20 30 1 0
M END
> <COPYRIGHT>
Collection (C) 2016 copyright by the U.S. Secretary of Commerce on behalf of the United States of America. All rights reserved.
> <DATE>
2014-08-02
> <CAS.NUMBER>
5821-51-2
> <METHOD>
B3LYP/6-31G*
> <DIPOLE.MOMENT>
1.7256 debye
> <ELECTRONIC.ENERGY>
-768.149281981 hartree
> <IR.FREQUENCIES>
"Frequency (cm-1)" "Intensity (km/mol)"
140.9463 4.3688
142.1225 0.0234
142.4048 0.0012
282.0224 0.0000
282.2456 0.0000
311.8107 0.2249
312.3830 0.2255
409.5691 2.3881
409.7950 2.3915
438.7769 0.0000
438.8373 0.0000
452.9639 3.4550
453.1293 3.4725
542.0487 0.0001
547.5829 0.0002
547.6385 0.0000
559.9977 13.1405
605.0577 0.8047
612.4161 0.0001
612.5322 0.0000
648.1763 0.0001
648.4241 0.0001
649.6040 0.0000
673.0974 16.0743
673.1653 16.0396
759.3405 3.7537
759.4716 3.7365
772.4206 0.0000
772.7373 0.0000
812.4235 0.0001
812.6339 0.0000
833.7793 3.4835
833.8699 3.4724
856.2070 111.8882
869.7445 0.0162
869.8674 0.0150
937.3935 0.0000
953.5278 0.0002
960.1158 0.4483
960.1906 0.4495
968.6705 0.0001
968.8939 0.0004
1051.9088 1.2196
1091.4120 0.0000
1091.5541 0.0000
1171.6836 2.1672
1171.8624 3.5197
1171.9526 1.3649
1172.0671 1.7608
1197.1583 0.0000
1197.5385 0.0000
1224.1857 0.0001
1224.4120 0.0001
1244.7627 0.0000
1269.6389 1.0906
1342.9936 9.2123
1343.2742 9.1932
1391.6399 0.0001
1391.8987 0.0000
1440.8503 0.0001
1440.8972 0.0000
1458.5640 1.8664
1458.7683 1.8785
1480.2637 1.8568
1486.1287 2.7000
1486.1836 2.7010
1497.5004 0.0001
1497.7884 0.0001
1527.1617 0.0000
1668.3089 0.0041
1668.4748 0.0110
1669.7603 1.0670
1669.9892 1.0731
1671.5673 0.0030
3174.2046 0.3130
3174.9229 5.3562
3175.0279 5.6321
3175.6846 0.3267
3175.8603 0.0159
3191.4230 1.7604
3191.6544 0.1704
3192.6984 100.6297
3192.7960 102.6391
3194.2245 6.6723
> <ROTATIONAL.CONSTANTS>
0.50785 GHz
0.50779 GHz
0.26288 GHz
> <SOFTWARE>
Gaussian 09, Revision D.01
> <CONTRIBUTOR>
Ethan Ho
$$$$Там находятся координаты всех атомов молекулы, данные в ангстремах (1 Å = 10-10 м). Этот файл мы можем легко визуализировать любым молекулярным вьюером (хороший список есть в Википедии). Я это люблю делать в Jmol, упомянутом выше. Команда jmol 5821-51-2-3d.sdf & позволяет мне узреть сию красоту:
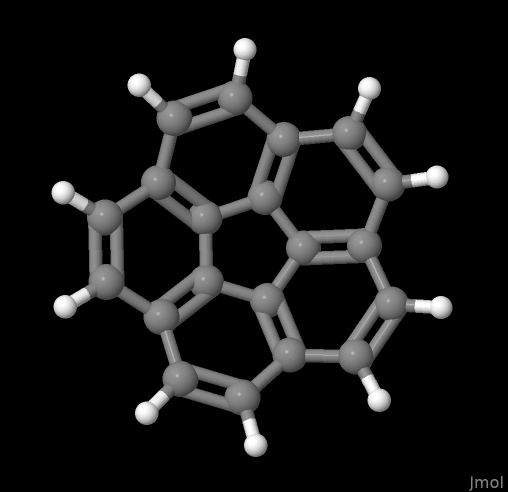
Всю эту молекулку можно теперь сохранять, покрутить и т.д. и т.п., сохранив в нужной конфигурации, используя кнопочкуmodel kit. Заметим, что тут у нас изображены порядки связей (одинарные и двойные черточки), что является результатом того, что они были в нашем изначальном SDF-файле.
После визуализации, выберем удобную для нас ориентацию, т.к. мы будем проецировать молекулу на плоскость xy (что мы и видим в Jmol). После чего вытащим руками геометрию молекулы в XYZ формате, и сохраним её в файл ini.xyz:
30
C 1.69979 2.78101 -1.65228
C 1.35394 3.94963 -2.37448
C 2.55242 4.62236 -2.71788
C 3.63875 3.86951 -2.20816
C 3.11178 2.73154 -1.54944
C 0.85441 2.18448 -0.73191
C 0.14026 4.59911 -2.22325
C 3.77155 2.08239 -0.51937
C 4.86014 4.43362 -1.88024
C 2.61606 5.98885 -2.93335
C -0.48972 2.72307 -0.72415
C -0.82877 3.86975 -1.43236
C 0.14917 5.98162 -2.65393
C 1.32473 6.64151 -2.99106
C 3.94461 6.54944 -2.80136
C 5.01022 5.81082 -2.30138
C 1.52592 1.32553 0.22109
C 2.91115 1.27701 0.32197
C 5.13459 2.52641 -0.31466
C 5.65151 3.64279 -0.96086
H -1.24117 2.27461 -0.07791
H -1.83214 4.27256 -1.31201
H -0.77553 6.55407 -2.63124
H 1.27275 7.70397 -3.21872
H 4.10291 7.60441 -3.01443
H 5.95982 6.31750 -2.14339
H 0.93627 0.76426 0.94247
H 3.34968 0.67971 1.11834
H 5.75177 2.02999 0.43104
H 6.65244 3.97556 -0.69475 Этот файл мы всё также можем открывать Jmol-ом, или другим просмотрщиком молекул, но он нам понадобится для квантово-химических расчётов, т.е. для нахождения наиболее выгодной конфигурации электронов и их энергии.
Итак, мы создали XYZ-файл ini.xyz, содержащий изначальные координаты молекулы. Теперь нам бы эту молекулу оптимизировать (т.е. найти оптимальное расположение всех атомов относительно друг друга, которое будет минимизировать энергию электронов, т.е. всех химических связей). Для этого мы можем воспользоваться программой XTB. Это не полновесная квантовая химия, а т.н. полуэмпирика, т.е. квантово-механический расчёт там происходит, но некоторые вещи хитренько запараметризованы. Подобные методы нужны в первую очередь для ускорения вычислений, что позволяет вычислять параметры гиганских систем в тысячи атомов.
После установки (по-сути прописывания пути к бинарнику) провести расчёт в XTB проще пареной репы:
Запускаем команду xtb ini.xyz --ohess > output.log
Ждём
Получаем результат
Заклинание "ohess" означет "optimization + hessian". Первое -- это реально оптимизация энергии системы как функции координат атомов, а второе -- это расчёт колебательных частот молекулы. Да, молекула колеблется, и чтобы узнать как это она делает, мы можем посчитать вторые производные (Гессиан) её энергии в точке минимума и в таком эффективном потенциале найти формы и частоты колебаний атомов. Полезная штука, которой мы не воспользуемся (но желающие могут их посмотреть в том же Jmol-е, открыв полученный файл g98.out).
Из кучи всяких файлов нас интересуют несколько. xtbopt.xyz -- это там, где содержится оптимизированная геометрия молекулы, минимум на электронной поверхности потенциальной энергии. Этот файл мы переименуем в mol.xyz (вот он под спойлером).
30
energy: -47.909984727343 gnorm: 0.000561323830 xtb: 6.4.1 (afa7bdf)
C 1.70342497008918 2.77120382029981 -1.67459989574751
C 1.35888198845737 3.93605651904526 -2.39411238929612
C 2.55320713127695 4.60662002508876 -2.73648638740711
C 3.63588083564752 3.85619478604766 -2.22858426799746
C 3.11068612200065 2.72184425174820 -1.57229992069963
C 0.86531732896573 2.19467015713543 -0.73988026274033
C 0.15592822786286 4.59298913710542 -2.22131034952792
C 3.76274802514278 2.09303373963485 -0.52926100615237
C 4.84408005491831 4.42856531897689 -1.88049627334238
C 2.61494436161795 5.97362661868611 -2.92622049178063
C -0.46023666409747 2.73788915472265 -0.72902661742635
C -0.79568990271412 3.87198196823774 -1.42956257287266
C 0.17248681723255 5.96311018441904 -2.63939045084267
C 1.33528769236052 6.61597608493287 -2.97271643766150
C 3.92951616360376 6.52499048543271 -2.78412401179422
C 4.98361507251879 5.79437063530864 -2.28963603342726
C 1.53562915869062 1.35451068920168 0.20727845907322
C 2.90574505520454 1.30644138413572 0.30686703629669
C 5.10743028420101 2.54260766563073 -0.32428692794655
C 5.61876291181198 3.64701225551270 -0.96325052396703
H -1.19874170458545 2.29409153379029 -0.07494466776196
H -1.78764656957806 4.28504174115813 -1.30476343298049
H -0.74868879805596 6.52904857077271 -2.60304052043814
H 1.29265341328483 7.67518070709473 -3.18821270199824
H 4.07652658282649 7.57755348473410 -2.98578625864465
H 5.92703793057654 6.29492483888218 -2.11767956737328
H 0.94303089560637 0.80961584278484 0.92983205611095
H 3.34832686183346 0.72523869909287 1.10467238401189
H 5.71098816523577 2.05170297389314 0.42731147860243
H 6.60865448964361 3.99053882857075 -0.69441367658131То, куда мы редиректнули всю выдачу (output.log) -- это собственно лог программы, там много всякой полезной и бесполезной (нам) инфы. Например, там есть энергии орбиталей, частоты колебаний, термодинамические параметры молекулы и т.д. Но что мы хотим -- это порядки связей, вытащенные из электронной плотности. XTB вычисляет т.н. порядки связей Уибера (Wiber bond orders, WBO), которые были введены в работе 1966-го года. Ищем в логе последний кусок такого вида:
Wiberg/Mayer (AO) data.
largest (>0.10) Wiberg bond orders for each atom
---------------------------------------------------------------------------
# Z sym total # sym WBO # sym WBO # sym WBO
---------------------------------------------------------------------------
1 6 C 3.984 -- 6 C 1.345 2 C 1.192 5 C 1.192
2 6 C 3.984 -- 7 C 1.345 3 C 1.192 1 C 1.192
3 6 C 3.984 -- 10 C 1.345 2 C 1.192 4 C 1.192
4 6 C 3.984 -- 9 C 1.345 5 C 1.192 3 C 1.192
5 6 C 3.984 -- 8 C 1.345 4 C 1.192 1 C 1.192
6 6 C 3.986 -- 1 C 1.345 17 C 1.220 11 C 1.220
7 6 C 3.986 -- 2 C 1.345 13 C 1.220 12 C 1.220
8 6 C 3.986 -- 5 C 1.345 19 C 1.220 18 C 1.220
9 6 C 3.986 -- 4 C 1.345 20 C 1.220 16 C 1.220
10 6 C 3.986 -- 3 C 1.345 14 C 1.220 15 C 1.220
11 6 C 3.980 -- 12 C 1.624 6 C 1.220 21 H 0.969
12 6 C 3.980 -- 11 C 1.624 7 C 1.220 22 H 0.969
13 6 C 3.980 -- 14 C 1.623 7 C 1.220 23 H 0.969
14 6 C 3.980 -- 13 C 1.623 10 C 1.220 24 H 0.969
15 6 C 3.980 -- 16 C 1.624 10 C 1.220 25 H 0.969
16 6 C 3.980 -- 15 C 1.624 9 C 1.220 26 H 0.969
17 6 C 3.980 -- 18 C 1.624 6 C 1.220 27 H 0.969
18 6 C 3.980 -- 17 C 1.624 8 C 1.220 28 H 0.969
19 6 C 3.980 -- 20 C 1.623 8 C 1.220 29 H 0.969
20 6 C 3.980 -- 19 C 1.623 9 C 1.220 30 H 0.969
21 1 H 0.998 -- 11 C 0.969
22 1 H 0.998 -- 12 C 0.969
23 1 H 0.998 -- 13 C 0.969
24 1 H 0.998 -- 14 C 0.969
25 1 H 0.998 -- 15 C 0.969
26 1 H 0.998 -- 16 C 0.969
27 1 H 0.998 -- 17 C 0.969
28 1 H 0.998 -- 18 C 0.969
29 1 H 0.998 -- 19 C 0.969
30 1 H 0.998 -- 20 C 0.969
---------------------------------------------------------------------------Собственно, столбцы WBO нам и нужны! Вырезаем их вместе с парами атомов (столбцы #) в отдельный файл "bonds.dat" в формате "<номер первого атома> <номер второго атома> <WBO этой пары атомов>":
1 6 1.345
2 7 1.345
3 10 1.345
4 9 1.345
5 8 1.345
6 1 1.345
7 2 1.345
8 5 1.345
9 4 1.345
10 3 1.345
11 12 1.624
12 11 1.624
13 14 1.624
14 13 1.624
15 16 1.624
16 15 1.624
17 18 1.624
18 17 1.624
19 20 1.624
20 19 1.624
21 11 0.969
22 12 0.969
23 13 0.969
24 14 0.969
25 15 0.969
26 16 0.969
27 17 0.969
28 18 0.969
29 19 0.969
30 20 0.969
1 5 1.192
2 3 1.192
3 4 1.192
4 3 1.192
5 1 1.192
6 17 1.220
7 12 1.220
8 18 1.220
9 16 1.220
10 15 1.220
11 6 1.220
12 7 1.220
13 7 1.220
14 10 1.220
15 10 1.220
16 9 1.220
17 6 1.220
18 8 1.220
19 8 1.220
20 9 1.220
1 2 1.192
2 1 1.192
3 2 1.192
4 5 1.192
5 4 1.192
6 11 1.220
7 13 1.220
8 19 1.220
9 20 1.220
10 14 1.220
11 21 0.969
12 22 0.969
13 23 0.969
14 24 0.969
15 25 0.969
16 26 0.969
17 27 0.969
18 28 0.969
19 29 0.969
20 30 0.969
И после всей этой подготовке можно приступать к построению картинки.
Собственно, имея файлы "mol.xyz" и "bonds.dat", мы запускаем скрипт make_tikz_picture_bond_orders.py из-под спойлера, и получаем наш код.
#! /usr/bin/python
import numpy as np
# сначала прочитаем файл с молекулярной геометрией
inpf = open("mol.xyz", "r") # открываем файл 'mol.xyz' в "read" режиме
count=0 # это просто счётчик строк
xyz = [] # здесь мы будем хранить x,y,z, координаты атомов
atn = [] # а здесь тип атома
for line in inpf: # идём по каждой строке файла
count+=1 # не забывая повышать счётчик
# первые 2 строки xyz-файла -- это число атомов и строка с описанием,
# их мы пропускам, т.к. координаты начинаются с 3й строки
if count>2:
words = line.split() # делим строку на слова
if len(words)>=4: # не обязательно, но вдруг что-то не так с файлом
# первое слово в строке -- тип атома,
# переводим его заодно в строчечные буквы, чтобы
# избежать разночтений
atn.append(words[0].lower())
# ну а потом остальные слова (координаты в ангстремах)
# сохраняем в лист, переводя их floats
xyz.append([float(word) for word in words[1:4]])
inpf.close() # ну и закрываем файл
# теперь читаем файл со связями и их порядками
inpf = open("bonds.dat", "r") # открываем файл 'bonds.dat' в "read" режиме
BondInd = [] # здесь мы будем хранить индексы атомов, между которыми есть связь
BondOrd = [] # а здесь численное значение для связи (предположительно, порядок связи)
for line in inpf: # идём по каждой строке файла
words = line.split() # делим строку на слова
if len(words)>=3: # не обязательно, но вдруг что-то не так с файлом
# индексы переводим в numpy.array, конвертируя str в int
# и убирая лишнюю единицу, т.к. в программах файлы нумеруют с 1,
# а у нас здесь индексы идут с 0
BondInd.append(np.array(words[:2], dtype=int)-1)
# а численное значение сохраняем отдельно, конвертируя str во float
BondOrd.append(float(words[2]))
inpf.close() # ну и закрываем файл
# открываем файл, куда будем всё писать, назовём его 'fig.tex'
outf = open("fig.tex", "w")
# это функция для строки, которая рисует связь в TikZ
# берёт два индекса, номера атомов из BondInd[n], i и j,
# а также значение порядка связи (bond order = bo).
def DrawBond(i,j,bo):
res = '\draw [ultra thick] '
res += ' (%7.4f,%7.4f) -- ' % (xyz[i][0],xyz[i][1]) # начало вектора
res += ' (%7.4f,%7.4f) ' % (xyz[j][0],xyz[j][1]) # конец вектора
res += ' node [pos=0.5,below] {%7.1f};' % (bo) # и подпись
return res
# Эти штуки мы считаем, чтобы получить перспективу
# берём среднее значение координаты z, чтобы
# получить референсное значение для перспективы
AvZ = np.mean([r[2] for r in xyz])
# и считаем амплитуду для координаты Z
ZAmp = np.abs(max([r[2] for r in xyz]) - min([r[2] for r in xyz]))
# молекула может быть плоской и вся лежать в плоскости XY,
# поэтому если изменение координаты Z слишком мало, то делить на околонулевое
# значение, наверное, не стоит. Поэтому ставим такой нижний порог на амплитуду,
# в 0.5 ангстрем
ZAmp = max(0.5,ZAmp)
# а это функция для рисования атома в виде шарика,
# нам нужен только индекс атома, i
def DrawAtom(i):
res = '\draw'
if atn[i] == 'c': # это мы рисуем углерод
Rad = 0.7 # ковалентный радиус углерода, в ангстремах
res += '[atomC] '
elif atn[i] == 'h': # это мы рисуем углерод
Rad = 0.25 # ковалентный радиус водорода, в ангстремах
res += '[atomH] '
else: # а это для не заданных атомов, какие-то рандомные настройки
Rad = 0.5
res += '[atomX3] '
# позиция атома -- это проекция на плоскось xy
x = xyz[i][0] # x-координата
y = xyz[i][1] # y-координата
# а это радиус атома на картинке, который зависит от перспективы
r = Rad * 0.3 * (1.0 + 0.9 * (xyz[i][2] - AvZ)/ZAmp)
res += '(%7.4f,%7.4f) circle (%.3f);' % (x,y, r)
return res
# собственно, это 'шапка' LaTeX-овского документа
# с настройками TikZ
# здесь мы задаём параметры для атомов C и H, но их можно и
# надобавлять других
HeadFile=r"""\documentclass{article}
\usepackage[utf8]{inputenc}
\usepackage{tikz}
\usepackage{xcolor}
\usepackage{color}
\begin{document}
\begin{center}
\begin{tikzpicture}[
>=stealth,
atomC/.style={shade, ball color=gray!50!black},
atomH/.style={shade, ball color=white!50!gray},
atomX3/.style={shade, ball color=orange!50!white},
scale=1.
]
"""
# а это низ LaTeX-овского документа
TailFile='''
\end{tikzpicture}
\end{center}
\end{document}
'''
# теперь начинаем запись LaTeX-овского документа
outf.write(HeadFile) # начинаем с шапки
# потом идём по всем связям
for n,bo in enumerate(BondOrd):
# при помощи функции DrawBond получаем
# TikZ команду для рисования связи
line = DrawBond(BondInd[n][0],BondInd[n][1],bo)
outf.write(line+"\n")
# а теперь рисуем поверх шарики атомов
for n in range(0,len(atn)):
line = DrawAtom(n)
outf.write(line+"\n")
# не забываем низ файла.
outf.write(TailFile)
outf.close() # и закрыть файл
Этот монстр создаст файл fig.tex из файлов mol.xyz и bonds.dat.
Содержимое этого кода тупо, банально и плохо написано, но всё же прокомментируем что он делает.
Сначала он читает геометрию молекулы и связи в этой молекулы, заданные в наших файлах mol.xyz и bonds.dat. Складируем это всё в несколько списков.
Выкатывем шапку LaTeX-овского документа в файл fig.tex, которые и является нашим искомым результатом.
Начинаем генерировать команды построения связей, каркас молекулы. Для этого у нас есть команды TikZ вида \draw [ultra thick] (x1,y1) -- (x2,y2) node [pos=0.5,below] {WBO}; Эта команда рисует линию от точки (x1,y1) к точке (x2,y2), а ещё посередине линии (pos=0.5 -- это позиция на половине, снизу) выдаст надпись WBO. В принципе, этого достаточно уже для наших целей, но в целях дополнительного украшательства есть следующий шаг.
Сверху позиций атомов нарисуем шарики, да не просто так, а с перспективой. Для этого нам нужна команда вида \draw[atomType] (x,y) circle (r); atomType -- это стиль шарика, который мы пре-задали в шапке LaTeX-овского документа, поскольку у нас только углерод и водород, их только мы и определили. (x,y) -- это позиция центра шара (проекция молекулы на плоскость xy). Ну а r -- это радиус шара, с помощью которого мы создаём перспективу, отображая ось z на рисунке. То, как мы вычисляем этот радиус поговорим ниже.
Ну и в конце добавляем "хвост" LaTeX-овского документа, чтобы он у нас вообще скомпилировался.
В результате мы получаем LaTeX-овский код в файле fig.tex с картинкой, генерируемой пакетом TikZ.
\documentclass{article}
\usepackage[utf8]{inputenc}
\usepackage{tikz}
\usepackage{xcolor}
\usepackage{color}
\begin{document}
\begin{center}
\begin{tikzpicture}[
>=stealth,
atomC/.style={shade, ball color=gray!50!black},
atomH/.style={shade, ball color=white!50!gray},
atomX3/.style={shade, ball color=orange!50!white},
scale=1.
]
\draw [ultra thick] ( 1.7034, 2.7712) -- ( 0.8653, 2.1947) node [pos=0.5,below] { 1.3};
\draw [ultra thick] ( 1.3589, 3.9361) -- ( 0.1559, 4.5930) node [pos=0.5,below] { 1.3};
\draw [ultra thick] ( 2.5532, 4.6066) -- ( 2.6149, 5.9736) node [pos=0.5,below] { 1.3};
\draw [ultra thick] ( 3.6359, 3.8562) -- ( 4.8441, 4.4286) node [pos=0.5,below] { 1.3};
\draw [ultra thick] ( 3.1107, 2.7218) -- ( 3.7627, 2.0930) node [pos=0.5,below] { 1.3};
\draw [ultra thick] ( 0.8653, 2.1947) -- ( 1.7034, 2.7712) node [pos=0.5,below] { 1.3};
\draw [ultra thick] ( 0.1559, 4.5930) -- ( 1.3589, 3.9361) node [pos=0.5,below] { 1.3};
\draw [ultra thick] ( 3.7627, 2.0930) -- ( 3.1107, 2.7218) node [pos=0.5,below] { 1.3};
\draw [ultra thick] ( 4.8441, 4.4286) -- ( 3.6359, 3.8562) node [pos=0.5,below] { 1.3};
\draw [ultra thick] ( 2.6149, 5.9736) -- ( 2.5532, 4.6066) node [pos=0.5,below] { 1.3};
\draw [ultra thick] (-0.4602, 2.7379) -- (-0.7957, 3.8720) node [pos=0.5,below] { 1.6};
\draw [ultra thick] (-0.7957, 3.8720) -- (-0.4602, 2.7379) node [pos=0.5,below] { 1.6};
\draw [ultra thick] ( 0.1725, 5.9631) -- ( 1.3353, 6.6160) node [pos=0.5,below] { 1.6};
\draw [ultra thick] ( 1.3353, 6.6160) -- ( 0.1725, 5.9631) node [pos=0.5,below] { 1.6};
\draw [ultra thick] ( 3.9295, 6.5250) -- ( 4.9836, 5.7944) node [pos=0.5,below] { 1.6};
\draw [ultra thick] ( 4.9836, 5.7944) -- ( 3.9295, 6.5250) node [pos=0.5,below] { 1.6};
\draw [ultra thick] ( 1.5356, 1.3545) -- ( 2.9057, 1.3064) node [pos=0.5,below] { 1.6};
\draw [ultra thick] ( 2.9057, 1.3064) -- ( 1.5356, 1.3545) node [pos=0.5,below] { 1.6};
\draw [ultra thick] ( 5.1074, 2.5426) -- ( 5.6188, 3.6470) node [pos=0.5,below] { 1.6};
\draw [ultra thick] ( 5.6188, 3.6470) -- ( 5.1074, 2.5426) node [pos=0.5,below] { 1.6};
\draw [ultra thick] (-1.1987, 2.2941) -- (-0.4602, 2.7379) node [pos=0.5,below] { 1.0};
\draw [ultra thick] (-1.7876, 4.2850) -- (-0.7957, 3.8720) node [pos=0.5,below] { 1.0};
\draw [ultra thick] (-0.7487, 6.5290) -- ( 0.1725, 5.9631) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 1.2927, 7.6752) -- ( 1.3353, 6.6160) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 4.0765, 7.5776) -- ( 3.9295, 6.5250) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 5.9270, 6.2949) -- ( 4.9836, 5.7944) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 0.9430, 0.8096) -- ( 1.5356, 1.3545) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 3.3483, 0.7252) -- ( 2.9057, 1.3064) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 5.7110, 2.0517) -- ( 5.1074, 2.5426) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 6.6087, 3.9905) -- ( 5.6188, 3.6470) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 1.7034, 2.7712) -- ( 3.1107, 2.7218) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 1.3589, 3.9361) -- ( 2.5532, 4.6066) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 2.5532, 4.6066) -- ( 3.6359, 3.8562) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 3.6359, 3.8562) -- ( 2.5532, 4.6066) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 3.1107, 2.7218) -- ( 1.7034, 2.7712) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 0.8653, 2.1947) -- ( 1.5356, 1.3545) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 0.1559, 4.5930) -- (-0.7957, 3.8720) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 3.7627, 2.0930) -- ( 2.9057, 1.3064) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 4.8441, 4.4286) -- ( 4.9836, 5.7944) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 2.6149, 5.9736) -- ( 3.9295, 6.5250) node [pos=0.5,below] { 1.2};
\draw [ultra thick] (-0.4602, 2.7379) -- ( 0.8653, 2.1947) node [pos=0.5,below] { 1.2};
\draw [ultra thick] (-0.7957, 3.8720) -- ( 0.1559, 4.5930) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 0.1725, 5.9631) -- ( 0.1559, 4.5930) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 1.3353, 6.6160) -- ( 2.6149, 5.9736) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 3.9295, 6.5250) -- ( 2.6149, 5.9736) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 4.9836, 5.7944) -- ( 4.8441, 4.4286) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 1.5356, 1.3545) -- ( 0.8653, 2.1947) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 2.9057, 1.3064) -- ( 3.7627, 2.0930) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 5.1074, 2.5426) -- ( 3.7627, 2.0930) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 5.6188, 3.6470) -- ( 4.8441, 4.4286) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 1.7034, 2.7712) -- ( 1.3589, 3.9361) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 1.3589, 3.9361) -- ( 1.7034, 2.7712) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 2.5532, 4.6066) -- ( 1.3589, 3.9361) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 3.6359, 3.8562) -- ( 3.1107, 2.7218) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 3.1107, 2.7218) -- ( 3.6359, 3.8562) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 0.8653, 2.1947) -- (-0.4602, 2.7379) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 0.1559, 4.5930) -- ( 0.1725, 5.9631) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 3.7627, 2.0930) -- ( 5.1074, 2.5426) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 4.8441, 4.4286) -- ( 5.6188, 3.6470) node [pos=0.5,below] { 1.2};
\draw [ultra thick] ( 2.6149, 5.9736) -- ( 1.3353, 6.6160) node [pos=0.5,below] { 1.2};
\draw [ultra thick] (-0.4602, 2.7379) -- (-1.1987, 2.2941) node [pos=0.5,below] { 1.0};
\draw [ultra thick] (-0.7957, 3.8720) -- (-1.7876, 4.2850) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 0.1725, 5.9631) -- (-0.7487, 6.5290) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 1.3353, 6.6160) -- ( 1.2927, 7.6752) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 3.9295, 6.5250) -- ( 4.0765, 7.5776) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 4.9836, 5.7944) -- ( 5.9270, 6.2949) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 1.5356, 1.3545) -- ( 0.9430, 0.8096) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 2.9057, 1.3064) -- ( 3.3483, 0.7252) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 5.1074, 2.5426) -- ( 5.7110, 2.0517) node [pos=0.5,below] { 1.0};
\draw [ultra thick] ( 5.6188, 3.6470) -- ( 6.6087, 3.9905) node [pos=0.5,below] { 1.0};
\draw[atomC] ( 1.7034, 2.7712) circle (0.199);
\draw[atomC] ( 1.3589, 3.9361) circle (0.168);
\draw[atomC] ( 2.5532, 4.6066) circle (0.153);
\draw[atomC] ( 3.6359, 3.8562) circle (0.175);
\draw[atomC] ( 3.1107, 2.7218) circle (0.204);
\draw[atomC] ( 0.8653, 2.1947) circle (0.241);
\draw[atomC] ( 0.1559, 4.5930) circle (0.175);
\draw[atomC] ( 3.7627, 2.0930) circle (0.250);
\draw[atomC] ( 4.8441, 4.4286) circle (0.190);
\draw[atomC] ( 2.6149, 5.9736) circle (0.144);
\draw[atomC] (-0.4602, 2.7379) circle (0.241);
\draw[atomC] (-0.7957, 3.8720) circle (0.210);
\draw[atomC] ( 0.1725, 5.9631) circle (0.157);
\draw[atomC] ( 1.3353, 6.6160) circle (0.142);
\draw[atomC] ( 3.9295, 6.5250) circle (0.151);
\draw[atomC] ( 4.9836, 5.7944) circle (0.172);
\draw[atomC] ( 1.5356, 1.3545) circle (0.282);
\draw[atomC] ( 2.9057, 1.3064) circle (0.287);
\draw[atomC] ( 5.1074, 2.5426) circle (0.259);
\draw[atomC] ( 5.6188, 3.6470) circle (0.231);
\draw[atomH] (-1.1987, 2.2941) circle (0.096);
\draw[atomH] (-1.7876, 4.2850) circle (0.077);
\draw[atomH] (-0.7487, 6.5290) circle (0.057);
\draw[atomH] ( 1.2927, 7.6752) circle (0.047);
\draw[atomH] ( 4.0765, 7.5776) circle (0.051);
\draw[atomH] ( 5.9270, 6.2949) circle (0.064);
\draw[atomH] ( 0.9430, 0.8096) circle (0.112);
\draw[atomH] ( 3.3483, 0.7252) circle (0.115);
\draw[atomH] ( 5.7110, 2.0517) circle (0.104);
\draw[atomH] ( 6.6087, 3.9905) circle (0.087);
\end{tikzpicture}
\end{center}
\end{document}
Теперь пару слов о перспективе. Радиусы атомов (r) вычисляются из z-координат атомов по формуле
Параметр R0 -- это изначальный радиус атома, в качестве него я выбрал ковалентные радиусы углерода (0.7 Å) и водорода (0.25 Å). 0.3 и 0.9 -- просто подгоночные параметры, A -- это разность между максимальным и минимальным значением координат z всех атомов, а ⟨z⟩ -- это среднее значение всех координат атомов, оно нужно чтобы в зависимости от расположения молекулы вдоль оси z у нас не уменьшались/увеличивались все размеры шариков. Естественно, молекула может оказаться плоской, и мы можем расположить её всю в плоскости xy, тогда параметр A окажется равным нулю, поэтому чтобы избежать деления на 0, мы задаём минимально возможное значение этого параметра, равное 0.5 Å.
Полученную последовательность команд мы можем обернуть в простейший Bash-евский скрипт.
#! /bin/bash
python3 make_tikz_picture_bond_orders.py
pdflatex fig.tex
evince fig.pdf &А вот и получившаяся картинка. В принципе, её можно редактировать как угодно: можно подправить TikZ-овский код, а можно её открыть в каком-нибудь Inkscape и допилить руками. Такое может быть даже проще и веселее.
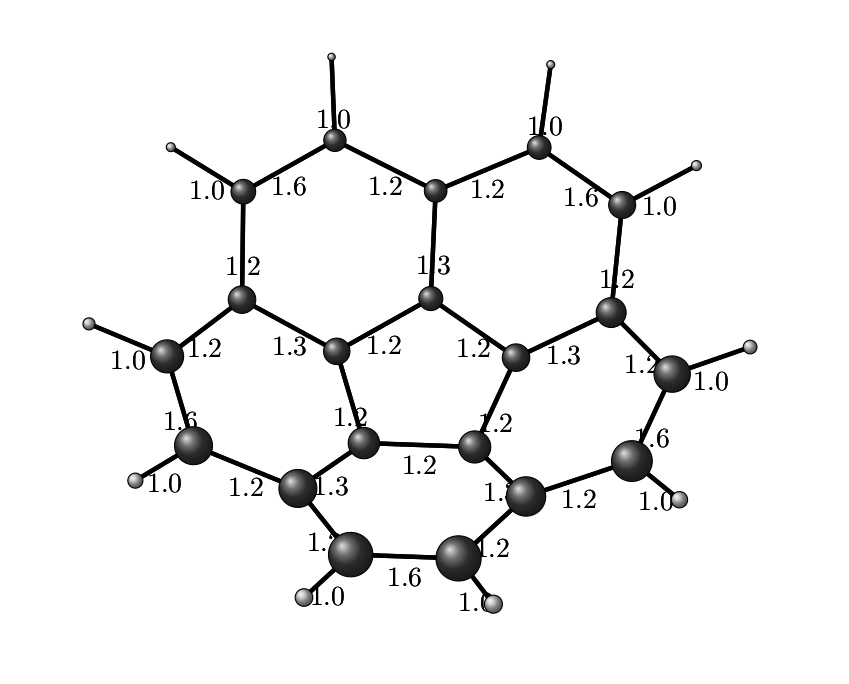
Конечно, полученный результат всё ещё самопальный отстой, но его можно допилить до ума средствами как самих Python-а/TikZ, так и постфактум, открыв pdf-ку в том же Inkscape. Но суть не в этом, главное, что из говна и палок всегда можно соорудить что-нибудь :) Не уверен, что это достойный вывод, но как-то ничего другого в голову сейчас не лезет.
Ну и естественно, это всё мы можем применить и для куда больших монстров, например, молекул из этой вот статьи, типа C50H20.
70
energy: -117.275352008181 gnorm: 0.000390187477 xtb: 6.3.3 (5b13467)
C -2.68077703943328 -2.91238079355590 0.68845892053073
C 0.27128316214264 0.37286677181363 -2.74314008247056
C 0.60507213164374 1.63822103018138 -2.32805604984469
C 1.14470546196813 -0.70663678298366 -2.43469769398305
C -1.06581084645995 -0.07976153594376 -2.56809812472648
C 1.77225930946232 3.34194992574212 -1.35390644484119
C -1.98283643251999 0.76217241732452 -1.98927003080863
C -1.01875800399212 -1.43900401441490 -2.15147212967076
C -3.55692461220946 -1.82950667221932 0.37905630355287
C -1.89176373398147 -1.86860332754445 -1.18289723879776
C 0.34741614781742 -1.82643527040481 -2.06902919428710
C -3.67216311210816 1.49892949580444 -0.64117931120830
C 0.75242813633749 -2.61847110182269 -1.02333569383271
C 2.29555737015994 -0.45112940559788 -1.73107322169934
C -2.87238808071641 2.62222207085053 -1.00799627676733
C 0.66463461520378 -3.86112902965567 0.89031958102536
C -0.18920704342200 -3.24531710310039 -0.12895583438488
C 2.05676673592769 -2.48502136815445 -0.42298550587013
C 3.95825068512170 -0.66497090027774 -0.18068279856657
C -1.69755571565036 2.15512408221106 -1.74879321174699
C -3.03679366568025 0.27415234921752 -1.13455439255542
C 2.00590199441865 -3.40709107355358 0.71472798937060
C -2.99082756412136 -1.05357171075259 -0.72758318373668
C -1.52370227486734 -2.86686273094032 -0.20948195675439
C -0.39146450717046 2.59725613007549 -1.91977290964893
C 3.91104920579450 0.69851566956800 -0.59860294748331
C 1.90335653160282 1.94647130553701 -1.78127674351813
C 0.40182204522241 3.73059083372130 -1.43661584908383
C 2.83556608650419 -1.39118412041965 -0.78017032846857
C 2.75652657231956 0.89199780089277 -1.47998501347163
H 0.71897816971423 6.94953967009544 -0.48148528448535
C 4.99431155891219 -1.09605306896690 0.62471035753650
C 2.72105457751250 4.26653693910675 -0.96296095556863
C 2.69348079643417 -4.80311075070405 2.53786543979124
C 0.04038665207252 5.02674475351316 -1.12474813797369
C 3.00350369902655 -3.89222211250683 1.53774104921398
H -4.82042850461680 5.07437609405038 0.24363138915910
H -4.49373585157531 -4.36091811325598 3.13578717982119
C 0.37989353033973 -4.78035006216538 1.88121158570339
C -3.03143028976537 -3.81288232917844 1.67539943210881
H 5.07666322596571 -2.12973220473117 0.91419866700697
H 1.16610201764482 -5.96608912900056 3.47724162265726
C 1.39404265134009 -5.24298807813292 2.70798189193439
C -4.22237245502503 -3.65015380568231 2.36912651549759
C -4.74523454500569 -1.69470802282653 1.07018658671297
H -6.00451448165837 -2.49367353365328 2.60227071341764
C -4.86275930627008 1.69930182583409 0.02982253863623
H -0.61535214349515 -5.17261507331524 2.00242406849407
C -3.29834565540937 3.89653803853535 -0.68769832762239
C 4.90198296445000 1.57101884068675 -0.19276970635118
H -2.73557885272309 4.76143849008124 -0.99481217498725
C -4.48985271871798 4.07512095504141 0.00114134487655
H 6.70052705225601 1.80716708714242 0.93899270887624
H 3.08207991140213 6.27938902195787 -0.33886179434377
C 1.00704259699109 5.93589682978381 -0.71842348790248
H -0.97982786218491 5.35578076402524 -1.22462642034273
C -5.26468521546126 2.98685996970108 0.35651988760019
H -5.50538400831336 0.87121774308353 0.27556339882176
H 4.02976647919106 -3.60017823056423 1.39430701088472
H 3.47890531662068 -5.18317486268750 3.17445966634839
H 3.76631271635534 4.00982807793270 -0.93818051057439
C 2.33474085104098 5.55937632045060 -0.63829226138629
H -5.44356464835715 -0.91358199001587 0.82268906061483
C -5.07119650320345 -2.60105093221218 2.06937269377368
H -6.19951205810888 3.13743613055288 0.87615264205200
H 6.78191855437962 -0.54394998060052 1.65962919313397
C 5.92542821547799 1.12146646469345 0.62975329785856
H 4.91319519878343 2.59233680788850 -0.53315466435521
H -2.40926221725034 -4.66382359262515 1.89422285207033
C 5.97115702191632 -0.19949789292965 1.03464030503872 1 40 1.425
2 3 1.377
3 2 1.377
4 14 1.377
5 7 1.377
6 33 1.425
7 5 1.377
8 10 1.377
9 45 1.425
10 8 1.377
11 13 1.377
12 47 1.425
13 11 1.377
14 4 1.377
15 49 1.425
16 39 1.425
17 24 1.471
18 29 1.471
19 32 1.425
20 25 1.471
21 23 1.471
22 36 1.425
23 21 1.471
24 17 1.471
25 20 1.471
26 50 1.425
27 30 1.471
28 35 1.425
29 18 1.471
30 27 1.471
31 55 0.971
32 19 1.425
33 6 1.425
34 43 1.446
35 28 1.425
36 22 1.425
37 52 0.971
38 44 0.971
39 16 1.425
40 1 1.425
41 32 0.955
42 43 0.971
43 34 1.446
44 64 1.446
45 9 1.425
46 64 0.971
47 12 1.425
48 39 0.955
49 15 1.425
50 26 1.425
51 49 0.955
52 57 1.446
53 67 0.971
54 62 0.971
55 62 1.446
56 35 0.955
57 52 1.446
58 47 0.955
59 36 0.955
60 34 0.971
61 33 0.955
62 55 1.446
63 45 0.955
64 44 1.446
65 57 0.971
66 70 0.971
67 70 1.446
68 50 0.955
69 40 0.955
70 67 1.446
1 9 1.268
2 4 1.162
3 27 1.167
4 2 1.162
5 8 1.162
6 28 1.268
7 21 1.167
8 5 1.162
9 1 1.268
10 24 1.167
11 8 1.162
12 15 1.268
13 17 1.167
14 30 1.167
15 12 1.268
16 22 1.268
17 13 1.167
18 13 1.167
19 26 1.268
20 7 1.167
21 7 1.167
22 16 1.268
23 10 1.167
24 10 1.167
25 3 1.167
26 19 1.268
27 3 1.167
28 6 1.268
29 14 1.167
30 14 1.167
32 70 1.415
33 62 1.415
34 36 1.415
35 55 1.415
36 34 1.415
39 43 1.415
40 44 1.415
43 39 1.415
44 40 1.415
45 64 1.415
47 57 1.415
49 52 1.415
50 67 1.415
52 49 1.415
55 35 1.415
57 47 1.415
62 33 1.415
64 45 1.415
67 50 1.415
70 32 1.415
1 24 1.081
2 5 1.162
3 25 1.167
4 11 1.162
5 2 1.162
6 27 1.081
7 20 1.167
8 11 1.162
9 23 1.081
10 23 1.167
11 4 1.162
12 21 1.081
13 18 1.167
14 29 1.167
15 20 1.081
16 17 1.081
17 16 1.081
18 22 1.081
19 29 1.081
20 15 1.081
21 12 1.081
22 18 1.081
23 9 1.081
24 1 1.081
25 28 1.081
26 30 1.081
27 6 1.081
28 25 1.081
29 19 1.081
30 26 1.081
33 61 0.955
34 60 0.971
35 56 0.955
36 59 0.955
39 48 0.955
40 69 0.955
43 42 0.971
44 38 0.971
45 63 0.955
47 58 0.955
49 51 0.955
50 68 0.955
52 37 0.971
55 31 0.971
57 65 0.971
62 54 0.971
64 46 0.971
67 53 0.971
70 66 0.971