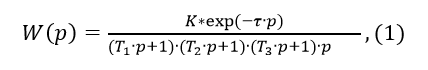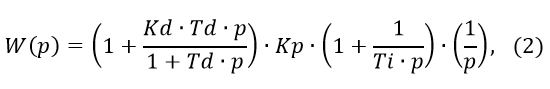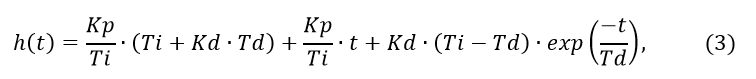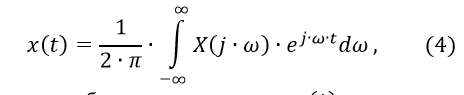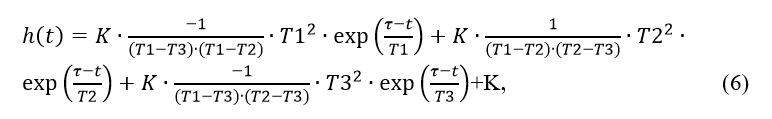https://habrahabr.ru/post/346338/- Разработка под Windows
- Математика
- Анализ и проектирование систем
- Python
 Здравствуйте!
Здравствуйте!
До настоящего времени в арсенале средств высокоуровневого языка программирования Python отсутствовали модули для численного преобразования передаточных функций элементов САУ из частотной области во временную.
Поскольку функции обратного преобразования Лапласа широко используются при анализе динамических систем контроля измерения и управления, использование Python для указанных целей было весьма затруднительно, поскольку приходилось использовать менее точное обратное Фурье преобразование [1].
Указанную проблему решает модуль mpmath библиотеки Python свободного распространения (под лицензией BSD), предназначенный для решения задач вещественной и комплексной арифметики с плавающей точкой и заданной точностью.
Работу над модулем ещё в 2007 году начал Fredrik Johansson [2], и, благодаря помощи многих участников проекта, в настоящее время mpmath приобрёл возможности серьёзного математического пакета.
Однако нас будет интересовать только заявленная в статье тема, реализуемая при помощи одношагового алгоритма invertlaplace. В качестве примера рассмотрим сравнение результатов обратного преобразования Лапласа передаточной функции w(p)=1/(1+p)** 2 при помощи invertlaplace с известной переходной функцией h(t)=e**-t от указанной передаточной функции:
Тестирование invertlaplacefrom mpmath import *
import time
mp.dps = 15#число членов, используемых в приближении
mp.pretty = True
start = time.time()
def run_invertlaplace(tt,fp,ft):
for i in range(0,len(tt)):
print('Значение тестовой функции : %s'%ft(tt[i]))
print('Полученное значение функции : %s'%invertlaplace(fp,tt[i],method='talbot'))
print(' Значение h(t) : %s. Абсолютная погрешность :%s.'%(ft(tt[i]), ft(tt[i])-invertlaplace(fp,tt[i],method='talbot')))
stop = time.time()
print ("Время, затраченное на обратное преобразование Лапласа: %s"%(stop-start))
tt = [0.001, 0.01, 0.1, 1, 10]#список значений отсчётов времени
fp = lambda p: 1/(p+1)**2#передаточная функция частоты для тестирования программы
ft = lambda t: t*exp(-t)# переходная функция времени для тестирования программы
run_invertlaplace(tt,fp,ft)
Результаты тестирования:
Значение тестовой функции: 0.000999000499833375
Полученное значение функции: 0.000999000499833375
Значение h(t): 0.000999000499833375. Абсолютная погрешность :8.57923043561212e-20.
Значение тестовой функции: 0.00990049833749168
Полученное значение функции: 0.00990049833749168
Значение h(t): 0.00990049833749168. Абсолютная погрешность :3.27007646698047e-19.
Значение тестовой функции: 0.090483741803596
Полученное значение функции: 0.090483741803596
Значение h(t): 0.090483741803596. Абсолютная погрешность: -1.75215800052168e-18.
Значение тестовой функции: 0.367879441171442
Полученное значение функции: 0.367879441171442
Значение h(t): 0.367879441171442. Абсолютная погрешность :1.2428864009344e-17.
Значение тестовой функции: 0.000453999297624849
Полученное значение функции: 0.000453999297624849
Значение h(t): 0.000453999297624849. Абсолютная погрешность :4.04513489306658e-20.
Время, затраченное на обратное преобразование Лапласа: 0.18808794021606445
Тестовый пример ограничен по объёму, но и на нём видно, что одношаговый алгоритм invertlaplace имеет высокую точность и не критичное время выполнения для ограниченного числа значений времени.
В рассмотренном примере был использован метод talbot, об особенностях других методов можно прочесть в документации [3].
Однако следует учитывать, что все численные методы обратного преобразования Лапласа требуют, чтобы их абсцисса сдвигалась ближе к началу координат для больших времен. Если абсцисса сдвинется влево от самой правой координаты в области Лапласа, ответ будет совершенно неверным.
Поэтому необходимо провести исследование применимости численного обратного преобразования Лапласа для определённых передаточных функций и оценить погрешность в сравнении с другим методом, в данной публикации это метод обратного преобразования Фурье.
1. Построение переходной характеристики объекта управления по его передаточной функции с использованием invertlaplace
Допустим, у нас есть водно-водяной теплообменник с передаточной функцией по каналу, температура нагреваемой воды – расход греющей воды. Передаточная функция такого объекта управления от единичного возмущения по расходу греющей воды с учётом запаздывания τ имеет следующий вид:
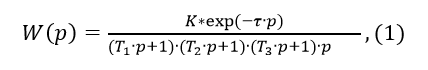
где: Ti – постоянные времени звеньев; K – статический коэффициент передачи; p ¬ оператор Лапласа.
Обратное преобразование Лапласа передаточной функции(1)# -*- coding: utf8 -*-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from mpmath import *
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
mp.dps = 5; mp.pretty = True
def run_invertlaplace(tt,fp,tau):
y=[]
for i in np.arange(0,len(tt)):
if tt[i]<=tau:
y.append(0)
else:
y.append(invertlaplace(fp,tt[i],method='talbot'))
return y
tau=5
tt = np.arange(0,100,0.05)
T1=5;T2=4;T3=4;K=1.5;tau=14
fp = lambda p: K*exp(-tau*p)/((T1*p+1)*(T2*p+1)*(T3*p+1)*p)
y=run_invertlaplace(tt,fp,tau)
plt.title('Переходная характеристика объекта управления \n, полученная через invertlaplace ')
plt.plot(tt,y,'r')
plt.grid(True)
plt.show()
Получим переходную характеристику объекта с запаздыванием и самовыравниванием:
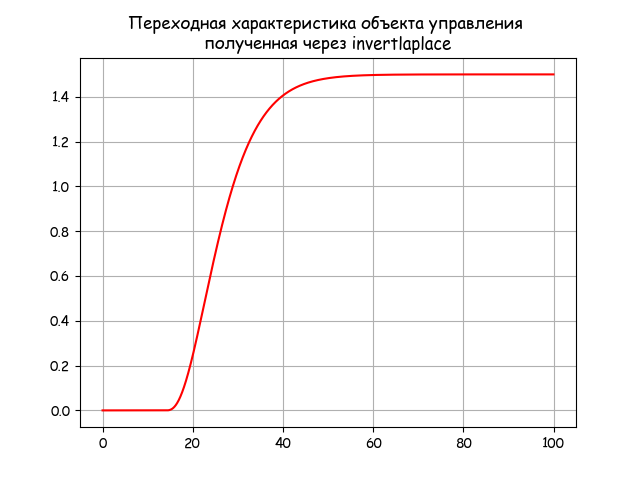
2. Построение переходной характеристики ПИД- регулятора по его передаточной функции с использованием invertlaplace
Изображение по Лапласу передаточной функции ПИД регулятора имеет вид:
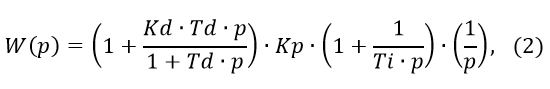
где: Td, Ti – постоянные времени, дифференцирующего и интегрирующего звеньев; Kp, Kd – статические коэффициенты передачи пропорционального и дифференцирующего звеньев;
p – оператор Лапласа.
Обратное преобразование Лапласа передаточной функции(2)# -*- coding: utf8 -*-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from mpmath import *
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
mp.dps = 5; mp.pretty = True
tt = np.arange(0.01,20,0.05)
Kp=2;Ti=2;Kd=4;Td=0.5
fp = lambda p: (1+(Kd*Td*p)/(1+Td*p))*Kp*(1+1/(Ti*p))*(1/p)
y=[invertlaplace(fp,tt[i],method='talbot') for i in np.arange(0,len(tt))]
Kd=0
fp = lambda p: (1+(Kd*Td*p)/(1+Td*p))*Kp*(1+1/(Ti*p))*(1/p)
y1=[invertlaplace(fp,tt[i],method='talbot') for i in np.arange(0,len(tt))]
plt.title('Переходные характеристики регуляторов \n, полученные через invertlaplace ')
plt.plot(tt,y,'r', color='r',linewidth=2, label='ПИД-регулятор')
plt.plot(tt,y1, color='b', linewidth=2, label='ПИ-регулятор')
plt.grid(True)
plt.legend(loc='best')
plt.show()
По приведенному листингу можно получить не только переходную характеристику ПИД- регулятора, но и ПИ-регулятора, приняв Kd=0:
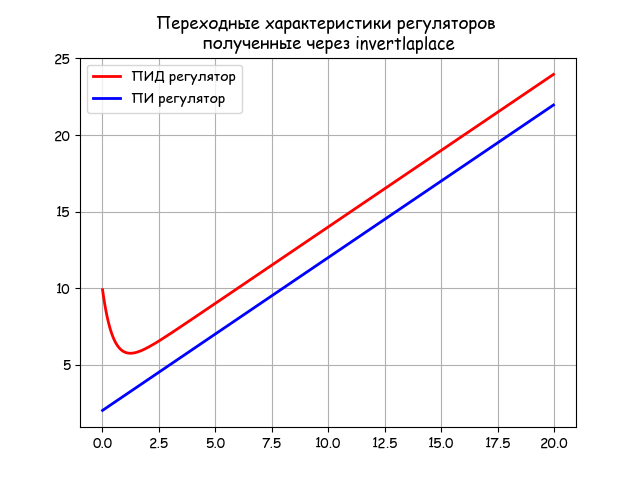
3. Оценка точности численного метода обратного преобразования Лапласа invertlaplace применительно к типовым объектам САУ
С учётом предостережений относительно применимости invertlaplace, приведенных в начале статьи, в дальнейшем изложении была доказана применимость метода к объектам с запаздыванием и самовыравниванием, а так же к регуляторам.
Остаётся до конца не выясненным вопрос точности численного решения. Для внесения ясности воспользуемся передаточной функцией (2) и следующим точным её преобразованием в переходную функцию, приведённую в [1]:
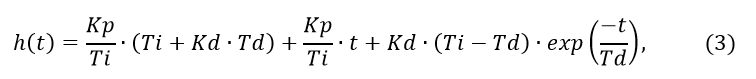
Точность обратного преобразования (2) с использованием тестовой функции (3)# -*- coding: utf8 -*-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from mpmath import *
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
mp.dps = 15; mp.pretty = True
tt = np.arange(0.01,20,0.01)
Kp=2;Ti=2;Kd=4;Td=0.5
fp = lambda p: (1+(Kd*Td*p)/(1+Td*p))*Kp*(1+1/(Ti*p))*(1/p)
ft = lambda t:(Kp/Ti)*(Ti+Kd*Td)+(Kp/Ti)*t+Kd*(Ti-Td)*exp(-t/Td)
y=np.array([invertlaplace(fp,tt[i],method='talbot') for i in np.arange(0,len(tt))])
y1=np.array([ft(tt[i]) for i in np.arange(0,len(tt))])
z=y-y1
plt.title('Оценка точности invertlaplace ')
plt.plot(tt,z,'r', color='r',linewidth=1, label='Разница между точным и численным решением')
plt.grid(True)
plt.legend(loc='best')
plt.show()
Получим следующий график:
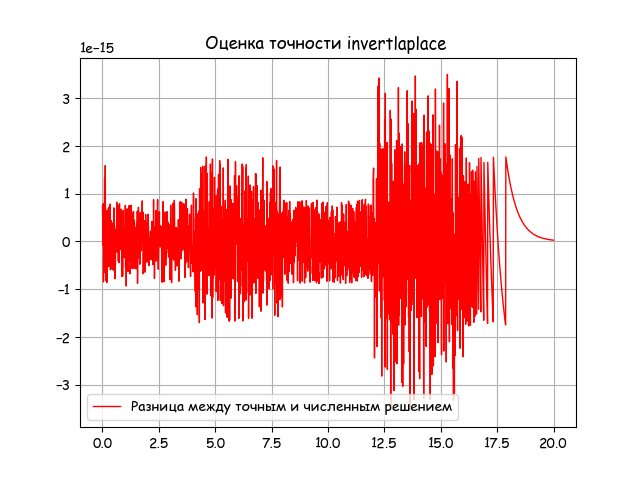
Из графика видно, что погрешность численного метода для приведенного класса передаточных функций пренебрежимо мала (3*10^-15). Кроме того, погрешностью численного метода можно управлять, устанавливая значения mp.dps и шаг tt[i+1]-tt[i] (см. листинг).
4. Сравнительная оценка точности численного метода обратного преобразования Лапласа invertlaplace и численного метода обратного преобразования Фурье применительно к типовым объектам САУ
Построение переходной характеристики можно произвести на основе формулы обратного преобразования Фурье [1]:
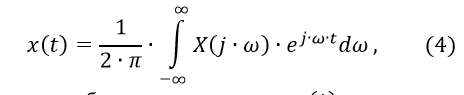
где Re(W(j∙ω))— вещественная частотная характеристика объекта регулирования.
В качестве верхнего предела интегрирования θв в расчете берется значение частоты ωс, при котором модуль Re(W(j∙ω)) уменьшается до некоторого малого значения (например, 0,05*K) и не превосходит это значение при дальнейшем возрастании ω.
Вначале определим верхний предел интегрирования в соотношении (5). Для этого воспользуемся передаточной функцией (1), предварительно избавившись от единичного воздействия, умножив правую часть на оператор p.
Построение графика функции Re(W(j∙ω))# -*- coding: utf8 -*-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from mpmath import *
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
ww= np.arange(0,0.6,0.005)
T1=25;T2=21;T3=12;K=0.37;tau=14
def invertfure(w):
j=(-1)**0.5
return ((K*np.exp(-tau*j*w)/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))).real)
z=[invertfure(w) for w in ww]
plt.title('Зависимость вещественной части передаточной функции \n объекта управления Re(W(j*w)) от частоты ')
plt.plot(ww,z,'r')
plt.grid(True)
plt.show()
График:
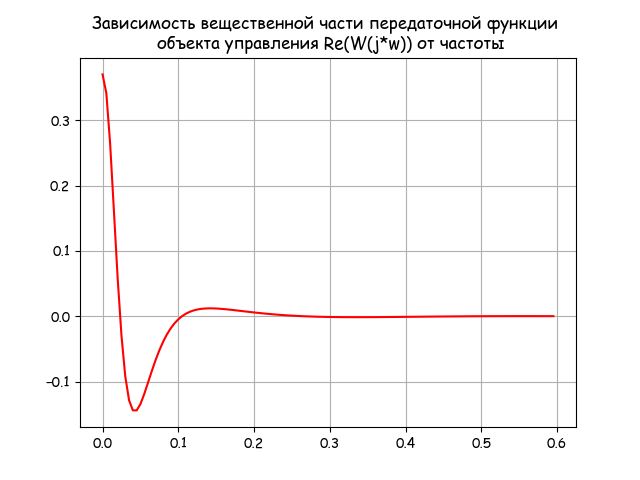
Из графика видно, что верхний предел интегрирования в соотношении (5) может быть принят равным 0.6, поскольку при дальнейшем увеличении частоты вещественная часть передаточной функции объекта управления сохраняет нулевое значение.
Используя (5), получим переходную характеристику объекта управления методом обратного преобразования Фурье:
Переходная характеристика по Фурье# -*- coding: utf8 -*-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from mpmath import *
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
from scipy.integrate import quad
tt=np.arange(0,200,1)
T1=25;T2=21;T3=12;K=0.37;tau=14
def invertfure(w,t):
j=(-1)**0.5
return (2/np.pi)*((K*np.exp(-tau*j*w)/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))).real*(np.sin(w*t)/w))
z=[quad(lambda w: invertfure(w,t),0, 0.6)[0] for t in tt]
plt.title('Переходная характеристика объекта управления, полученная \n методом обратного преобразования Фурье')
plt.plot(tt,z,'r')
plt.grid(True)
plt.show()
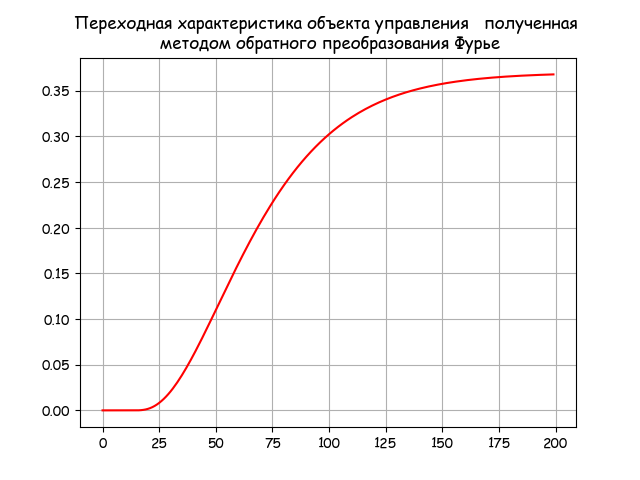
Для сравнительной оценки точности обратного преобразования Лапласа и Фурье, воспользуемся точным преобразованием передаточной функции (1) объекта управления приведенном в [1]:
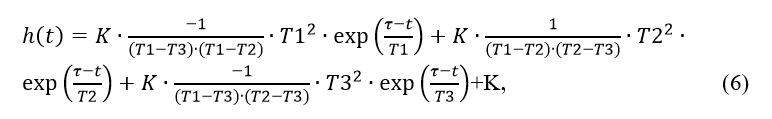
Из точного преобразования (6) вычтем по очереди обратное преобразование (1) Лапласа и обратное преобразование Фурье. Для построения графика, характеризующего сравнение точности обеих методов, составим следующий листинг программы:
Сравнительный анализ методов обратного преобразования Лапласа и Фурье# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import quad
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
tt = np.arange(0,100,0.01)
T1=25;T2=21;T3=12;K=0.37;tau=14
def invertfure(w,t):
j=(-1)**0.5
return (2/np.pi)*((K*np.exp(-tau*j*w)/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))).real*(np.sin(w*t)/w))
z=np.array([quad(lambda w: invertfure(w,t),0, 0.6)[0] for t in tt])
def h(t):
if t<=tau:
g=0
else:
g=(-K*(T1**2)*np.exp((tau-t)/T1)/((T1-T3)*(T1-T2)))+(K*(T2**2)*np.exp((tau-t)/T2)/((T1-T2)*(T2-T3)))+(-K*(T3**2)*np.exp((tau-t)/T3)/((T1-T3)*(T2-T3)))+K
return g
q=np.array([h(t) for t in tt])
from mpmath import *
mp.dps = 5; mp.pretty = True
def run_invertlaplace(tt,fp,tau):
y=[]
for i in np.arange(0,len(tt)):
if tt[i]<=tau:
y.append(0)
else:
y.append(invertlaplace(fp,tt[i],method='talbot'))
return y
fp = lambda p: K*exp(-tau*p)/((T1*p+1)*(T2*p+1)*(T3*p+1)*p)
y=np.array(run_invertlaplace(tt,fp,tau))
plt.title('Сравнительная оценка точности обратных \n Лапласа и Фурье преобразований ')
plt.plot(tt,q-y,'b',linewidth=2, label= 'Точное значение минус обратное преобразование Лапласа')
plt.plot(tt,q-z,'r',linewidth=2, label='Точное значение минус обратное преобразование Фурье')
plt.legend(loc='best')
plt.grid(True)
plt.show()
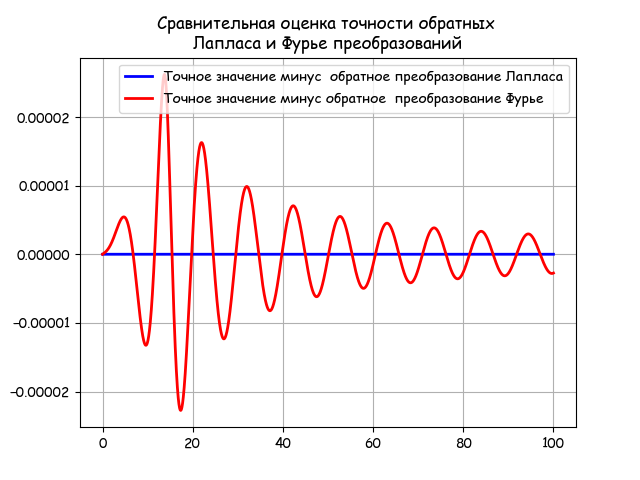
Из графика следует, что численное обратное преобразование Лапласа является более стабильным, чем Фурье и, кроме этого, оно совпадает с точным решением.
Выводы
1. Проведен сравнительный анализ численных методов обратного преобразования Лапласа и Фурье, показана большая точность и стабильность обратного преобразования Лапласа.
2. Показаны возможности применения библиотеки mpmath Python для обратного преобразования Лапласа основных передаточных функций объектов и элементов САУ.
Ссылки
- Расчёт и моделирование автоматических систем регулирования в среде Mathcad.
- Fredrik Johansson.
- Numerical inverse Laplace transform.