news.shamcode.ru | Использование нейронных сетей для распознавания рукописных цифр Часть 1

Использование нейронных сетей для распознавания рукописных цифр Часть 1

вторник, 18 июля 2017 г. в 03:13:30

Машинное обучение
Математика
Python

Привет, Хабр! В этой серии статей приведу краткий перевод с английского языка первой главы книги Майкла Нильсона "Neural Networks and Deep Learning".

Перевод я разбил на несколько статей на хабре, чтобы было удобнее читать:
Часть 1) Введение в нейронные сети
Часть 2) Построение и градиентный спуск
Часть 3) Реализация сети для распознавания цифр
Часть 4) Немного о глубоком обучении

Введение

Человеческая визуальная система — одна из самых удивительных на свете. В каждом полушарии нашего мозга есть зрительная кора, содержащая 140 млн. нейронов с десятками млрд. связей между ними, но такая кора не одна, их несколько, и вместе они образуют настоящий суперкомпьютер в нашей голове, лучшим образом адаптированный в ходе эволюции под восприятие визуальной составляющей нашего мира. Но трудность распознавания визуальных образов становится очевидной, если вы попытаетесь написать программу для распознавания, скажем, рукописных цифр.

Простую интуицию — "у 9-тки есть петля сверху, и вертикальный хвост внизу" не так просто реализовать алгоритмически. Нейронные сети используют примеры, выводят некоторые правила и учатся на них. Более того чем больше примеров мы покажем сети, тем больше она узнает о рукописных цифрах, следовательно классифицирует их с большей точностью. Мы напишем программу в 74 строчки кода, которая будет определять рукописные цифры с точностью >99%. Итак, поехали!

Персептрон

Что такое нейронная сеть? Для начала объясню модель искусственного нейрона. Персептрон был разработан в 1950 г. Фрэнком Розенблатом, и сегодня мы будем использовать одну из основных его моделей — сигмоидный персептрон. Итак, как он работает? Персепрон принимает на вход вектор $\bar{x} = \left \{ x_{1}, x_{2}, x_{3}, ..., x_{N} \right \}, x_{i} \in \mathbb{R}$ и возвращает некоторое выходное значение $output \in \mathbb{R}$ .

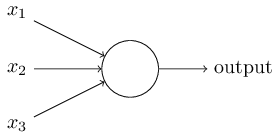
Розенблат предложил простое правило для вычисления выходного значения. Он ввел понятие "значимости", далее "веса" каждого входного значения $\bar{w} = \left \{ w_{1}, w_{2}, w_{3}, ..., w_{N} \right \}, w_{i} \in \mathbb{R}$ . В нашем случае $inline$ будет зависеть от того, будет ли $\sum_{i=1}^{N} x_{i}w_{i}$ больше или меньше некоторого порогового значения $threshold \in \mathbb{R}$ .

$output = \begin{cases} 0 & \text{ if } \sum_{i=1}^{N} x_{i}w_{i} \leq threshold \\ 1 & \text{ if } \sum_{i=1}^{N} x_{i}w_{i} > threshold \end{cases}$

И это все, что нам нужно! Варьируя $inline$ и вектор весов $\bar{w}$ , можно получить совершенно разные модели принятия решения. Теперь вернемся к нейронной сети.

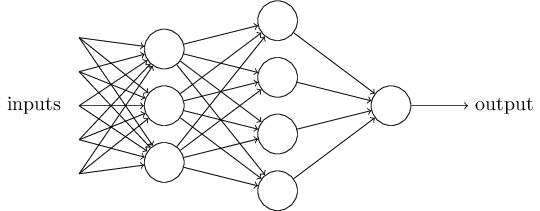
Итак, мы видим, что сеть состоит из нескольких слоев нейронов. Первый слой называется входным слоем или рецепторами ( $inline$ ), следующий слой — скрытый ( $inline$ ), и последний — выходной слой ( $inline$ ). Условие $\sum_{i=1}^{N} x_{i}w_{i} > threshold$ довольно громоздко, давайте заменим $\sum_{i=1}^{N} x_{i}w_{i}$ на скалярное произведение векторов $\bar{x} \cdot \bar{w}$ . Далее положим $inline$ , назовем его смещением персептрона или $inline$ и перенесем $inline$ в левую часть. Получим:

$output = \begin{cases} 0 & \text{ if } \bar{x} \cdot \bar{w} + b \leq 0 \\ 1 & \text{ if } \bar{x} \cdot \bar{w} + b > 0 \end{cases}$

Проблема обучения

Чтобы узнать, как может работать обучение, предположим что мы немного изменили некоторый вес или смещение в сети. Мы хотим, чтобы это небольшое изменение веса вызывало небольшое соответствующее изменение на выходе из сети. Схематически это выглядит так:

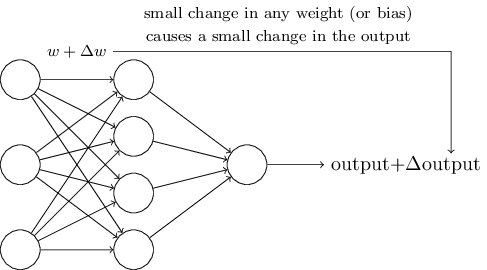
Если бы это было возможно, то мы могли бы манипулировать весами в выгодную нам сторону и постепенно обучать сеть, но проблема состоит в том, что при некотором изменение веса конкретного нейрона — его выход может полностью "перевернуться" с 0 на 1. Это может привести к большой ошибке прогноза всей сети, но есть способ обойти эту проблему.

Сигмоидный нейрон

Мы можем преодолеть эту проблему, введя новый тип искусственного нейрона, называемый сигмоидным нейроном. Сигмоидные нейроны подобны персептронам, но модифицированы так, что небольшие изменения в их весах и смещении вызывают лишь небольшое изменение на их выходе. Структура сигмоидного нейрона аналогичная, но теперь на вход он может принимать $0 \leq x_{i} \leq 1,\forall x_{i} \in \bar{x}$ , а на выходе выдавать $\sigma(\bar{x} \cdot \bar{w} + b)$ , где

$\begin{eqnarray} \sigma(z) = \frac{1}{1+e^{-z}}. \end{eqnarray}$

Казалось бы, совершенно разные случаи, но я вас уверяю, что персептрон и сигмоидный нейрон имеют много общего. Допустим, что $z = \bar{x} \cdot \bar{w} + b \rightarrow \infty$ , тогда $e^{-z} \rightarrow 0$ и, следовательно $\sigma(z) \rightarrow 1$ . Верно и обратное, если $z = \bar{x} \cdot \bar{w} + b \rightarrow -\infty$ , то $e^{-z} \rightarrow \infty$ и $\sigma(z) \rightarrow 0$ . Очевидно, что работая с сигмоидным нейроном мы имеем более сглаженный персептрон. И действительно:

$\Delta output \approx \sum_{i=1}^{N}\frac{\partial output}{\partial w_{i}} \Delta w_{i} + \frac{\partial output}{\partial b} \Delta b$

Архитектура нейронных сетей

Проектирование входных и выходных слоев нейросети — достаточно просто занятие. Для примера, предположим, что мы пытаемся определить, изображена ли рукописная "9" на изображении или нет. Естественным способом проектирования сети является кодирование интенсивностей пикселей изображения во входные нейроны. Если изображение имеет размер $64 \cdot 64$ , то мы имеем $4,096 = 64 \cdot 64$ входных нейрона. Выходной слой имеет один нейрон, который содержит выходное значение, если оно больше, чем 0.5, то на изображении "9", иначе нет. В то время как проектирование входных и выходных слоев — достаточно простая задача, выбор архитектуры скрытых слоев — искусство. Исследователи разработали множество эвристик проектирования скрытых слоев, например такие, которые помогают скомпенсировать количество скрытых слоев против времени обучения сети.

До сих пор мы использовали нейронные сети, в которых выход из одного слоя — использовался как сигнал для следующего, такие сети называются прямыми нейронными сетями или сетями прямого распространения( $inline$ ). Однако существуют и другие модели нейронных сетей, в которых возможны петли обратной связи. Эти модели называются рекуррентными нейронными сетями( $inline$ ). Рекуррентные нейронные сети были менее влиятельными, чем сети с прямой связью, отчасти потому, что алгоритмы обучения для рекуррентных сетей (по крайней мере на сегодняшний день) менее эффективны. Но рекуррентные сети по-прежнему чрезвычайно интересны. Они гораздо ближе по духу к тому, как работает наш мозг, чем сети с прямой связью. И вполне возможно, что повторяющиеся сети могут решать важные проблемы, которые могут быть решены с большим трудом с помощью сетей прямого доступа.

Итак, на сегодня все, в следующей статье я расскажу о градиентом спуске и обучении нашей будущей сети. Спасибо за внимание!