Мое основное увлечение - это аэрокосмос. И "космические" задачи - выведение полезных грузов на орбиту, возврат с орбиты через атмосферу являются функциями от целого набора параметров. К примеру, управление РН на первой ступени даже в двухмерной (без учета изменения азимута и dog-leg маневра)описывается по меньшей мере через 5 переменных:

• продолжительность вертикального участка набора высоты после старта;

• угол атаки при начале гравитационного разворота;

• продолжительность маневра заклонения;

• угол атаки после выполнения гравитационного разворота;

• длительности пауз между отсечкой двигателей первой ступени, отделением второй ступени и запуском двигателей второй ступени.

Еще можно добавить сюда дросселирование двигателей, ограничения по скоростному напору, требования по запасу топлива для возврата и посадки первой ступени.

Так что даже в самой простой постановке нужно рассматривать вектор из 10-15 компонентов (не забываем, есть еще 2-ья и 3-ья ступень, поля падения отработавших ступеней и обтекателей и еще много интересного). Аналитически через набор готовых формул такую задачу не решить. Нужны численные методы, среди которых известны, просты и понятны методы градиентного поиска. (я знаю про методы случайного поиска, генетические алгоритмы и swarm-методы, но мне нужно прозрачное, быстрое, грязное и надежное решение, которое не будет пытаться стать умнее меня)

Градие́нт (от лат gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины.

Осталось только найти величину шага, по которому мы будем продвигаться в направлении градиента вдоль каждого измерения. Постоянный шаг - простое и понятное решение, но разные переменные оказывают разное влияние на целевую функцию, и при постоянном шаге велика вероятность начать блуждание вдоль склонов "хребта" из локальных оптимумов.

Для поиска оптимального шага воспользуемся методом дихотомии. Простой, не требующий даже вычисления производных.

Объединим эти два метода, на каждом шаге сначала вычислим градиент, затем найдем оптимальные величины шага для каждой компоненты вектора аргументов целевой функции, затем перейдем в следующую точку, и если модуль разности значения целевой функции в этой точке и ранее полученного максимального значения окажется меньше достаточно малого эпсилона, то мы закончим поиск.

А чтобы не вывихнуть свой мозг сразу, начнем с простой и проверяемой задачи квадратичной регрессии. Суть проста - есть набор экспериментальных данных, описывающих зависимость некоего Y от параметра X (набор зашумлен и замусорен).

Надо найти такие коэффициенты a0, a1 и a2 для параболической функции, чтобы эта функция-аппроксимация, пропущенная через экспериментальный набор точек, имела бы наименьшее среднее отклонение между квадратичной аппроксимацией и экспериментальными данными. Такая задача была многократно решена самыми разными способами, и эти решения уже давно встроены в Excel, openOffice, MathCAD.

Поставим задачу: для фиксированной набора данных вида [X, Y] найти значения коэффициентов регрессии a0, a1, a2, чтобы сумма для всех X из нашей выборки |R(a0, a1, a2, X) - Y| была минимальна.

Начнем движение из точки [-5, -5, -5] (это не самая лучшая точка, и в идеале поиск стартовой точки должен решаться отдельно, но старт из субоптимальный условий - хорошая проверка расчетной схемы на устойчивость).

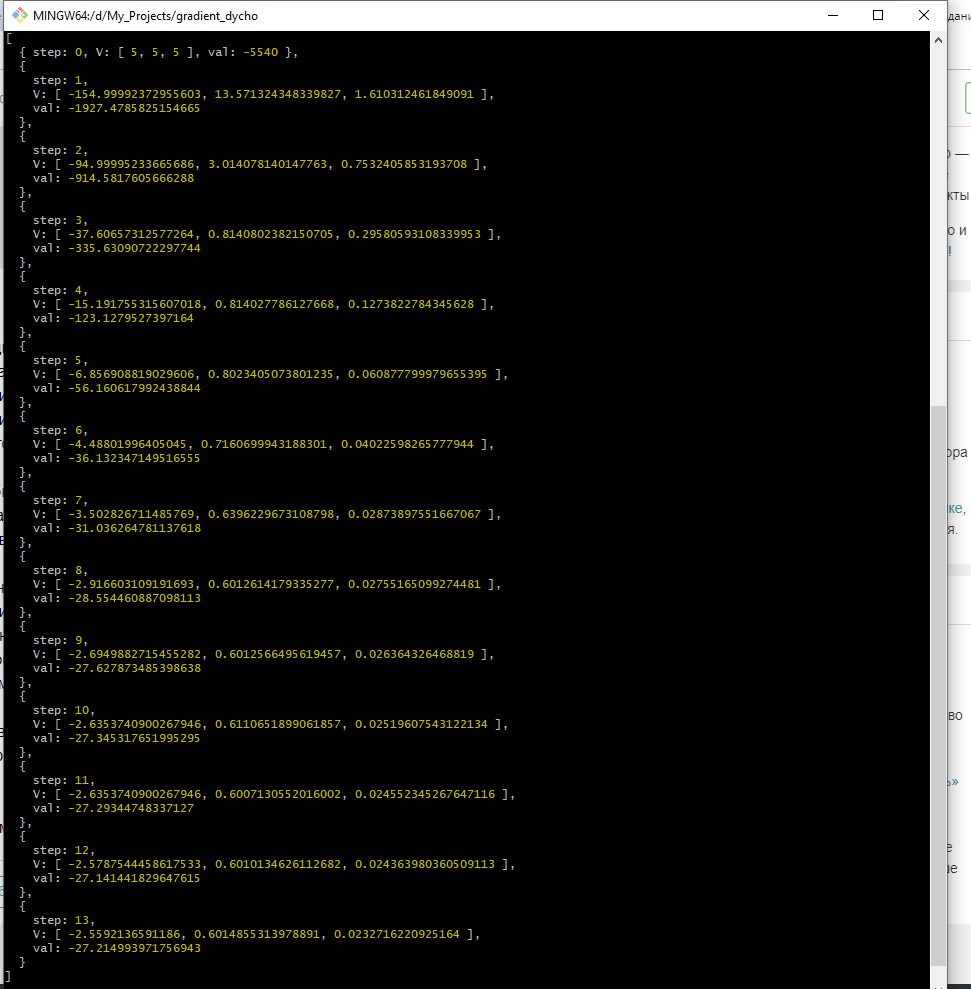
Теперь сравним полученные результаты с квадратичной регрессией, встроенной в openOffice.

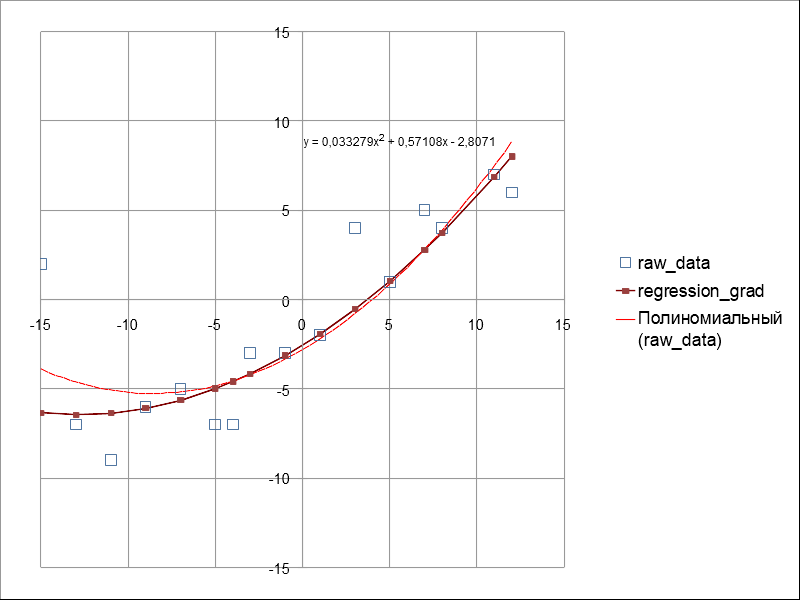
Теперь сравним количественные характеристики.

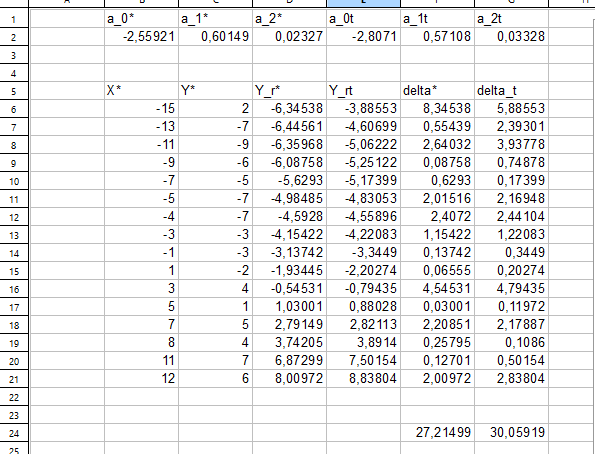
Выводы:

Градиентный поиск с подбором длины шага методом дихотомии действительно может находить максимум функции от вектора произвольной размерности.

Работоспособность метода подтверждена на задаче поиска коэффициентов квадратичной регрессии, в качестве эталона использовалась встроенная в openOffice planmaker функция полиноминальной регрессии.

Когда-нибудь я прикручу этот градиентный движок к своему рокетсайенсу.

Исходники алгоритма живут на моем гитхабе