В феврале 2025 года разработчики Go выпустили версию 1.24, в которой значительно улучшили производительность языка. Одно из ключевых изменений коснулось структуры map — встроенного типа данных, предназначенного для хранения и быстрого поиска значений по уникальному ключу. Новая реализация повысила эффективность работы map, оптимизировала использование памяти и ускорила операции поиска, вставки и удаления элементов. 

Привет, Хабр. Мы backend-разработчики SimbirSoft Павел и Алексей. В этой статье подробно разберём, как именно изменился механизм работы map и какие преимущества это даёт.

Основа — Swiss Table

В версии Go 1.24 реализация встроенного типа map была полностью переработана на основе структуры данных под названием Swiss Table. Эта структура, изначально разработанная инженерами Google для библиотеки Abseil, является высокопроизводительной хеш-таблицей, спроектированной для эффективной работы с кэш-памятью и быстрого доступа к данным.

Проблемы предыдущей реализации map

Ранее в Go для разрешения коллизий в хеш-таблицах использовался метод цепочек, при котором каждый бакет содержал указатель на связанный список элементов с одинаковым хеш-значением. Этот подход был рабочим, но не был лишён некоторых недостатков:

• Низкая локальность данных: элементы, связанные с одним и тем же хеш-значением, могли находиться в разных участках памяти, что приводило к частым промахам кэша и снижению производительности.

• Увеличение накладных расходов: использование указателей и связных списков увеличивало объём памяти, необходимый для хранения структуры данных.

• Ухудшение производительности: в случае большого числа коллизий возникало снижение производительности вследствие того, что приходилось последовательно проверять все элементы в цепочке элементов с одинаковым хеш-значением.

Как Swiss Table решает эти проблемы

Swiss Table использует несколько ключевых подходов, которые позволяют повысить производительность и разобраться со старыми проблемами.

Рассмотрим ключевые особенности Swiss Table:

• Открытая адресация: вместо использования связных списков для разрешения коллизий, как в методе цепочек, Swiss Table применяет открытую адресацию. Это означает, что все элементы хранятся непосредственно в одном массиве, что улучшает локальность данных и эффективность кэширования. Следовательно, при доступе к элементам map повышается вероятность того, что необходимые данные уже находятся в кэше процессора, что в свою очередь ускоряет операции поиска и вставки и соответственно снижает количество промахов кэша.

• Линейное пробирование с улучшениями: при возникновении коллизий оно используется с определёнными оптимизациями, что позволяет эффективно находить свободные слоты для новых элементов и уменьшает вероятность кластеризации.

• Группировка по 8 слотов (Group): таблица разделена на группы, каждая из которых содержит 8 слотов для пар «ключ-значение». Такой подход позволяет одновременно проверять несколько элементов, используя SIMD-оптимизации.

• Метаданные для слотов и контрольные слова (Control Word): каждая группа сопровождается 64-битным контрольным словом, которое содержит информацию о состоянии слотов. Каждый байт этого слова представляет собой один слот и содержит информацию о его занятости (свободен, занят или удалён). Также в контрольном слове хранится часть хеш-значения ключа, что ускоряет фильтрацию неподходящих слотов при поиске.

Чтобы облегчить дальнейшее восприятие описанных механизмов и структур, рассмотрим основные понятия, используемые в данной статье.

Основные понятия и термины Swiss Table

Группа

Группа — это логическая единица внутри Swiss Table, состоящая из 8 слотов для хранения пар «ключ-значение». Группа организована таким образом, чтобы все элементы в группе находились рядом в памяти. Это важное улучшение по сравнению с традиционными подходами, так как такая структура повышает локальность данных. Когда элементы группы располагаются в одном участке памяти, процессор с большей вероятностью будет находить их в своём кэше при обращении, что значительно уменьшает количество промахов кэша. В результате, операции поиска и вставки становятся быстрее.

Слоты внутри группы эффективно используют доступное пространство и минимизируют накладные расходы на управление памятью. В Swiss Table группы организуются таким образом, чтобы эффективно работать с современными архитектурами процессоров, используя SIMD-оптимизации, что позволяет ускорить обработку данных, обрабатывая сразу несколько элементов одновременно.

SIMD-оптимизация

SIMD-оптимизация (Single Instruction, Multiple Data) — это метод ускорения вычислений, при котором одна инструкция процессора применяется сразу к нескольким данным одновременно. В контексте Swiss Table этот подход используется для ускоренного поиска внутри группы из 8 слотов: благодаря применению SIMD-регистров процессор может за одно действие сравнивать контрольные байты всех слотов с искомым значением, тем самым значительно сокращая время поиска ключа в хеш-таблице.

• Параллелизм на уровне данных: вместо последовательной обработки каждого элемента данных по отдельности, SIMD позволяет выполнять одну инструкцию одновременно на группе элементов. Например, если у вас есть массив чисел, вы можете суммировать несколько пар чисел за одну инструкцию, используя SIMD-регистры, содержащие несколько значений одновременно. 

• Векторизация: данные группируются в векторные регистры фиксированного размера (например, 128, 256 или 512 бит). В таких регистрах могут размещаться несколько числовых значений (например, четыре 32-битных числа или восемь 16-битных чисел). Процесс преобразования стандартного кода для использования векторных инструкций называется векторизацией.

• Архитектурная поддержка: современные процессоры содержат специализированные векторные регистры и инструкции для работы по принципу SIMD. Эти инструкции позволяют выполнять операции над всеми элементами регистра одновременно.

Контрольное слово (Control Word)

Контрольное слово (Control Word) — это 8 байтовая структура, которая отвечает за быстрый поиск элементов в Swiss Table. Каждому из 8 слотов в группе соответствует 1 байт в контрольном слове.

Структура контрольного байта (Control Byte)

Каждый байт содержит два типа информации:

• 1 бит (старший) — флаг занятости (Empty / Deleted / Used), который указывает текущее состояние слота:

  • 0b00000000 (0x00) → Слот пуст (Empty)

  • 0b1xxxxxxx (H2) → Слот занят (Used)

  • 0b10000000 (0x80) → Слот удалён (Deleted) также данное состояние называют Tombstone, по своей сути является маркером для алгоритма пробирования, далее будет более подробно раскрыт смысл данного статуса.

• 7 бит (младшие) — нижние 7 бит из результата хеширования (H), в случае состояния Used.

H1 и H2

Здесь мы впервые сталкиваемся с таким понятием, как H. Отметим, что ранее в статье мы не говорили про H1 для групп, однако H1 тесно связано с группой и фигурирует в алгоритме поиска, который рассмотрим отдельным пунктом более подробно. Сейчас же для базового понимания рассмотрим более простое определение.

Допустим, у нас есть 64-битный хеш:
H = 1101010100110110001010111001010110100111100000001100010110010001 

в таком случае 

H1 (57 бит) → первые 57 бит, которые указывают на группу

H1 = 110101010011011000101011100101011010011110000000110001011

H2 (7 бит) → последние 7 бит, которые будут записаны в контрольное слово

H2 = 0010001

На данном этапе может возникнуть вопрос. А что же произойдёт в случае если H2 от хеш-функции будет равен H2 = 0000000? На данный случай распространяется специальное правило, если H2 будет равен 0, то вместо него в контрольное слово будет записано 0b0000001, это позволит избежать конфликта с пометкой контрольного байта в контрольном слове, как удалённого 0b10000000. Поскольку H2 это всё равно всего 7 бит, то вероятность, что такое изменение приведёт к коллизии, крайне мала, но таким образом гарантированно исключается случай с ложной пометкой состоянием Deleted.

Слот

Слот — это базовая ячейка хранения данных внутри Swiss Table. Каждый слот принадлежит определённой группе и включает в себя:

• Ключ (Key) хранит уникальный идентификатор элемента.

• Значение (Value) - данные, ассоциированные с ключом.

• Контрольный байт (Control Byte) — 1 байт в составе контрольного слова группы, указывающий на состояние слота. Важно, каждый слот не содержит физически контрольного байта внутри себя, но связан с ним через контрольное слово группы.

Мы рассмотрели ключевые структуры и механизмы Swiss Table, которые лежат в основе новой реализации map в Go 1.24. Теперь рассмотрим, как они работают на практике: как происходит вставка, поиск и удаление элементов, а также каким образом таблица динамически растёт и перераспределяет данные.

Принципы работы новой Map

Логика базовых операций Map

Процесс вставки нового элемента в Swiss Table состоит из нескольких этапов:

Вычисление хеша ключа и разбиение на H1 и H2

Сначала вычисляется 64-битный хеш от ключа. Далее он делится на 2 части, данный процесс мы подробно рассматривали в терминологии.

Определение начальной группы

Группа выбирается с помощью операции побитового И:

Группа = H1 & (число_групп - 1)

Это работает, поскольку количество групп — это степень двойки и побитовая маска выбирает младшие биты H1.

Допустим: H = 1101010100110110001010111001010110100111100000001100010110010001 (64 бита) H1 = 110101010011011000101011100101011010011110000000110001011

Группа = H1 & (8 - 1) = H1 & 0b111

Группа = 011 (3 в десятичной)

Поиск слота внутри группы

Как упоминалось ранее Swiss Table организована так, что каждая группа содержит 8 слотов.

• Поиск начинается с чтения контрольного слова и сравнения всех 8 байт с H2.

• Если слот имеет статус Deleted (tombstone), алгоритм продолжает пробирование, игнорируя его, а обнаружение пустого слота (Empty) означает, что в этой группе больше нет элементов, и поиск можно завершить.

• Если найден байт с таким же H2, то запускается процесс полного сравнения переданного ключа, с найденным ключом.

• В случае успешного сравнения возвращается соответствующее ключу значение.

• В случае неуспеха, возвращается значение по умолчанию для хранимого типа.

Для вставки элемента алгоритм поиска слота идентичен, но с некоторыми дополнениями:

• В случае успешного сравнения значение по соответствующему ключу переписывается на новое.

• Если найден слот в статусе Deleted (tombstone), алгоритм запоминает его как возможное место для вставки, но продолжает поиск, чтобы убедиться, что ключ отсутствует. Данный механизм пометки статусом Deleted служит для того, чтобы не прерывать цепочку пробирования. Если помечать удалённый слот, как Empty, то при поиске ключей алгоритм мог бы остановиться, решив, что дальше в цепочке нет элементов, и пропустить искомый элемент, который находится дальше в цепочке.

• Если найден слот в статусе Empty, то, если ранее был найден tombstone, используется tombstone — иначе элемент вставляется в найденный пустой слот.
  
  Допустим:

🔵 Empty (0x00) = свободное место

❌ Tombstone (0x80) = освободившийся слот, который нужно переиспользовать

✅ Used = занятые слоты

Последний слот пустой, вставка произойдёт в седьмой слот.

Третий слот содержит Tombstone, а седьмой слот пустой. В таком случае вставка произойдёт в третий слот с заглушкой.

Линейное пробирование, если группа заполнена

В том случае, если на первом шаге, где была определена начальная группа по формуле, она оказалась заполнена, то алгоритм не будет пересчитывать маску. Вместо этого он будет двигаться к следующей группе линейно, пока не найдёт свободный слот. Этот процесс повторяется до первой найденной группы с хотя бы одним свободным слотом.

Допустим:
У нас 8 групп и H1 & 0b111 дал группу 5, но она уже заполнена:

1. Группа 5 заполнена → идём к группе 6.

2. Группа 6 заполнена → идём к группе 7.

3. Группа 7 свободная → записываем туда.

В том случае, если заполнено слишком много слотов, а именно общий load factor таблицы превышает порог в 81,25%, то запускается расширение таблицы.

Рост таблицы

Вместо резкого увеличения размера хеш-таблицы используется extendible hashing, который позволяет расширять таблицу постепенно. Этот метод снижает накладные расходы при росте таблицы и минимизирует перераспределение элементов.

Директория (Directory)

Директория — это структура, управляющая ссылками на группы хеш-таблицы.

Директория минимизирует перераспределение элементов при расширении, используя механизм локальных и глобальных разделений (split и directory doubling). Она поддерживает масштабируемость структуры, позволяя таблице динамически расти без излишних накладных расходов.

На начальных этапах, когда общее число групп не превышает 1024, директория напрямую указывает на отдельные группы, используя младшие биты хеша для быстрого доступа. Такой подход обеспечивает эффективное распределение элементов и минимальные накладные расходы.

Однако, по мере роста таблицы, когда число групп превышает 1024, подход с монолитной таблицей становится неэффективным. В этот момент Swiss Table переходит к концепции подтаблиц. Вместо одной общей таблицы создаются независимые подтаблицы, каждая из которых содержит фиксированное число групп. Процесс адресации теперь разбивается на два этапа:

• Выбор подтаблицы: для этого используются старшие биты хеша, которые определяют, в какую подтаблицу попадет элемент.

• Выбор группы внутри подтаблицы: затем младшие биты используются для выбора конкретной группы в выбранной подтаблице.

Такой подход позволяет Swiss Table динамически изменять глубину адресации и масштабироваться, минимизируя перераспределение элементов и накладные расходы.

Увеличение таблицы при заполнении

Как говорилось выше, существует 2 типа разделения:

• split — локальное разделение на уровне переполнения групп, при данном разделении будет заранее аллоцирована подгруппа B, но на неё не будет ссылок до момента наступления directory doubling.

• directory doubling — удвоение количества групп в таблице происходит при достижении общей загрузки таблицы (load factor) в 81,25%, при этом локально перегруженные группы уже заранее аллоцировали себе память на подгруппы B на этапе split и на данном этапе они получают полноценные ссылки в директории.

Также существует особый случай расширения. При достижении 1024 групп, обычно это соответствует ~8192 элементам, таблица перестаёт быть монолитной. Вместо одной большой таблицы создаются независимые подтаблицы, каждая из которых продолжает расти отдельно.

Механизм выбора группы:

1. до 1024 групп: описан в разделе «Определение начальной группы»

2. после 1024 групп:

• директория указывает не на отдельные группы, а на подтаблицы;

• старшие биты хеш-значения используются для выбора подтаблицы;

• младшие биты используются для выбора конкретной группы внутри выбранной подтаблицы

Допустим:

У нас есть 2048 групп (2 подтаблицы по 1024 группы каждая)

Элемент с хешем: 

H1(A) = 0b011011001011011000101011100101011010011110000000110001011

1. Первый бит 0b0 → указывает на первую подтаблицу

2. Поскольку каждая подтаблица содержит 1024 группы (2¹⁰), для выбора группы внутри подтаблицы используются 10 следующих бит.
   Соответственно следующие 10 бит 0b1101100101→ указывают на группу внутри подтаблицы.

Перемещение элементов

Элементы не просто копируются в новую таблицу, а перераспределяются в соответствии с новыми битами хеша. Например, если изначально использовалось N бит хеша для определения группы, то после расширения может использоваться N+1 бит. Это происходит потому, что при увеличении числа групп их количество удваивается, а значит, для их адресации требуется еще один дополнительный бит хеша.

В случае, если хеш-таблица разделена на несколько подтаблиц, процесс выбора элемента проходит в два этапа: сначала с помощью старших бит хеша определяется, в какую подтаблицу попадет элемент, а затем младшие биты используются для выбора конкретной группы внутри выбранной подтаблицы.

Например:

у нас есть 8 групп, как в примерах ранее, и мы используем 3 бита хеша по маске для выбора группы. Пусть есть хеш значения для двух ключей:

H1(A) = 0b011011001011011000101011100101011010011110000000110001011

H1(B) = 0b111011001011011000101011100101011010011110000000110001011

При текущем размере таблицы 8 групп используется 3 бита:

A: H1(A) & 0b111 = 0b011 → Группа 3

B: H1(B) & 0b111 = 0b011 → Группа 3

При увеличении размера таблицы до 16 групп используется 4 бита:

A: H1(A) & 0b1111 = 0b0011 → Группа 3 (остался)

B: H1(B) & 0b1111 = 0b1011 → Группа 11 (переместился)

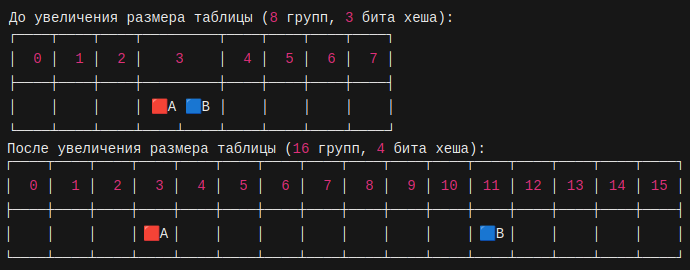
На данном примере наглядно видно, что произошло разделение группы, а не полное перемещение всех элементов.

Подведем итог

Подытожим механизмы борьбы с коллизиями новой реализации map в Go 1.24, основанной на Swiss Table:

• Быстрое отсеивание позволяет отбрасывать неподходящие слоты без обращения к ключам.

• Полное сравнение ключей гарантирует корректное разрешение коллизий при совпадении H2.

• Использование tombstone позволяет сохранять непрерывность пробирования при удалении элементов.

• Линейное пробирование минимизирует количество перехеширований и равномерно распределяет нагрузку.

Эти методы наряду с другими улучшениями делают map более эффективным и производительным:

• Улучшенная локальность данных — группировка слотов и контрольные слова сокращают количество кеш-промахов.

• Быстрый поиск — SIMD-оптимизации позволяют сравнивать сразу 8 кандидатов на соответствие.

• Гибкое расширение — постепенный рост через split и directory doubling, а также разделение на подтаблицы после 1024 групп снижает накладные расходы на перераспределение.

Новая архитектура map в Go 1.24 не только ускоряет поиск и вставку, но и делает структуру более устойчивой к коллизиям и масштабируемой, что критично для современных высоконагруженных систем.

Спасибо за внимание!

Больше авторских материалов для backend-разработчиков от моих коллег читайте в соцсетях SimbirSoft – ВКонтакте и Telegram.