https://habr.com/ru/post/439674/- Python
- Программирование
- Алгоритмы
- Машинное обучение
- Разработка робототехники
Это давно назревшая статья об обучении с подкреплением Reinforcement Learning (RL). RL – крутая тема!
Вы, возможно, знаете, что компьютеры теперь могут
автоматически учиться играть в игры ATARI (получая на вход сырые игровые пиксели!). Они бьют чемпионов мира в игру
Го, виртуальные четвероногие учатся
бегать и прыгать, а роботы учатся выполнять сложные задачи манипуляции, которые бросают вызов явному программированию. Оказывается, что все эти достижения не обходятся без RL. Я также заинтересовался RL в течение прошлого года: я работал с книгой
Ричарда Саттона (прим.пер.: ссылка заменена), читал курс
Дэвида Сильвера, смотрел
лекции Джона Шульмана, написал
библиотеку RL на Javascript, летом проходил практику в DeepMind, работая в группе DeepRL, и совсем недавно — в разработке
OpenAI Gym, – нового инструментария RL. Так что я, конечно, был на этой волне, по крайней мере, год, но до сих пор не удосужился написать заметку о том, почему RL имеет большое значение, о чем он, как все это развивается.
 Примеры использования Deep Q-Learning. Слева направо: нейросеть играет в ATARI, нейросеть играет в AlphaGo, робот складывает Лего, виртуальный четвероногий бегает по виртуальным препятствиям.
Примеры использования Deep Q-Learning. Слева направо: нейросеть играет в ATARI, нейросеть играет в AlphaGo, робот складывает Лего, виртуальный четвероногий бегает по виртуальным препятствиям.
Интересно поразмышлять о характере недавнего прогресса в RL. Мне хочется отметить четыре отдельных факторах, влияющих на развитие ИИ:
- Скорость вычислений (GPU, специальные устройства ASIC, закон Мура)
- Достаточное количество данных в пригодном виде (например, ImageNet)
- Алгоритмы (исследования и идеи, например, backprop, CNN, LSTM)
- Инфраструктура (Linux, TCP/IP, Git, ROS, PR2, AWS, AMT, TensorFlow и т. д.).
Так же, как и в компьютерном зрении, прогресс в RL движется, …хотя но не так сильно, как может показаться. Например, в компьютерном зрении нейросеть AlexNet 2012 является увеличенной в глубину и ширину версией нейросети ConvNets 1990-х годов. Точно так ATARI Deep Q-Learning 2013 года представляет собой реализацию стандартного алгоритма Q-Learning, который вы можете найти в классической книге Ричарда Саттона 1998 года. Далее, AlphaGo использует технику Policy Gradient и поиск по дереву Монте-Карло (MCTS) — это также старые идеи или их комбинации. Конечно, требуется много навыков и терпения, чтобы заставить их работать, и было разработано множество хитрых настроек поверх старых алгоритмов.
Но в первом приближении основным драйвером недавнего прогресса являются не новые алгоритмы и идеи, а – интенсификация вычислений, достаточные данные, зрелая инфраструктура.
Теперь вернемся к RL. Много людей не могут поверить, что мы можем научить компьютер играть в игры ATARI на человеческом уровне по сырым пикселями с нуля и используя один и тот же самообучающийся алгоритм. При этом всякий раз я ощущаю разрыв – каким оно кажется волшебным, и как просто оно устроено внутри на самом деле.
Основной подход, который мы используем, на самом деле довольно тупой. Как бы то ни было, я бы хотел познакомить вас с техникой Policy Gradient (PG), – нашим любимым выбором по умолчанию для решения проблем с RL на данный момент. Вам может быть любопытно, почему я вместо этого не представляю DQN, который является альтернативным и более известным алгоритмом RL, который тоже используется при
обучении ATARI. Оказывается, хоть Q-Learning известен, но не так уж идеален. Большинство людей предпочитают использовать Policy Gradient, включая авторов оригинальной
статьи по DQN, которые показали, что при хорошей настройке Policy Gradient работает даже лучше, чем Q-Learning. PG предпочтительнее, потому что он явный: есть четкая политика и внятный подход, который напрямую оптимизирует ожидаемое вознаграждение. В качестве примера мы научимся играть в ATARI Pong: с нуля, из сырых пикселей через Policy Gradient с нейронной сетью. И все это уложим в 130 строк Python. (
Gist link )Давайте разберем, как это делается.

 Выше: Пинг-Понг. Ниже: Представление Пинг-понга, как специальный случай марковского процесса принятия решений (MDP) : Каждая вершина графа соответствует определенному состоянию игры, а ребра определяют вероятности перехода в другие состояния. Каждое ребро так же определяет вознаграждение. Целью является нахождение оптимального пути из любого состояния чтобы максимизировать награду
Выше: Пинг-Понг. Ниже: Представление Пинг-понга, как специальный случай марковского процесса принятия решений (MDP) : Каждая вершина графа соответствует определенному состоянию игры, а ребра определяют вероятности перехода в другие состояния. Каждое ребро так же определяет вознаграждение. Целью является нахождение оптимального пути из любого состояния чтобы максимизировать награду
Игра в Пинг-Понг является отличным примером задачи RL. В версии ATARI 2600 мы будем играть одной ракеткой сами. Другая ракетка контролируется встроенным алгоритмом. Нам нужно отбивать мяч так, чтобы другой игрок не успел его отбить. Надеюсь, что нет необходимости объяснять, что такое Пинг-Понг. На низком уровне игра работает следующим образом: мы получаем кадр изображения — массив байтов 210x160x3, и решаем, – хотим ли мы перемещать ракетку ВВЕРХ или ВНИЗ. То есть имеем всего два выбора по управлению игрой. После каждого выбора игровой симулятор выполняет свое действие и дает нам вознаграждение: либо +1 вознаграждение, если мяч прошел мимо ракетки соперника, либо -1, если мы пропустили мяч. В противном случае 0. И, конечно же, наша цель состоит в том, чтобы перемещать ракетку, чтобы мы получили как можно большее вознаграждение.
При рассмотрении решения помните, что мы попытаемся сделать ооочень мало предположений о понге, потому что он сам по себе не особо важен на практике. Мы намного больше вещей учитываем в масштабных задачах, таких как манипуляции с роботами, сборка и навигация. Понг — это просто забавный игрушечный тестовый пример, с которым мы играем, пока разбираемся, как писать очень общие системы ИИ, которые однажды могут выполнять произвольные полезные задачи.
Нейросеть в качестве политики RL. Во-первых, мы собираемся определить так называемую политику, которая реализует наш игрок (или «агент»). ((*)«Агент», «среда» и «политика агента» — это стандарные термины из теории RL). Функция политики в нашем случае — это нейросеть. Она примет на вход состояние игры и на выходе решит, что нам делать – двигаться вверх или вниз. В качестве нашего любимого простого блока вычислений мы будем использовать двухслойную нейронную сеть, которая берет сырые пиксели изображения (всего 100 800 чисел (210 * 160 * 3)) и выдает одно число, указывающее вероятность двигать ракетку вверх. Обратите внимание, что использование стохастической политики является стандартным, что означает, что мы производим только вероятность движения вверх. Чтобы получить фактический ход мы будем использовать эту вероятность. Причина этого станет более понятной, когда мы поговорим о тренировках.
 Наша функция политики, состоящая из 2х слойной полносвязанной нейросети
Наша функция политики, состоящая из 2х слойной полносвязанной нейросети
Говоря конкретнее, предположим, что на вход мы полчаем векто Х, который содержит набор предобработанных пикселей. Тогда мы должны вычислить с помощью python\numpy:
h = np.dot(W1, x) # compute hidden layer neuron activations
h[h<0] = 0 # ReLU nonlinearity: threshold at zero
logp = np.dot(W2, h) # compute log probability of going up
p = 1.0 / (1.0 + np.exp(-logp)) # sigmoid function (gives probability of going up)
В этом фрагменте W1 и W2 – это две матрицы, которые мы инициализируем случайным образом. Мы не используем смещения (bias), потому что так захотелось. Обратите внимание, что в конце мы используем нелинейность сигмоида, которая сводит выходную вероятность к диапазону [0,1]. Интуитивно понятно, что нейроны в скрытом слое (веса которых расположены в W1) могут обнаруживать различные игровые сценарии (например, мяч находится сверху, а наша ракетка находится посередине), а веса в W2 могут затем решить, должны ли мы в каждом случае идти вверх или вниз. Начальные случайные W1 и W2, конечно, поначалу будут вызывать у нашего нейро-игрока спазмы и конвульсии, что приравнивает его к имбицилу-аутисту за штурвалом самолета. Так что единственной задачей сейчас является найти W1 и W2, которые ведут к хорошей игре!
Имеется замечание о предварительной обработке пикселей, – в идеале надо передать как минимум 2 кадра в нейросеть, чтобы она могла обнаруживать движение. Но чтобы упростить ситуацию, мы будем подавать разность двух кадров. То есть будем вычитать текущий и предыдущий кадры и только затем подавать разницу на вход нейросети.
Звучит как нечто невозможное. На этом этапе я бы хотел, чтобы вы оценили, насколько сложна проблема RL. Мы получаем 100 800 чисел (210х160х 3) и пересылаем в нашу нейросеть, реализующую политику игрока (которая, кстати, легко включает порядка миллиона параметров в матрицах W1 и W2). Предположим, что мы в какой-то момент решили пойти вверх. Симулятор игры может ответить, что на этот раз мы получим 0 наград и дадим нам еще 100 800 чисел для следующего кадра. Мы можем повторить этот процесс сотни раз, прежде чем получим ненулевое вознаграждение! Например, предположим, мы наконец получили награду +1. Это замечательно, но как тогда мы можем сказать, – что к этому привело? Было ли это то действие, что мы сделали только сейчас? Или, может быть, 76 кадров назад? Или, может быть, это было связано сначала с кадром 10, а затем мы что-то правильно сделали в кадре 90? И как мы выясним, – какую из миллиона «ручек» крутить, чтобы добиться еще большего успеха в будущем? Мы называем это задачей определения коэффициента доверия к тем или иным действиям. В конкретном случае с понгом мы знаем, что получаем +1, если мяч прошел мимо соперника. Истинная причина в том, что мы случайно пнули мяч по хорошей траектории несколько кадров назад, а каждое последующее действие, которое мы выполняли, никак не влияло. Другими словами, мы столкнулись с очень сложной вычислительной проблемой, и все выглядит довольно мрачно.
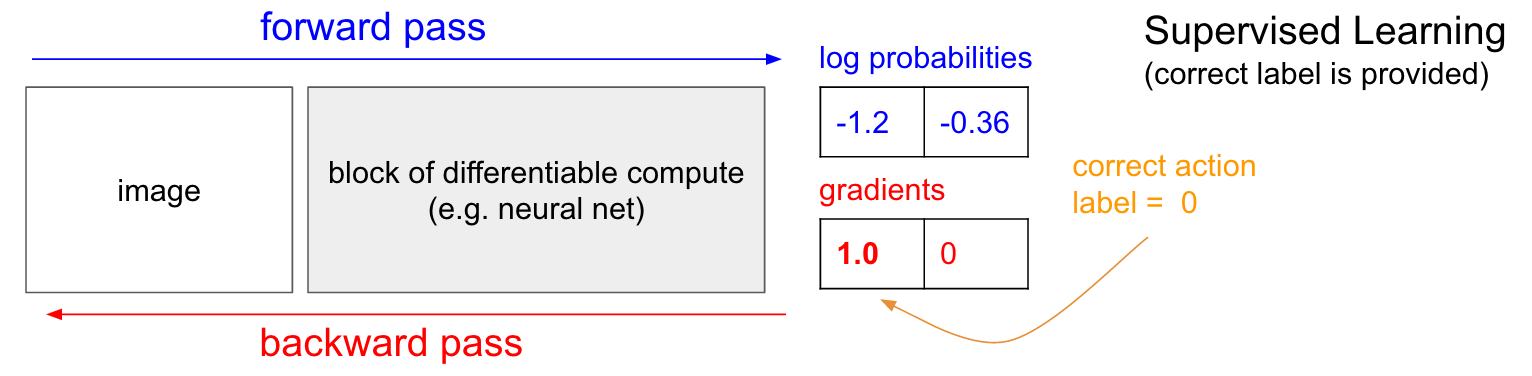
Обучение с учителем. Прежде чем мы углубимся в градиент политики (PG), я хотел бы кратко вспомнить про обучении c учителем, потому что, как мы увидим, RL очень похож. Обратитесь к диаграмме ниже. В обычном обучении с учителем мы будем передавать изображение в сеть и получать на выходе некоторые числовые вероятности для классов. Например, в нашем случае имеем два класса: ВВЕРХ и ВНИЗ. Я использую логарифмические вероятности (-1,2, -0,36) вместо вероятностей в формате 30% и 70%, потому что мы оптимизируем логарифмическую вероятность правильного класса (или метки). Это делает математические выкладки элегантнее и эквивалентно оптимизации просто вероятности, потому что логарифм является монотонным.
В обучении с учителем у нас будет мгновенный доступ к правильному классу (метке). На этапе обучения нам точно скажут, какой именно сейчас нужно сделать правильный шаг (допустим это ВВЕРХ, метка 0), хотя нейросеть возможно думает иначе. Поэтому вычисляем градиент
, чтобы подправить параметры сети. Этот градиент как раз и подсказывает, как мы должны изменить каждый из наших миллионов параметров, чтобы сеть немного с большей вероятностью предсказывала ВВЕРХ в такой же ситуации. Например, один из миллиона параметров в сети может иметь градиент -2.1, что означает, что если бы мы увеличили этот параметр на небольшую положительную величину (например, 0,001), то логарифмическая вероятность UP снизилась бы на 2,1 * 0,001. (уменьшение из-за отрицательного знака). Если мы применим градиент и затем обновим параметр с помощью алгоритма обратного распространения, то, да, наша сеть будет выдавать большую вероятность ВВЕРХ, когда увидит такое же или очень похожее изображение в будущем.
 Градиенты политики (PG)
Градиенты политики (PG). Хорошо, но что нам делать, если у нас нет правильной метки обучения подкреплению? Вот решение для PG (снова обратитесь к диаграмме ниже). Наша нейросеть рассчитала вероятность подъема на 30% (logprob -1.2) и ВНИЗ на 70% (logprob -0.36). Теперь мы делаем выборку из из этого распределения и конкретизируем какое именно действие сделаем; Например, выбрали ВНИЗ и послали это действие игровому симулятору. В этот момент обратите внимание на один интересный факт: мы могли бы сразу вычислить и применить градиент для действия ВНИЗ, как мы это делали в обучении с учителем, и тем самым побудить сеть с большей вероятностью выполнить действие ВНИЗ в будущем. Таким образом, мы можем сразу оценить и запомнить этот градиент. Но проблема в том, что на данный момент мы еще не знаем, – хорошо ли идти ВНИЗ? Но самое интересно то, мы можем просто немного подождать и применить его позже! В Понге мы могли подождать до конца игры, затем взять полученное вознаграждение (либо +1, если мы выиграли, либо -1, если мы проиграли), и ввести его в качестве множителя к градиенту. Так что, если мы введем -1 для вероятности ВНИЗ и сделаем обратное распростанение, то перестроим параметры сети, чтобы менее вероятно выполнять действие ВНИЗ будущем, когда встретит такую же картинку, так как принятие этого действия привело к тому, что мы проиграли игру. То есть нам надо будет как-то запомнить все действия (входы и выходы нейросети) в одном эпизоде игры и на основании этого массива подкрутить нейросеть почти так же, как и в обучении с учителем.
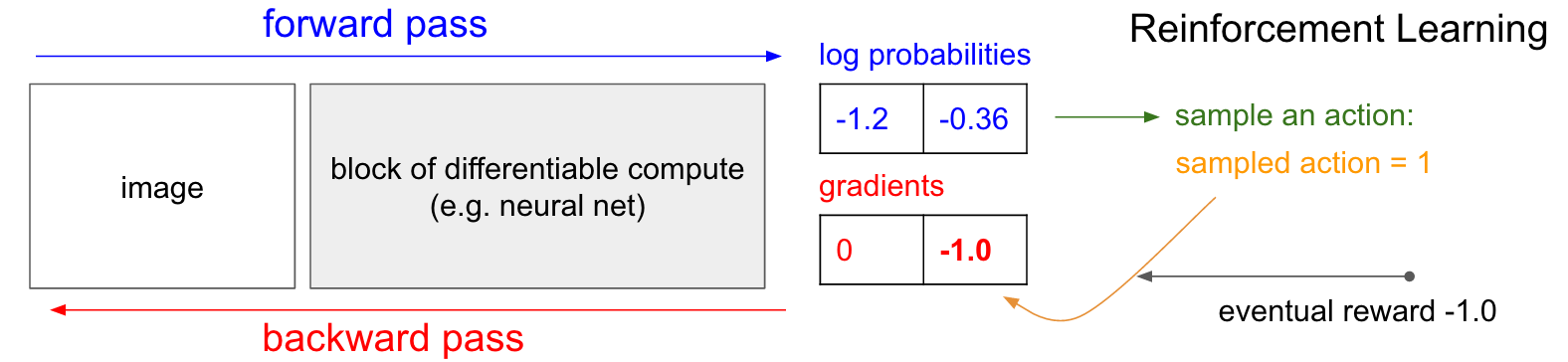
И это все, что надо: у нас есть стохастическая политика, которая выбирает действия, а затем в будущем поощряются действия, которые в конечном итоге приводят к хорошим результатам, а действия, которые приводят к плохим результатам, не поощряются. Кроме того, награда даже не должна быть +1 или -1, если мы в конечном итоге выиграем игру. Это может быть произвольная величина такого же смысла. Например, если все получится действительно хорошо, это может быть 10.0, который мы затем введем как градиент вместо -1, чтобы начать с обратное распространение backprop. В этом красота нейронных сетей. Их использование может показаться обманом: вам разрешено иметь 1 миллион параметров, встроенных в 1 терафлоп вычислений, и вы можете заставить его делать произвольные вещи со стохастическим градиентным спуском (SGD). Это не должно работать, но забавно, что мы живем во вселенной, где это работает.
Если бы мы играли в простые настольные игры, типа шашек, то порядок был бы примерно таким же. При этом есть заметное отличие от алгоритмов минимакса или алфа-бета отсечения. В этих алгоритмах программа заглядывает на несколько шагов вперед, зная правила игры и анализирует миллионы позиций. В подходе же RL анализируются только фактически сделанные ходы. При этом нейросеть не заглядывает вперёд, так как ничего не знает о правилах игры.
Порядок тренировки в деталях. Мы создаем и инициализируем нейросеть с некоторыми W1, W2 и сыграем в 100 игр понга (мы называем это «обкатка» политики). Предположим, что каждая игра состоит из 200 кадров, так что в общей сложности мы приняли 100*200 = 20 000 решений идти вверх или вниз. И для каждого из решений мы знаем градиент, который говорит нам, как должны изменится параметры, если мы хотим поощрять или запрещать это решение в этом состоянии в будущем. Все, что остается сейчас, — это маркировать каждое принятое нами решение как хорошее или плохое. Например, предположим, что мы выиграли 12 игр и проиграли 88. Мы примем все 200 * 12 = 2400 решений, которые мы приняли в играх-победителях, и сделаем положительное обновление (заполняя градиент +1.0 для каждого действия, выполняя backprop, и обновление параметров, поощряющее действия, которые мы выбрали во всех этих штатах). И мы примем другие 200 * 88 = 17600 решений, которые мы приняли в проигрышных играх, и сделаем негативное обновление (не одобряя того, что мы сделали). И это все, что надо. Сеть теперь станет с большей вероятностью повторять действия, которые сработали, и немного с меньшей вероятностью повторять действия, которые не сработали. Теперь мы играем еще 100 игр с нашей новой, немного улучшенной политикой, а затем повторяем применение градиентов.
 Мультипликационная схема из 4 игр. Каждый черный круг — это какое-то игровое состояние (три примера состояний показаны внизу), а каждая стрелка — это переход, помеченный действием, которое было выбрано. В этом случае мы выиграли 2 игры и проиграли 2 игры. Мы брали две выигранные нами игры и слегка поощряли каждое действие, которое мы сделали в этом эпизоде. И наоборот, мы также возьмем две проигранные игры и слегка отговорим от каждого отдельного действия, которое мы сделали в этом эпизоде.
Мультипликационная схема из 4 игр. Каждый черный круг — это какое-то игровое состояние (три примера состояний показаны внизу), а каждая стрелка — это переход, помеченный действием, которое было выбрано. В этом случае мы выиграли 2 игры и проиграли 2 игры. Мы брали две выигранные нами игры и слегка поощряли каждое действие, которое мы сделали в этом эпизоде. И наоборот, мы также возьмем две проигранные игры и слегка отговорим от каждого отдельного действия, которое мы сделали в этом эпизоде.
Если вы поразмышляете над этим, вы начнете находить несколько забавных свойств. Например, что если мы сделали хорошее действие в 50 кадре, правильно пиная мяч, но затем пропустили мяч в 150 кадре? Так как мы проиграли партию, то каждое отдельное действие теперь помечено как плохое, и разве это не помешает правильному удару на 50 кадре? Вы правы — так и будет для этой партии. Однако, когда вы рассматриваете процесс в тысячах / миллионах игр, то правильное выполнение отскока повышает вашу вероятность выиграть в будущем. В среднем вы увидите больше положительных, чем отрицательных обновлений для правильного удара ракеткой. И нейросеть, реализующая политику, будет в конечном итоге выдавать правильные реакции.
Обновление: 9 декабря 2016 г. — альтернативный взгляд. В своем объяснении выше я использую такие термины, как «определение градиента и обратное распространение backprop», что является определенным искусным приемом. Если вы привыкли писать собственный код обратного распространения backprop или используете Torch, когда вы можете полностью управлять градиентами. Однако, если вы привыкли к Theano или TensorFlow, вы будете немного озадачены, потому что код backprop полностью автоматизирован и его трудно настроить под себя. В этом случае следующий альтернативный взгляд может быть более продуктиным. В обучении с учителем обычная цель состоит в том, чтобы максимизировать
, где
— обучающие примеры (такие как изображения и их метки). Применение градиента к функции политики в точности совпадает с обучением с учителем, но с двумя небольшими отличиями: 1) у нас нет правильных меток
, поэтому в качестве «поддельной метки» мы используем действие, которое мы получили для выборки из политики, когда она увидела
, и 2 ) Мы вводим еще коэффициент целесообразности (advantage) для каждого действия. Таким образом, в итоге наша потеря теперь выглядит как
, где
— это действие, которое мы провели с выборкой, а
— это число, которое мы называем коэффициентом целесообразности. Например, в случае с понгом значение
может быть равно 1.0, если мы в конечном итоге выиграем в эпизоде, и -1.0, если мы проиграли. Это гарантирует, что мы максимизируем вероятность регистрации действий, которые привели к хорошему результату, и минимизируем вероятность регистрации тех действий, которые этого не сделали. А нейтральные действия в результате многих заходов не будут особо влиять на функцию политики. Таким образом, обучение с подкреплением точно такое же, как обучение с учителем, но на постоянно меняющемся наборе данных (эпизодах), с дополнительным коэффициентом.
Более продвинутые функции целесообразности. Я также обещал немного больше информации. До сих пор мы оценивали правильность каждого отдельного действия, основываясь на том, выиграем мы или нет. В более общей настройке RL мы будем получать «зависящее от условий вознаграждение»
за каждый шаг в зависимости от номера шага или времени. Одним из распространенных вариантов является использование дисконтированного коэффициента, поэтому «возможное вознаграждение» на приведенной выше диаграмме будет
, где
— это число от 0 до 1, называемое коэффициентом дисконтирования (например, 0,99). Выражение говорит, что сила, с которой мы поощряем действие, представляет собой взвешенную сумму всех наград, но последующие награды экспоненциально менее важны. На практике также бывает нужно их нормализовать. Например, предположим, что мы вычисляем
для всех 20 000 действий в серии из 100 эпизодов игры. Очень хорошая идея — нормализировать эти значения (вычесть среднее, разделить на стандартное отклонение), прежде чем мы подключим их к алгоритму backprop. Таким образом, мы всегда поощряем и препятствуем примерно половине выполненных действий. Это уменьшает флуктуации и делает политику более сходимой. Более глубокое исследование можно найти по [
ссылке].
Производная от функции политики. Я также хотел кратко рассказать, как градиенты берутся математически. Градиенты функции политики являются частным случаем более общей теории. Общий случай состоит в том, что когда у нас есть выражение вида
, то есть матожидание некоторой скалярной функции
при некотором распределении её параметра
, параметризованного некоторым вектором
.
станет нашей функцией вознаграждения (или функцией целесообразности в более общем смысле), а дискретное распределение
будет нашей политикой, которая на самом деле имеет вид
, давая вероятности того или иного действия a для картинки
. Затем нас интересует, как нам сместить распределение p через его параметры
, чтобы увеличить
(т.е. как мы изменим параметры сети, чтобы действия получили более высокое вознаграждение). У нас есть это:
Постараюсь объяснить это. У нас есть некоторое распределение
(я использовал сокращение
, из которого мы можем произвести выборку конкретных значений. Например, это может быть гауссово распределение, из которого генератор случайных чисел производит выборку. Для каждого примера мы также можем вычислить функцию оценки
, которая по текущему примеру дает нам некоторую скалярную оценку. Полученное уравнение говорит нам о том, как мы должны сдвинуть распределение через его параметры
, если мы хотим, чтобы дальнейшие примеры действий на его основе получали более высокие показатели
. Берем несколько примеров действий
и их оценки
, и также для каждого x также оцениваем второй член
. Что это за множитель? Это как раз и есть вектор — градиент, который дает нам направление в пространстве параметров, которое приведет к увеличению вероятности конкртетного действия
. Другими словами, если бы мы подтолкнули θ в направлении
, мы бы увидели, что новое вероятность этого действия немного возрастет. Если вы оглянетесь на формулу, она говорит нам о том, что мы должны взять это направление и умножить на него скалярное значение
. Это сделает так, что примеры действий с более высокой оценкой (в нaшем случае вознаграждением) будут «тянуть» сильнее, чем примеры с более низким показателем, поэтому, если бы мы делали обновление на основе нескольких выборок из
, плотность вероятности сместилась бы в направление более высоких результирующих баллов игры, что повышает вероятность получения примеров действий с высоким вознаграждением. Важно, что градиент не берется от функции
, так как она вообще может быть недифферинцируемой и непредсказуемой. А
дифференцируема по
. То есть
является плавно настраиваемым дискретным распределением, где можно регулировать вероятности отдельных действий. Так же будем считать, что
нормализовано.
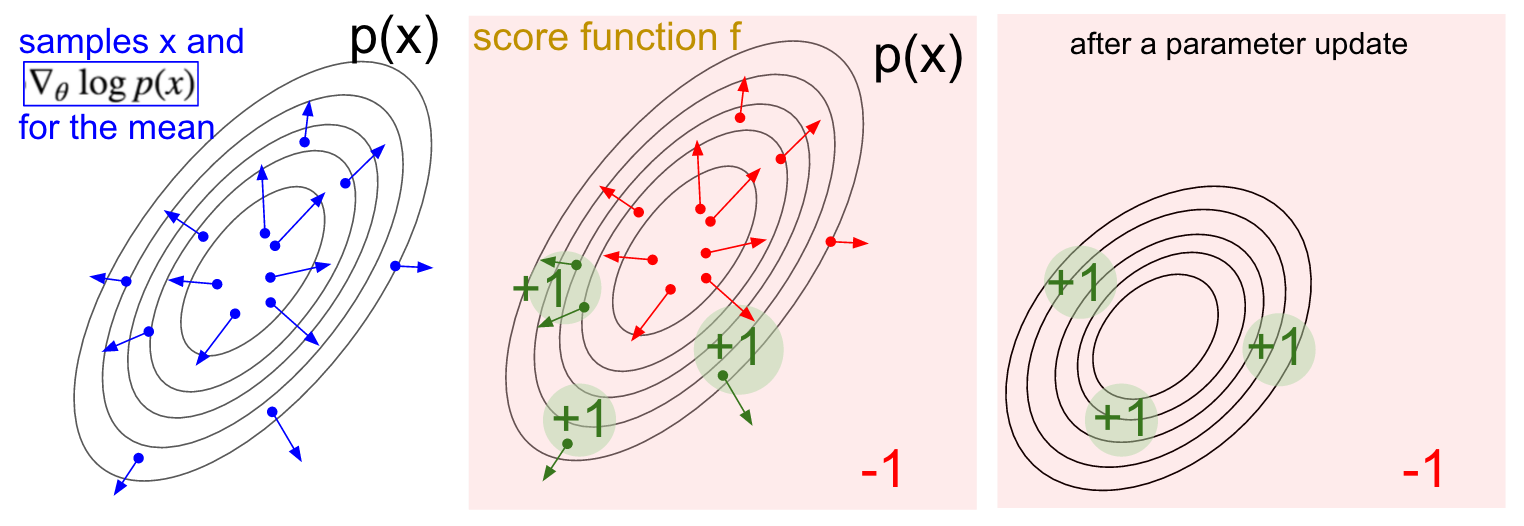 Визуализация градиента. Слева: Гауссово распределение и несколько примеров из него (синие точки). На каждой синей точке мы также наносим градиент логарифмической вероятности относительно среднего параметра. Стрелка указывает направление, в котором следует сместить среднее значение распределения, чтобы увеличить вероятность этого примера действий. В середине: Добавлена некоторой функции оценки, дающей -1 везде, кроме +1 в некоторых небольших регионах (обратите внимание, что это может быть произвольная и не обязательно дифференцируемая скалярная функция). Стрелки теперь имеют цветовую кодировку, потому что из-за умножения мы собираемся усреднить все зеленые стрелки с положителной оценкой и отрицательные красные стрелки. Справа: после обновления параметров зеленые стрелки и перевернутые красные стрелки подталкивают нас влево и вниз. Образцы из этого распределения теперь будут иметь более высокую ожидаемую оценку, по желанию.
Визуализация градиента. Слева: Гауссово распределение и несколько примеров из него (синие точки). На каждой синей точке мы также наносим градиент логарифмической вероятности относительно среднего параметра. Стрелка указывает направление, в котором следует сместить среднее значение распределения, чтобы увеличить вероятность этого примера действий. В середине: Добавлена некоторой функции оценки, дающей -1 везде, кроме +1 в некоторых небольших регионах (обратите внимание, что это может быть произвольная и не обязательно дифференцируемая скалярная функция). Стрелки теперь имеют цветовую кодировку, потому что из-за умножения мы собираемся усреднить все зеленые стрелки с положителной оценкой и отрицательные красные стрелки. Справа: после обновления параметров зеленые стрелки и перевернутые красные стрелки подталкивают нас влево и вниз. Образцы из этого распределения теперь будут иметь более высокую ожидаемую оценку, по желанию.
Я надеюсь, что связь с RL ясна. Наша политика дает нам примеры действий, и некоторые из них работают лучше, чем другие (судя по функции целесообразности). Способ изменить параметры политики состоит в том, надо выполнить прогон, взять градиент выбранных действий, умножить его на оценку и добавить все, что мы и сделали выше. Для более тщательного вывода я рекомендую лекцию
Джона Шульмана.
Обучение. Хорошо, мы разработались в принципах градиентов функции политики. Я реализовал весь подход в
130-строчном скрипте Python, который использует ATARI 2600 Pong от
OpenAI Gym. Я обучил двухслойную нейросеть с 200 нейронами скрытого слоя, используя алгоритм RMSProp для серий из 10 эпизодов (каждый эпизод по правилам состоит из нескольких розыгрышей мяча и эпизод продолжается до счета 21). Я не слишком настраивал гиперпараметры и проводил эксперимент на своем медленном Macbook, но после трехдневной тренировки я получил политику, которая играет чуть лучше, чем у встроенного игрока. Общее количество эпизодов составило приблизительно 8 000, поэтому алгоритм сыграл примерно 200 000 игр в понг, что довольно много, и произвел в общей сложности ~ 800 обновлений весов. Если бы я тренировался на GPU с ConvNets, то в течение нескольких дней, смог бы добиться больших результатов, а если оптимизировал бы гиперпараметры, то можно было бы побеждать всегда. Тем не менее, я не тратил слишком много времени на вычисления или настройку, поэтому вместо этого мы получили Pong AI, который иллюстрирует основные идеи и работает достаточно хорошо:
 Видео по ссылке. Обучающийся агент играет против алгоритмического агента
Выученные веса.
Видео по ссылке. Обучающийся агент играет против алгоритмического агента
Выученные веса. Мы также можем взглянуть на полученные веса нейросети. Благодаря предварительной обработке каждый из наших входов представляет собой разностное изображение 80x80 (текущий кадр минус предыдущий кадр). Каждый нейрон из слоя W1 соединен со скрытым слоем W2, состоящим из 200 нейронов. Количество связей равно 80*80*200. Попробуем проанализировать эти связи. Будем перебирать все нейроны слоя W2 и визуализировать, какие веса к нему ведут. Из весов, которые ведут к одному нейрону W2 от нейронов W1 сделаем картинки 80x80. Ниже представлены 40 таких картинок W2 (всего их 200). Белые пиксели — это положительные веса, а черные — отрицательные. Обратите внимание, что несколько нейронов W2 настроились на летящего мяча, закодированные пунктирными линиями. В игре мяч может находиться только в одном месте, поэтому эти нейроны являются многоцелевыми и будут «стрелять», если мяч окажется где-то внутри этих линий. Чередование черного и белого интересно, потому что, когда шар движется вдоль трассы, активность нейрона будет колебаться как синусоида. И из-за ReLU он будет «стрелять» только в отдельные позиции. На изображениях наблюдается много шума, который, был бы меньше, если бы я использовал регуляризацию L2.
 Чего не происходит.
Чего не происходит. Итак, мы научились играть в понг по картинкам используя градиент функции политики, и это работает довольно хорошо. Этот подход представляет собой причудливую форму «предположить и проверить», где «предположение» относится к прогонке нашей политики на нескольких эпизодах игры, а «проверка» приводит к поощрению действий, которые приводят к хорошим результатам. В целом это представляет собой современный уровень того, как мы в настоящее время подходим к проблемам обучения с подкреплением. Если вы поняли алгоритм интуитивно и знаете, как он работает, вы должны быть по крайней мере немного разочарованы. В частности, когда это не работает?
Сравните это с тем, как человек может научиться играть в понг. Вы сами показываете им игру и говорите что-то вроде: «Вы управляете ракеткой, и вы можете перемещать его вверх и вниз, и ваша задача – отбросить мяч мимо другого игрока, контролируемого встроенной программой», и вы готовы к работе. Обратите внимание на некоторые различия:
- На практике мы сообщаем правила и задачу игрока каким-либо образом, например, устно или письменно, на русском или английском языках. Но в стандартной задаче RL у вас имеется заранее неизвестная функция вознаграждения, которую вы должны обнаружить посредством взаимодействия с окружением. Если бы человек начал играть в понг, при этом ничего не зная о вознаграждении (особенно если бы функция вознаграждения включала бы элемент случайности), то человеку было бы очень трудно узнать, что делать. Но методика с градиентом функции политики к этому безразлична. Точно так же, если бы мы случайным образом взяли кадры и переставили пиксели, то люди, скорее всего, ничего не поймут, но наше решение с градиентом функции политики даже не смогло бы различить, особенно, если сеть полносвязанная, как тут.
- Человек носит огромное количество предварительных знаний, таких как интуитивная физика (мяч подпрыгивает, он вряд ли телепортируется, он вряд ли внезапно остановится, он поддерживает постоянную скорость и т.д.), И интуитивная психология (противник «хочет» «Чтобы выиграть, скорее всего, следует, бить по мячу так-то и так-то и т. д.). Вы также сразу понимаете концепцию «управления» ракеткой и как она реагирует на команды клавиш ВВЕРХ / ВНИЗ. Напротив, наши алгоритмы начинаются с нуля, что одновременно впечатляет (потому что он работает) и удручает (потому что у нас нет конкретных идей, как этого не делать).
- Градиенты функции политики — это грубое решение (brute force), в котором правильные действия в конечном итоге обнаруживаются и внедряются в политику, даже если они интуитивно непонятны для человека. Люди же строят богатую абстрактную модель и планируют и предугадывают действия исходя из модели. Увидя и проанализоровав понг мы можем рассуждать, что противник довольно медленный, поэтому хорошей тактикой может быть заброс мяча с высокой вертикальной скоростью, чтобы он не успел его поймать. Мы также чувствуем, что со временем мы «внедряем» хорошие решения в то, что больше похоже на политику реактивной мышечной памяти. Вы часто чувствуете, что вначале много думаете, но в конечном итоге задание становится автоматическим и безсознательным.
- С нашей абстрактной моделью игры люди могут предугадать, что может дать вознаграждение, даже не делая практических телодвижений. Эволюция научила человека тому, что ему нет уже необходимости несколько сотен раз врезаться в стену своей машиной, прежде он постепенно начнет объезжать препятствие. Он может в уме предугадать последствия того или иного действия заранее.
 Слева: Месть Монтесумы: сложная игра для наших алгоритмов RL. Игрок должен спрыгнуть, взобраться наверх, достать ключ и открыть дверь. Человек понимает, что приобретение ключа полезно. Компьютер отбирает миллиарды случайных движений, и 99% времени падает и разбивается или его убивает монстр. Другими словами, трудно «столкнуться» с положительной ситуацией. Справа: еще одна сложная игра под названием «Обморожение», в которой человек понимает, что что-то движется, что-то хорошо трогать, что-то плохо трогать, и цель состоит в том, чтобы строить иглу по кирпичику. Хороший анализ этой игры и обсуждение различий между человеческим и компьютерным подходом можно найти в статье «Создание машин, которые учатся и думают как люди».
Слева: Месть Монтесумы: сложная игра для наших алгоритмов RL. Игрок должен спрыгнуть, взобраться наверх, достать ключ и открыть дверь. Человек понимает, что приобретение ключа полезно. Компьютер отбирает миллиарды случайных движений, и 99% времени падает и разбивается или его убивает монстр. Другими словами, трудно «столкнуться» с положительной ситуацией. Справа: еще одна сложная игра под названием «Обморожение», в которой человек понимает, что что-то движется, что-то хорошо трогать, что-то плохо трогать, и цель состоит в том, чтобы строить иглу по кирпичику. Хороший анализ этой игры и обсуждение различий между человеческим и компьютерным подходом можно найти в статье «Создание машин, которые учатся и думают как люди».
Я также хотел бы подчеркнуть тот факт, что, наоборот, во многих играх градиенты политики довольно легко победили бы человека. В частности, это касается игр с частыми вознагражденими, которые требуют точной и быстрой реакции и без долгосрочного планирования. Краткосрочные корреляции между вознаграждениями и действиями могут быть легко «замечены» подходом с PG. Вы можете видеть подобное в нашем агенте Понг. Он разрабатывает стратегию, когда он просто ждет мяч, а затем быстро движется, чтобы поймать его только на самом краю, из-за чего мяч отскакивает с высокой вертикальной скоростью. Агент набирает несколько выигрышей подряд, повторяя эту незамысловатую стратегию. Есть много игр (Pinball, Breakout), в которых Deep Q-Learning уделывает и втаптывает человека в грязь своими простыми и точными действиями.
Как только вы поймете «хитрость», с помощью которой работают эти алгоритмы, вы сможете понять их сильные и слабые стороны. В частности, эти алгоритмы далеко отстают от людей в построении абстрактных представлений об играх, которые люди могут использовать для быстрого обучения. Однажды компьютер посмотрит на массив пикселей и заметит ключ, дверь и подумает про себя, что, вероятно, было бы неплохо взять ключ и добраться до двери. На данный момент нет ничего близкого к этому, и попытка попасть туда является активной областью исследований.
Недифференцируемые вычисления в нейронных сетях.Я хотел бы упомянуть еще одно интересное применение градиентов политики, не связанных с играми: оно позволяет нам проектировать и обучать нейронные сети с помощью компонентов, которые выполняют (или взаимодействуют) с недифференцируемыми вычислениями. Эта идея была впервые представлена в
Williams 1992 г. и недавно была популяризирована в
Рекуррентных моделях визуального внимания под названием «пристальное внимание» в контексте модели, которая обрабатывает изображение с последовательностью узких центрированных (foveal) взглядов низкого разрешения, подобно тому, как наш глаз осматривает предметы с помощью бегающего центрального зрения. На каждой итерации RNN получит небольшой фрагмент изображения и выберет местоположение, которое нужно посмотреть дальше. Например, RNN может посмотреть на положение (5,30), получить небольшой фрагмент изображения, затем принет решение посмотреть (24, 50) и т. д. Существует участок нейросети, который выбирает, где искать дальше, а затем осматривает его. К сожалению, эта операция недифференцируема, потому что, мы не знаем, что произошло бы, если бы мы взяли образец в другом месте. В более общем случае рассмотрим нейронную сеть, имеющую несколько входов и выходов:

Обратите внимание, что большинство синих стрелок дифференцируемы как обычно, но некоторые преобразования представления могут также включать недифференцируемую операцию выборки, которые выделены красным цветом. Мы можем просто пройти через синие стрелки в обратном направлении, но красная стрелка представляет собой зависимость, через которую мы не можем выполнить обратное распространение backprop.
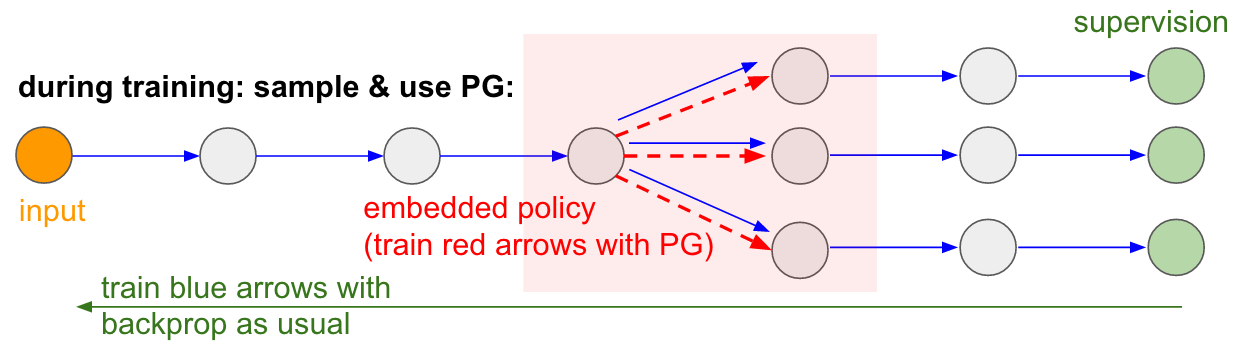
Политика градиентов на помощь! Давайте подумаем о той части сети, которая выполняет выборку, что она может быть представлена как функция стохастической политики, встроенную в большую нейросеть. Поэтому во время обучения мы произведем несколько примеров(обозначенных ветвями ниже), а затем мы будем поощрять выборки, которые в конечном итоге привели к хорошим результатам (в данном случае, например, измеренным по потерям в конце). Другими словами, мы будем обучать параметры, включенные в синие стрелки, с помощью backprop, как обычно, но параметры, включенные в красную стрелку, теперь будут обновляться независимо от обратного прохода с использованием градиентов политики, поощряя выборки, которые привели к низким потерям. Эта идея была также недавно хорошо оформлена в
оценке градиентов с использованием стохастических графов вычислений.
Тренируемый ввод/вывод в оперативную память. Вы также найдете эту идею во многих других статьях. Например, у
Neural Turing Machine есть лента памяти, с которой они читают и пишут. Чтобы выполнить операцию записи, нужно выполнить что-то вроде m [i] = x, где i и x предсказываются нейросетью RNN. Однако нет никакого сигнала, сообщающего нам, что случилось бы с функцией потерь, если бы мы записали в другое место j! = I. Поэтому NTM может выполнять «мягкие» операции чтения и записи. Он предсказывает функцию распределения внимания a, а затем выполняет for all i: m[i] = a[i]*x. Это теперь дифференцируемо, но мы должны заплатить высокую вычислительную цену, перебирая все ячейки.
Однако мы можем использовать градиенты политик, чтобы теоретически обойти эту проблему, как это сделано в
RL-NTM. Мы по-прежнему прогнозируем распределение внимания a, но вместо полного перебора мы случайно выбираем места для записи: i = sample(a); m[i] = x. Во время обучения мы могли бы делать это для небольшого набора i и, в конце концов нашли бы набор, который работал бы лучше других. Большим вычислительным преимуществом является то, что во время тестирования можно читать/писать из одной ячейки. Однако, как указано в документе, эту стратегию очень трудно заставить работать, потому что нужно перебрать много вариантов и практически случайно выйти на рабочие алгоритмы. В настоящее время исследователи согласны с тем, что PG хорошо работает только в тех случаях, когда существует несколько дискретных вариантов, когда не надо прочесывать огромные пространства поиска.
Однако с помощью градиентов политики и в тех случаях, когда доступно большое количество данных и вычислительным мощностей, мы в принципе можем мечтать о многом. Например, мы можем проектировать нейронные сети, которые учатся взаимодействовать с большими недифференцируемыми объектами, такими как Latex компиляторы. Например, чтобы char-rnn генерировал бы готовый код Latex, или систему SLAM, или решатели LQR, или что-то еще. Или, например, суперинтеллект может захотеть научиться взаимодействовать с Интернетом по TCP/IP (который, тоже не дифференцируем) для доступа к информации, необходимой для захвата мира. Это отличный пример.
Выводы
Мы увидели, что градиенты политики являются мощным общим алгоритмом, и в качестве примера мы обучили агента ATARI Pong из необработанных пикселей с нуля в
130 строках Python. В целом, тот же алгоритм можно использовать для обучения агентов для произвольных игр и, надеюсь, когда-нибудь сможем использовать для решения задач управления в реальном мире. В заключение я хотел добавить еще несколько замечаний:
О развитии AI. Мы увидели, что алгоритм работает посредством поиска методом «грубой силы», при котором вы сначала случайно колеблетесь и должны случайно натолкнуться на полезные ситуации хотя бы один раз, а в идеале часто и многократно, прежде чем функция политики изменит свои параметры. Мы также увидели, что человек подходит к этим решению этих задач совершенно по-другому, что напоминает быстрое построение абстрактной модели. Поскольку эти абстрактные модели очень сложно (если не невозможно) явно представить, это также является причиной того, что в последнее время так много интереса к генеративным моделям и программной индукции.
Об использовании в робототехнике. Алгоритм не применяется там, где трудно получить огромное количество исследований. Например, можно иметь одного (или нескольких) роботов, взаимодействующих с миром в режиме реального времени. Этого недостаточно для наивного применения алгоритма. Одним из направлений работы, предназначенным для смягчения этой проблемы, являются
детерминированные градиенты политики. Вместо того, делать реальные попытки, этот подход получает информацию о градиенте из второй нейросети (называемой критиком), который моделирует функцию оценки. Этот подход в принципе может быть эффективным с высокоразмерными действиями, где случайные выборки обеспечивают плохое покрытие. Другой связанный с этим подход заключается в расширении масштабов робототехники, что мы начинаем видеть на
ферме роботов-манипуляторов Google или, возможно, даже на модели
Tesla S+ с автопилотом.
Существует также направление работы, которое пытается сделать процесс поиска менее безнадежным, добавив дополнительный контроль. Например, во многих практических случаях можно получить начальное направление развития непосредственно от человека. Например,
AlphaGo сначала использует обучение с учителем, чтобы всего лишь предугадывать действия человека (например
удаленное управление роботами,
ученичество,
оптимизация траектории,
полный поиск политики). А получающаяся в результате политика позже настраивается с помощью PG для достижения реальной цели – для победы в игре.
В некоторых случаях может быть меньше предустановок (например, для
удаленного управления роботами), и существуют методы для использования этих данных
предварительной стажировки. Наконец, если люди не предоставляют конкретные данные или установки, они также могут в некоторых случаях получены путем расчета с использованием довольно дорогих методов оптимизации, например, путем
оптимизации траектории в известной динамической модели (такой как F = ma в физическом симуляторе) или в случаях, когда создается приблизительная локальная модель (как видно в очень многообещающей структуре управляемого поиска политики).
Об использовании PG на практике. Я хотел бы еще поговорить о RNN. Я думаю, что могло сложиться впечатление, что RNN являются магическими и автоматически решают задачи, связанные произвольными последовательностями. Правда в том, что заставить работать эти модели может быть совсем непросто. Требуется осторожность и опыт, а так же знать, когда более простые методы могут помочь вам на 90%. То же самое касается градиентов политики. Они не работают автоматически просто так: вам нужно иметь много примеров, они могут тренироваться вечно, их трудно отлаживать, когда они не работают. Всегда нужно пробовать стрелять из маленького пистолетика, прежде чем дотянуться до Базуки. Например, в случае обучения с подкреплением всегда следует проверять в первую очередь
метод кросс-энтропии (CEM), простой стохастический подход «предположи и проверь», вдохновленный эволюцией. И если вы настаиваете на том, чтобы опробовать градиенты политики для вашей задачи, убедитесь, что вы знаете опеределенные трюки. Сначала начните с простого и используйте вариант PG под названием
TRPO, который почти всегда работает лучше и последовательнее,
чем классически PG. Основная идея состоит в том, чтобы избежать обновления параметров, которые слишком сильно изменяют вашу политику, что обусловлено использованием расстояния Ку́льбака-Ле́йблера между старой и новой политикой.
На этом все! Надеюсь, я дал вам представление о том, где мы находимся с Reinforcement Learning, каковы проблемы, и если вы хотите помочь в продвижении RL, я приглашаю вас сделать это в нашем
OpenAI Gym :) До следующих встреч!
Andrej Karpathy,
исследователь, разработчик, директор подразделения ИИ и автопилота Тесла
Доп информация:
Курс о Deep Learning на пальцах 2018
https://habr.com/ru/post/414165/
Открытый курс «Deep Learning на пальцах» 2019
https://habr.com/ru/company/ods/blog/438940/
Физический Факультет НГУ
http://www.phys.nsu.ru/ 











