http://habrahabr.ru/post/242221/

Когда-то давно я решил «потрогать» Fortran. Единственную задачу которую я придумал — генерация фракталов (заодно и OpenMP в Fortran'е можно было бы попробовать). В процессе написания я часто сталкивался с проблемами, решение которых приходилось додумывать самому (например в интернете не так много примеров использования чисел двойной точности или бинарной записи в файл). Но рано или поздно все проблемы решились, и я хочу написать этот текст, который возможно кому-нибудь поможет.

Писать я буду на диалекте Fortran 90, но с GNU расширениями (те же числа двойной точности).

Немного теории о фракталах

Фрактал (fractus – дробленый, сломанный, разбитый) — в узком смысле, сложная геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком.

Существует большая группа фракталов — алгебраические фракталы. Это название вытекает из принципа построения таких фракталов. Для их построения используют рекурсивные функции. Например алгебраическими фракталами являются: Множество Жюлиа, Множество Мандельброта, Бассейн(фрактал) Ньютона.

Построение алгебраических фракталов

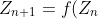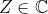
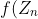Один из методов построения представляет собой итерационный расчет , где , а некая функция. Расчет данной функции продолжается до выполнения определенного условия. Когда это условие выполнится на экран выводится точка.

Поведение функции для разных точек комплексной плоскости может иметь разное поведение:

• Стремится к бесконечности
• Стремится к 0
• Принимает несколько фиксированных значений и не выходит за их пределы
• Хаотичное поведение. Отсутствие каких либо тенденций

Один из простейших (как для понимания, так и для реализации) алгоритмов построения алгебраических фракталов известен как «escape time algorithm». Если кратко, то производится итеративный расчет числа для каждой точки комплексной плоскости.

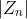
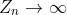
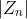
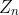
Было доказано, что если окажется больше bailout, то последовательность . Сравнение с bailout позволяет находить точки лежащие вне множества. Для точек, лежащих вне множества, последовательность не будет иметь тенденции к бесконечности, поэтому никогда не достигнет bailout.

Я рассмотрю два простых фрактала – Множество Жюлиа и Множество Мандельброта. Расчитываются они по одной и той-же функции, а отличаются лишь константой, где у Жюлиа это постоянная константа, а у Мандельброба константа зависит от точки комплексной плоскости.

Построение Множества Жюлиа

Начало и конец программы простой и тривиальный:

program frac
end

Дальше нам нужно ввести несколько констант:

	INTEGER, PARAMETER :: iterations = 2048 !Количество итераций. Чем больше, тем глубже будет идти просчет

	REAL(8), PARAMETER :: mag_ratio = 1.0_8 !Приближение

	REAL(8), PARAMETER :: x0 = 0.0_8 !Смещение комплексной плоскости
	REAL(8), PARAMETER :: y0 = 0.0_8 !

	INTEGER, PARAMETER :: resox = 1024 !Разрешение получившегося изображения
	INTEGER, PARAMETER :: resoy = resox

	REAL(8), PARAMETER :: xshift = (-1.5_8 / mag_ratio) + x0 !Смещение центра комплексной оси в
	REAL(8), PARAMETER :: yshift = (-1.5_8 / mag_ratio) + y0 !центр изображения

	REAL(8), PARAMETER :: CXmin = -1.5_8 / mag_ratio !Следующие константы растягивают
	REAL(8), PARAMETER :: CXmax = 1.5_8 / mag_ratio  !комплексную плоскость до размеров resox x resoy
	REAL(8), PARAMETER :: CXshag = (DABS(CXmin) + DABS(CXmax)) / resox !Связываем значение одного пикселя и точки на комплексной плоскости
	REAL(8), PARAMETER :: CYmin = -1.5_8 / mag_ratio
	REAL(8), PARAMETER :: CYmax = 1.5_8 / mag_ratio
	REAL(8), PARAMETER :: CYshag = (DABS(CYmin) + DABS(CYmax)) / resoy

	COMPLEX(8), PARAMETER :: c = DCMPLX(0.285_8, 0.01_8) !Наша основная константа

И вот тут нужно кое-что объяснить. REAL и COMPLEX это число с плавающей точкой одинарной точности и комплексное число, состоящее из двух REAL. REAL(8) это число двойной точности, а COMPLEX(8), соотвественно, комплексное число, состоящее из двух REAL(8). Так-же к стандартным функциям добавляется литера D (как в случае с ABS), что указывает на использование чисел двойной точности.

Дальше нам нужно ввести несколько переменных:

	CHARACTER, DIMENSION(:), ALLOCATABLE :: matrix !Массив точек

	COMPLEX(8) :: z
	INTEGER :: x, y, iter
	REAL(8) :: iter2 !Понадобится нам для сглаживания

	ALLOCATE(matrix(resox * resoy * 3))

Использование ALLOCATABLE обязательно! Т.к. в ином случае:

	CHARACTER, DIMENSION(0:resox * resoy * 3) :: matrix !Массив точек

Память у нас выделится на стеке, а это не приемлемо при использовании в нескольких потоках. Поэтому мы выделяем память на куче.

Так-же я не использую двумерные массивы, т.к. при выделении на куче массив будет занимать больше места, да и записать его в файл будет сложнее.

Дальше нам нужно указать количество потоков, порождаемых OpenMP:

	call omp_set_num_threads(16)

А тут начинаются непосредственно вычисления. В Fortran'е директивы для OpenMP указываются через коментарии (в C/C++ для это есть специльный макрос #pragma).

	!$OMP PARALLEL DO PRIVATE(iter, iter2, z)
	do x = 0, resox-1
		do y = 0, resoy-1
			iter = 0 !Обнуляем количество итераций
			z = DCMPLX(x * CXshag + xshift, y * CYshag + yshift) !Задаем Z начальное значение
			do while ((iter .le. iterations) .and. (CDABS(z) .le. 4.0_8)) !Обычно за bailout берут 2, но я взял 4, т.к. результат лучше сглаживается
				z = z**2 + c
				iter = iter + 1
			end do

			iter2 = REAL(iter) - DLOG(DLOG(CDABS(z))) / DLOG(2.0_8) !Формула для сглаживания iter-ln(log2(|Z|))
			matrix((x + y * resox) * 3 + 0) = CHAR(NINT(DMOD(iter2 * 7.0_8, 256.0_8))) !Один из способов расскрашивания
			matrix((x + y * resox) * 3 + 1) = CHAR(NINT(DMOD(iter2 * 14.0_8, 256.0_8)))
			matrix((x + y * resox) * 3 + 2) = CHAR(NINT(DMOD(iter2 * 2.0_8, 256.0_8)))
		end do
	end do
	!$OMP END PARALLEL DO

Самая трудоемкая часть закончена. Дальше нам остается вывести информацию в удобном для восприятия виде — изображение. Я буду использовать формат PNM, т.к. это самый простой формат изображений.

PNM состоит из нескольких секций:

P6
#Комментарий
1024 1024
255

Первая строчка это указание формата записи информации о пикселях:

• P1/P4 — черно-белое изображение
• P2/P5 — серое изображение
• P3/P6 — цветное изображение

Первая P это вариант, где цвет пикселя записывается ASCII символом, а вторая P дает возможность записывать цвет пикселя в бинарном виде (что значительно экономит место на диске).

Следующей строкой идет комментарий, дальше разрешение изображения и количество цветов на пиксель. После количества цветов идет непосредственно информация о пикселях.

Начинаем записывать изображение в файл:

	open(unit=8, file = trim("test.pnm"))
	write(8, '(a)') "P6" !(a) это текстовая строка
	write(8, '(a)') ""
	write(8, '(I0, a, I0)') resox, ' ', resoy
	write(8, '(I0)') 255
	write(8, *) matrix
	close(8)

	DEALLOCATE(matrix)

DEALLOCATE мы выполняем для приличия, ибо при выходе из программы, ОС все равно вернет занятую память системе.

Для сборки программы можно использовать компилятор от GNU — gfortran:

gfortran -std=gnu frac.f90 -o frac.run -fopenmp

Должно получится следующее изображение:

Как сгенерировать Множество Мандельброта

Это сделать несложно, достаточно заменить c и изменить несколько констант. В данном случаем убираем константу c и добавляем переменную c:

	COMPLEX(8) :: z, c

			z = DCMPLX(x * CXshag + xshift, y * CYshag + yshift) !Задаем Z начальное значение
			c = z

А так-же меняем старые константы:

	INTEGER, PARAMETER :: MAIN_RES = 1024
	INTEGER, PARAMETER :: resox = (MAIN_RES / 3) * 3
	INTEGER, PARAMETER :: resoy = (resox * 2) / 3

	REAL(8), PARAMETER :: xshift = (-2.0_8 / mag_ratio) + x0
	REAL(8), PARAMETER :: yshift = (-1.0_8 / mag_ratio) + y0

	REAL(8), PARAMETER :: CXmin = -2.0_8 / mag_ratio
	REAL(8), PARAMETER :: CXmax = 1.0_8 / mag_ratio
	REAL(8), PARAMETER :: CXshag = (DABS(CXmin) + DABS(CXmax)) / resox
	REAL(8), PARAMETER :: CYmin = -1.0_8 / mag_ratio
	REAL(8), PARAMETER :: CYmax = 1.0_8 / mag_ratio
	REAL(8), PARAMETER :: CYshag = (DABS(CYmin) + DABS(CYmax)) / resoy

Должно получится следующее изображение:

Используемая литература

en.wikipedia.org/wiki/Fractal
en.wikipedia.org/wiki/Julia_set
en.wikipedia.org/wiki/Mandelbrot_set
en.wikipedia.org/wiki/OpenMP
openmp.org/wp/openmp-specifications/
gcc.gnu.org/onlinedocs/gfortran/