Всем привет! Если перед вами стоит задача проведения А/Б тестирования, то я помогу вам понять, как с помощью python сформировать однородные группы с помощью алгоритмов сходства объектов на основе косинусного и взвешенного косинусного расстояния для его проведения.

Довольно часто в аналитической работе приходится сталкиваться с необходимостью проведения А/Б (сплит) тестирования в том или ином виде. Общая идея сплит-тестирования в максимально упрощённом виде заключается в следующем: выбирается набор объектов, в идеальном случае максимально похожих друг с другом, делится на две группы, обычно равные по численности, затем одна группа (будем также называть её группой А или тестовой группой) приобретает признак, который не приобретает другая (группа Б или контрольная), и через определенное время сравниваются показатели изменения целевых метрик в обеих группах, на основании чего оценивается влияние приобретения исследуемого признака объектами.

Обычно, такие тестирования проводятся в настоящем времени: к примеру, когда компания хочет протестировать на пользователях новые обновления, она проводит А/Б-тесты. Однако и для аналитики исторических данных тоже иногда можно применить стратегию, поддающуюся описанию в парадигме сплит-тестирований: например, когда Ваша задача состоит в проверке эффективности введения того или иного новшества в процессе или продукте, а анализировать Вы можете только исторические данные. Если удастся хорошо выбрать группы А и Б, Вы сможете проследить исторические изменения в них и сделать интересующиеся Вас выводы. В данной работе мы не будем углубляться в то, как проводится анализ результатов А/Б-тестирования, нас интересует этап подготовки данных.

Для проведения качественного А/Б-тестирования нам важно подобрать объекты в тестовой и контрольной группах максимально похожими по характеристикам. В дальнейшем будем исходить из того предположения, что основной является тестовая группа, так как на практике чаще может встретиться задача, где нет свободного выбора именно тестовой группы, например, при анализе исторических данных и в других случаях, когда кандидатов в контрольную группу заведомо намного больше. Одним из самых сложных вопросов во всём процессе подготовки групп остаётся: как выделить похожие объекты (сделать выборки однородными), кроме как вручную? На помощь приходят векторные представления и статистические меры схожести векторов. Ниже рассмотрим подробнее некоторые из них и способы их применения к нашей задаче.

Косинусное расстояние между векторами признаков объектов. Математически, идея состоит вот в чём: каждый объект со своим набором признаков представляется как вектор в n-мерном признаковом пространстве, где n – количество признаков. Затем, между каждыми двумя векторами возможно посчитать косинус угла a между ними и определить косинусное расстояние между ними, как 1 – cos (a). Это можно интерпретировать как меру схожести наших объектов. Таким образом, выделив среднего клиента в тестовой группе и сравнив вектор каждого предполагаемого клиента контрольной и тестовой группы с ним, можно оставить лишь тех, у которых косинусное расстояние между ними и нашим опорным вектором среднего клиента целевой группы минимально, при этом условимся, что для наших исследований важно проследить, чтобы численность людей в итоговых группах была одинаковой. Дискуссионным вопросом здесь является выбор порога. Он уже подбирается экспериментально (косинусное расстояние может принимать значения от 0 до 2). Приведём для наглядности несколько двумерных векторов:

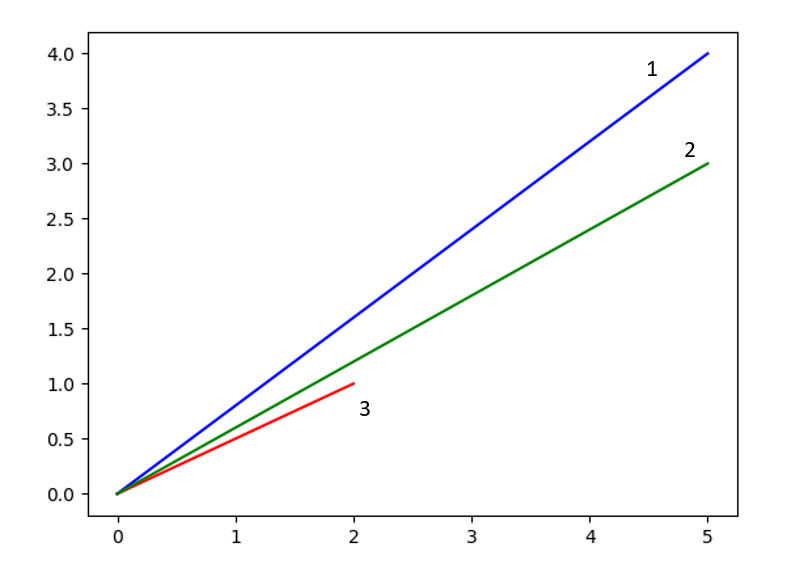
Технически алгоритм нахождения косинусного расстояния между двумя векторами реализован в библиотеке SciPy на python, мы же приведём реализацию функции, решающей непосредственно нашу задачу, то есть принимающей на вход два pandas-датасета (из одного требуется сформировать тестовую группу, из другого контрольную) и выдающей преобразованные равные по размеру датафрейма однородных по признакам объектов. В каждой строке входных таблиц должны быть записаны значения признаков (характеристик) объектов, преобразованные к числовому формату:

import pandas as pd
import numpy as np
from scipy import spatial

def form_groups_cosine(A, B, threshold=2):
    assert all(pd.api.types.is_numeric_dtype(A[col]) for col in A.columns), 'Таблицы должны содержать только числовой формат данных. Преобразуйте или избавьтесь от категориальных признаков'
    assert all(pd.api.types.is_numeric_dtype(B[col]) for col in B.columns), 'Таблицы должны содержать только числовой формат данных. Преобразуйте или избавьтесь от категориальных признаков'
    assert len(A) != 0 and len(B) != 0, 'Таблицы должны быть непусты'
	assert A.shape[1] == B.shape[1], 'Признаки у клиентов разных групп должны быть одинаковыми!'

    distances_A = []
    distances_B = []
    A_ = A.to_numpy()
    B_ = B.to_numpy()
    A_mean_vector = np.mean(A_, axis=0) 
    
    for i, object_ in enumerate(A_):
        if np.count_nonzero(object_) == 0:
            continue
        distance = spatial.distance.cosine(object_, 	 A_mean_vector)
        if distance <= threshold:
            distances_A.append([i, distance])
            
    for i, object_ in enumerate(B_):
        if np.count_nonzero(object_) == 0:
            continue
        distance = spatial.distance.cosine(object_, A_mean_vector)
        if distance <= threshold:
            distances_B.append([i, distance])
            
    distances_A.sort(key=lambda i: i[1])
    distances_B.sort(key=lambda i: i[1])

	assert distances_A != [] and distances_B != [], 'При заданном 	Вами пороге нельзя подобрать похожие векторы в данных 	датасетах'

    if len(distances_A) <= len(distances_B):
        distances_B = np.array(distances_B)[:len(distances_A)].T[0]
        distances_A = np.array(distances_A).T[0]
    else:
        distances_A = np.array(distances_A)[:len(distances_B)].T[0]
        distances_B = np.array(distances_B).T[0]
    A = A.loc[A.index.isin(distances_A)]
    B = B.loc[B.index.isin(distances_B)]
    return A, B

Но при фильтрации на основе косинусного расстояния мы сталкиваемся с проблемой: допустим, мы имеем векторы [3,3] и [1,1], они будут иметь почти нулевое косинусное расстояние между друг другом, но ведь объекты могут являться фактически очень разными, просто их признаки отличаются в пропорциональное число раз. В таком случае имеет смысл использовать взвешенное косинусное расстояние (adjusted cosine distance). Суть его в том, что, в отличие от классического косинусного расстояния, перед вычислением косинуса, из каждого признака вычитается среднее по этому признаку среди объектов данной группы или какая-то функция от среднего. Таким образом нивелируется ошибка от сонаправленности векторов сильно отличающихся друг от друга объектов. В нашем примере среднее будет равно 2 для каждого признака. После такого преобразования векторы объектов станут противоположно направлены. ([1,1] и [-1,-1]) Также приведённый выше алгоритм сходства групп на основе косинусного расстояния не учитывает возможную различную значимость признаков, ведь для конкретного исследования некоторые критерии похожести могут быть важнее других, учтём это при написании алгоритма со взвешенным косинусным расстоянием. Общий стиль программной реализации почти не отличается от фильтрации по косинусному расстоянию, разве что модифицируется метод сравнения и теперь мы добавим в параметры функции массив весов признаков, заранее аналитически определённых. Приведём реализацию фильтрации групп с помощью данного алгоритма на Python:

import pandas as pd
import numpy as np
from scipy import spatial

def form_groups_adjusted_cosine(A, B, feature_weights=None, threshold=2):
    assert all(pd.api.types.is_numeric_dtype(A[col]) for col in A.columns), 'Таблицы должны содержать только числовой формат данных. Преобразуйте или избавьтесь от категориальных признаков'
    assert all(pd.api.types.is_numeric_dtype(B[col]) for col in B.columns), 'Таблицы должны содержать только числовой формат данных. Преобразуйте или избавьтесь от категориальных признаков'
    assert len(A) != 0 and len(B) != 0, 'Таблицы должны быть непусты'
    assert A.shape[1] == B.shape[1], 'Признаки у клиентов разных групп должны быть одинаковыми!'
    if feature_weights == None:
        feature_weights = np.ones(A.shape[1])   
    else:
         assert A.shape[1] == len(feature_weights), 'Проверьте признаки в векторе весов'
    distances_A = []
    distances_B = []

    A_ = A.to_numpy()
    B_ = B.to_numpy()

    A_ = A_ * feature_weights
    B_ = B_ * feature_weights

    A_mean_vector = np.mean(A_, axis=0)
    
    for i, object_ in enumerate(A_):
        if np.count_nonzero(object_) == 0:
            continue
        distance = spatial.distance.cosine(object_ - np.mean(A_, axis=0)/2, A_mean_vector - np.mean(A_, axis=0)/2)
        if distance <= threshold:
            distances_A.append([i, distance])
            
    for i, object_ in enumerate(B_):
        if np.count_nonzero(object_) == 0:
            continue
        distance = spatial.distance.cosine(object_ - np.mean(B_, axis=0), A_mean_vector - np.mean(B_, axis=0))
        if distance <= threshold:
            distances_B.append([i, distance])
            
    distances_A.sort(key=lambda i: i[1])
    distances_B.sort(key=lambda i: i[1])
    assert distances_A != [] and distances_B != [], 'При заданном Вами пороге нельзя подобрать похожие векторы в данных датасетах'
    if len(distances_A) <= len(distances_B):
        distances_B = np.array(distances_B)[:len(distances_A)].T[0]
        distances_A = np.array(distances_A).T[0]
    else:
        distances_A = np.array(distances_A)[:len(distances_B)].T[0]
        distances_B = np.array(distances_B).T[0]
    A = A.loc[A.index.isin(distances_A)]
    B = B.loc[B.index.isin(distances_B)]
    return A, B

Таким образом, подав в функции в качестве входных данных два необязательно равных набора объектов, вектор весов признаков и, при желании, порог косинусного расстояния, мы получаем на выходе функции два равных по численности набора объектов, схожих между собой.

Приведем пример отработки данного алгоритма на тестовых синтетических данных:

Пусть нам даны два набора клиентов с признаками A, B, C, в одном 4 клиента (группа B), в другом 3 (группа А):

Подадим для примера эти наборы в функцию form_groups_adjusted_cosine() с порогом максимального косинусного расстояния, равным 1:

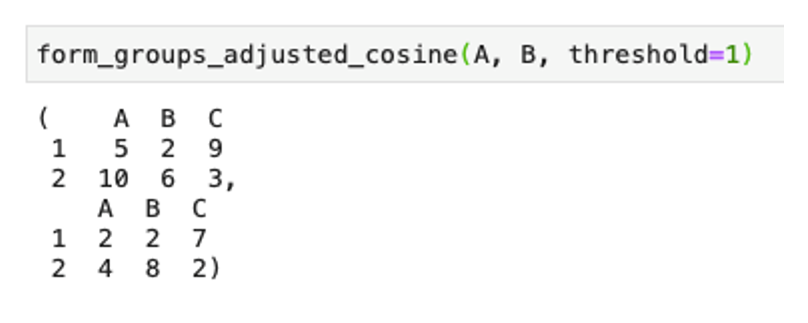
Мы получили два равных набора по два клиента. Заметим, убрались как раз выбивающиеся по значениям признаков клиенты и группы стали равны по размеру.

Мы рассмотрели основные и достаточно простые методы фильтрации объектов для формирования однородных групп для А/Б-тестирования. Приведённые в этой работе реализации могут быть полезны всем специалистам, сталкивающимся с проблемой неоднородности выборок в сплит-тестах.