Дисковое кеширование деревьев ленивых вычислений
- среда, 12 сентября 2018 г. в 00:19:30
О концепции ленивых вычислений вряд ли стоит подробно говорить. Идея пореже делать одно и то же, особенно, если оно долгое и тяжелое, стара как мир. Потому сразу к делу.
По разумению автора настоящего текста нормальный ленификатор должен:

По порядку:
Эта цепочка рассуждений привела к техническому решению, оформленному в python библиотеку evalcache (ссылки в конце статьи).
import evalcache
import hashlib
import shelve
lazy = evalcache.Lazy(cache = shelve.open(".cache"), algo = hashlib.sha256)
@lazy
def summ(a,b,c):
return a + b + c
@lazy
def sqr(a):
return a * a
a = 1
b = sqr(2)
c = lazy(3)
lazyresult = summ(a, b, c)
result = lazyresult.unlazy()
print(lazyresult) #f8a871cd8c85850f6bf2ec96b223de2d302dd7f38c749867c2851deb0b24315c
print(result) #8Как это работает?
Первое, что здесь бросается в глаза, создание декоратора lazy. Такое синтаксическое решение довольно стандартно для питоновских ленификаторов. Декоратору lazy передается объект кэша, в котором ленификатор будет хранить результаты вычислений. На тип кэша накладывается требования dict-like интерфейса. Иными словами, мы умеем кешировать во всё, что реализует тот же интерфейс, что есть у типа dict. Для демонстрации в примере выше использован словарь из библиотеки shelve.
Также декоратору передаются протокол хеширования, которые он будет использовать для построения хэшключей объектов и некоторые дополнительные опции (разрешение записи, разрешение чтения, отладочный вывод), с которыми можно ознакомиться в документации или коде.
Декоратор может быть применен как к функциям, так и к объектам других типов. В этот момент на их основе строится ленивый объект с хэшключем, расчитанным на основе репрезентации (или с помощью специально определенной для данного типа хэшфункции).
Ключевой особенностью библиотеки является то, что ленивый объект может порождать другие ленивые объекты, причем хэшключ родителя (или родителей) будет подмешан в хэш ключ потомка. Для ленивых объектов допускается использование операции взятия атрибута, использование вызовов(__call__) объектов, применение операторов.
При проходе по скрипту, на самом деле, не производится никаких вычислений. Для b не расчитывается квадрат, а для lazyresult не считается сумма аргументов. Вместо этого строится дерево операций и подсчитываются хэшключи ленивых объектов.
Реальные вычисления (если результат ранее не положен в кэш) будут выполнены только в строке: result = lazyresult.unlazy()
Если объект был вычислен ранее, он будет подгружен из файла.
Можно визуализировать дерево построения:
evalcache.print_tree(lazyresult)
...
generic:
<function summ at 0x7f1cfc0d5048>
args:
1
generic:
<function sqr at 0x7f1cf9af29d8>
args:
2
-------
3
-------Поскольку хэши объектов строятся на основе данных о порождающих эти объекты аргументах, при изменении аргумента, хэш объекта изменяется и вместе с ним каскадно изменяются хэши всей зависящей от него цепочки. Это позволяет поддерживать данные кэша в актуальном состоянии, вовремя производя обновления.
Ленивые объекты выстраиваются в дерево. Если мы производим операцию unlazy над одним из объектов, будет загружено и пересчитано ровно столько объектов, сколько необходимо для получения валидного результата. В идеале — просто загрузится необходимый объект. В этом случае алгоритм не будет подтягивать в память образующие объекты.
Выше был простой пример, который показывает синтаксис, но не демонстрирует вычислительной мощи подхода.
Вот пример чуть более приближенный к реальной жизни (используется sympy).
#!/usr/bin/python3.5
from sympy import *
import numpy as np
import math
import evalcache
lazy = evalcache.Lazy(evalcache.DirCache(".evalcache"), diag = True)
pj1, psi, y0, gamma, gr= symbols("pj1 psi y0 gamma gr")
###################### Construct sympy expression #####################
F = 2500
xright = 625
re = 625
y0 = 1650
gr = 2*math.pi / 360
#gamma = pi / 2
xj1q = xright + re * (1 - cos(psi))
yj1q = (xright + re) * tan(psi) - re * sin(psi) #+ y0
pj1 = sqrt(xj1q**2 + yj1q**2)
pj2 = pj1 + y0 * sin(psi)
zj2 = (pj2**2)/4/F
asqrt = sqrt(pj2**2 + 4*F**2)
xp2 = 2*F / asqrt
yp2 = pj2 / asqrt
xp3 = yp2
yp3 = -xp2
xmpsi = 1295
gmpsi = 106 * gr
aepsi = 600
bepsi = 125
b = 0.5*(1-cos(pi * gamma / gmpsi))
p1 = (
(gamma * xmpsi / gmpsi * xp2) * (1-b)
+ (aepsi * xp2 * sin(gamma) + bepsi * yp2 * (1-cos(gamma)))*b + pj1
)
#######################################################################
#First lazy node. Simplify is long operation.
#Sympy has very good representations for expressions
print("Expression:", repr(p1))
print()
p1 = lazy(simplify)(p1)
#########################################################################################
## Really don't need to lazify fast operations
Na = 200
angles = [t * 2 * math.pi / 360 / Na * 106 for t in range(0,Na+1)]
N = int(200)
a = (np.arange(0,N+1) - N/2) * 90/360*2*math.pi/N
#########################################################################################
@lazy
def genarray(angles, a, p1):
points = []
for i in range(0, len(angles)):
ex = p1.subs(gamma, angles[i])
func = lambdify(psi, ex, 'numpy') # returns a numpy-ready function
rads = func(a)
xs = rads*np.cos(a)
ys = rads*np.sin(a)
arr = np.column_stack((xs,ys,[i*2]*len(xs)))
points.append(arr)
return points
#Second lazy node.
arr = genarray(angles, a, p1).unlazy()
print("\nResult list:", arr.__class__, len(arr))Операции по упрощению символьных выражений крайне затратны и буквально просятся в ленификацию. Дальнейшее построение большого массива выполняется еще дольше, но благодаря ленификации, результаты будут подтягиваться из кэша. Обратите внимания, что если в верхней части скрипта, где генерируется sympy выражение, будут изменены какие-то коэффициенты, результаты будут пересчитаны, потому что хэшключ ленивого объекта изменится (спасибо крутым __repr__ операторам sympy).
Довольно часто встречается ситуация, когда исследователь проводит вычислительные эксперименты над длительное время генерируемым объектом. Он может использовать несколько скриптов для разделения генерации и использования объекта, что может порождать проблемы с несвоевременным обновлением данных. Предложенный подход может облегчить этот кейс.
evalcache — часть проекта zencad. Это маленький скриптовый кадик, вдохновленный и эксплуатирующий те же идеи, что и openscad. В отличие от mesh ориентированного openscad, в zencad, работающем на ядре opencascade используется brep представление объектов, а скрипты пишутся на языке python.
Геометрические операции зачастую выполняются долго. Недостаток скриптовых cad систем в том, что каждый раз при запуске скрипта, изделие полностью пересчитывается заново. Причем с ростом и усложнением модели, накладные расходы растут отнюдь не линейно. Это приводит к тому, что комфортно работать можно только с крайне небольшими моделями.
Задача evalcache состояла в том, чтобы сгладить эту проблему. В zencad все операции объявлены как ленивые.
Примеры:
#!/usr/bin/python3
#coding: utf-8
from zencad import *
xgate = 14.65
ygate = 11.6
zgate = 11
t = (xgate - 11.7) / 2
ear_r = 8.6/2
ear_w = 7.8 - ear_r
ear_z = 3
hx_h = 2.0
bx = xgate + ear_w
by = 2
bz = ear_z+1
gate = (
box(xgate, ygate, t).up(zgate - t) +
box(t, ygate, zgate) +
box(t, ygate, zgate).right(xgate - t)
)
gate = gate.fillet(1, [5, 23,29, 76])
gate = gate.left(xgate/2)
ear = (box(ear_w, ear_r * 2, ear_z) + cylinder(r = ear_r, h = ear_z).forw(ear_r).right(ear_w)).right(xgate/2 - t)
hx = linear_extrude( ngon(r = 2.5, n = 6).rotateZ(deg(90)).forw(ear_r), hx_h ).up(ear_z - hx_h).right(xgate/2 -t + ear_w)
m = (
gate
+ ear
+ ear.mirrorYZ()
- hx
- hx.mirrorYZ()
- box(xgate-2*t, ygate, zgate, center = True).forw(ygate/2)
- box(bx, by, bz, center = True).forw(ear_r).up(bz/2)
- cylinder(r = 2/2, h = 100, center = True).right(xgate/2-t+ear_w).forw(ear_r)
- cylinder(r = 2/2, h = 100, center = True).left(xgate/2-t+ear_w).forw(ear_r)
)
display(m)
show()Этот скрипт генерирует следующую модель:
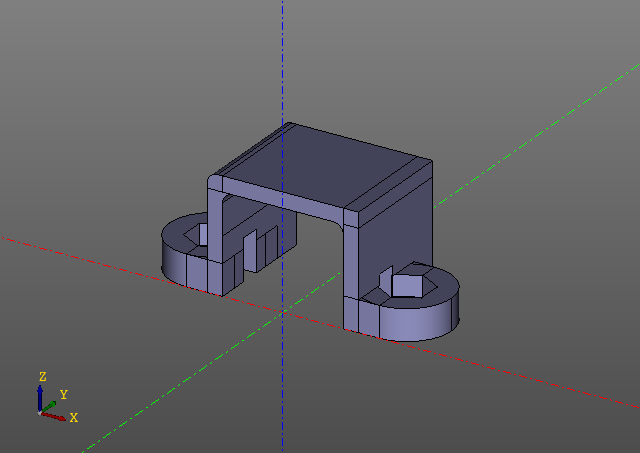
Обратите внимание, что ни одного вызова evalcache в скрипте нет. Фокус в том, что ленификация заложена в саму библиотеку zencad и снаружи ее на первый взгляд даже и не видно, хотя вся работа здесь — работа с ленивыми объектами, а непосредственное вычисление производится только в функции 'display'. Разумеется, если какой-то параметр модели будет изменен, модель будет пересчитана с того места, где изменился первый хэшключ.
Вот еще один пример. В этот раз ограничимся картинками:
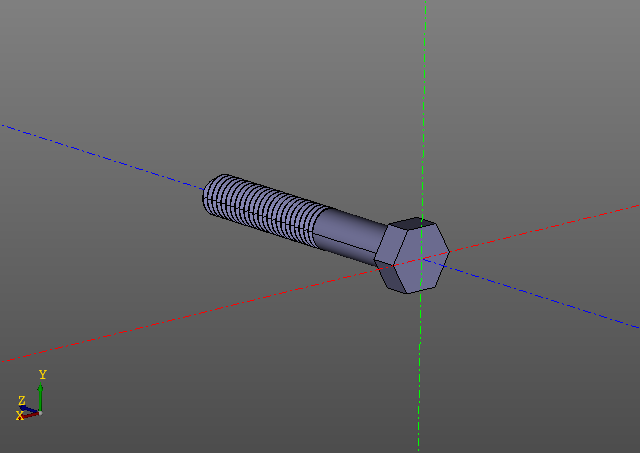
Вычисление резьбовой поверхности задача не из легких. На моем компьютере такой болт строится порядка десяти секунд… Редактировать модель с резьбами горазда приятнее, используя кеширование.
А теперь это чудо:

Пересечение резьбовых поверхностей — сложная расчетная задача. Практической ценности, впрочем никакой, кроме проверки математики. Вычисление занимает полторы минуты. Достойная цель для ленификации.
Кэш может отрабатывать не так, как задумано.
Ошибки кэша можно разделить на ложноположительные и ложноотрицательные.
Ложноотрицательные ошибки — это ситуации, когда результат вычисления в кэше есть, но система его не нашла.
Это бывает в случае, если алгоритм построения хэшключа, которым пользуется evalcache по какой-то причине выдал отличающийся ключ на повторное вычисление. Если для объекта кэшируемого типа не переопределена хэшфункция, evalcache использует __repr__ объекта для построения ключа.
Ошибка случается, например, если ленифицируемый класс не переопределяет стандартный object.__repr__, который изменяется от запуска к запуску. Или, если переопределенный __repr__, как-то зависит от незначимых для вычисления изменяющихся данных (вроде адреса объекта или временной метки).
Плохо:
class A:
def __init__(self):
self.i = 3
A_lazy = lazy(A)
A_lazy().unlazy() #Этот объект никогда не будет подгружаться из кэша из-за плохого __repr__.Хорошо:
class A:
def __init__(self):
self.i = 3
def __repr__(self):
return "A({})".format(self.i)
A_lazy = lazy(A)
A_lazy().unlazy() #Этот объект будет подгружаться из кэша.Ложноотрицательные ошибки приводят к тому, что ленификация не работает. Объект будет пересчитываться при каждом новом выполнении скрипта.
Это более мерзкий тип ошибки, так как приводит к ошибкам в конечном объекте вычисления:
Может случаться по двум причинам.
class A:
def __init__(self):
self.i = 3
def __repr__(self):
return "({})".format(self.i)
class B:
def __init__(self):
self.i = 3
def __repr__(self):
return "({})".format(self.i)
A_lazy = lazy(A)
B_lazy = lazy(B)
a = A_lazy().unlazy()
b = B_lazy().unlazy() #Ошибка. Вместо генерации объекта класса B, мы получим только что сохраненный объект класса A. Обе проблемы связаны с несовместимым __repr__ объекта. Если по какой-то причине переписать типу объекта __repr__ метод нельзя, библиотека позволяет задать для пользовательского типа специальную хэшфункцию.
Есть много библиотек ленификации, которые в основном считают достаточным выполнение вычисления не более одного раза за вызов скрипта.
Есть много библиотек дискового кэширования, которые по вашей просьбе сохранят для вас объект с необходимым ключом.
Но библиотек, которые позволяли бы кэшировать результаты по дереву исполнения, я все же не нашел. Если они есть, пожалуйста, отсемафорьте.
Ссылки: