http://habrahabr.ru/post/229959/
 Данный пост является продолжением моей статьи [1] на Хабрахабре об аттракторе Лоренца. Здесь рассмотрим метод построения приближенных решений соответствующей системы, уделив внимание программной реализации.
Данный пост является продолжением моей статьи [1] на Хабрахабре об аттракторе Лоренца. Здесь рассмотрим метод построения приближенных решений соответствующей системы, уделив внимание программной реализации.
Динамической системой Лоренца является автономная система обыкновенных дифференциальных уравнений третьего порядка

где

,
r и
b являются положительными числами. Для исследования поведения решений системы обычно берут классические значения параметров системы, т.е.

Как было отмечено в статье [1], в этом случае в системе (1) имеет место неустойчивость ее решений на аттракторе. По сути, это делает некорректным применение классических численных методов на больших отрезках времени (а на таких отрезках и строятся притягивающие множества динамических систем). Одним из вариантов преодоления этой проблемы является переход к высокоточным вычислениям, но такой подход ставит исследователя в жесткие рамки: во-первых, малая степень свободы для уменьшения ошибки (изменение величины шага

интегрирования и точности представления вещественного числа для управления вычислительным процессом), во-вторых, большой объем вычислений при очень малых

.
Другим вариантом решения данной проблемы может быть применение метода степенных рядов. В работе [2] описана модификация этого метода для динамических систем вида (1), позволяющая достаточно быстро определять коэффициенты разложений

как

где коэффициенты

,

и

определяются начальными условиями; также получена длина (шаг)

отрезка сходимости рядов (2):

если

, то

, иначе

,

— любое положительное число.
Заметим, что приведенная в статье [2] схема получения длины отрезка сходимости степенных рядов может по аналогии перенесена на другие динамические системы третьего порядка с нелинейностями вида (1) (например, система, описывающая поведение саморазвивающейся рыночной экономики [3, с. 261]).
Несмотря на то, что все траектории системы (1) ограничены и ее правая часть всюду аналитична, первоначальный вычислительный эксперимент показал, что радиус сходимости рядов (2) ограничен и зависит от выбора начальных условий. Поэтому описанным способом мы можем получить только часть траектории. Процедура построения дуги траектории на любом отрезке времени заключается в сшивке частей траектории, составляющих искомое решение, на которых сходятся ряды (2). Ошибкой интегрирования, накапливаемой при переходе от дуги к дуге траектории из-за погрешности нахождения текущего приближенного решения, можно управлять за счет варьирования точности разложения в степенной ряд. Использование при этом высокоточных вычислений позволяет продолжить решения на очень большие промежутки времени, поскольку точность разложения в ряд невозможно сделать сколь угодно малой из-за ограничения на машинный эпсилон.
По формулам (3) вычисляем

,

и

до такого значения
i, при котором имеет место оценка для заданной точности
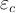
вычислений

Понятно, что значительного накопления ошибки интегрирования на длинных временных отрезках нам и здесь не избежать, поэтому будем реализовывать высокоточные вычисления с плавающей точкой на базе библиотеки
GNU MPFR Library, а точнее, C++-интерфейс библиотеки MPFR для работы с вещественными числами произвольной точности —
MPFR C++. Она удобна тем, что в ней имеется класс mpreal с перегруженными арифметическими операциями и дружественными математическими функциями. Для установки библиотеки в Ubuntu Linux выполним
sudo apt-get install libmpfrc++-dev
Кроме пакета libmpfr-dev менеджеров пакетов потянет еще и libgmp-dev. Это devel-пакет библиотеки
GNU Multiple Precision Arithmetic Library или GMP (MPFR является ее расширением).
Рассмотрим пример кода на C++ вычисления значений фазовых координат в конечный момент времени, а также проверки найденных значений.
#include <iostream>
#include <vector>
using namespace std;
#include <mpreal.h>
using namespace mpfr;
// Точность по степенному ряду
#define eps_c "1e-50"
// Параметры системы уравнений Лоренца
#define sigma 10
#define r 28
#define b 8/(mpreal)3
// Количество бит под мантиссу вещественного числа
#define prec 180
// Как считать шаг: 1 - по оценке отрезка сходимости, 0 - заданная величина
#define FL_CALC 1
// Фиксированный шаг по времени
#define step_t "0.02"
// Функция возвращает длину отрезка сходимости степенного ряда
mpreal get_delta_t(mpreal &alpha0, mpreal &beta0, mpreal &gamma0)
{
mpreal h2 = (mpfr::max)((mpfr::max)(fabs(alpha0), fabs(beta0)), fabs(gamma0)),
h1 = (mpfr::max)((mpfr::max)(2*sigma, r+2*h2+1), b+2*h2+1);
mpreal h3 = h2 >= 1 ? h1 * h2 : (mpfr::max)((mpfr::max)(2*sigma, r+2), b+1);
return 1/(h3 + "1e-10");
}
// Функция экспериментального определения машинного эпсилон
void machine_eps()
{
mpreal e, e1;
int k = 0;
e = 1;
do
{
e /= 2;
e1 = e+1;
k++;
}
while (e1 > 1);
cout << "Число делений на 2 = " << k << endl;
cout << "Машинный эпсилон = " << e << endl;
}
// Функция вычисления значений фазовых координат в конечный момент времени
// x, y и z - координаты начальной точки; T - длина отрезка интегрирования;
// way - направление поиска решений: 1 - вперед по времени, -1 - назад по времени
void calc(mpreal &x, mpreal &y, mpreal &z, mpreal T, int way = 1)
{
cout << "\nВ начальный момент времени:\n\ndx/dt = " << sigma*(y-x) << "\ndy/dt = " << r*x-y-x*z <<
"\ndz/dt = " << x*y-b*z << endl;
mpreal t = 0;
mpreal delta_t;
while (t <= T)
{
if(FL_CALC)
delta_t = get_delta_t(x, y, z);
else
delta_t = step_t;
t += delta_t;
vector<mpreal> alpha, beta, gamma;
alpha.push_back(x);
beta.push_back(y);
gamma.push_back(z);
int i = 0;
mpreal L = sqrt(alpha[0]*alpha[0] + beta[0]*beta[0] +
gamma[0]*gamma[0]);
mpreal p = way * delta_t;
while(L > eps_c)
{
// Вычисляем новые коэффициенты степенных рядов
mpreal s1 = 0, s2 = 0;
for(int j = 0; j <= i; j++)
{
s1 += alpha[j] * gamma[i-j];
s2 += alpha[j] * beta[i-j];
}
alpha.push_back(sigma*(beta[i] - alpha[i])/(i+1));
beta.push_back((r*alpha[i] - beta[i] - s1)/(i+1));
gamma.push_back((s2 - b*gamma[i])/(i+1));
i++;
x += alpha[i] * p;
y += beta[i] * p;
z += gamma[i] * p;
L = fabs(p) * sqrt(alpha[i]*alpha[i] + beta[i]*beta[i] +
gamma[i]*gamma[i]);
p *= way * delta_t;
}
}
cout << "\nКоординаты в конечный момент времени:\nx = " << x.toString(-1) << "\ny = " << y.toString(-1) <<
"\nz = " << z.toString(-1) << endl;
cout << "\nЗначения производных:\n\ndx/dt = " << sigma*(y-x) << "\ndy/dt = " << r*x-y-x*z << "\ndz/dt = " << x*y-b*z << endl;
}
int main()
{
mpreal::set_default_prec(prec);
mpreal::set_emin(-1024);
mpreal::set_emax(1024);
machine_eps();
mpreal T;
cout << "\nВведите длину отрезка времени > ";
cin >> T;
mpreal x, y, z;
cout << "\nx0 > ";
cin >> x;
cout << "y0 > ";
cin >> y;
cout << "z0 > ";
cin >> z;
cout << endl;
calc(x, y, z, T);
cout << "\n\n*** Проход назад ***\n";
calc(x, y, z, T, -1);
return 0;
}
Для компиляции файла lorenz.cpp с этим кодом выполним следующее
g++ lorenz.cpp -lmpfr -lgmp -o lorenz
Как видно из листинга программы, для хранения значений коэффициентов степенных рядов используются векторы из библиотеки STL. Было принято, что количество бит под мантиссу вещественного числа равно 180. Диапазон изменения экспоненты — от -1024 до 1024. Функция экспериментального определения машинного эпсилон

была использована для того, чтобы проверить его значение для заданного представления вещественного числа. В данном случае

Приведем результаты вычислительного эксперимента. В качестве начальных условий возьмем значения, близкие к аттрактору Лоренца:

Отрезок времени, на котором производилось вычисления, —

. Первоначально точность оценки общего члена ряда бралась равной

. Этого достаточно, чтобы получить результат

значения производных

(уменьшая значение

, результат не изменится). При этом можно брать вещественные числа с меньшим объемом памяти.
Значения производных, как и значения координат, приведены для того, чтобы проиллюстрировать факт возвращения траектории в окрестность начальной точки, но незамыкания, как это следовало бы ожидать из гипотезы существования циклов в системе (1). После такого сближения точка траектории уходит от своего начального положения, но потом опять возвращается в ее окрестность. Такое поведение предсказывает качественная теория дифференциальных уравнений (устойчивость по Пуассону точек рекуррентных траекторий на аттракторе; это было указано в [1] и обсуждено на конференции [4]).
Указанная разрядность для вещественного числа была выбрана с целью отследить не только возврат траектории системы Лоренца в окрестность начальных условий [1, рис. 1], но и для прохода назад по времени от конечной точки к начальной по дуге траектории (равенство параметра way функции calc() -1). Тогда в расчетах нужно брать

. В результате получаются значения, совпадающие с начальными до четвертого знака после запятой (-1, переданная в качестве параметра методу toString() класса mpreal, говорит о преобразовании числа в строку с максимальным количеством знаков после запятой):
x = 13.4126562226118907078771507151144392594947158244822557
y = 13.4643106138333931236007875084005714993319786943366669
z = 33.4615530132812572274810796387886946762995539968650496
Такое малое значение
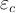
выбрано потому, что при движении по траектории в отрицательные значения времени наблюдается сильная неустойчивость решений — они сразу уходят в бесконечность от аттрактора, поскольку мы при расчетах находимся вблизи от него, а не непосредственно на нем.
В программе также предусмотрено фиксированное значение шага. Проверено, число 0.02 может быть использовано для построений приближенных решений вблизи аттрактора Лоренца. Это значение гораздо больше того, которое получается из приведенной оценки из работы [2] (флаг FL_CALC равен 1) для любых начальных условий, но при удалении начальной точки на значительное расстояние от притягивающего множества метод перестает работать (ряды не сходятся).
В работе [5, с. 90, 91] для исследования траекторий системы (1) применяется метод Эйлера с переменным шагом

интегрирования. Величина

выбирается с отслеживанием ошибки на текущем шаге (т.е. локальный контроль), используя интервальную арифметику. Однако нет проверки общей ошибки интегрирования. Проход назад по времени, описанный выше, нам гарантирует правильность построения приближенного решения. Варьируя точностью оценки общего члена ряда, можно уменьшить ошибку на шаге, что не позволяет метод Эйлера. Также в рассмотренной модификации метода степенных рядов преимуществом перед общей схемой метода рядов Тейлора является быстрый расчет по формулам (3) коэффициентов разложения по сравнению с процедурой символьного дифференцирования правых частей уравнений системы (кроме того, в нелинейном случае под символьные выражения требуется много памяти для их хранения при вычислении производных высших порядков).
Таким образом, зная состояние системы Лоренца в прошлом, мы с достаточной степенью точности можем предсказать поведение ее траекторий в течение длительных интервалов времени, а также вернуться назад. По сути здесь нарушается формальное определение хаоса [6, с. 118, 119].
Литература
1. Пчелинцев А.Н. Критический взгляд на аттрактор Лоренца, 2013.
Хабрахабр.
2. Pchelintsev A.N. Numerical and physical modeling of the dynamics of the Lorenz system // Numerical Analysis and Applications, 7(2): 159-167, 2014. DOI:
10.1134/S1995423914020098.
3. Магницкий Н.А., Сидоров С.В. Новые методы хаотической динамики. — М.: Едиториал УРСС, 2004.
4. Пчелинцев А.Н. О моделировании динамики системы Лоренца // Международная конференция «Колмогоровские чтения VI. Общие проблемы управления и их приложения (ОПУ-2013)», Тамбовский государственный университет им. Г.Р. Державина (Тамбов, 2013 год).
Math-Net.Ru.
5. Tucker W. A
Rigorous ODE Solver and Smale's 14th Problem // Foundations of Computational Mathematics, 2(1): 53-117, 2002.
6. Берже П., Помо И., Видаль К. Порядок в хаосе. О детерминистком подходе к турбулентности. — М.: Мир, 1991.


 , r и b являются положительными числами. Для исследования поведения решений системы обычно берут классические значения параметров системы, т.е.
, r и b являются положительными числами. Для исследования поведения решений системы обычно берут классические значения параметров системы, т.е.
 интегрирования и точности представления вещественного числа для управления вычислительным процессом), во-вторых, большой объем вычислений при очень малых
интегрирования и точности представления вещественного числа для управления вычислительным процессом), во-вторых, большой объем вычислений при очень малых  .
.

 ,
,  и
и  определяются начальными условиями; также получена длина (шаг)
определяются начальными условиями; также получена длина (шаг)  отрезка сходимости рядов (2):
отрезка сходимости рядов (2):
 , то
, то  , иначе
, иначе  ,
, — любое положительное число.
— любое положительное число. ,
,  и
и  до такого значения i, при котором имеет место оценка для заданной точности
до такого значения i, при котором имеет место оценка для заданной точности 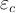 вычислений
вычислений
 была использована для того, чтобы проверить его значение для заданного представления вещественного числа. В данном случае
была использована для того, чтобы проверить его значение для заданного представления вещественного числа. В данном случае

 . Первоначально точность оценки общего члена ряда бралась равной
. Первоначально точность оценки общего члена ряда бралась равной  . Этого достаточно, чтобы получить результат
. Этого достаточно, чтобы получить результат

 , результат не изменится). При этом можно брать вещественные числа с меньшим объемом памяти.
, результат не изменится). При этом можно брать вещественные числа с меньшим объемом памяти. . В результате получаются значения, совпадающие с начальными до четвертого знака после запятой (-1, переданная в качестве параметра методу toString() класса mpreal, говорит о преобразовании числа в строку с максимальным количеством знаков после запятой):
. В результате получаются значения, совпадающие с начальными до четвертого знака после запятой (-1, переданная в качестве параметра методу toString() класса mpreal, говорит о преобразовании числа в строку с максимальным количеством знаков после запятой):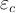 выбрано потому, что при движении по траектории в отрицательные значения времени наблюдается сильная неустойчивость решений — они сразу уходят в бесконечность от аттрактора, поскольку мы при расчетах находимся вблизи от него, а не непосредственно на нем.
выбрано потому, что при движении по траектории в отрицательные значения времени наблюдается сильная неустойчивость решений — они сразу уходят в бесконечность от аттрактора, поскольку мы при расчетах находимся вблизи от него, а не непосредственно на нем. интегрирования. Величина
интегрирования. Величина  выбирается с отслеживанием ошибки на текущем шаге (т.е. локальный контроль), используя интервальную арифметику. Однако нет проверки общей ошибки интегрирования. Проход назад по времени, описанный выше, нам гарантирует правильность построения приближенного решения. Варьируя точностью оценки общего члена ряда, можно уменьшить ошибку на шаге, что не позволяет метод Эйлера. Также в рассмотренной модификации метода степенных рядов преимуществом перед общей схемой метода рядов Тейлора является быстрый расчет по формулам (3) коэффициентов разложения по сравнению с процедурой символьного дифференцирования правых частей уравнений системы (кроме того, в нелинейном случае под символьные выражения требуется много памяти для их хранения при вычислении производных высших порядков).
выбирается с отслеживанием ошибки на текущем шаге (т.е. локальный контроль), используя интервальную арифметику. Однако нет проверки общей ошибки интегрирования. Проход назад по времени, описанный выше, нам гарантирует правильность построения приближенного решения. Варьируя точностью оценки общего члена ряда, можно уменьшить ошибку на шаге, что не позволяет метод Эйлера. Также в рассмотренной модификации метода степенных рядов преимуществом перед общей схемой метода рядов Тейлора является быстрый расчет по формулам (3) коэффициентов разложения по сравнению с процедурой символьного дифференцирования правых частей уравнений системы (кроме того, в нелинейном случае под символьные выражения требуется много памяти для их хранения при вычислении производных высших порядков).